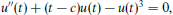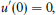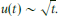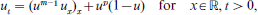In a recent paper devoted to the study of the superheating field attached to a semi-infinite superconductor, Chapman [1] constructs a family of approximate solutions of the Ginzburg–Landau system. This construction, based on a matching procedure, implicitly uses the existence of a family of solutions depending on a parameter c∈IR of the Painlevé equation in a semi-infinite interval (0, +∞)

with a Neumann condition at 0

and having a prescribed behaviour at +∞

In this paper we prove the existence of such a family of solutions and investigate its properties. Moreover, we prove that the second coefficient in Chapman's expansion of the superheating field is finite.

We show how to find all the integrating factors and corresponding first integrals for any system of Ordinary Differential Equations (ODEs). Integrating factors are shown to be all solutions of both the adjoint system of the linearised system of ordinary differential equations and a system that represents an extra adjoint-invariance condition. We present an explicit construction formula to find the resulting first integrals in terms of integrating factors, and discuss techniques for finding integrating factors. In particular, we show how to utilize known first integrals and symmetries to find new integrating factors. Illustrative examples are given.

In this paper we consider a non-local anisotropic model for phase separation in two-phase fluids at equilibrium, and show that when the thickness of the interface tends to zero in a suitable way, the classical surface tension model is recovered. Relevant examples are given by continuum limits of ferromagnetic Ising systems in equilibrium statistical mechanics.

We study the propagation properties of the reaction-diffusion equation of Fisher type

with p<1<m. Taking into account that solutions of the Cauchy problem are nonunique if m+p⩾2, we prove that the minimal solutions in this case tend to propagate with certain minimal speed c∗(m, p). More precisely, if we translate any solution with a velocity ∣c∣<c∗, we get the limit in time value one, and if the initial value u(·, 0) vanishes, say, for x⩾0, the minimal solution translated with velocity c>c∗ tends to zero. Also, an interface appears for the minimal solutions, whose asymptotic velocity is c∗. This behaviour depends upon the existence of special solutions of travelling wave form. Travelling waves have been widely studied for diffusion equations related with the above. We characterize here the minimal velocity c∗ for which travelling waves exist, as an analytic function of the parameters m and p, for every m+p⩾2, by viewing it as an anomalous exponent. Some local properties of the minimal solutions and their interfaces in the case m+p⩾2 are also proved.

The behaviour of adhesively bonded joints is investigated using a continuum mechanical description for the adhesive. The gradient of the adhesion variable, which describes the volumetric proportion of cavities within the adhesive, is introduced in the free energy, so that the model accounts for the intrinsic cohesion of the adhesive. The adherends are linear elastic materials and the adhesive is first given an elastic behaviour. Using a thermodynamical framework, an adhesion potential function is established, the subdifferential of which is determined in a rigorous way, so that three-dimensional coupled elastic-adhesion evolution equations are derived. Then we consider a generalization to the coupling of adhesion with elastoplasticity. A two-dimensional model of adhesive bonding is derived using a perturbation method. Finally, a finite element discretization of the coupled evolution problem is presented and a resolution scheme based on Newton's method is developed, while the integration of the constitutive law is performed using a three-step operator splitting method.

The one-dimensional porous medium equation ht= (hmhx)x (m>0) admits waiting-time solutions, whose front remains motionless during a finite time interval tw before starting to move. We consider a family of initial value problems, and investigate the asymptotics, close to the front and near start-up, which we expect to be self-similar. We obtain numerical solutions for viscous gravity currents (m=3) and power-law initial conditions (h∝xp, h is proportional to the thickness of the fluid, x is the distance to the front). We find that: (a) if p<2/3 the front starts moving immediately, (b) if p=2/3 the front remains motionless during a finite time, (c) if p>2/3 one obtains waiting-time solutions in which a moving corner layer (a small interval Δx in which hx varies strongly) appears behind the front; the front starts moving when it is overrun by the corner layer. The corner layer strengthens (Δx reduces and the variation of hx increases) as it approaches the front. Our initial conditions produce waiting-time solutions whose front starts moving with nonzero velocity. We determine tw(p) and study the motion of the corner layer and the front, as well as other properties of the solutions. We compare the results with the theoretical upper and lower bounds of tw. We investigate the asymptotics of the numerical solutions for p>2/3, close to the corner layer and the front, and near start-up. To represent this asymptotics various kinds of similarity solutions are available, that can be classified according to the self-similarity exponent δ. We find that only two types (called L and A) are relevant. The L solutions correspond to 1<δ<13/10, and have an infinite series of corner layers that accumulate at the front. The part of these solutions behind the first corner layer of the series represents the asymptotics of the numerical solutions in a domain that excludes the region between the corner layer and the front, for a time interval excluding the neighbourhood of start-up. The A solutions have δ⩽1, and represent the evolution of the strong corner layer that is arriving at the front. The numerical evidence shows that the constant front velocity solution (type A with δ=1) describes the asymptotics close to, and including start-up, so that the motion of the corner layer joins smoothly with that of the front.