Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T17:02:40.700Z Has data issue: false hasContentIssue false
  • English
  • Français

Lp-theory for the stochastic heat equationwith infinite-dimensional fractional noise*

Published online by Cambridge University Press:  05 January 2012

Raluca M. Balan
Raluca M. Balan*
Affiliation:
University of Ottawa, Department of Mathematics and Statistics, 585 King Edward Avenue Ottawa, ON, K1N 6N5, Canada; [email protected], http://aix1.uottawa.ca/~rbalan
Get access

Abstract

In this article, we consider the stochastic heat equation $du=(\Delta u+f(t,x)){\rm d}t+ \sum_{k=1}^{\infty} g^{k}(t,x) \delta \beta_t^k, t \in [0,T]$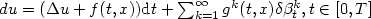, with random coefficients f and gk,driven by a sequence (βk)k of i.i.d. fractional Brownianmotions of index H>1/2. Using the Malliavin calculus techniquesand a p-th moment maximal inequality for the infinite sum ofSkorohod integrals with respect to (βk)k, we prove that theequation has a unique solution (in a Banach space of summabilityexponent p ≥ 2), and this solution is Hölder continuous inboth time and space.

Keywords

Fractional Brownian motionSkorohod integralmaximal inequalitystochastic heat equation
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 15: Supplement: In honor of Marc Yor , 2011 , pp. 110 - 138
Copyright
© EDP Sciences, SMAI, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alòs, E., Mazet, O. and Nualart, D., Stochastic calculus with respect to Gaussian processes. Ann. Probab. 29 (2001) 766–801.
Alòs, E. and Nualart, D., Stochastic integration with respect to the fractional Brownian motion. Stoch. Stoch. Rep. 75 (2003) 129–152. CrossRef
Balan, R.M. and Tudor, C.A., The stochastic heat equation with a fractional-colored noise: existence of the solution. Latin Amer. J. Probab. Math. Stat. 4 (2008) 57–87.
P. Carmona and L. Coutin, Stochastic integration with respect to fractional Brownian motion. Ann. Inst. Poincaré, Probab. & Stat. 39 (2003) 27–68.
G. Da Prato and J. Zabczyk, Stochastic Equations in Infinite Dimensions. Cambridge University Press (1992).
Decreusefond, L. and Ustünel, A.S., Stochastic analysis of the fractional Brownian motion. Potent. Anal. 10 (1999) 177–214. CrossRef
Duncan, T.E., Hu, Y. and Pasik-Duncan, B., Stochstic calculus for fractional Brownian motion I. theory. SIAM J. Contr. Optim. 38 (2000) 582–612. CrossRef
Grecksch, W. and Anh, V.V., A parabolic stochastic differential equation with fractional Brownian motion input. Stat. Probab. Lett. 41 (1999) 337–346. CrossRef
Y. Hu, Integral transformations and anticipative calculus for fractional Brownian motions. Memoirs AMS 175 (2005) viii+127.
G. Kallianpur and J. Xiong, Stochastic Differential Equations in Infinite Dimensional Spaces. IMS Lect. Notes 26, Hayward, CA (1995).
Krylov, N.V., A generalization of the Littlewood-Paley inequality and some other results related to stochstic partial differential equations. Ulam Quarterly 2 (1994) 16–26.
Krylov, N.V., On L p-theory of stochastic partial differential equations in the whole space. SIAM J. Math. Anal. 27 (1996) 313–340 CrossRef
Krylov, N.V., An analytic approach to SPDEs. In Stochastic partial differential equations: six perspectives. Math. Surveys Monogr. 64 (1999) 185–242 AMS, Providence, RI. CrossRef
N.V. Krylov, On the foundation of the L p-theory of stochastic partial differential equations. In “Stochastic partial differential equations and application VII”. Chapman & Hall, CRC (2006) 179–191.
Lyons, T., Differential equations driven by rough signals. Rev. Mat. Iberoamericana 14 (1998) 215–310. CrossRef
T. Lyons and Z. Qian, System Control and Rough Paths. Oxford University Press (2002).
Maslowski, B. and Nualart, D., Evolution equations driven by a fractional Brownian motion. J. Funct. Anal. 202 (2003) 277–305. CrossRef
Nualart, D., Analysis on Wiener space and anticipative stochastic calculus. Lect. Notes. Math. 1690 (1998) 123–227. CrossRef
Nualart, D., Stochastic integration with respect to fractional Brownian motion and applications. Contem. Math. 336 (2003) 3–39. CrossRef
D. Nualart, Malliavin Calculus and Related Topics, Second Edition. Springer-Verlag, Berlin.
Nualart, D. and Vuillermot, P.-A., Variational solutions for partial differential equations driven by fractional a noise. J. Funct. Anal. 232 (2006) 390–454. CrossRef
B.L. Rozovskii, Stochastic evolution systems. Kluwer, Dordrecht (1990).
M. Sanz-Solé and P.-A. Vuillermot, Mild solutions for a class of fractional SPDE's and their sample paths (2007). Preprint available at http://www.arxiv.org/pdf/0710.5485
E.M. Stein, Singular Integrals and Differentiability Properties of Functions. Princeton University Press, Princeton (1970).
Tindel, S., Tudor, C.A., and Viens, F., Stochastic evolution equations with fractional Brownian motion. Probab. Th. Rel. Fields 127 (2003) 186–204. CrossRef
Walsh, J.B., An introduction to stochastic partial differential equations. École d'Été de Probabilités de Saint-Flour XIV. Lecture Notes in Math. 1180 (1986) 265–439. Springer, Berlin. CrossRef
Zähle, M., Integration with respect to fractal functions and stochastic calculus I. Probab. Th. Rel. Fields 111 (1998) 333–374.