Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Callegaro, Giorgia
2013.
Optimal consumption problems in discontinuous markets.
Optimization,
Vol. 62,
Issue. 11,
p.
1575.
Kchia, Younes
Larsson, Martin
and
Protter, Philip
2013.
Malliavin Calculus and Stochastic Analysis.
Vol. 34,
Issue. ,
p.
469.
Ellanskaya, A.
and
Vostrikova, L.
2014.
Utility maximisation and utility indifference price for exponential semi-martingale models and HARA utilities.
Proceedings of the Steklov Institute of Mathematics,
Vol. 287,
Issue. 1,
p.
68.
Tian, Kun
Xiong, Dewen
and
Ye, Zhongxing
2014.
The Dynamic Spread of the Forward CDS with General Random Loss.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
Fontana, Claudio
Grbac, Zorana
Jeanblanc, Monique
and
Li, Qinghua
2014.
Information, no-arbitrage and completeness for asset price models with a change point.
Stochastic Processes and their Applications,
Vol. 124,
Issue. 9,
p.
3009.
JEANBLANC, MONIQUE
and
LENIEC, MARTA
2015.
ROLE OF INFORMATION IN PRICING DEFAULT-SENSITIVE CONTINGENT CLAIMS.
International Journal of Theoretical and Applied Finance,
Vol. 18,
Issue. 01,
p.
1550007.
Jeanblanc, Monique
and
Song, Shiqi
2015.
Martingale representation property in progressively enlarged filtrations.
Stochastic Processes and their Applications,
Vol. 125,
Issue. 11,
p.
4242.
Song, Shiqi
2016.
Drift operator in a viable expansion of information flow.
Stochastic Processes and their Applications,
Vol. 126,
Issue. 8,
p.
2297.
Callegaro, Giorgia
Gaïgi, M’hamed
Scotti, Simone
and
Sgarra, Carlo
2017.
Optimal investment in markets with over and under-reaction to information.
Mathematics and Financial Economics,
Vol. 11,
Issue. 3,
p.
299.
El Karoui, Nicole
Jeanblanc, Monique
and
Jiao, Ying
2017.
Dynamics of multivariate default system in random environment.
Stochastic Processes and their Applications,
Vol. 127,
Issue. 12,
p.
3943.
Janke, Oliver
2017.
Utility maximization under risk constraints and incomplete information for a market with a change point.
Applied Mathematical Finance,
Vol. 24,
Issue. 5,
p.
451.
Jeanblanc, Monique
Li, Libo
and
Song, Shiqi
2018.
An enlargement of filtration formula with applications to multiple non-ordered default times.
Finance and Stochastics,
Vol. 22,
Issue. 1,
p.
205.
Jiao, Ying
and
Kharroubi, Idris
2018.
Information uncertainty related to marked random times and optimal investment.
Probability, Uncertainty and Quantitative Risk,
Vol. 3,
Issue. 1,
Esmaeeli, Neda
and
Imkeller, Peter
2018.
American options with asymmetric information and reflected BSDE.
Bernoulli,
Vol. 24,
Issue. 2,
Fontana, Claudio
2018.
The strong predictable representation property in initially enlarged filtrations under the density hypothesis.
Stochastic Processes and their Applications,
Vol. 128,
Issue. 3,
p.
1007.
Calzolari, Antonella
and
Torti, Barbara
2019.
Martingale representations in progressive enlargement by the reference filtration of a semi-martingale: a note on the multidimensional case.
Stochastics,
Vol. 91,
Issue. 2,
p.
265.
Calzolari, Antonella
and
Torti, Barbara
2019.
Frontiers in Stochastic Analysis–BSDEs, SPDEs and their Applications.
Vol. 289,
Issue. ,
p.
109.
Aksamit, Anna
Jeanblanc, Monique
and
Rutkowski, Marek
2019.
Integral representations of martingales for progressive enlargements of filtrations.
Stochastic Processes and their Applications,
Vol. 129,
Issue. 4,
p.
1229.
Esmaeeli, N.
Imkeller, P.
and
Nzengang, V.
2019.
Dynkin Game with Asymmetric Information.
Bulletin of the Iranian Mathematical Society,
Vol. 45,
Issue. 1,
p.
283.
Calvia, Alessandro
and
Gianin, Emanuela Rosazza
2020.
Risk Measures and Progressive Enlargement of Filtration: A BSDE Approach.
SIAM Journal on Financial Mathematics,
Vol. 11,
Issue. 3,
p.
815.
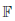 F with a random time τ. We provide, under anequivalence assumption, slightly stronger than the absolute continuity assumption ofJacod, alternative proofs to results concerning canonical decomposition of an \hbox{$\mathbb{F}$}
F with a random time τ. We provide, under anequivalence assumption, slightly stronger than the absolute continuity assumption ofJacod, alternative proofs to results concerning canonical decomposition of an \hbox{$\mathbb{F}$}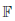 F-martingalein the enlarged filtrations. Also, we address martingales’ characterization in theenlarged filtrations in terms of martingales in the reference filtration, as well aspredictable representation theorems in the enlarged filtrations.
F-martingalein the enlarged filtrations. Also, we address martingales’ characterization in theenlarged filtrations in terms of martingales in the reference filtration, as well aspredictable representation theorems in the enlarged filtrations.