Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T04:38:05.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical solution of parabolic equationsin high dimensions

Published online by Cambridge University Press:  15 February 2004

Tobias von Petersdorff  and
Christoph Schwab
Tobias von Petersdorff
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, USA.
Christoph Schwab
Affiliation:
Seminar for Applied Mathematics, ETH Zentrum, 8092 Zürich, Switzerland. [email protected].
Get access

Abstract

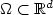We consider the numerical solution of diffusion problems in (0,T) x Ω for $\Omega\subset \mathbb{R}^d$ and for T > 0 indimension dd ≥ 1. We use a wavelet based sparse gridspace discretization with mesh-width h and order pd ≥ 1, andhp discontinuous Galerkin time-discretization of order $r =O(\left|\log h\right|)$ 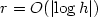on a geometric sequence of $O(\left|\log h\right|)$ 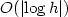many timesteps. The linear systems in each time step are solved iterativelyby $O(\left|\log h\right|)$ 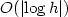GMRES iterations with a wavelet preconditioner. We prove that this algorithm gives an L 2(Ω)-error of O(N-p) for u(x,T) where N is the total number of operations,provided that the initial data satisfies $u_0 \in H^\varepsilon(\Omega)$ 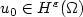with ε > 0 and that u(x,t) is smooth in x for t>0. Numerical experiments in dimension d up to 25 confirm thetheory.

Keywords

Discontinuous Galerkin methodsparse gridwavelets.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 38 , Issue 1 , January 2004 , pp. 93 - 127
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

H. Amann, Linear and Quasilinear Parabolic Problems 1: Abstract Linear Theory. Birkhäuser, Basel (1995).
Bungartz, H.-J. and Griebel, M., A note on the complexity of solving Poisson's equation for spaces of bounded mixed derivatives. J. Complexity 15 (1999) 167–199. CrossRef
Eisenstat, S.C., Elman, H.C. and Schultz, M.H., Variational iterative methods for nonsymmetric systems of linear equations. SIAM J. Numer. Anal. 20 (1983) 345–357. CrossRef
Griebel, M. and Knapek, S., Optimized tensor product approximation spaces. Constr. Approx. 16 (2000) 525–540. CrossRef
Griebel, M., Oswald, P. and Schiekofer, T., Sparse grids for boundary integral equations. Numer. Math. 83 (1999) 279–312. CrossRef
J.L. Lions and E. Magenes, Non-homogeneous boundary value problems and applications I. Springer-Verlag (1972).
P. Oswald, On best N-term approximation by Haar functions in Hs -norms, in Metric Function Theory and Related Topics in Analysis. S.M. Nikolskij, B.S. Kashin, A.D. Izaak Eds., AFC, Moscow (1999) 137–163 (in Russian).
H.C. Öttinger, Stochastic Processes in polymeric fluids. Springer-Verlag (1998).
A. Pazy, Semigroups of Linear Operators and Applications to Partial Differential Equations. Appl. Math. Sci., Springer-Verlag, New York 44 (1983).
Schmidlin, G., Lage, C. and Schwab, C., Rapid solution of first kind boundary integral equations in $\mathbb{R}^3$ . Eng. Anal. Bound. Elem. 27 (2003) 469–490. CrossRef
D. Schötzau, hp-DGFEM for Parabolic Evolution Problems. Dissertation ETH Zurich (1999).
Schötzau, D. and Schwab, C., Time discretization of parabolic problems by the hp-version of the discontinuous Galerkin finite element method. SIAM J. Numer. Analysis 38 (2000) 837–875. CrossRef
Schötzau, D. and Schwab, C., hp-Discontinuous Galerkin time-stepping for parabolic problems. C.R. Acad. Sci. Paris 333 (2001) 1121–1126. CrossRef
C. Schwab, p and hp Finite Element Methods. Oxford University Press (1998).
C. Schwab and R.A. Todor, Sparse finite elements for stochastic elliptic problems-higher order moments (in press in Computing 2003), http://www.math.ethz.ch/research/groups/sam/reports/2003
V. Thomee, Galerkin Finite Element Methods for Parabolic Problems. Springer-Verlag (1997).
von Petersdorff, T. and Schwab, C., Wavelet-discretizations of parabolic integro-differential equations. SIAM J. Numer. Anal. 41 (2003) 159–180. CrossRef
Werder, T., Schötzau, D., Gerdes, K. and Schwab, C., hp-Discontinuous Galerkin time-stepping for parabolic problems. Comput. Methods Appl. Mech. Eng. 190 (2001) 6685–6708. CrossRef