No CrossRef data available.
Article contents
Characterization of the limit load in the case of an unbounded elastic convex
Published online by Cambridge University Press: 15 August 2005
Abstract
In this work we consider a solid body $\Omega\subset{\Bbb R}^3$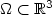 constituted by a
nonhomogeneous elastoplastic material, submitted to a density of body forces $\lambda f $
constituted by a
nonhomogeneous elastoplastic material, submitted to a density of body forces $\lambda f $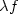 and a density of forces $\lambda g$
and a density of forces $\lambda g$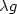 acting on the boundary where the real $\lambda $
acting on the boundary where the real $\lambda $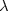 is the
loading parameter.
The problem is to determine, in the case of an unbounded convex of elasticity, the Limit
load denoted by $\bar{\lambda}$
is the
loading parameter.
The problem is to determine, in the case of an unbounded convex of elasticity, the Limit
load denoted by $\bar{\lambda}$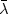 beyond which there is a break of the structure. The case of a bounded convex of elasticity is done in [El-Fekih and Hadhri, RAIRO: Modél. Math. Anal. Numér. 29 (1995) 391–419].
Then assuming that the convex of elasticity at the point x of Ω, denoted
by K(x), is written in the form of $\mbox{K}^D (x) + {\Bbb
R}\mbox{I}$
beyond which there is a break of the structure. The case of a bounded convex of elasticity is done in [El-Fekih and Hadhri, RAIRO: Modél. Math. Anal. Numér. 29 (1995) 391–419].
Then assuming that the convex of elasticity at the point x of Ω, denoted
by K(x), is written in the form of $\mbox{K}^D (x) + {\Bbb
R}\mbox{I}$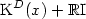 , I is the identity of ${{\Bbb R}^9}_{sym}$
, I is the identity of ${{\Bbb R}^9}_{sym}$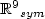 , and the
deviatoric component $\mbox{K}^D$
, and the
deviatoric component $\mbox{K}^D$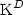 is bounded regardless of x
$\in\Omega$
is bounded regardless of x
$\in\Omega$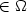 , we show under the condition “Rot f $\not= 0$
, we show under the condition “Rot f $\not= 0$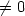 or g is not colinear to the normal on a part of the boundary of Ω", that the
Limit Load $\bar{\lambda}$
or g is not colinear to the normal on a part of the boundary of Ω", that the
Limit Load $\bar{\lambda}$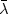 searched is equal to the inverse of
the infimum of the gauge of the Elastic convex translated by
stress field equilibrating the unitary load corresponding to
$\lambda =1$
searched is equal to the inverse of
the infimum of the gauge of the Elastic convex translated by
stress field equilibrating the unitary load corresponding to
$\lambda =1$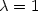 ; moreover we show that this infimum is reached in a
suitable function space.
; moreover we show that this infimum is reached in a
suitable function space.
Keywords
- Type
- Research Article
- Information
- ESAIM: Mathematical Modelling and Numerical Analysis , Volume 39 , Issue 4 , July 2005 , pp. 637 - 648
- Copyright
- © EDP Sciences, SMAI, 2005


