Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T15:22:15.105Z Has data issue: false hasContentIssue false
  • English
  • Français

A posteriori error analysis for parabolicvariational inequalities

Published online by Cambridge University Press:  02 August 2007

Kyoung-Sook Moon ,
Ricardo H. Nochetto ,
Tobias von Petersdorff  and
Chen-song Zhang
Kyoung-Sook Moon
Affiliation:
Department of Mathematics and Information, Kyungwon University, Bokjeong-dong, Sujeong-gu, Seongnam-si, Gyeonggi-do, 461-701, Korea. [email protected]
Ricardo H. Nochetto
Affiliation:
Department of Mathematics and Institute for Physical Science and Technology, University of Maryland, College Park, MD 20742, USA. [email protected]
Tobias von Petersdorff
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, USA. [email protected]; [email protected]
Chen-song Zhang
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, USA. [email protected]; [email protected]
Get access

Abstract

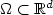Motivated by the pricing of American options for baskets weconsider a parabolic variational inequality in a boundedpolyhedral domain $\Omega\subset\mathbb{R}^d$ with a continuous piecewisesmooth obstacle. We formulate a fully discrete method by usingpiecewise linear finite elements in space and the backward Eulermethod in time. We define an a posteriori error estimator and showthat it gives an upper bound for the error inL2(0,T;H1 (Ω)). The error estimator is localized in thesense that the size of the elliptic residual is only relevant inthe approximate non-contact region, and the approximability of theobstacle is only relevant in the approximate contact region. Wealso obtain lower bound results for the space error indicators inthe non-contact region, and for the time error estimator.Numerical results for d=1,2 show that the error estimator decayswith the same rate as the actual error when the space meshsize hand the time step τ tend to zero. Also, the error indicatorscapture the correct behavior of the errors in both the contact andthe non-contact regions.

Keywords

A posteriori error analysisfinite element methodvariational inequalityAmerican option pricing.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 41 , Issue 3 , May 2007 , pp. 485 - 511
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

W. Bangerth and R. Rannacher, Adaptive Finite Element Methods for Differential Equations. Lectures in Mathematics ETH Zürich, Birkhäuser Verlag (2003).
Bergam, A., Bernardi, C. and Mghazli, Z., A posteriori analysis of the finite element discretization of some parabolic equations. Math. Comp. 74 (2005) 1117–1138 (electronic). CrossRef
Black, F. and Scholes, M., The pricing of options and corporate liabilities. J. Polit. Econ. 81 (1973) 637–659. CrossRef
H. Brézis, Opérateurs maximaux monotones et semi-groupes de contraction dans les espaces de Hilbert. North Holland (1973).
Brézis, H. and Browder, F.E., Nonlinear integral equations and systems of Hammerstein type. Adv. Math. 18 (1975) 115–147. CrossRef
M. Broadie and J. Detemple, Recent advances in numerical methods for pricing derivative securities, in Numerical Methods in Finance, L.C.G. Rogers and D. Talay Eds., Cambridge University Press (1997) 43–66.
Caffarelli, L.A., The regularity of monotone maps of finite compression. Comm. Pure Appl. Math. 50 (1997) 563–591. 3.0.CO;2-6>CrossRef
Chen, Z. and Nochetto, R.H., Residual type a posteriori error estimates for elliptic obstacle problems. Numer. Math. 84 (2000) 527–548. CrossRef
C.W. Cryer, Successive overrelaxation methods for solving linear complementarity problems arising from free boundary problems, Free boundary problems I, Ist. Naz. Alta Mat. Francesco Severi (1980) 109–131.
Fetter, A., L ∞-error estimate for an approximation of a parabolic variational inequality. Numer. Math. 50 (1987) 57–565. CrossRef
Fierro, F. and Veeser, A., A posteriori error estimators for regularized total variation of characteristic functions. SIAM J. Numer. Anal. 41 (2003) 2032–2055. CrossRef
R. Glowinski, Numerical methods for nonlinear variational problems. Springer series in computational physics, Springer-Verlag (1984).
Jaillet, P., Lamberton, D. and Lapeyre, B., Variational inequalities and the pricing of American options. Acta Appl. Math. 21 (1990) 263–289. CrossRef
Johnson, C., Convergence estimate for an approximation of a parabolic variational inequatlity. SIAM J. Numer. Anal. 13 (1976) 599–606. CrossRef
D. Lamberton and B. Lapeyre, Introduction to stochastic calculus applied to finance. Springer (1996).
R.H. Nochetto and C.-S. Zhang, Adaptive mesh refinement for evolution obstacle problems (in preparation).
Nochetto, R.H., Savaré, G. and Verdi, C., Error control for nonlinear evolution equations. C.R. Acad. Sci. Paris Ser. I 326 (1998) 1437–1442. CrossRef
R.H. Nochetto, G. Savaré and C. Verdi, A posteriori error estimates for variable time-step discretizations of nonlinear evolution equations. Comm. Pure Appl. Math. 53 (2000) 525–589.
Nochetto, R.H., Siebert, K.G. and Veeser, A., Pointwise a posteriori error control for elliptic obstacle problems. Numer. Math. 95 (2003) 163–195. CrossRef
Nochetto, R.H., Siebert, K.G. and Veeser, A., Fully localized a posteriori error estimators and barrier sets for contact problems. SIAM J. Numer. Anal. 42 (2005) 2118–2135. CrossRef
Picasso, M., Adaptive finite elements for a linear parabolic problem. Comput. Methods Appl. Mech. Engrg. 167 (1998) 223–237. CrossRef
A. Schmidt and K.G. Siebert, Design of adaptive finite element software: the finite element toolbox ALBERTA. Lecture Notes in Computational Science and Engineering, Springer (2005).
Veeser, A., Efficient and reliable a posteriori error estimators for elliptic obstacle problems. SIAM J. Numer. Anal. 39 (2001) 146–167. CrossRef
R. Verfürth, A review of a posteriori error estimation and adaptive mesh-refinement techniques. Wiley Teubner (1996).
Verfürth, R., A posteriori error estimates for finite element discretizations of the heat equation. Calcolo 40 (2003) 195–212. CrossRef
von Petersdorff, T. and Schwab, C., Numerical solution of parabolic equations in high dimensions. ESAIM: M2AN 38 (2004) 93–127. CrossRef
Vuik, C., An L 2-error estimate for an approximation of the solution of a parabolic variational inequality. Numer. Math. 57 (1990) 453–471. CrossRef
P. Wilmott, J. Dewynne, and S. Howison, Option Pricing: Mathematical Models and Computation. Oxford Financial Press, Oxford, UK (1993).