One may produce the qth harmonic of a string of length π by applying the 'correct touch' at the node $\pi/q$ during a simultaneous pluck or bow. This notion wasmade precise by a model of Bamberger, Rauch and Taylor. Their 'touch' isa damper of magnitude b concentrated at $\pi/q$ . The 'correct touch' is that b for which the modes, that do not vanishat $\pi/q$ , are maximally damped. We here examine the associated spectralproblem. We find the spectrum to be periodic and determined by a polynomialof degree $q-1$ . We establish lower and upper bounds on the spectral abscissaand show that the set of associated root vectors constitutes a Riesz basisand so identify 'correct touch' with the b that minimizes the spectral abscissa.

Among ${\mathbb R}^3$ -valued triples of random vectors (X,Y,Z) having fixed marginal probability laws, what is the best way to jointly draw (X,Y,Z) in such a way that the simplex generated by (X,Y,Z) has maximal average volume? Motivated by this simple question, we study optimal transportation problems with several marginals when the objective function is the determinant or its absolute value.

Several recent results in the area of robust asymptotic stability of hybrid systems show that the concept of a generalized solution to a hybrid system is suitable for the analysis and design of hybrid control systems. In this paper, we show that such generalized solutions are exactly the solutions that arise when measurement noise in the system is taken into account.

The aim of this paper is to study problems of the form: $inf_{(u\in V)}J(u)$ 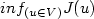with $J(u):=\int_0^1 L(s,y_u(s),u(s)){\rm d}s+g(y_u(1))$ 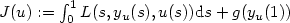where V is a set of admissible controls and y u is the solution of the Cauchy problem: $\dot{x}(t) =\langle f(.,x(.)), \nu_t \rangle + u(t), t \in (0,1)$ 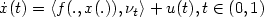, $x(0) = x_{\rm 0}$ 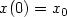and each $\nu_t$ 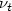is a nonnegative measure with support in [0,t]. After studying the Cauchy problem, we establish existence of minimizers, optimality conditions (in particular in the form of a nonlocal version of the Pontryagin principle) and prove some regularity results. We also consider the more general case where the control also enters the dynamics in a nonlocal way.

In this work we study the nonlinear complementarity problem on thenonnegative orthant. This is done by approximating its equivalentvariational-inequality-formulation by a sequence of variationalinequalities with nested compact domains. This approach yieldssimultaneously existence, sensitivity, and stability results. Byintroducing new classes of functions and a suitable metric forperforming the approximation, we provide bounds for the asymptoticset of the solution set and coercive existence results, which extendand generalize most of the existing ones from the literature. Suchresults are given in terms of some sets called coercive existencesets, which we also employ for obtaining new sensitivity andstability results. Topological properties of thesolution-set-mapping and bounds for it are also established.Finally, we deal with the piecewise affine case.

By means of a direct and constructive method based on the theory of semi-global C 1 solution, the local exact boundary observability is established for one-dimensional first order quasilinear hyperbolic systems with general nonlinear boundary conditions. An implicit duality between the exact boundary controllability and the exact boundary observability is then shown in the quasilinear case.

In this paper, we solve an optimal control problem using thecalculus of variation. The system under consideration is aswitched autonomous delay system that undergoes jumps at theswitching times. The control variables are the instants when theswitches occur, and a set of scalars which determine the jumpamplitudes. Optimality conditions involving analytic expressionsfor the partial derivatives of a given cost function with respectto the control variables are derived using the calculus ofvariation. A locally optimal impulsive control strategy can thenbe found using a numerical gradient descent algorithm.

We study variational problems with volume constraints, i.e., with level sets of prescribed measure. We introduce a numerical method to approximate local minimizers and illustrate it with some two-dimensional examples. We demonstrate numerically nonexistence results which had been obtained analytically in previous work. Moreover, we show the existence of discontinuous dependence of global minimizers from the data by using a Γ-limit argument and illustrate this with numerical computations. Finally we construct explicitly local and global minimizers for problems with two volume constraints.

Let W be a function from the real m×n-matrices to the real numbers. If W is quasiconvex in the sense of the calculus of variations, then we show that W can be approximated locally uniformly by quasiconvex polynomials.

Here we present an approximation method for a rather broad class of first ordervariational problems in spaces of piece-wise constant functions overtriangulations of the base domain. The convergence of the method is based on aninequality involving $W^{-1, p}$ norms obtained by Nečas and on the generalframework of Γ-convergence theory.

The paper deals with an optimal control problem with a scalar first-order state constraint and a scalar control.In presence of (nonessential) touch points,the arc structure of the trajectory is not stable.Under some reasonable assumptions,we show that boundary arcs are structurally stable, and that touch point can either remain so, vanish or be transformed into a single boundary arc. Assuming a weak second-order optimality condition (equivalent to uniform quadratic growth), stability and sensitivity results are given. The main tools are the study of a quadratic tangent problem and the notion of strong regularity.Those results enable us to design a new continuation algorithm,presented at the end of the paper, that handles automatically changes in the structure of the trajectory.

The irrigation problem is the problem of finding an efficient way to transport a measure μ+onto a measure μ-. By efficient, we mean that a structure that achieves the transport (which, following [Bernot, Caselles and Morel, Publ. Mat.49 (2005) 417–451], we call traffic plan)is better if it carries the mass in a grouped way rather than in a separate way.This is formalized by considering costs functionals that favorize this property.The aim of this paper is to introduce a dynamical cost functional on traffic plans that we argue to be more realistic.The existence of minimizers is proved in two ways: in some cases, we can deduce it from a classical semicontinuity argument; the other cases are treated by studying the link between our cost and the one introduced in [Bernot, Caselles and Morel, Publ. Mat.49 (2005) 417–451].Finally, we discuss the stability of minimizers with respect to specific variations of the cost functional.

Given a Borel function ψ defined on a bounded open set Ω with Lipschitz boundary and $\varphi\in L^1(\partial\Omega,{\mathcal H}^{n-1})$ , we prove an explicit representation formula for the L 1 lower semicontinuous envelope of Mumford-Shah type functionals with the obstacle constraint $u^+\ge\psi$ ${\mathcal H}^{n-1}$ a.e. on Ω and the Dirichlet boundary condition $u=\varphi$ on $\partial\Omega$ .

The Linear-Quadratic (LQ) optimal control problem is studied for aclass of first-order hyperbolic partial differential equation modelsby using a nonlinear infinite-dimensional (distributed parameter) Hilbert state-spacedescription. First the dynamical properties of the linearized modelaround some equilibrium profile are studied. Next the LQ-feedbackoperator is computed by using the corresponding operator Riccatialgebraic equation whose solution is obtained via a relatedmatrix Riccati differential equation in the space variable. Then thelatter is applied to the nonlinear model, and the resultingclosed-loop system dynamical performances are analyzed.