Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-09T15:28:46.670Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal transportation for the determinant

Published online by Cambridge University Press:  18 January 2008

Guillaume Carlier  and
Bruno Nazaret
Guillaume Carlier
Affiliation:
CEREMADE, UMR CNRS 7534, Université Paris Dauphine, Pl. de Lattre de Tassigny, 75775 Paris Cedex 16, France; [email protected]; [email protected]
Bruno Nazaret
Affiliation:
CEREMADE, UMR CNRS 7534, Université Paris Dauphine, Pl. de Lattre de Tassigny, 75775 Paris Cedex 16, France; [email protected]; [email protected]
Get access

Abstract

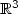Among ${\mathbb R}^3$ -valued triples of random vectors (X,Y,Z) having fixed marginal probability laws, what is the best way to jointly draw (X,Y,Z) in such a way that the simplex generated by (X,Y,Z) has maximal average volume? Motivated by this simple question, we study optimal transportation problems with several marginals when the objective function is the determinant or its absolute value.

Keywords

Optimal transportationmulti-marginals problemsdeterminantdisintegrations
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 14 , Issue 4 , October 2008 , pp. 678 - 698
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brenier, Y., Polar factorization and monotone rearrangements of vector valued functions. Comm. Pure Appl. Math. 44 (1991) 375–417. CrossRef
B. Dacorogna, Direct methods in the calculus of variations, Applied Mathematical Sciences 78. Springer-Verlag, Berlin (1989).
Ekeland, I., A duality theorem for some non-convex functions of matrices. Ric. Mat. 55 (2006) 1–12. CrossRef
I. Ekeland and R. Temam, Convex Analysis and Variational Problems, in Classics in Mathematics, Society for Industrial and Applied Mathematics, Philadelphia (1999).
Gangbo, W. and A. Święch, Optimal maps for the multidimensional Monge-Kantorovich problem. Comm. Pure Appl. Math. 51 (1998) 23–45. 3.0.CO;2-H>CrossRef
W. Gangbo and R.J. McCann, The geometry of optimal transportation. Acta Math. 177 (1996) 113–161.
S.T. Rachev and L. Rüschendorf, Mass Transportation Problems. Vol. I: Theory; Vol. II: Applications. Springer-Verlag (1998).
C. Villani, Topics in optimal transportation, Graduate Studies in Mathematics 58. American Mathematical Society, Providence, RI (2003).