Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T04:21:40.058Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on exact controllability for the Navier-Stokes equations

Published online by Cambridge University Press:  15 August 2002

Oleg Yu. Imanuvilov
Oleg Yu. Imanuvilov*
Affiliation:
Department of Mathematics, Iowa State University, 400 Carver Hall, Ames, IA 50011-2064, U.S.A.; [email protected].
Get access

Abstract

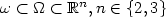We study the local exact controllability problem for the Navier-Stokes equations that describe an incompressible fluid flow in a bounded domain Ω with control distributed in a subdomain $\omega\subset\Omega\subset \mathbb{R}^n, n\in\{2,3\}$. The result that we obtained in this paper is as follows. Suppose that $\hat v(t,x)$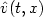 is a given solution of the Navier-Stokes equations. Let $ v_0(x)$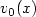 be a given initial condition and $\Vert \hat v(0,\cdot) - v_0 \Vert < \varepsilon$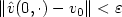 where ε is small enough. Then there exists a locally distributed control $u, \text{supp}\, u\subset (0,T)\times \omega $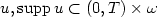 such that the solution v(t,x) of the Navier-Stokes equations: $$ \partial_tv-\Delta v+(v,\nabla)v=\nabla p+u+f, \,\, \text{\rm div}\, v=0,\,\, v\vert_{\partial\Omega}=0, \,\, v \vert_{t=0} = v_0 $$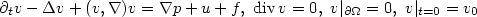 coincides with $\hat v(t,x)$ 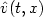at the instant T : $v(T,x) \equiv \hat v(T,x)$.

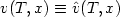Keywords

Locally distributed controlNavier-Stokes system.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 6 , 2001 , pp. 39 - 72
Copyright
© EDP Sciences, SMAI, 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

V.M. Alekseev, V.M. Tikhomirov and S.V. Fomin, Optimal control. Consultants Bureau, New York (1987).
Chae, D., Imanuvilov, O.Yu. and Kim, S.M., Exact controllability for semilinear parabolic equations with Neumann boundary conditions. J. Dynam. Control Systems 2 (1996) 449-483. CrossRef
Coron, J.-M., On the controllability of the 2-D incompressible Navier-Stokes equations with the Navier-Slip boundary conditions. ESAIM: COCV 1 (1996) 35-75. CrossRef
Coron, J.-M., On the controllability of 2-D incompressible perfect fluids. J. Math. Pures Appl. 75 (1996) 155-188.
Coron, J.-M., Contrôlabilité exacte frontière de l'équation d'Euler des fluides parfaits incompressibles bidimensionnels. C. R. Acad. Sci. Paris Sér. I Math. 317 (1993) 271-276.
Coron, J.-M. and Fursikov, A.V., Global exact controllability of the 2-D Navier-Stokes equations on manifold without boundary. Russian J. Math. Phys. 4 (1996) 1-20.
Fabre, C., Résultats d'unicité pour les équations de Stokes et applications au contrôle. C. R. Acad. Sci. Paris Sér. I Math. 322 (1996) 1191-1196.
Fabre, C. and Lebeau, G., Prolongement unique des solutions de l'équation de Stokes. Comm. Partial Differential Equations 21 (1996) 573-596. CrossRef
Fursikov, A.V. and Imanuvilov, O.Yu., Local exact controllability of two dimensional Navier-Stokes system with control on the part of the boundary. Sb. Math. 187 (1996) 1355-1390. CrossRef
Fursikov, A.V. and Imanuvilov, O.Yu., Local exact boundary controllability of the Boussinesq equation. SIAM J. Control Optim. 36 (1988) 391-421. CrossRef
Fursikov, A.V. and Imanuvilov, O.Yu., Local exact controllability of the Navier-Stokes Equations. C. R. Acad. Sci. Paris Sér. I Math. 323 (1996) 275-280.
A.V. Fursikov and O.Yu. Imanuvilov, Controllability of evolution equations, Lecture notes series (1996), no. 34 SNU, Seoul.
Fursikov, A.V. and Imanuvilov, O.Yu., On approximate controllability of the Stokes system. Ann. Fac. Sci. Toulouse 11 (1993) 205-232. CrossRef
Fursikov, A.V. and Imanuvilov, O.Yu., Exact controllability of the Navier-Stokes equations and the Boussinesq system. Russian Math. Surveys 54 (1999) 565-618. CrossRef
O. Glass, Contrôlabilité de l'équation d'Euler tridimensionnelle pour les fluides parfaits incompressibles, Séminaire sur les Équations aux Dérivées Partielles, 1997-1998, Exp No XV. École Polytechnique, Palaiseau (1998) 11.
O. Glass, Contrôlabilité exacte frontière de l'équation d'Euler des fluides parfaits incompressibles en dimension 3. C. R. Acad. Sci. Paris Sér. I Math. (1997) 987-992.
L. Hörmander, Linear partial differential operators. Springer-Verlag, Berlin (1963).
Horsin, T., On the controllability of the Burgers equations. ESAIM: COCV 3 (1998) 83-95. CrossRef
Imanuvilov, O.Yu., On exact controllability for the Navier-Stokes equations. ESAIM: COCV 3 (1998) 97-131. CrossRef
Imanuvilov, O.Yu., Boundary controllability of parabolic equations. Sb. Math. 186 (1995) 879-900.
Imanuvilov, O.Yu., Local exact controllability for the 2-D Navier-Stokes equations with the Navier slip boundary conditions. Lecture Notes in Phys. 491 (1977) 148-168. CrossRef
O.Yu. Imanuvilov and M. Yamamoto, On Carleman inequalities for parabolic equations in Sobolev spaces of negative order and exact controllability for semilinear parabolic equations, UTMS 98-46.
A.N. Kolmogorov and S.V. Fomin, Introductory real analysis. Dover Publications, INC, New York (1996).
O.A. Ladyzenskaja and N.N. Ural'ceva, Linear and quasilinear equations of elliptic type. Academic Press, New York (1968).
J.L. Lions, Contrôle des systèmes distribués singuliers. Gauthier-Villars, Paris (1983).
J.L. Lions, Optimal control of systems governed by partial differential equations. Springer-Verlag (1971).
J.-L. Lions, Are there connections between turbulence and controllability?, in 9 e Conférence internationale de l'INRIA. Antibes (1990).
J.-L. Lions and E. Magenes, Non-Homogeneous Boundary Value Problems. Springer-Verlag, Berlin (1971).
M. Taylor, Pseudodifferential operators. Princeton Univ. Press (1981).
M. Taylor, Pseudodifferential operators and Nonlinear PDE. Birkhäuser (1991).
R. Temam, Navier-Stokes equations. North-Holland Publishing Company, Amsterdam (1979).