Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T22:03:12.785Z Has data issue: false hasContentIssue false
  • English
  • Français

Homogenization of evolution problems for a composite medium with very small and heavy inclusions

Published online by Cambridge University Press:  15 March 2005

Michel Bellieud
Michel Bellieud*
Affiliation:
Département de Mathématiques, Université de Perpignan, 52 av. de Villeneuve, 66100 Perpignan, France; [email protected]
Get access

Abstract

We study the homogenization of parabolic or hyperbolic equations like \[\rho_\varepsilon{\partial^n u_\varepsilon\over \partial t^n}- {\rm div}(a_\varepsilon\nabla u_\varepsilon) =f \ \ \hbox{ in } \quad {\O\times(0,T)}+\ \ \hbox{\rm boundary conditions}, \quad n \in \{1,2\},\] 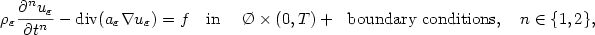when the coefficients $\rho_\varepsilon$ 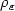, $a_\varepsilon$ 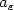(defined in Ω) take possibly high values on a ε-periodic set of grain-like inclusions of vanishing measure.Memory effects arise in the limit problem.

Keywords

Homogenizationmemory effectsgrain-like inclusions.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 11 , Issue 2 , April 2005 , pp. 266 - 284
Copyright
© EDP Sciences, SMAI, 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bellieud, M., Homogenization of evolution problems in a fiber reinforced structure. J. Convex Anal. 11 (2004) 363–385.
Bellieud, M. and Bouchitté, G., Homogenization of elliptic problems in a fiber reinforced structure. Non local effects. Ann. Scuola Norm. Sup. Cl. Sci. IV 26 (1998) 407–436.
M. Bellieud and I. Gruais, Homogénéisation d'une structure élastique renforcée de fibres très rigides. Effets non locaux. C. R. Math., Problèmes mathématiques de la mécanique 337 (2003) 493–498.
Bellieud, M. and Gruais, I., Homogenization of an elastic material reinforced by very stiff or heavy fibers. Non local effects. Memory effects. J. Math. Pures Appl. 84 (2005) 55–96. CrossRef
H. Brezis, Analyse fonctionnelle. Masson, Paris (1983).
G. Dal Maso, An introduction to $ \Gamma $ -Convergence. Progress Nonlinear Differential Equations Appl., Birkhäuser, Boston (1993).
E.Y. Khruslov, Homogenized models of composite media. Progress Nonlinear Differential Equations Appl., Birkhäuser (1991).
J.L. Lions and E. Magenes, Problèmes aux limites non homogènes et applications. Dunod, Paris 1 (1968).
Mosco, U., Composite media and asymptotic Dirichlet forms. J. Funct. Anal. 123 (1994) 368–421. CrossRef
Panasenko, G., Multicomponent homogenization of the vibration problem for incompressible media with heavy and rigid inclusions. C. R. Acad. Sci. Paris I 321 (1995) 1109–1114.