Article contents
A Two Well Liouville Theorem
Published online by Cambridge University Press: 15 July 2005
Abstract
In this paper we analyse the structure of approximate solutions to the compatible two well problem with the constraint that the surface energy of the solution is less than some fixed constant. We prove a quantitative estimate that can be seen as a two well analogue of the Liouville theorem of Friesecke James Müller.
Let $H=\bigl(\begin{smallmatrix} \sigma& 00 & \sigma^{-1} \end{smallmatrix}\bigr)$ 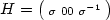 for $\sigma>0$
for $\sigma>0$ 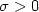 . Let $0<\zeta_1<1<\zeta_2<\infty$
. Let $0<\zeta_1<1<\zeta_2<\infty$ 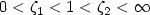 . Let $K:=SO\left(2\right)\cup SO\left(2\right)H$
. Let $K:=SO\left(2\right)\cup SO\left(2\right)H$ 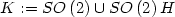 .Let $u\in W^{2,1}\left(Q_{1}\left(0\right)\right)$
.Let $u\in W^{2,1}\left(Q_{1}\left(0\right)\right)$ 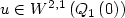 be a $\xCone$
be a $\xCone$ 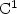 invertible bilipschitz function with $\mathrm{Lip}\left(u\right)<\zeta_2$
invertible bilipschitz function with $\mathrm{Lip}\left(u\right)<\zeta_2$ 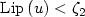 , $\mathrm{Lip}\left(u^{-1}\right)<\zeta_1^{-1}$
, $\mathrm{Lip}\left(u^{-1}\right)<\zeta_1^{-1}$ 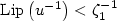 .
There exists positive constants $\mathfrak{c}_1<1$
.
There exists positive constants $\mathfrak{c}_1<1$  and $\mathfrak{c}_2>1$
and $\mathfrak{c}_2>1$ 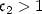 depending only on σ, $\zeta_1$
depending only on σ, $\zeta_1$ 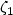 , $\zeta_2$
, $\zeta_2$ 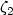 such that if $\epsilon\in\left(0,\mathfrak{c}_1\right)$
such that if $\epsilon\in\left(0,\mathfrak{c}_1\right)$ 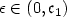 and u satisfies the following inequalities \[ \int_{Q_{1}\left(0\right)} {\rm d}\left(Du\left(z\right),K\right) {\rm d}L^2 z\leq \epsilon\]
and u satisfies the following inequalities \[ \int_{Q_{1}\left(0\right)} {\rm d}\left(Du\left(z\right),K\right) {\rm d}L^2 z\leq \epsilon\] 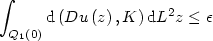 \[ \int_{Q_{1}\left(0\right)} \left|D^2 u\left(z\right)\right| {\rm d}L^2 z\leq \mathfrak{c}_1,\]
\[ \int_{Q_{1}\left(0\right)} \left|D^2 u\left(z\right)\right| {\rm d}L^2 z\leq \mathfrak{c}_1,\] 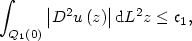 then there exists $J\in\left\{Id,H\right\}$
then there exists $J\in\left\{Id,H\right\}$ 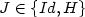 and $R\in SO\left(2\right)$
and $R\in SO\left(2\right)$ 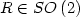 such that \[ \int_{Q_{\mathfrak{c}_1}\left(0\right)} \left|Du\left(z\right)-RJ\right| {\rm d}L^2 z\leq \mathfrak{c}_2\epsilon^{\frac{1}{800}}.\]
such that \[ \int_{Q_{\mathfrak{c}_1}\left(0\right)} \left|Du\left(z\right)-RJ\right| {\rm d}L^2 z\leq \mathfrak{c}_2\epsilon^{\frac{1}{800}}.\] 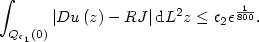
Keywords
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 11 , Issue 3 , July 2005 , pp. 310 - 356
- Copyright
- © EDP Sciences, SMAI, 2005
References
- 9
- Cited by


