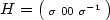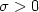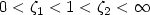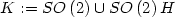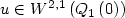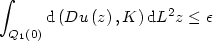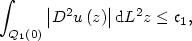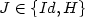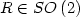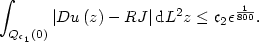Research Article
A Two Well Liouville Theorem
-
- Published online by Cambridge University Press:
- 15 July 2005, pp. 310-356
-
- Article
- Export citation
Vector variational problems and applications to optimal design
-
- Published online by Cambridge University Press:
- 15 July 2005, pp. 357-381
-
- Article
- Export citation
Conical differentiability for bone remodelingcontact rod models
-
- Published online by Cambridge University Press:
- 15 July 2005, pp. 382-400
-
- Article
- Export citation
The topological asymptotic for the Navier-Stokes equations
-
- Published online by Cambridge University Press:
- 15 July 2005, pp. 401-425
-
- Article
- Export citation
Null-controllability of some systems of parabolic typeby one control force
-
- Published online by Cambridge University Press:
- 15 July 2005, pp. 426-448
-
- Article
- Export citation
The nonlinear membrane model: a Young measureand varifold formulation
-
- Published online by Cambridge University Press:
- 15 July 2005, pp. 449-472
-
- Article
- Export citation
Unique continuation and decay for the Korteweg-de Vries equation withlocalized damping
-
- Published online by Cambridge University Press:
- 15 July 2005, pp. 473-486
-
- Article
- Export citation
Asymptotic stability of linear conservative systemswhen coupledwith diffusive systems
-
- Published online by Cambridge University Press:
- 15 July 2005, pp. 487-507
-
- Article
- Export citation