Article contents
The Lazy Travelling Salesman Problem in $\mathbb{R}^2$ 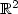
Published online by Cambridge University Press: 20 June 2007
Abstract
We study a parameter (σ)dependent relaxation of the Travelling Salesman Problem on $\mathbb{R}^2$ 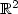 .The relaxed problem is reduced to the Travelling Salesman Problemas $\sigma\rightarrow$
.The relaxed problem is reduced to the Travelling Salesman Problemas $\sigma\rightarrow$ 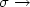 0. For increasing σ it is also anordered clustering algorithm for a set of points in $\mathbb{R}^2$
0. For increasing σ it is also anordered clustering algorithm for a set of points in $\mathbb{R}^2$ 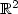 .A dual formulation is introduced, which reduces the problem to aconvex optimization, provided the minimizer is in the domain ofconvexity of the relaxed functional. It is shown that this lastcondition is generically satisfied, provided σ is largeenough.
.A dual formulation is introduced, which reduces the problem to aconvex optimization, provided the minimizer is in the domain ofconvexity of the relaxed functional. It is shown that this lastcondition is generically satisfied, provided σ is largeenough.
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 3 , July 2007 , pp. 538 - 552
- Copyright
- © EDP Sciences, SMAI, 2007
References
- 3
- Cited by


