Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T18:40:50.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact null internal controllability for the heat equation on unbounded convex domains∗

Published online by Cambridge University Press:  27 January 2014

Viorel Barbu
Viorel Barbu*
Affiliation:
Al.I. Cuza University and Octav Mayer Institute of Mathematics (Romanian Academy), Iaşi, Romania. [email protected]
Get access

Abstract

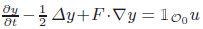The liner parabolic equation \hbox{$\frac{\pp y}{\pp t}-\frac12\,\D y+F\cdot\na y={\vec{1}}_{\calo_0}u$}∂y∂t−12 Δy+F·∇y=1𝒪0u with Neumann boundary condition on a convex open domain 𝒪 ⊂ ℝdwith smooth boundary is exactly null controllable on each finite interval if 𝒪0is an open subset of 𝒪which contains a suitable neighbourhood of the recession cone of \hbox{$\ov\calo$}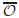𝒪. Here, F : ℝd → ℝd is a bounded, C1-continuous function, and F = ∇g, where g is convex and coercive.

Keywords

Parabolic equationnull controllabilityconvex setCarleman inequality
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 20 , Issue 1 , January 2014 , pp. 222 - 235
Copyright
© EDP Sciences, SMAI, 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aniţa, S. and Barbu, V., Null controllability of nonlinear convective heat equation. ESAIM: COCV 5 (2000) 157–173. Google Scholar
Barbu, V., Exact controllability of the superlinear heat equations. Appl. Math. Optim. 42 (2000) 73–89. Google Scholar
Barbu, V., Controllability of parabolic and Navier-Stokes equations. Scientiae Mathematicae Japonicae 56 (2002) 143–211. Google Scholar
Barbu, V. and Da Prato, G., The Neumann problem on unbounded domains of Rd and stochastic variational inequalities. Commun. Partial Differ. Eq. 11 (2005) 1217–1248. Google Scholar
Barbu, V. and Da Prato, G., The generator of the transition semigroup corresponding to a stochastic variational inequality. Commun. Partial Differ. Eq. 33 (2008) 1318–1338. Google Scholar
Bogachev, V.I., Krylov, N.V. and Röckner, M., On regularity of transition probabilities and invariant measures of singular diffusions under minimal conditions. Commun. Partial Differ. Eq. 26 (2001) 11–12. Google Scholar
Cepá, E., Multivalued stochastic differential equations. C.R. Acad. Sci. Paris, Ser. 1, Math. 319 (1994) 1075–1078. Google Scholar
Dubova, A., Fernandez Cara, E. and Burges, M., On the controllability of parabolic systems with a nonlinear term involving state and gradient. SIAM J. Control Optim. 41 (2002) 718–819. Google Scholar
Dubova, A., Osses, A. and Puel, J.P., Exact controllability to trajectories for semilinear heat equations with discontinuous coefficients. ESAIM: COCV 8 (2002) 621–667. Google Scholar
Fernandez Cara, E. and Guerrero, S., Global Carleman inequalities for parabolic systems and applications to controllability. SIAM J. Control Optim. 45 (2006) 1395–1446. Google Scholar
E. Fernandez Cara and E. Zuazua, Null and approximate controllability for weakly blowing up semilinear heat equations, vol. 17 of Annales de l’Institut Henri Poincaré (C) Nonlinear Analysis (2000) 583–616.
A. Fursikov, Imanuvilov and O. Yu, Controllability of Evolution Equations, Lecture Notes #34. Seoul National University Korea (1996).
Lebeau, G. and Robbiano, L., Contrôle exact de l’équation de la chaleur. Commun. Partial Differ. Eq. 30 (1995) 335–357. Google Scholar
Le Rousseau, J. and Lebeau, G., On Carleman estimates for elliptic and parabolic operators. Applicatiosn to unique continuation and control of parabolic equations. ESAIM: COCV 18 (2012) 712–747. Google Scholar
Le Rousseau, J. and Robbiano, L., Local and global Carleman estimates for parabolic operators with coefficients with jumps at interfaqces. Inventiones Mathematicae 183 (2011) 245–336. Google Scholar
Micu, S. and Zuazua, E., On the lack of null controllability of the heat equation on the half-line. Trans. AMS 353 (2000) 1635–1659. Google Scholar
Micu, S. and Zuazua, E., On the lack of null controllability of the heat equation on the half-space. Part. Math. 58 (2001) 1–24. Google Scholar
Miller, L., Unique continuation estimates for the Laplacian and the heat equation on non-compact manifolds, Math. Res. Lett. 12 (2005) 37–47. Google Scholar
R.T. Rockafellar, Convex Analysis. Princeton University Press, Princeton, N.Y. (1970).
C. Zalinescu, Convex Analysis in General Vector Spaces. World Scientific Publishing, River Edge, N.Y. (2002).
Zhang, Xu, A unified controllability/observability theory for some stochastic and deterministic partial differential equations, Proc. of the International Congress of Mathematicians, vol. IV, 3008-3034. Hindustan Book Agency, New Delhi (2010).
X. Zhang and E. Zuazua, On the optimality of the observability inequalities for Kirchoff plate systems with potentials in unbounded domains, in Hyperbolic Prloblems: Theory, Numerics and Applications, edited by S. Benzoni-Gavage and D. Serre. Springer (2008) 233–243.