Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T09:29:51.949Z Has data issue: false hasContentIssue false
  • English
  • Français

Computation of the distance to semi-algebraic sets

Published online by Cambridge University Press:  15 August 2002

Christophe Ferrier
Christophe Ferrier*
Affiliation:
Département Mathématiques Appliquées et Analyse Numérique, Centre National d'Études Spatiales, 18 avenue E. Belin, 31401 Toulouse Cedex 4, France; [email protected].
Get access

Abstract

This paper is devoted to the computation of distance to set, called S, defined by polynomial equations. First we consider the case of quadratic systems. Then, application of results stated for quadratic systems to the quadratic equivalent of polynomial systems (see [5]), allows us to compute distance to semi-algebraic sets. Problem of computing distance can be viewed as non convex minimization problem: $ d(u,S) = \inf_{x \in S} \| x-u\|^2$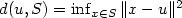, where u is in $\mathcal{R}^{n}$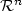. To have, at least, lower approximation of distance, we consider the dual bound m(u) associated with the dual problem and give sufficient conditions to guarantee m(u) = d(u,S). The second part deal with numerical computation of m(u) using an interior point method in semidefinite programming. Last, various examples, namely from chemistry and robotic, are given.

Keywords

Distancedual bondoptimality conditionspolynomial systemsinterior point methodssemidefinite programminglocation of zeros.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 5 , 2000 , pp. 139 - 156
Copyright
© EDP Sciences, SMAI, 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alizadeth, F., Interior point methods in semidefinite programming with application to combinatorial optimisation. SIAM J. Optim. 5 (1995) 13-51. CrossRef
A. Bellido, Construction de fonctions d'itération pour le calcul simultané des solutions d'équations et de systèmes d'équations algébriques. Thèse de doctorat de l'Universté Paul Sabatier, Toulouse (1992).
S. Boyd et al., Linear Matrix Inequalities Problem in Control Theory. SIAM, Philadelphia, Stud. Appl. Math. 15 (1995).
Dedieu, J.-P. and Yakoubsohn, J.-C., Localization of an algebraic hypersurface by the exclusion algorithm. Appl. Algebra Engrg. Comm. Comput. 2 (1992) 239-256. CrossRef
Ch. Ferrier, Hilbert's 17th problem and best dual bounds in quadratic minimization. Cybernetics and System Analysis 5 (1998) 76-91.
A.V. Fiacco and G.P. McCormick, Nonlinear Programming: Sequential Unconstrained Minimization Techniques. John Wiley (1968). Reprinted SIAM, 1990.
Fletcher, R., Semi-definite matrix constraints in optimization. SIAM J. Control Optim. 23 (1985) 493-513. CrossRef
C. Lemarechal and J.-B. Hiriart-Urruty, Convex Analysis and Minimization Algorithms II. Springer Verlag, Comprehensive Studies in Mathematics 306 (1991).
Jarre, F., Interior-point methods for convex programming. Appl. Math. Optim. 26 (1992) 287-391. CrossRef
Jarre, F., An interior-point method for minimizing the maximum eigenvalue of a linear combination of matrices. SIAM J. Control Optim. 31 (1993) 1360-1377. CrossRef
Karmarkar, N., A new polynomial-time algorithm for linear programming. Combinatorica 4 (1984) 373-395. CrossRef
Kearfott, R.B., Some tests of generalized bisection. ACM Trans. Math. Software 13 (1987) 197-200. CrossRef
Yu. Nesterov and A. Nemirovsky, Interior-point polynomial methods in convex programming. SIAM, Philadelphia, Stud. Appl. Math. 13 (1994).
Shor, N.Z., Dual estimate in multi-extremal problems. J. Global Optim. 2 (1992) 411-418. CrossRef
G. Sonnevend, An ``analytical centre'' for polyhedrons and a new classe of global algorithms for linear (smooth, convex) programming. Springer Verlag, Lecture Notes in Control and Inform. Sci. 84, System Modeling and Optimisation. 12th IFIP Conference on system optimisation 1984 (1986) 866-878.
Sonnevend, G. and Stoer, J., Global ellipsoidal approximation and homotopy methods for solving convex analitic programs. Appl. Math. Optim. 21 (1990) 139-165. CrossRef
D.E. Stewart, Matrix Computation in C. University of Queensland, Australia (1992). ftp site: [email protected]. directory: pub/meschach
Vandenberghe, L. and Boyd, S., Semidefinite programming. SIAM Rev. 1 (1996) 49-95. CrossRef
Verschelde, J., Verlinden, P. and Cools, R., Homotopy exploiting newton polytopes for solving sparse polynomials systems. SIAM J. Numer. Anal. 31 (1994) 915-930. CrossRef
Wright, A., Finding solutions to a system of polynomial equations. Math. Comp. 44 (1985) 125-133. CrossRef