Research Article
Mappings and homological properties in the Conley index theory
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 175-198
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 8 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
ETS volume 8 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 8 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b5
-
- Article
-
- You have access
- Export citation
Research Article
Destruction of invariant circles
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 199-214
-
- Article
-
- You have access
- Export citation
Bifurcations of relative equilibria in the 4- and 5-body problem
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 215-225
-
- Article
-
- You have access
- Export citation
Morse decompositions and connection matrices
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 227-249
-
- Article
-
- You have access
- Export citation
A stability theorem for minimal foliations on a torus
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 251-281
-
- Article
-
- You have access
- Export citation
Entropy and volume
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 283-299
-
- Article
-
- You have access
- Export citation
Isospectral sets for boundary value problems on the unit interval
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 301-358
-
- Article
-
- You have access
- Export citation
Connecting orbits in one-parameter families of flows
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 359-374
-
- Article
-
- You have access
- Export citation
Dynamical systems, shape theory and the Conley index
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 375-393
-
- Article
-
- You have access
- Export citation
Horseshoes for autonomous Hamiltonian systems using the Melnikov integral
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 395-409
-
- Article
-
- You have access
- Export citation
Front matter
ETS volume 8 special issue Cover and Front matter
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 8 special issue Cover and Back matter
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation

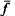 in be an exact, area-preserving, monotone twist diffeomorphism of the cylinder and let 10 be a Liouville number. We will show that arbitrarily close to
in be an exact, area-preserving, monotone twist diffeomorphism of the cylinder and let 10 be a Liouville number. We will show that arbitrarily close to 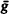 with no homotopically non-trivial invariant circle of rotation number ω.
with no homotopically non-trivial invariant circle of rotation number ω.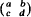 in SL(2,
in SL(2,