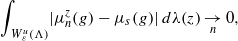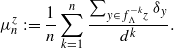Research Article
On a class of stable conditional measures
-
- Published online by Cambridge University Press:
- 01 November 2010, pp. 1499-1515
-
- Article
- Export citation
A variation formula for the topological entropy of convex-cocompact manifolds
-
- Published online by Cambridge University Press:
- 25 November 2010, pp. 1849-1864
-
- Article
- Export citation
The zeta functions of renewal systems
-
- Published online by Cambridge University Press:
- 26 March 2010, pp. 875-890
-
- Article
- Export citation
Invariant colorings of random planar maps
-
- Published online by Cambridge University Press:
- 22 April 2010, pp. 549-562
-
- Article
- Export citation
Equilibrium states for partially hyperbolic horseshoes
-
- Published online by Cambridge University Press:
- 18 January 2010, pp. 179-195
-
- Article
- Export citation
Vanishing transverse entropy in smooth ergodic theory
-
- Published online by Cambridge University Press:
- 27 September 2010, pp. 1229-1235
-
- Article
- Export citation
Diffeomorphisms which cannot be topologically conjugate to diffeomorphisms of a higher smoothness
-
- Published online by Cambridge University Press:
- 11 February 2010, pp. 563-569
-
- Article
- Export citation
Parallel chip-firing on the complete graph: Devil’s staircase and Poincaré rotation number
-
- Published online by Cambridge University Press:
- 06 May 2010, pp. 891-910
-
- Article
- Export citation
An example of a pathological random perturbation of the Cat Map
-
- Published online by Cambridge University Press:
- 25 May 2011, pp. 1865-1887
-
- Article
- Export citation
Diffeomorphisms with infinitely many irrational invariant curves
-
- Published online by Cambridge University Press:
- 23 November 2010, pp. 1517-1535
-
- Article
- Export citation
Fixed points of symplectic periodic flows
-
- Published online by Cambridge University Press:
- 16 June 2010, pp. 1237-1247
-
- Article
- Export citation
Multipliers of periodic orbits in spaces of rational maps
-
- Published online by Cambridge University Press:
- 11 March 2010, pp. 197-243
-
- Article
- Export citation
Ergodic decompositions associated with regular Markov operators on Polish spaces
-
- Published online by Cambridge University Press:
- 26 March 2010, pp. 571-597
-
- Article
- Export citation
Period-doubling cascades galore
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 1249-1267
-
- Article
- Export citation
Analytic integrability of quadratic–linear polynomial differential systems
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 245-258
-
- Article
- Export citation
Newhouse phenomenon and homoclinic classes
-
- Published online by Cambridge University Press:
- 17 November 2010, pp. 1537-1562
-
- Article
- Export citation
Asymptotic distributions of preimages for endomorphisms
-
- Published online by Cambridge University Press:
- 04 June 2010, pp. 911-934
-
- Article
- Export citation
Measures of maximal relative entropy with full support
-
- Published online by Cambridge University Press:
- 17 November 2010, pp. 1889-1899
-
- Article
- Export citation
Reducibility for a class of nonlinear quasi-periodic differential equations with degenerate equilibrium point under small perturbation
-
- Published online by Cambridge University Press:
- 10 March 2010, pp. 599-611
-
- Article
- Export citation
Existence of a measurable saturated compensation function between subshifts and its applications
-
- Published online by Cambridge University Press:
- 13 September 2010, pp. 1563-1589
-
- Article
- Export citation

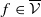 and there exists a dense set 𝒟⊂𝒱 such that for all
and there exists a dense set 𝒟⊂𝒱 such that for all 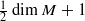 fixed points; this follows from Morse theory for the momentum map of the action. In this paper we use Atiyah–Bott–Berline–Vergne (ABBV) localization in equivariant cohomology to prove that this conclusion also holds for symplectic circle actions with non-empty fixed sets, as long as the Chern class map is somewhere injective—the Chern class map assigns to a fixed point the sum of the action weights at the point. We complement this result with less sharp lower bounds on the number of fixed points, under no assumptions; from a dynamical systems viewpoint, our results imply that there is no symplectic periodic flow with exactly one or two equilibrium points on a compact manifold of dimension at least eight.
fixed points; this follows from Morse theory for the momentum map of the action. In this paper we use Atiyah–Bott–Berline–Vergne (ABBV) localization in equivariant cohomology to prove that this conclusion also holds for symplectic circle actions with non-empty fixed sets, as long as the Chern class map is somewhere injective—the Chern class map assigns to a fixed point the sum of the action weights at the point. We complement this result with less sharp lower bounds on the number of fixed points, under no assumptions; from a dynamical systems viewpoint, our results imply that there is no symplectic periodic flow with exactly one or two equilibrium points on a compact manifold of dimension at least eight.