Research Article
Rigidity properties of Anosov optical hypersurfaces
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 707-737
-
- Article
- Export citation
Finite-rank Bratteli–Vershik diagrams are expansive
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 739-747
-
- Article
- Export citation
A new look at the crossed product of aC*-algebra by a semigroup of endomorphisms
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 749-789
-
- Article
- Export citation
On the Aubry–Mather theory for symbolic dynamics
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 791-815
-
- Article
- Export citation
Construction of foliations with prescribed separatrix
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 817-842
-
- Article
- Export citation
Topological entropy and partially hyperbolic diffeomorphisms
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 843-862
-
- Article
- Export citation
Proper minimal sets on compact connected 2-manifolds are nowhere dense
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 863-876
-
- Article
- Export citation
Denjoy systems and dimension groups
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 877-913
-
- Article
- Export citation
Geometric thermodynamic formalism and real analyticity for meromorphic functions of finite order
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 915-946
-
- Article
- Export citation
Basic dynamical stability results for
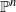
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 947-977
-
- Article
- Export citation
Linearization of holomorphic germs with quasi-parabolic fixed points
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 979-986
-
- Article
- Export citation
C1-stably shadowable chain components
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 987-1029
-
- Article
- Export citation
A non-constant invariant function for certain ergodic flows
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 1031-1035
-
- Article
- Export citation
Smoothness is not an obstruction to realizability
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 1037-1041
-
- Article
- Export citation
Erratum to ‘Semi-hyperbolic fibered rational maps and rational semigroups’ (Ergodic Theory and Dynamical Systems 26 (2006), 893–922)
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 1043-1045
-
- Article
- Export citation


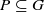 be a subsemigroup. In order to describe the crossed product of a
be a subsemigroup. In order to describe the crossed product of a 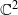 is built, with its analytical class of separatrix and holonomy representations prescribed. Thanks to this construction, we study the link between the moduli space of a foliation and the moduli space of its separatrix.
is built, with its analytical class of separatrix and holonomy representations prescribed. Thanks to this construction, we study the link between the moduli space of a foliation and the moduli space of its separatrix.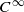 diffeomorphisms. The proof uses a topological invariant we introduced, Yomdin’s theorem on upper semi-continuity, Katok’s theorem on lower semi-continuity for two-dimensional systems, and a refined Pesin–Ruelle inequality we proved for partially hyperbolic diffeomorphisms.
diffeomorphisms. The proof uses a topological invariant we introduced, Yomdin’s theorem on upper semi-continuity, Katok’s theorem on lower semi-continuity for two-dimensional systems, and a refined Pesin–Ruelle inequality we proved for partially hyperbolic diffeomorphisms.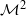 be a compact connected two-dimensional manifold, with or without boundary, and let
be a compact connected two-dimensional manifold, with or without boundary, and let 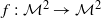 be a continuous map. We prove that if
be a continuous map. We prove that if 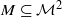 is a minimal set of the dynamical system
is a minimal set of the dynamical system 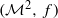 then either
then either 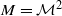 or
or 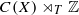 associated with (
associated with (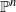
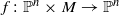 , we define the notion of a ‘Fatou section’, which is intuitively a choice of one point in
, we define the notion of a ‘Fatou section’, which is intuitively a choice of one point in 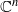 with the origin
with the origin 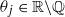 . We show that
. We show that 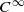 manifold
manifold 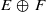 (where the dimension of
(where the dimension of 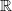 and let
and let 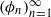 is said to be
is said to be 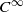 diffeomorphism of
diffeomorphism of 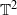 .
.