Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T04:00:52.929Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological entropy and partially hyperbolic diffeomorphisms

Published online by Cambridge University Press:  01 June 2008

YONGXIA HUA ,
RADU SAGHIN  and
ZHIHONG XIA
YONGXIA HUA
Affiliation:
Department of Mathematics, Northwestern University, Evanston, Illinois 60208, USA (email: [email protected], [email protected])
RADU SAGHIN
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, Canada M5S 2E4 (email: [email protected])
ZHIHONG XIA
Affiliation:
Department of Mathematics, Northwestern University, Evanston, Illinois 60208, USA (email: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider partially hyperbolic diffeomorphisms on compact manifolds. We define the notion of the unstable and stable foliations stably carrying some unique non-trivial homologies. 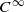Under this topological assumption, we prove the following two results: if the center foliation is one-dimensional, then the topological entropy is locally a constant; and if the center foliation is two-dimensional, then the topological entropy is continuous on the set of all diffeomorphisms. The proof uses a topological invariant we introduced, Yomdin’s theorem on upper semi-continuity, Katok’s theorem on lower semi-continuity for two-dimensional systems, and a refined Pesin–Ruelle inequality we proved for partially hyperbolic diffeomorphisms.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 3 , June 2008 , pp. 843 - 862
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Barreria, L. and Pesin, Y.. Smooth Ergodic Theory and Non-Uniformly Hyperbolic Dynamics (Handbook of Dynamical Systems, 1B). Elsevier, Amsterdam, 2005.Google Scholar
[2]Katok, A. and Mendoza, L.. Dynamical systems with non-uniformly hyperbolic behaviour. Introduction to the Modern Theory Dynamical Systems. Eds. A. Katok and B. Hasselblatt. Cambridge University Press, Cambridge, 1955.Google Scholar
[3]Pollicott, M.. Lectures on Ergodic Theory and Pesin Theory on Compact Manifolds (London Mathematical Society Lecture Note Series, 180). Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
[4]Robinson, C.. Dynamical Systems: Stability, Symbolic Dynamics, and Chaos, 2nd edn. CRC Press, Boca Raton, FL, 1999.Google Scholar
[5]Saghin, R. and Xia, Z.. Geometric expansion, Lyapunov exponents and foliations. Preprint, 2006.Google Scholar
[6]Walters, P.. Ergodic Theory (Lecture Notes in Mathematics, 458). Springer, Berlin, 1975.Google Scholar
[7]Walters, P.. An Introduction to Ergodic theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.CrossRefGoogle Scholar
[8]Yomdin, Y.. Volume growth and entropy. Israel J. Math. 57 (1987), 285–300.CrossRefGoogle Scholar