Research Article
Entropy pairs for a measure
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 621-632
-
- Article
- Export citation
Pseudogroups of isometries of ℝ: reconstruction of free actions on ℝ-trees
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 633-652
-
- Article
- Export citation
Ergodic properties of a dynamical system arising from percolation theory
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 653-661
-
- Article
- Export citation
On the sofic limit sets of cellular automata
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 663-684
-
- Article
- Export citation
Instances of cohomological triviality and rigidity
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 685-696
-
- Article
- Export citation
Classifying C1+ structures on dynamical fractals: 1. The moduli space of solenoid functions for Markov maps on train tracks
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 697-734
-
- Article
- Export citation
Persistence of homoclinic tangencies in higher dimensions
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 735-757
-
- Article
- Export citation
Cohomological rigidity of algebraic ℤd-actions
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 759-805
-
- Article
- Export citation
Conditional measure and flip invariance of Bowen-Margulis and harmonic measures on manifolds of negative curvature
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 807-811
-
- Article
- Export citation
Front matter
ETS volume 15 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 15 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b3
-
- Article
-
- You have access
- Export citation

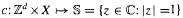 for an expansive and mixing ℤ
for an expansive and mixing ℤ