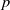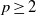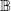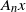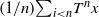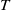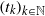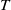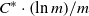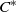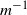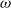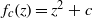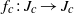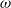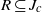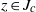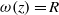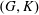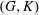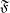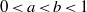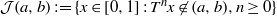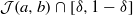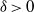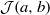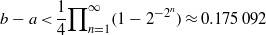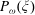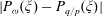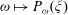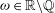Research Article
Oscillation and the mean ergodic theorem for uniformly convex Banach spaces
-
- Published online by Cambridge University Press:
- 10 January 2014, pp. 1009-1027
-
- Article
- Export citation
Rigorous pointwise approximations for invariant densities of non-uniformly expanding maps
-
- Published online by Cambridge University Press:
- 10 January 2014, pp. 1028-1044
-
- Article
-
- You have access
- Export citation
Shadowing and
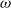 $\omega $-limit sets of circular Julia sets
$\omega $-limit sets of circular Julia sets
-
- Published online by Cambridge University Press:
- 14 November 2013, pp. 1045-1055
-
- Article
- Export citation
Gelfand pairs and strong transitivity for Euclidean buildings
-
- Published online by Cambridge University Press:
- 13 March 2014, pp. 1056-1078
-
- Article
- Export citation
Resonant motions in the presence of degeneracies for quasi-periodically perturbed systems
-
- Published online by Cambridge University Press:
- 26 February 2014, pp. 1079-1140
-
- Article
- Export citation
On rationally ergodic and rationally weakly mixing rank-one transformations
-
- Published online by Cambridge University Press:
- 26 February 2014, pp. 1141-1164
-
- Article
- Export citation
Modeling potential as fiber entropy and pressure as entropy
-
- Published online by Cambridge University Press:
- 26 February 2014, pp. 1165-1186
-
- Article
- Export citation
Aubry–Mather theory for homeomorphisms
-
- Published online by Cambridge University Press:
- 05 August 2014, pp. 1187-1207
-
- Article
- Export citation
The doubling map with asymmetrical holes
-
- Published online by Cambridge University Press:
- 14 November 2013, pp. 1208-1228
-
- Article
- Export citation
Foliations and conjugacy: Anosov structures in the plane
-
- Published online by Cambridge University Press:
- 14 March 2014, pp. 1229-1242
-
- Article
- Export citation
On the beta-expansions of 1 and algebraic numbers for a Salem number beta
-
- Published online by Cambridge University Press:
- 26 February 2014, pp. 1243-1262
-
- Article
- Export citation
Continuity of the Peierls barrier and robustness of laminations
-
- Published online by Cambridge University Press:
- 13 March 2014, pp. 1263-1288
-
- Article
- Export citation
Topological entropy of transitive dendrite maps
-
- Published online by Cambridge University Press:
- 14 November 2013, pp. 1289-1314
-
- Article
- Export citation
Topological enumeration of complex polynomial vector fields
-
- Published online by Cambridge University Press:
- 10 January 2014, pp. 1315-1344
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 35 Issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 May 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 35 Issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 May 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation