Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T04:52:39.499Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation and the mean ergodic theorem for uniformly convex Banach spaces

Published online by Cambridge University Press:  10 January 2014

JEREMY AVIGAD  and
JASON RUTE
JEREMY AVIGAD
Affiliation:
Philosophy and Mathematical Sciences, Carnegie Mellon University, Pittsburgh, USA email [email protected]
JASON RUTE
Affiliation:
Department of Mathematics, Pennsylvania State University, State College, PA 16802, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 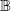$ \mathbb{B} $ be a 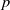$p$-uniformly convex Banach space, with 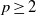$p\geq 2$. Let 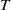$T$ be a linear operator on 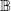$ \mathbb{B} $, and let 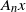${A}_{n} x$ denote the ergodic average 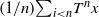$(1/ n){\mathop{\sum }\nolimits}_{i\lt n} {T}^{n} x$. We prove the following variational inequality in the case where 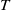$T$ is power bounded from above and below: for any increasing sequence 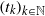$\mathop{({t}_{k} )}\nolimits_{k\in \mathbb{N} } $ of natural numbers we have 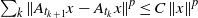${\mathop{\sum }\nolimits}_{k} \mathop{\Vert {A}_{{t}_{k+ 1} } x- {A}_{{t}_{k} } x\Vert }\nolimits ^{p} \leq C\mathop{\Vert x\Vert }\nolimits ^{p} $, where the constant 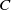$C$ depends only on 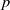$p$ and the modulus of uniform convexity. For 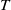$T$ a non-expansive operator, we obtain a weaker bound on the number of $\varepsilon $-fluctuations in the sequence. We clarify the relationship between bounds on the number of $\varepsilon $-fluctuations in a sequence and bounds on the rate of metastability, and provide lower bounds on the rate of metastability that show that our main result is sharp.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 4 , June 2015 , pp. 1009 - 1027
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, R. A. and Fournier, J. J. F.. Sobolev Spaces, 2nd edn. Elsevier/Academic Press, Amsterdam, 2003.Google Scholar
Avigad, J.. Uncomputably noisy ergodic limits. Notre Dame J. Form. Log. 53 (2012), 347–350.CrossRefGoogle Scholar
Avigad, J. and Iovino, J.. Ultraproducts and metastability. Preprint arXiv:1301.3063.Google Scholar
Avigad, J., Gerhardy, P. and Towsner, H.. Local stability of ergodic averages. Trans. Amer. Math. Soc. 362 (1) (2010), 261–288.CrossRefGoogle Scholar
Avigad, J. and Simic, K.. Fundamental notions of analysis in subsystems of second-order arithmetic. Ann. Pure Appl. Logic 139 (1–3) (2006), 138–184.CrossRefGoogle Scholar
Birkhoff, G.. The mean ergodic theorem. Duke Math. J. 5 (1) (1939), 19–20.CrossRefGoogle Scholar
Bishop, E.. An upcrossing inequality with applications. Michigan Math. J. 13 (1966), 1–13.CrossRefGoogle Scholar
Bishop, E.. Foundations of Constructive Analysis. McGraw-Hill, New York, 1967.Google Scholar
Bishop, E.. A constructive ergodic theorem. J. Math. Mech. 17 (1967/1968), 631–639.Google Scholar
Calderón, A. P.. Ergodic theory and translation-invariant operators. Proc. Natl. Acad. Sci. USA 59 (1968), 349–353.CrossRefGoogle ScholarPubMed
Carothers, N. L.. A Short Introduction to Banach Space Theory. Cambridge University Press, Cambridge, 2005.Google Scholar
Day, M. M.. Reflexive Banach spaces not isomorphic to uniformly convex spaces. Bull. Amer. Math. Soc. 47 (4) (1941), 313–317.CrossRefGoogle Scholar
Demeter, C.. Pointwise convergence of the ergodic bilinear Hilbert transform. Illinois J. Math. 51 (4) (2007), 1123–1158.CrossRefGoogle Scholar
Doob, J. L.. Stochastic Processes. John Wiley & Sons, New York, 1953.Google Scholar
Do, Y., Oberlin, R. and Palsson, E. A.. Variational bounds for a dyadic model of the bilinear Hilbert transform. Illinois J. Math. (to appear), arXiv:1203.5135.Google Scholar
Gerhardy, P. and Kohlenbach, U.. General logical metatheorems for functional analysis. Trans. Amer. Math. Soc. 360 (5) (2008), 2615–2660.CrossRefGoogle Scholar
Hochman, M.. Upcrossing inequalities for stationary sequences and applications. Ann. Probab. 37 (6) (2009), 2135–2149.CrossRefGoogle Scholar
Ivanov, V. V.. Oscillations of averages in the ergodic theorem. Dokl. Akad. Nauk 347 (6) (1996), 736–738.Google Scholar
Jones, R. L., Ostrovskii, I. V. and Rosenblatt, J. M.. Square functions in ergodic theory. Ergod. Th. & Dynam. Sys. 16 (2) (1996), 267–305.CrossRefGoogle Scholar
Jones, R. L., Kaufman, R., Rosenblatt, J. M. and Wierdl, M.. Oscillation in ergodic theory. Ergod. Th. & Dynam. Sys. 18 (4) (1998), 889–935.CrossRefGoogle Scholar
Jones, R. L., Rosenblatt, J. M. and Wierdl, M.. Oscillation in ergodic theory: higher dimensional results. Israel. J. Math. 135 (2003), 1–27.CrossRefGoogle Scholar
Kachurovskiĭ, A. G.. Rates of convergence in ergodic theorems. Uspekhi Mat. Nauk 51 (4(310)) (1996), 73–124; Translation in Russian Math. Surveys 51(4) (1996), 653–703.Google Scholar
Kalikow, S. and Weiss, B.. Fluctuations of ergodic averages. Illinois J. Math. 43 (3) (1999), 480–488.CrossRefGoogle Scholar
Kohlenbach, U.. Applied Proof Theory: Proof Interpretations and Their Use in Mathematics. Springer, Berlin, 2008.Google Scholar
Kohlenbach, U.. A uniform quantitative form of sequential weak compactness and Baillon’s nonlinear ergodic theorem. Commun. Contemp. Math. 14 (2012), 20 pages.CrossRefGoogle Scholar
Kohlenbach, U. and Leuştean, L.. Effective metastability of Halpern iterates in CAT(0) spaces. Adv. Math. 231 (2012), 2526–2556.CrossRefGoogle Scholar
Kohlenbach, U. and Leuştean, L.. A quantitative mean ergodic theorem for uniformly convex Banach spaces. Ergod. Th. & Dynam. Sys. 29 (6) (2009), 1907–1915; Erratum: Ergod. Th. & Dynam. Sys. 29(6) (2009) 1995.CrossRefGoogle Scholar
Kohlenbach, U. and Safarik, P.. Fluctuations, effective learnability and metastability in analysis. Ann. Pure Appl. Logic, to appear.Google Scholar
Krengel, U.. On the speed of convergence in the ergodic theorem. Monatsh. Math. 86 (1) (1978/79), 3–6.CrossRefGoogle Scholar
Krengel, U.. Ergodic Theorems. Walter de Gruyter & Co, Berlin, 1985.CrossRefGoogle Scholar
Lindenstrauss, J. and Tzafriri, L.. Classical Banach Spaces II: Function Spaces. Springer, Berlin, 1979.CrossRefGoogle Scholar
Maurey, B.. Type, cotype and $K$-convexity. Handbook of the Geometry of Banach Spaces, Vol. 2. North-Holland, Amsterdam, 2003, pp. 1299–1332.CrossRefGoogle Scholar
Oberlin, R., Seeger, A., Tao, T., Thiele, C. and Wright, J.. A variation norm Carleson theorem. J. Eur. Math. Soc. 14 (2012), 421–464.Google Scholar
Pisier, G.. Martingales with values in uniformly convex spaces. Israel. J. Math. 20 (3–4) (1975), 326–350.CrossRefGoogle Scholar
Pisier, G.. Probabilistic methods in the geometry of Banach spaces. Probability and Analysis (Varenna, 1985). Springer, Berlin, 1986, pp. 167–241.CrossRefGoogle Scholar
Pisier, G.. Martingales in Banach spaces (in connection with type and cotype). Course IHP, February 2–8, 2011. Manuscript, http://www.math.jussieu.fr/~pisier/ihp-pisier.pdf.Google Scholar
Pisier, G. and Xu, Q.. The strong $p$-variation of martingales and orthogonal series. Probab. Theory Related Fields 77 (1988), 497–514.CrossRefGoogle Scholar
Pour-El, M. B. and Ian Richards, J.. Computability in Analysis and Physics. Springer, Berlin, 1989.CrossRefGoogle Scholar
Sz.-Nagy, B., Bercovici, H., Foias, C. and Kérchy, L.. Harmonic Analysis of Operators on Hilbert Space. 2nd edn. Springer, New York, 2010.CrossRefGoogle Scholar
Schade, K. and Kohlenbach, U.. Effective metastability for modified Halpern iterations in CAT(0) spaces. Fixed Point Theory Appl. 2012:191 (2012), 19 pages.Google Scholar
Tao, T.. Norm convergence of multiple ergodic averages for commuting transformations. Ergod. Th. & Dynam. Sys. 28 (2) (2008), 657–688.CrossRefGoogle Scholar
V’yugin, V. V.. Ergodic convergence in probability, and an ergodic theorem for individual random sequences. Teor. Veroyatn. Primen. 42 (1) (1997), 35–50.Google Scholar
V’yugin, V. V.. Ergodic theorems for individual random sequences. Theoret. Comput. Sci. 207 (2) (1998), 343–361.CrossRefGoogle Scholar
Walsh, M.. Norm convergence of nilpotent ergodic averages. Ann. Math. 175 (3) (2012), 1667–1688.CrossRefGoogle Scholar