In this paper we consider ${C}^{1+ \epsilon } $ area-preserving diffeomorphisms of the torus $f$, either homotopic to the identity or to Dehn twists. We suppose that $f$ has a lift $\widetilde {f} $ to the plane such that its rotation set has interior and prove, among other things, that if zero is an interior point of the rotation set, then there exists a hyperbolic $\widetilde {f} $-periodic point $\widetilde {Q} \in { \mathbb{R} }^{2} $ such that ${W}^{u} (\widetilde {Q} )$ intersects ${W}^{s} (\widetilde {Q} + (a, b))$ for all integers $(a, b)$, which implies that $ \overline{{W}^{u} (\widetilde {Q} )} $ is invariant under integer translations. Moreover, $ \overline{{W}^{u} (\widetilde {Q} )} = \overline{{W}^{s} (\widetilde {Q} )} $ and $\widetilde {f} $ restricted to $ \overline{{W}^{u} (\widetilde {Q} )} $ is invariant and topologically mixing. Each connected component of the complement of $ \overline{{W}^{u} (\widetilde {Q} )} $ is a disk with diameter uniformly bounded from above. If $f$ is transitive, then $ \overline{{W}^{u} (\widetilde {Q} )} = { \mathbb{R} }^{2} $ and $\widetilde {f} $ is topologically mixing in the whole plane.

We extend the classical notion of block structure for periodic orbits of interval maps to the setting of tree maps and study the algebraic properties of the Markov matrix of a periodic tree pattern having a block structure. We also prove a formula which relates the topological entropy of a pattern having a block structure with that of the underlying periodic pattern obtained by collapsing each block to a point, and characterize the structure of the zero entropy patterns in terms of block structures. Finally, we prove that an $n$-periodic pattern has zero (positive) entropy if and only if all $n$-periodic patterns obtained by considering the $k\mathrm{th} $ iterate of the map on the invariant set have zero (respectively, positive) entropy, for each $k$ relatively prime to $n$.

We obtain sharp estimates on the growth rate of stable commutator length on random (geodesic) words, and on random walks, in hyperbolic groups and groups acting non-degenerately on hyperbolic spaces. In either case, we show that with high probability stable commutator length of an element of length $n$ is of order $n/ \log n$. This establishes quantitative refinements of qualitative results of Bestvina and Fujiwara and others on the infinite dimensionality of two-dimensional bounded cohomology in groups acting suitably on hyperbolic spaces, in the sense that we can control the geometry of the unit balls in these normed vector spaces (or rather, in random subspaces of their normed duals). As a corollary of our methods, we show that an element obtained by random walk of length $n$ in a mapping class group cannot be written as a product of fewer than $O(n/ \log n)$ reducible elements, with probability going to $1$ as $n$ goes to infinity. We also show that the translation length on the complex of free factors of a random walk of length $n$ on the outer automorphism group of a free group grows linearly in $n$.

We prove a meromorphic integrability criterion for the geodesic flow of an algebraic manifold of the form ${z}^{p} - f({x}_{1} , \ldots , {x}_{n} )= 0$ with the induced metric of ${ \mathbb{C} }^{n+ 1} $ and $f$ a homogeneous rational function, using a parallel between the properties of such algebraic manifolds and homogeneous potentials. We then apply this criterion to the manifolds of the form $z= {\lambda }_{1} { x}_{1}^{k} + \cdots + {\lambda }_{n} { x}_{n}^{k} $, $k\in { \mathbb{Z} }^{+ } $, and ${x}^{n} {y}^{m} {z}^{l} = 1, n, m, l\in \mathbb{Z} $, and prove that their geodesic flow is not integrable except for some given exceptional cases.

We completely describe the weak closure of the powers of the Koopman operator associated with Chacon’s classical automorphism. We show that weak limits of these powers are the ortho-projector to constants and an explicit family of polynomials. As a consequence, we answer negatively the question of $\alpha $-weak mixing for Chacon’s automorphism.

In this paper, we study the maximal pattern complexity of infinite words up to Abelian equivalence. We compute a lower bound for the Abelian maximal pattern complexity of infinite words which are both recurrent and aperiodic by projection. We show that in the case of binary words, the bound is actually achieved and gives a characterization of recurrent aperiodic words.

Let $f: X~\dashrightarrow ~X$ be a dominant meromorphic self-map, where $X$ is a compact, connected complex manifold of dimension $n\gt 1$. Suppose that there is an embedded copy of ${ \mathbb{P} }^{1} $ that is invariant under $f$, with $f$ holomorphic and transversally superattracting with degree $a$ in some neighborhood. Suppose that $f$ restricted to this line is given by $z\mapsto {z}^{b} $, with resulting invariant circle $S$. We prove that if $a\geq b$, then the local stable manifold ${ \mathcal{W} }_{\mathrm{loc} }^{s} (S)$ is real analytic. In fact, we state and prove a suitable localized version that can be useful in wider contexts. We then show that the condition $a\geq b$ cannot be relaxed without adding additional hypotheses by presenting two examples with $a\lt b$ for which ${ \mathcal{W} }_{\mathrm{loc} }^{s} (S)$ is not real analytic in the neighborhood of any point.

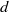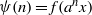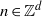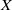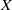A ($d$-parameter) basic nilsequence is a sequence of the form $\psi (n)= f({a}^{n} x)$,$n\in { \mathbb{Z} }^{d} $, where $x$ is a point of a compact nilmanifold $X$, $a$ is a translation on $X$, and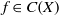$f\in C(X)$; a nilsequence is a uniform limit of basic nilsequences. If 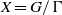$X= G/ \Gamma $ is a compact nilmanifold, 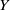$Y$ is a subnilmanifold of 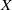$X$, 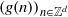$\mathop{(g(n))}\nolimits_{n\in { \mathbb{Z} }^{d} } $ is a polynomial sequence in 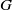$G$, and 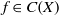$f\in C(X)$, we show that the sequence 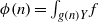$\phi (n)= \int \nolimits \nolimits_{g(n)Y} f$ is the sum of a basic nilsequence and a sequence that converges to zero in uniform density (a null-sequence). We also show that an integral of a family of nilsequences is a nilsequence plus a null-sequence. We deduce that for any invertible finite measure preserving system 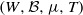$(W, \mathcal{B} , \mu , T)$, polynomials 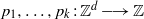${p}_{1} , \ldots , {p}_{k} : { \mathbb{Z} }^{d} \longrightarrow \mathbb{Z} $, and sets 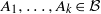${A}_{1} , \ldots , {A}_{k} \in \mathcal{B} $, the sequence 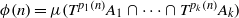$\phi (n)= \mu ({T}^{{p}_{1} (n)} {A}_{1} \cap \cdots \cap {T}^{{p}_{k} (n)} {A}_{k} )$, 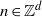$n\in { \mathbb{Z} }^{d} $, is the sum of a nilsequence and a null-sequence.

For $r\geq 3$, $p\geq 2$, we classify all actions of the groups ${ \mathrm{Diff} }_{c}^{r} ( \mathbb{R} )$ and ${ \mathrm{Diff} }_{+ }^{r} ({S}^{1} )$ by ${C}^{p} $-diffeomorphisms on the line and on the circle. This is the same as describing all non-trivial group homomorphisms between groups of compactly supported diffeomorphisms on 1-manifolds. We show that all such actions have an elementary form, which we call topologically diagonal. As an application, we answer a question of Ghys in the 1-manifold case: if $M$ is any closed manifold, and ${\mathrm{Diff} }^{\infty } \hspace{-2.0pt} \mathop{(M)}\nolimits_{0} $ injects into the diffeomorphism group of a 1-manifold, must $M$ be one-dimensional? We show that the answer is yes, even under more general conditions. Several lemmas on subgroups of diffeomorphism groups are of independent interest, including results on commuting subgroups and flows.

Variational monotone recurrence relations arise in solid state physics as generalizations of the Frenkel–Kontorova model for a ferromagnetic crystal. For such problems, Aubry–Mather theory establishes the existence of ‘ground states’ or ‘global minimizers’ of arbitrary rotation number. A nearest neighbor crystal model is equivalent to a Hamiltonian twist map. In this case, the global minimizers have a special property: they can only cross once. As a non-trivial consequence, every one of them has the Birkhoff property. In crystals with a larger range of interaction and for higher order recurrence relations, the single crossing property does not hold and there can exist global minimizers that are not Birkhoff. In this paper we investigate the crossings of global minimizers. Under a strong twist condition, we prove the following dichotomy: they are either Birkhoff, and thus very regular, or extremely irregular and non-physical: they then grow exponentially and oscillate. For Birkhoff minimizers, we also prove certain strong ordering properties that are well known for twist maps.

We prove a sharp large deviation principle concerning intervals shrinking with sub-exponential speed for certain models involving the Poincaré map related to a Markov family for an Axiom A flow restricted to a basic set $\Lambda $ satisfying some additional regularity assumptions.

In this paper we provide a complete modulus of analytic classification for germs of generic analytic families of diffeomorphisms which unfold a parabolic fixed point of codimension $k$. We start by showing that a generic family can be ‘prepared’, i.e. brought to a prenormal form ${f}_{\epsilon } (z)$ in which the multi-parameter $\epsilon $ is almost canonical (up to an action of $ \mathbb{Z} / k \mathbb{Z} $). As in the codimension one case treated in P. Mardešić, R. Roussarie and C. Rousseau [Modulus of analytic classification for unfoldings of generic parabolic diffeomorphisms. Mosc. Math. J. 4 (2004), 455–498], we show that the Ecalle–Voronin modulus can be unfolded to give a complete modulus for such germs. For this purpose, we define unfolded sectors in $z$-space that constitute natural domains on which the map ${f}_{\epsilon } $ can be brought to normal form in an almost unique way. The comparison of these normalizing changes of coordinates on the different sectors forms the analytic part of the modulus. This construction is performed on sectors in the multi-parameter space $\epsilon $ such that the closure of their union provides a neighborhood of the origin in parameter space.

Abért and Weiss have shown that the Bernoulli shift ${s}_{\Gamma } $ of a countably infinite group $\Gamma $ is weakly contained in any free measure preserving action $\boldsymbol{a}$ of $\Gamma $. Proving a conjecture of Ioana, we establish a strong version of this result by showing that ${\boldsymbol{s}}_{\Gamma } \times \boldsymbol{a}$ is weakly equivalent to $\boldsymbol{a}$. Using random Bernoulli shifts introduced by Abért, Glasner, and Virag, we generalize this to non-free actions, replacing ${\boldsymbol{s}}_{\Gamma } $ with a random Bernoulli shift associated to an invariant random subgroup, and replacing the product action with a relatively independent joining. The result for free actions is used along with the theory of Borel reducibility and Hjorth’s theory of turbulence to show that, on the weak equivalence class of a free measure preserving action, the equivalence relations of isomorphism, weak isomorphism, and unitary equivalence are not classifiable by countable structures. This in particular shows that there are no free weakly rigid actions, that is, actions whose weak equivalence class and isomorphism class coincide, answering negatively a question of Abért and Elek. We also answer a question of Kechris regarding two ergodic theoretic properties of residually finite groups. A countably infinite residually finite group $\Gamma $ is said to have property ${\text{EMD} }^{\ast } $ if the action ${\boldsymbol{p}}_{\Gamma } $ of $\Gamma $ on its profinite completion weakly contains all ergodic measure preserving actions of $\Gamma $, and $\Gamma $ is said to have property $\text{MD} $ if $\boldsymbol{\iota} \times {\boldsymbol{p}}_{\Gamma } $ weakly contains all measure preserving actions of $\Gamma $, where $\boldsymbol{\iota} $ denotes the identity action on a standard non-atomic probability space. Kechris has shown that ${\text{EMD} }^{\ast } $ implies $\text{MD} $ and asked if the two properties are actually equivalent. We provide a positive answer to this question by studying the relationship between convexity and weak containment in the space of measure preserving actions.