Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T04:34:39.195Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak equivalence and non-classifiability of measure preserving actions

Published online by Cambridge University Press:  13 August 2013

ROBIN D. TUCKER-DROB
ROBIN D. TUCKER-DROB*
Affiliation:
Department of Mathematics, California Institute of Technology, Pasadena, CA 91125, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Abért and Weiss have shown that the Bernoulli shift 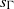${s}_{\Gamma } $ of a countably infinite group 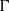$\Gamma $ is weakly contained in any free measure preserving action $\boldsymbol{a}$ of 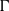$\Gamma $. Proving a conjecture of Ioana, we establish a strong version of this result by showing that 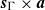${\boldsymbol{s}}_{\Gamma } \times \boldsymbol{a}$ is weakly equivalent to $\boldsymbol{a}$. Using random Bernoulli shifts introduced by Abért, Glasner, and Virag, we generalize this to non-free actions, replacing 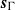${\boldsymbol{s}}_{\Gamma } $ with a random Bernoulli shift associated to an invariant random subgroup, and replacing the product action with a relatively independent joining. The result for free actions is used along with the theory of Borel reducibility and Hjorth’s theory of turbulence to show that, on the weak equivalence class of a free measure preserving action, the equivalence relations of isomorphism, weak isomorphism, and unitary equivalence are not classifiable by countable structures. This in particular shows that there are no free weakly rigid actions, that is, actions whose weak equivalence class and isomorphism class coincide, answering negatively a question of Abért and Elek. We also answer a question of Kechris regarding two ergodic theoretic properties of residually finite groups. A countably infinite residually finite group 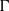$\Gamma $ is said to have property 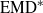${\text{EMD} }^{\ast } $ if the action 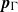${\boldsymbol{p}}_{\Gamma } $ of 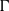$\Gamma $ on its profinite completion weakly contains all ergodic measure preserving actions of 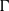$\Gamma $, and 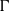$\Gamma $ is said to have property 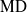$\text{MD} $ if 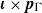$\boldsymbol{\iota} \times {\boldsymbol{p}}_{\Gamma } $ weakly contains all measure preserving actions of 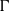$\Gamma $, where $\boldsymbol{\iota} $ denotes the identity action on a standard non-atomic probability space. Kechris has shown that 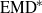${\text{EMD} }^{\ast } $ implies 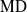$\text{MD} $ and asked if the two properties are actually equivalent. We provide a positive answer to this question by studying the relationship between convexity and weak containment in the space of measure preserving actions.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 1 , February 2015 , pp. 293 - 336
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abért, M. and Elek, G.. The space of actions, partition metric, and combinatorial rigidity. Preprint, arXiv:1108.2147v1.Google Scholar
Abért, M. and Elek, G.. Dynamical properties of profinite actions. Ergod. Th. & Dynam. Sys. 32 (2012), 1805–1835.CrossRefGoogle Scholar
Abért, M., Glasner, Y. and Virag, B.. Kesten’s theorem for invariant random subgroups. Preprint, arXiv:1201.3399v1.Google Scholar
Abért, M. and Weiss, B.. Bernoulli actions are weakly contained in any free action. Ergod. Th. & Dynam. Sys. 33 (2) (2013), 323–333.CrossRefGoogle Scholar
Bekka, B., de la Harpe, P. and Valette, A.. Kazhdan’s Property (T) (New Mathematical Monographs, 11). Cambridge University Press, Cambridge, 2008.Google Scholar
Bowen, L.. Periodicity and circle packings of the hyperbolic plane. Geom. Dedicata 102 (2003), 213–236.CrossRefGoogle Scholar
Bowen, L.. Random walks on coset spaces with applications to Furstenberg entropy. Preprint, arXiv:1008.4933v1.Google Scholar
Bowen, L. and Tucker-Drob, R.. On a co-induction question of Kechris. Israel J. Math. 194 (1) (2013), 209–224.Google Scholar
Conley, C., Kechris, A. and Tucker-Drob, R.. Ultraproducts of measure preserving actions and graph combinatorics. Ergod. Th. & Dynam. Sys. 33 (2) (2013), 334–374.CrossRefGoogle Scholar
Conley, C. and Kechris, A.. Measurable chromatic and independence numbers for ergodic graphs and group actions. Groups Geom. Dyn. 7 (1) (2013), 127–180.Google Scholar
Dixmier, J.. C*-algebras (North-Holland Mathematical Library, 15). North-Holland, Amsterdam, 1977.Google Scholar
Elek, G.. Finite graphs and amenability. Preprint, arXiv:1204.0449v1.Google Scholar
Elek, G. and Szegedy, B.. Limits of hypergraphs, removal and regularity lemmas. A non-standard approach. Preprint, arXiv:0705.2179v1.Google Scholar
Foreman, M. and Weiss, B.. An anti-classification theorem for ergodic measure preserving transformations. J. Eur. Math. Soc. 6 (3) (2004), 277–292.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003.Google Scholar
Hjorth, G.. Non-smooth infinite dimensional group representations. Preprint, 1997, (www.math.ucla.edu/~greg/research.html).Google Scholar
Hjorth, G.. Classification and Orbit Equivalence Relations (Mathematical Surveys and Monographs, 75). American Mathematical Society, Providence, RI, 2000.Google Scholar
Hjorth, G. and Kechris, A.. Analytic equivalence relations and Ulm-type classifications. J. Symbolic Logic 60 (4) (1995), 1273–1300.CrossRefGoogle Scholar
Kechris, A.. Classical Descriptive Set Theory (Graduate Texts in Mathematics, 156). Springer, New York, 1995.Google Scholar
Kechris, A.. Unitary representations and modular actions. J. Math. Sci. (N.Y.) 140 (3) (2007), 398–425.Google Scholar
Kechris, A.. Global Aspects of Ergodic Group Actions (Mathematical Surveys and Monographs, 160). American Mathematical Society, Providence, RI, 2010.CrossRefGoogle Scholar
Kechris, A.. Weak containment in the space of actions of a free group. Israel J. Math. 189 (1) (2012), 461–507.CrossRefGoogle Scholar
Kechris, A. and Tsankov, T.. Amenable actions and almost invariant sets. Proc. Amer. Math. Soc. 136 (2) (2008), 687–697.Google Scholar
Kerr, D., Li, H. and Pichot, M.. Turbulence, representations, and trace-preserving actions. Proc. Lond. Math. Soc. (3) 100 (2) (2010), 459–484.CrossRefGoogle Scholar
Moore, C. C.. Group extensions and cohomology for locally compact groups. III. Trans. Amer. Math. Soc. 221 (1) (1976), 1–33.Google Scholar
Ornstein, D. and Weiss, B.. Ergodic theory of amenable group actions. I. The Rohlin lemma. Bull. Amer. Math. Soc. (N.S.) 2 (1) (1980), 161–164.Google Scholar
Phelps, R.. Lectures on Choquet’s Theorem (Lecture Notes in Mathematics, 1757), 2nd edn. Springer, Berlin, 2001.Google Scholar
Vershik, A.. Totally nonfree actions and infinite symmetric group. Preprint, arXiv:1109.3413v4.Google Scholar
Zimmer, R. J.. Ergodic Theory and Semisimple Groups (Monographs in Mathematics, 81). Birkhäuser, Basel, 1984.Google Scholar