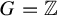1 Introduction
1.1 Definitions and results
Let
![]() $(X,\mathcal {B}, \mu )$
be a standard Lebesgue space and let T be a free, ergodic,
$(X,\mathcal {B}, \mu )$
be a standard Lebesgue space and let T be a free, ergodic,
![]() $\mu $
-preserving action of a discrete amenable group G on X. It is natural to ask what properties of T are preserved by a generic extension
$\mu $
-preserving action of a discrete amenable group G on X. It is natural to ask what properties of T are preserved by a generic extension
![]() $( \overline {X}, \overline {\mu }, \overline {T} )$
(a precise definition of ‘generic extension’ is discussed in §3). For example, it was shown in [Reference Glasner, Thouvenot and WeissGTW21] that a generic
$( \overline {X}, \overline {\mu }, \overline {T} )$
(a precise definition of ‘generic extension’ is discussed in §3). For example, it was shown in [Reference Glasner, Thouvenot and WeissGTW21] that a generic
![]() $\overline {T}$
has the same entropy as T and that if T is a non-trivial Bernoulli shift, then a generic
$\overline {T}$
has the same entropy as T and that if T is a non-trivial Bernoulli shift, then a generic
![]() $\overline {T}$
is also Bernoulli. A system
$\overline {T}$
is also Bernoulli. A system
![]() $(X, \mu , T)$
is said to be dominant if it is isomorphic to a generic extension
$(X, \mu , T)$
is said to be dominant if it is isomorphic to a generic extension
![]() $(\overline {X}, \overline {\mu }, \overline {T})$
. Thus, for example, the aforementioned results from [Reference Glasner, Thouvenot and WeissGTW21] together with Ornstein’s famous isomorphism theorem [Reference OrnsteinOrn70] imply that all non-trivial Bernoulli shifts are dominant. More generally, it has been shown in [Reference Austin, Glasner, Thouvenot and WeissAGTW21] that:
$(\overline {X}, \overline {\mu }, \overline {T})$
. Thus, for example, the aforementioned results from [Reference Glasner, Thouvenot and WeissGTW21] together with Ornstein’s famous isomorphism theorem [Reference OrnsteinOrn70] imply that all non-trivial Bernoulli shifts are dominant. More generally, it has been shown in [Reference Austin, Glasner, Thouvenot and WeissAGTW21] that:
-
(1) if
 $G = \mathbb {Z}$
, then
$G = \mathbb {Z}$
, then
 $(X,\mu ,T)$
is dominant if and only if it has positive Kolmogorov–Sinai entropy; and
$(X,\mu ,T)$
is dominant if and only if it has positive Kolmogorov–Sinai entropy; and -
(2) for any G, if
 $(X, \mu , T)$
has positive entropy, then it is dominant.
$(X, \mu , T)$
has positive entropy, then it is dominant.
In this paper, we complete the picture by proving the following result.
Theorem 1.1. Let G be any discrete amenable group and let
![]() $(X, \mu , T)$
be any free ergodic action with zero entropy. Then
$(X, \mu , T)$
be any free ergodic action with zero entropy. Then
![]() $(X, \mu , T)$
is not dominant.
$(X, \mu , T)$
is not dominant.
The proof of result (2) is based on the theory of ‘slow entropy’ developed by Katok and Thouvenot in [Reference Katok and ThouvenotKT97] (see also [Reference FerencziFer97]), and our proof of Theorem 1.1 uses the same ideas.
2 Slow entropy
Fix a Følner sequence
![]() $(F_n)$
for G. For
$(F_n)$
for G. For
![]() $g \in G$
, write
$g \in G$
, write
![]() $T^g x$
for the action of g on the point
$T^g x$
for the action of g on the point
![]() $x \in X$
, and for a subset
$x \in X$
, and for a subset
![]() $F \subseteq G$
, write
$F \subseteq G$
, write
![]() $T^F x = \{T^f x : f \in F \}$
. If
$T^F x = \{T^f x : f \in F \}$
. If
![]() $Q = \{Q_1, \ldots , Q_k\}$
is a partition of X, then for
$Q = \{Q_1, \ldots , Q_k\}$
is a partition of X, then for
![]() $x \in X$
denote by
$x \in X$
denote by
![]() $Q(x)$
the index of the cell of Q containing x. Sometimes we use the same notation to mean the cell itself; which meaning is intended will be clear from the context. Given a finite subset
$Q(x)$
the index of the cell of Q containing x. Sometimes we use the same notation to mean the cell itself; which meaning is intended will be clear from the context. Given a finite subset
![]() $F \subseteq G$
, the
$F \subseteq G$
, the
![]() ${(Q,F)}$
-name of x for the action T is the tuple
${(Q,F)}$
-name of x for the action T is the tuple
![]() $Q_{T,F}(x) := (Q(T^f x))_{f \in F} \in \{1,2,\ldots ,k\}^F$
. Similarly, we also define the partition
$Q_{T,F}(x) := (Q(T^f x))_{f \in F} \in \{1,2,\ldots ,k\}^F$
. Similarly, we also define the partition
![]() $Q_{T,F} := \bigvee _{f \in F} T^{f^{-1}} Q$
, and in some contexts we use the same notation
$Q_{T,F} := \bigvee _{f \in F} T^{f^{-1}} Q$
, and in some contexts we use the same notation
![]() $Q_{T,F}(x)$
to refer to the cell of
$Q_{T,F}(x)$
to refer to the cell of
![]() $Q_{T,F}$
containing x.
$Q_{T,F}$
containing x.
For a finite subset
![]() $F \subseteq G$
and any finite alphabet
$F \subseteq G$
and any finite alphabet
![]() $\Lambda $
, the symbolic space
$\Lambda $
, the symbolic space
![]() $\Lambda ^F$
is equipped with the normalized Hamming distance
$\Lambda ^F$
is equipped with the normalized Hamming distance
![]() $d_F(w,w') = ({1}/{|F|}) \sum _{f \in F} 1_{w(f) \neq w'(f)}$
.
$d_F(w,w') = ({1}/{|F|}) \sum _{f \in F} 1_{w(f) \neq w'(f)}$
.
Definition 2.1. Given a partition
![]() $Q = \{Q_1, \ldots , Q_k\}$
, a finite set
$Q = \{Q_1, \ldots , Q_k\}$
, a finite set
![]() $F \subseteq G$
, and
$F \subseteq G$
, and
![]() $\epsilon> 0$
, define
$\epsilon> 0$
, define
We refer to this set as the ‘
![]() $(Q,T,F)$
-Hamming ball of radius
$(Q,T,F)$
-Hamming ball of radius
![]() $\epsilon $
centered at x’. Formally, it is the preimage under the map
$\epsilon $
centered at x’. Formally, it is the preimage under the map
![]() $Q_{T,F}$
of the ball of radius
$Q_{T,F}$
of the ball of radius
![]() $\epsilon $
centered at
$\epsilon $
centered at
![]() $Q_{T,F}(x)$
in the metric space
$Q_{T,F}(x)$
in the metric space
![]() $([k]^F, d_F)$
.
$([k]^F, d_F)$
.
Definition 2.2. Given
![]() $\epsilon> 0$
, the Hamming
$\epsilon> 0$
, the Hamming
![]() $\epsilon $
-covering number of
$\epsilon $
-covering number of
![]() $\mu $
is defined to be the minimum number of
$\mu $
is defined to be the minimum number of
![]() $(Q,T,F)$
-Hamming balls of radius
$(Q,T,F)$
-Hamming balls of radius
![]() $\epsilon $
required to cover a subset of X of
$\epsilon $
required to cover a subset of X of
![]() $\mu $
-measure at least
$\mu $
-measure at least
![]() $1-\epsilon $
, and is denoted by
$1-\epsilon $
, and is denoted by
![]() $\operatorname {\mathrm {cov}}(Q,T,F,\mu ,\epsilon )$
.
$\operatorname {\mathrm {cov}}(Q,T,F,\mu ,\epsilon )$
.
Lemma 2.3. Let
![]() $\varphi : (X,T,\mu ) \to (Y, S, \nu )$
be an isomorphism. Also let Q be a finite partition of X, let F be a finite subset of G, and let
$\varphi : (X,T,\mu ) \to (Y, S, \nu )$
be an isomorphism. Also let Q be a finite partition of X, let F be a finite subset of G, and let
![]() $\epsilon> 0$
. Then
$\epsilon> 0$
. Then
![]() $\operatorname {\mathrm {cov}}(Q,T,F,\mu ,\epsilon ) = \operatorname {\mathrm {cov}}(\varphi Q, S, F, \nu , \epsilon )$
.
$\operatorname {\mathrm {cov}}(Q,T,F,\mu ,\epsilon ) = \operatorname {\mathrm {cov}}(\varphi Q, S, F, \nu , \epsilon )$
.
Proof. It is immediate from the definition of isomorphism that for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() ${x,x' \in X}$
,
${x,x' \in X}$
,
Therefore, it follows that
![]() $\varphi ( B_{\operatorname {Ham}}(Q,T,F,x,\epsilon ) ) = B_{\operatorname {Ham}}(\varphi Q, S, F, \varphi x, \epsilon )$
for
$\varphi ( B_{\operatorname {Ham}}(Q,T,F,x,\epsilon ) ) = B_{\operatorname {Ham}}(\varphi Q, S, F, \varphi x, \epsilon )$
for
![]() $\mu $
-almost every x. Thus, any collection of
$\mu $
-almost every x. Thus, any collection of
![]() $(Q,T,F)$
-Hamming balls in X covering a set of
$(Q,T,F)$
-Hamming balls in X covering a set of
![]() $\mu $
-measure
$\mu $
-measure
![]() $1-\epsilon $
is directly mapped by
$1-\epsilon $
is directly mapped by
![]() $\varphi $
to a collection of
$\varphi $
to a collection of
![]() $(\varphi Q, S, F)$
-Hamming balls in Y covering a set of
$(\varphi Q, S, F)$
-Hamming balls in Y covering a set of
![]() $\nu $
-measure
$\nu $
-measure
![]() $1-\epsilon $
. Therefore,
$1-\epsilon $
. Therefore,
![]() $\operatorname {\mathrm {cov}}(Q,T,F,\mu ,\epsilon ) \geq \operatorname {\mathrm {cov}}(\varphi Q, S, F, \nu , \epsilon )$
. The reverse inequality holds by doing the same argument with
$\operatorname {\mathrm {cov}}(Q,T,F,\mu ,\epsilon ) \geq \operatorname {\mathrm {cov}}(\varphi Q, S, F, \nu , \epsilon )$
. The reverse inequality holds by doing the same argument with
![]() $\varphi ^{-1}$
in place of
$\varphi ^{-1}$
in place of
![]() $\varphi $
.
$\varphi $
.
The goal of the rest of this section is to show that for a given action
![]() $(X,T,\mu )$
, the sequence of covering numbers
$(X,T,\mu )$
, the sequence of covering numbers
![]() $\operatorname {\mathrm {cov}}(Q, T, F_n, \mu , \epsilon )$
grows at a rate that is bounded uniformly for any choice of partition Q. A key ingredient is an analog of the classical Shannon–McMillan theorem for actions of amenable groups [Reference OllagnierMO85, Theorem 4.4.2].
$\operatorname {\mathrm {cov}}(Q, T, F_n, \mu , \epsilon )$
grows at a rate that is bounded uniformly for any choice of partition Q. A key ingredient is an analog of the classical Shannon–McMillan theorem for actions of amenable groups [Reference OllagnierMO85, Theorem 4.4.2].
Theorem 2.4. Let G be a countable amenable group and let
![]() $(F_n)$
be any Følner sequence for G. Let
$(F_n)$
be any Følner sequence for G. Let
![]() $(X,T,\mu )$
be an ergodic action of G and let Q be any finite partition of X. Then
$(X,T,\mu )$
be an ergodic action of G and let Q be any finite partition of X. Then
where h denotes the entropy. In particular, for any fixed
![]() $\gamma> 0$
,
$\gamma> 0$
,
Lemma 2.5. For any partition P, any Følner sequence
![]() $(F_n)$
and any
$(F_n)$
and any
![]() $\epsilon> 0$
, let
$\epsilon> 0$
, let
![]() $\ell (T, P, \mu , n, \epsilon )$
be the minimum number of
$\ell (T, P, \mu , n, \epsilon )$
be the minimum number of
![]() $P_{T, F_n}$
-cells required to cover a subset of X of measure more than
$P_{T, F_n}$
-cells required to cover a subset of X of measure more than
![]() $ 1-\epsilon $
. Then
$ 1-\epsilon $
. Then
Proof. Let
![]() $h = h(\mu , T, P)$
. Let
$h = h(\mu , T, P)$
. Let
![]() $\gamma> 0$
. By Theorem 2.4, for n sufficiently large depending on
$\gamma> 0$
. By Theorem 2.4, for n sufficiently large depending on
![]() $\gamma $
, we have
$\gamma $
, we have
Let
![]() $X'$
denote the set in the above equation. Let
$X'$
denote the set in the above equation. Let
![]() $\mathcal {G}$
be the family of cells of the partition
$\mathcal {G}$
be the family of cells of the partition
![]() $P_{T, F_n}$
that meet
$P_{T, F_n}$
that meet
![]() $X'$
. Then clearly
$X'$
. Then clearly
![]() $\mu ( \bigcup \mathcal {G} )> 1-\epsilon $
and
$\mu ( \bigcup \mathcal {G} )> 1-\epsilon $
and
![]() $|\mathcal {G}| < \exp ((h+\gamma ) |F_n|)$
. Therefore,
$|\mathcal {G}| < \exp ((h+\gamma ) |F_n|)$
. Therefore,
and this holds for arbitrary
![]() $\gamma $
, so we are done.
$\gamma $
, so we are done.
At this point, fix for all time
![]() $\epsilon = 1/100$
. We can also now omit
$\epsilon = 1/100$
. We can also now omit
![]() $\epsilon $
from all of the notation defined previously, because it will never change. In addition, assume from now on that the system
$\epsilon $
from all of the notation defined previously, because it will never change. In addition, assume from now on that the system
![]() $(X, T, \mu )$
has zero entropy.
$(X, T, \mu )$
has zero entropy.
Lemma 2.6. If
![]() $(F_n)$
is a Følner sequence for G and A is any finite subset of G, then
$(F_n)$
is a Følner sequence for G and A is any finite subset of G, then
![]() $(AF_n)$
is also a Følner sequence for G.
$(AF_n)$
is also a Følner sequence for G.
Proof. First, because A is finite and
![]() $(F_n)$
is Følner we have
$(F_n)$
is Følner we have
Now fix any
![]() $g \in G$
and observe that
$g \in G$
and observe that
which shows that
![]() $(AF_n)$
is a Følner sequence.
$(AF_n)$
is a Følner sequence.
Lemma 2.7. Let
![]() $b(m,n) \geq 0$
be real numbers satisfying:
$b(m,n) \geq 0$
be real numbers satisfying:
-
•
 $\lim _{n \to \infty } b(m,n) = 0$
for each fixed m; and
$\lim _{n \to \infty } b(m,n) = 0$
for each fixed m; and -
•
 $b(m+1, n) \geq b(m,n)$
for all
$b(m+1, n) \geq b(m,n)$
for all
 $m,n$
.
$m,n$
.
Then there exists a sequence
![]() $(a_n)$
such that
$(a_n)$
such that
![]() $a_n \to 0$
and for each fixed m,
$a_n \to 0$
and for each fixed m,
![]() $b(m,n) \leq a_n$
for n sufficiently large (depending on m).
$b(m,n) \leq a_n$
for n sufficiently large (depending on m).
Proof. For each m, let
![]() $N_m$
be such that
$N_m$
be such that
![]() $b(m,n) < 1/m$
for all
$b(m,n) < 1/m$
for all
![]() $n> N_m$
. Without loss of generality, we may assume that
$n> N_m$
. Without loss of generality, we may assume that
![]() $N_m < N_{m+1}$
. Then we define the sequence
$N_m < N_{m+1}$
. Then we define the sequence
![]() $(a_n)$
by
$(a_n)$
by
![]() ${a_n = b(1,n)}$
for
${a_n = b(1,n)}$
for
![]() $n \leq N_2$
and
$n \leq N_2$
and
![]() $a_n = b(m,n)$
for
$a_n = b(m,n)$
for
![]() $N_m < n \leq N_{m+1}$
. We have
$N_m < n \leq N_{m+1}$
. We have
![]() $a_n \to 0$
because
$a_n \to 0$
because
![]() ${a_n < 1/m}$
for all
${a_n < 1/m}$
for all
![]() $n> N_m$
. Finally, the fact that
$n> N_m$
. Finally, the fact that
![]() $b(m+1, n) \geq b(m,n)$
implies that for every fixed m,
$b(m+1, n) \geq b(m,n)$
implies that for every fixed m,
![]() $a_n \geq b(m,n)$
as soon as
$a_n \geq b(m,n)$
as soon as
![]() $n> N_m$
.
$n> N_m$
.
Proposition 2.8. There is a sequence
![]() $(a_n)$
such that:
$(a_n)$
such that:
-
(1)
 $\limsup _{n \to \infty } ({1}/{|F_n|}) \log a_n = 0$
; and
$\limsup _{n \to \infty } ({1}/{|F_n|}) \log a_n = 0$
; and -
(2) for any finite partition Q, there exists an N such that
 $\operatorname {\mathrm {cov}}(Q,T,F_n, \mu ) \leq a_n$
for all
$\operatorname {\mathrm {cov}}(Q,T,F_n, \mu ) \leq a_n$
for all
 $n> N$
.
$n> N$
.
Proof. Because T has zero entropy, there exists a finite generating partition for T (see, for example, [Reference SewardSew19, Corollary 1.2] or [Reference RosenthalRos88, Theorem 2
![]() ${}^{\prime }$
]). Fix such a partition P and let
${}^{\prime }$
]). Fix such a partition P and let
![]() $Q = \{Q_1, \ldots , Q_r\}$
be any given partition. Because P is generating, there is an integer m and another partition
$Q = \{Q_1, \ldots , Q_r\}$
be any given partition. Because P is generating, there is an integer m and another partition
![]() $Q' = \{Q^{\prime }_1, \ldots , Q^{\prime }_r \}$
such that
$Q' = \{Q^{\prime }_1, \ldots , Q^{\prime }_r \}$
such that
![]() $Q'$
is refined by
$Q'$
is refined by
![]() $P_{T, F_m}$
and
$P_{T, F_m}$
and
By the mean ergodic theorem, we can write
 $$ \begin{align*} &d_{F_n}(Q_{T, F_n}(x), Q^{\prime}_{T, F_n}(x)) \\&\quad= \frac{1}{|F_n|} \sum_{f \in F_n} 1_{\{ y : Q(y) \neq Q'(y) \}}(T^f x) \xrightarrow{L^1(\mu)} \mu \{ y : Q(y) \neq Q'(y) \} < \frac{\epsilon}{4}, \end{align*} $$
$$ \begin{align*} &d_{F_n}(Q_{T, F_n}(x), Q^{\prime}_{T, F_n}(x)) \\&\quad= \frac{1}{|F_n|} \sum_{f \in F_n} 1_{\{ y : Q(y) \neq Q'(y) \}}(T^f x) \xrightarrow{L^1(\mu)} \mu \{ y : Q(y) \neq Q'(y) \} < \frac{\epsilon}{4}, \end{align*} $$
so, in particular, for n sufficiently large, we have
Let Y denote the set
![]() $\{ x : d_{F_n}(Q_{T, F_n}(x), Q^{\prime }_{T, F_n}(x)) < \epsilon /2 \}$
.
$\{ x : d_{F_n}(Q_{T, F_n}(x), Q^{\prime }_{T, F_n}(x)) < \epsilon /2 \}$
.
Recall that
![]() $Q'$
is refined by
$Q'$
is refined by
![]() $P_{T, F_m}$
, so
$P_{T, F_m}$
, so
![]() $Q^{\prime }_{T, F_n}$
is refined by
$Q^{\prime }_{T, F_n}$
is refined by
![]() $(P_{T, F_m})_{T, F_n} = P_{T, F_m F_n}$
. Let
$(P_{T, F_m})_{T, F_n} = P_{T, F_m F_n}$
. Let
![]() $\ell = \ell (m,n)$
be the minimum number of
$\ell = \ell (m,n)$
be the minimum number of
![]() $P_{T, F_m F_n}$
cells required to cover a set of
$P_{T, F_m F_n}$
cells required to cover a set of
![]() $\mu $
-measure at least
$\mu $
-measure at least
![]() $1-\epsilon /4$
, and let
$1-\epsilon /4$
, and let
![]() $C_1, \ldots , C_{\ell }$
be such a collection of cells satisfying
$C_1, \ldots , C_{\ell }$
be such a collection of cells satisfying
![]() $\mu ( \bigcup _i C_i ) \geq 1 - \epsilon /4$
. If any of the
$\mu ( \bigcup _i C_i ) \geq 1 - \epsilon /4$
. If any of the
![]() $C_i$
do not meet the set Y, then drop them from the list. Because
$C_i$
do not meet the set Y, then drop them from the list. Because
![]() $\mu (Y)> 1- \epsilon /4$
we can still assume after dropping that
$\mu (Y)> 1- \epsilon /4$
we can still assume after dropping that
![]() $\mu ( \bigcup _i C_i )> 1 - \epsilon /2$
. Choose a set of representatives
$\mu ( \bigcup _i C_i )> 1 - \epsilon /2$
. Choose a set of representatives
![]() $y_1, \ldots y_{\ell }$
with each
$y_1, \ldots y_{\ell }$
with each
![]() $y_i \in C_i \cap Y$
.
$y_i \in C_i \cap Y$
.
Now we claim that
![]() $Y \cap \bigcup _i C_i \subseteq \bigcup _{i=1}^{\ell } B_{\operatorname {Ham}}(Q, T, F_n, y_i, \epsilon )$
. To see this, let
$Y \cap \bigcup _i C_i \subseteq \bigcup _{i=1}^{\ell } B_{\operatorname {Ham}}(Q, T, F_n, y_i, \epsilon )$
. To see this, let
![]() $x \in Y \cap \bigcup _i C_i$
. Then there is one index j such that x and
$x \in Y \cap \bigcup _i C_i$
. Then there is one index j such that x and
![]() $y_j$
are in the same cell of
$y_j$
are in the same cell of
![]() $P_{T, F_mF_n}$
. We can then estimate
$P_{T, F_mF_n}$
. We can then estimate
 $$ \begin{align*} d_{F_n}( Q_{T, F_n}(x), Q_{T, F_n}(y_j) ) &\leq d_{F_n}( Q_{T, F_n}(x), Q^{\prime}_{T, F_n}(x) ) + d_{F_n}( Q^{\prime}_{T, F_n}(x), Q^{\prime}_{T, F_n}(y_j) )\\&\quad + d_{F_n}( Q^{\prime}_{T, F_n}(y_j), Q_{T, F_n}(y_j) ) \\&< \frac{\epsilon}{2} + 0 + \frac{\epsilon}{2} = \epsilon. \end{align*} $$
$$ \begin{align*} d_{F_n}( Q_{T, F_n}(x), Q_{T, F_n}(y_j) ) &\leq d_{F_n}( Q_{T, F_n}(x), Q^{\prime}_{T, F_n}(x) ) + d_{F_n}( Q^{\prime}_{T, F_n}(x), Q^{\prime}_{T, F_n}(y_j) )\\&\quad + d_{F_n}( Q^{\prime}_{T, F_n}(y_j), Q_{T, F_n}(y_j) ) \\&< \frac{\epsilon}{2} + 0 + \frac{\epsilon}{2} = \epsilon. \end{align*} $$
The bounds for the first and third terms come from the fact that
![]() $x, y_j \in Y$
. The second term is
$x, y_j \in Y$
. The second term is
![]() $0$
because
$0$
because
![]() $Q^{\prime }_{F_n}$
is refined by
$Q^{\prime }_{F_n}$
is refined by
![]() $P_{T, F_m F_n}$
and
$P_{T, F_m F_n}$
and
![]() $y_j$
was chosen so that x and
$y_j$
was chosen so that x and
![]() $y_j$
are in the same
$y_j$
are in the same
![]() $P_{T, F_m F_n}$
-cell. Therefore,
$P_{T, F_m F_n}$
-cell. Therefore,
![]() $\operatorname {\mathrm {cov}}(Q, T, F_n, \mu ) \leq \ell (m,n)$
. Thus, the proof is complete once we find a fixed sequence
$\operatorname {\mathrm {cov}}(Q, T, F_n, \mu ) \leq \ell (m,n)$
. Thus, the proof is complete once we find a fixed sequence
![]() $(a_n)$
that is subexponential in
$(a_n)$
that is subexponential in
![]() $|F_n|$
and eventually dominates
$|F_n|$
and eventually dominates
![]() $\ell (m,n)$
for each fixed m.
$\ell (m,n)$
for each fixed m.
Because T has zero entropy, Lemmas 2.5 and 2.6 imply that
Note also that because
![]() $P_{T, F_{m+1}F_n}$
refines
$P_{T, F_{m+1}F_n}$
refines
![]() $P_{T, F_m F_n}$
, we have
$P_{T, F_m F_n}$
, we have
![]() $\ell (m+1, n) \geq \ell (m,n)$
for all
$\ell (m+1, n) \geq \ell (m,n)$
for all
![]() $m,n$
. Therefore, we can apply Lemma 2.7 to the numbers
$m,n$
. Therefore, we can apply Lemma 2.7 to the numbers
![]() $b(m,n) = |F_n|^{-1} \log \ell (m,n)$
to produce a sequence
$b(m,n) = |F_n|^{-1} \log \ell (m,n)$
to produce a sequence
![]() $(a_n')$
satisfying
$(a_n')$
satisfying
![]() $a_n' \to 0$
and
$a_n' \to 0$
and
![]() $a_n' \geq b(m,n)$
eventually for each fixed m. Then
$a_n' \geq b(m,n)$
eventually for each fixed m. Then
![]() $a_n := \exp (|F_n| a_n')$
is the desired sequence.
$a_n := \exp (|F_n| a_n')$
is the desired sequence.
3 Cocycles and extensions
Let I be the unit interval
![]() $[0,1]$
and let m be Lebesgue measure on I. Denote by
$[0,1]$
and let m be Lebesgue measure on I. Denote by
![]() $\operatorname {\mathrm {Aut}}(I,m)$
the group of invertible m-preserving transformations of I. A cocycle on X is a family of measurable maps
$\operatorname {\mathrm {Aut}}(I,m)$
the group of invertible m-preserving transformations of I. A cocycle on X is a family of measurable maps
![]() $\alpha _g : X \to \operatorname {\mathrm {Aut}}(I,m)$
indexed by
$\alpha _g : X \to \operatorname {\mathrm {Aut}}(I,m)$
indexed by
![]() $g \in G$
that satisfies the cocycle condition: for every
$g \in G$
that satisfies the cocycle condition: for every
![]() $g,h \in G$
and
$g,h \in G$
and
![]() $\mu $
-almost every x,
$\mu $
-almost every x,
![]() $\alpha _{hg}(x) = \alpha _h(T^g x) \circ \alpha _g(x)$
. A cocycle can equivalently be thought of as a measurable map
$\alpha _{hg}(x) = \alpha _h(T^g x) \circ \alpha _g(x)$
. A cocycle can equivalently be thought of as a measurable map
![]() $\alpha : R \to \operatorname {\mathrm {Aut}}(I,m)$
, where
$\alpha : R \to \operatorname {\mathrm {Aut}}(I,m)$
, where
![]() ${R \subseteq X \times X}$
is the orbit equivalence relation induced by T (that is,
${R \subseteq X \times X}$
is the orbit equivalence relation induced by T (that is,
![]() $(x,y) \in R$
if and only if
$(x,y) \in R$
if and only if
![]() $y = T^g x$
for some
$y = T^g x$
for some
![]() $g \in G$
). With this perspective, the cocycle condition takes the form
$g \in G$
). With this perspective, the cocycle condition takes the form
![]() $\alpha (x,z) = \alpha (y,z) \circ \alpha (x,y)$
. A cocycle
$\alpha (x,z) = \alpha (y,z) \circ \alpha (x,y)$
. A cocycle
![]() $\alpha $
induces the skew product action
$\alpha $
induces the skew product action
![]() $T_{\alpha }$
of G on the larger space
$T_{\alpha }$
of G on the larger space
![]() $X \times I$
defined by
$X \times I$
defined by
This action preserves the measure
![]() $\mu \times m$
and is an extension of the original action
$\mu \times m$
and is an extension of the original action
![]() $(X,T,\mu )$
.
$(X,T,\mu )$
.
By a classical theorem of Rokhlin (see, for example, [Reference GlasnerGla03, Theorem 3.18]), any infinite-to-one ergodic extension of
![]() $(X,\mu ,T)$
is isomorphic to
$(X,\mu ,T)$
is isomorphic to
![]() $T_{\alpha }$
for some cocycle
$T_{\alpha }$
for some cocycle
![]() $\alpha $
. Therefore, by topologizing the space of all cocycles on X we can capture the notion of a ‘generic’ extension: a property is said to hold for a generic extension if it holds for a dense
$\alpha $
. Therefore, by topologizing the space of all cocycles on X we can capture the notion of a ‘generic’ extension: a property is said to hold for a generic extension if it holds for a dense
![]() $G_{\delta }$
set of cocycles. Denote the space of all cocycles on X by
$G_{\delta }$
set of cocycles. Denote the space of all cocycles on X by
![]() $\operatorname {Co}(X)$
. Topologizing
$\operatorname {Co}(X)$
. Topologizing
![]() $\operatorname {Co}(X)$
is done in a few stages.
$\operatorname {Co}(X)$
is done in a few stages.
-
(1) Let
 $\mathcal {B}(I)$
be the Borel sets in I and let
$\mathcal {B}(I)$
be the Borel sets in I and let
 $(E_n)$
be a sequence in
$(E_n)$
be a sequence in
 $\mathcal {B}(I)$
that is dense in the
$\mathcal {B}(I)$
that is dense in the
 $m ( \cdot \,\triangle \, \cdot )$
metric. For example,
$m ( \cdot \,\triangle \, \cdot )$
metric. For example,
 $(E_n)$
could be an enumeration of the family of all finite unions of intervals with rational endpoints.
$(E_n)$
could be an enumeration of the family of all finite unions of intervals with rational endpoints. -
(2) The group
 $\operatorname {\mathrm {Aut}}(I,m)$
is completely metrizable via the metric
$\operatorname {\mathrm {Aut}}(I,m)$
is completely metrizable via the metric  $$ \begin{align*} d_A(\phi, \psi) = \frac12 \sum_{n \geq 1} 2^{-n} [m (\phi E_n \,\triangle\, \psi E_n) + m(\phi^{-1} E_n \,\triangle\, \psi^{-1} E_n)]. \end{align*} $$
$$ \begin{align*} d_A(\phi, \psi) = \frac12 \sum_{n \geq 1} 2^{-n} [m (\phi E_n \,\triangle\, \psi E_n) + m(\phi^{-1} E_n \,\triangle\, \psi^{-1} E_n)]. \end{align*} $$
Note that with this metric,
 $\operatorname {\mathrm {Aut}}(I,m)$
has diameter at most
$\operatorname {\mathrm {Aut}}(I,m)$
has diameter at most
 $1$
. See, for example, [Reference KechrisKec10, §1.1]
$1$
. See, for example, [Reference KechrisKec10, §1.1] -
(3) If
 $\alpha _0, \beta _0$
are maps
$\alpha _0, \beta _0$
are maps
 $X \to \operatorname {\mathrm {Aut}}(I,m)$
, then define
$X \to \operatorname {\mathrm {Aut}}(I,m)$
, then define
 $\operatorname {\mathrm {dist}}(\alpha _0, \beta _0) = \int d_A(\alpha _0(x), \beta _0(x))\, d\mu (x)$
.
$\operatorname {\mathrm {dist}}(\alpha _0, \beta _0) = \int d_A(\alpha _0(x), \beta _0(x))\, d\mu (x)$
. -
(4) The metric defined in the previous step induces a topology on
 $\operatorname {\mathrm {Aut}}(I,m)^X$
. Therefore, because
$\operatorname {\mathrm {Aut}}(I,m)^X$
. Therefore, because
 $\operatorname {Co}(X)$
is just a certain (closed) subset of
$\operatorname {Co}(X)$
is just a certain (closed) subset of
 $(\operatorname {\mathrm {Aut}}(I,m)^X)^G$
, it just inherits the product topology.
$(\operatorname {\mathrm {Aut}}(I,m)^X)^G$
, it just inherits the product topology.
To summarize, if
![]() $\alpha $
is a cocycle, then a basic open neighborhood
$\alpha $
is a cocycle, then a basic open neighborhood
![]() $\alpha $
is specified by two parameters: a finite subset
$\alpha $
is specified by two parameters: a finite subset
![]() $F \subseteq G$
and
$F \subseteq G$
and
![]() $\eta> 0$
. The
$\eta> 0$
. The
![]() $(F,\eta )$
-neighborhood of
$(F,\eta )$
-neighborhood of
![]() $\alpha $
is
$\alpha $
is
![]() ${\{ \beta \in \operatorname {Co}(X): \operatorname {\mathrm {dist}}(\alpha _g, \beta _g) < \eta \text { for all } g \in F \}}$
. In practice, we always arrange things so that there is a set of x of measure at least
${\{ \beta \in \operatorname {Co}(X): \operatorname {\mathrm {dist}}(\alpha _g, \beta _g) < \eta \text { for all } g \in F \}}$
. In practice, we always arrange things so that there is a set of x of measure at least
![]() $ 1-\eta $
on which
$ 1-\eta $
on which
![]() $\alpha _g(x) = \beta _g(x)$
for all
$\alpha _g(x) = \beta _g(x)$
for all
![]() $g \in F$
, which is sufficient to guarantee that
$g \in F$
, which is sufficient to guarantee that
![]() $\beta $
is in the
$\beta $
is in the
![]() $(F,\eta )$
-neighborhood of
$(F,\eta )$
-neighborhood of
![]() $\alpha $
.
$\alpha $
.
Let
![]() $\overline {Q}$
be the partition
$\overline {Q}$
be the partition
![]() $\{X \times [0,1/2], X \times (1/2, 1] \}$
of
$\{X \times [0,1/2], X \times (1/2, 1] \}$
of
![]() $X \times I$
. We derive Theorem 1.1 from the following result about covering numbers of extensions, which is the main technical result of the paper.
$X \times I$
. We derive Theorem 1.1 from the following result about covering numbers of extensions, which is the main technical result of the paper.
Theorem 3.1. For any sequence
![]() $(a_n)$
satisfying
$(a_n)$
satisfying
![]() $\limsup _{n \to \infty } ({1}/{|F_n|}) \log a_n = 0$
, there is a dense
$\limsup _{n \to \infty } ({1}/{|F_n|}) \log a_n = 0$
, there is a dense
![]() $G_{\delta }$
set
$G_{\delta }$
set
![]() $\mathcal {U} \subseteq \operatorname {Co}(X)$
such that for any
$\mathcal {U} \subseteq \operatorname {Co}(X)$
such that for any
![]() $\alpha \in \mathcal {U}$
,
$\alpha \in \mathcal {U}$
,
![]() $\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m)> a_n$
for infinitely many n.
$\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m)> a_n$
for infinitely many n.
Proof that Theorem 3.1 implies Theorem 1.1
Choose a sequence
![]() $(a_n)$
as in Proposition 2.8 such that for any partition Q,
$(a_n)$
as in Proposition 2.8 such that for any partition Q,
![]() $\operatorname {\mathrm {cov}}(Q, T, F_n, \mu ) \leq a_n$
for sufficiently large n. Let
$\operatorname {\mathrm {cov}}(Q, T, F_n, \mu ) \leq a_n$
for sufficiently large n. Let
![]() $\mathcal {U}$
be the dense
$\mathcal {U}$
be the dense
![]() $G_{\delta }$
set of cocycles associated to
$G_{\delta }$
set of cocycles associated to
![]() $(a_n)$
as guaranteed by Theorem 3.1 and let
$(a_n)$
as guaranteed by Theorem 3.1 and let
![]() ${\alpha \in \mathcal {U}}$
, so we know that
${\alpha \in \mathcal {U}}$
, so we know that
![]() $\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m)> a_n$
for infinitely many n. Now if
$\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m)> a_n$
for infinitely many n. Now if
![]() $\varphi : (X \times I, T_{\alpha }, \mu \times m) \to (X, T, \mu )$
were an isomorphism, then by Lemma 2.3,
$\varphi : (X \times I, T_{\alpha }, \mu \times m) \to (X, T, \mu )$
were an isomorphism, then by Lemma 2.3,
![]() $\varphi \overline {Q}$
would be a partition of X satisfying
$\varphi \overline {Q}$
would be a partition of X satisfying
![]() $\operatorname {\mathrm {cov}}(\varphi \overline {Q}, T, F_n, \mu ) = \operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m)> a_n$
for infinitely many n, contradicting the conclusion of Proposition 2.8. Therefore, we have produced a dense
$\operatorname {\mathrm {cov}}(\varphi \overline {Q}, T, F_n, \mu ) = \operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m)> a_n$
for infinitely many n, contradicting the conclusion of Proposition 2.8. Therefore, we have produced a dense
![]() $G_{\delta }$
set of cocycles
$G_{\delta }$
set of cocycles
![]() $\alpha $
such that
$\alpha $
such that
![]() $T_{\alpha } \not \simeq T$
, which implies Theorem 1.1.
$T_{\alpha } \not \simeq T$
, which implies Theorem 1.1.
To prove Theorem 3.1, we need to show roughly that
![]() $\{ \alpha \in \operatorname {Co}(X) : \operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m) \text { is large} \}$
is both open and dense. We address the open part here and leave the density part until the next section. Let
$\{ \alpha \in \operatorname {Co}(X) : \operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m) \text { is large} \}$
is both open and dense. We address the open part here and leave the density part until the next section. Let
![]() $\pi $
be the partition
$\pi $
be the partition
![]() $\{[0,1/2), [1/2, 1]\}$
of I.
$\{[0,1/2), [1/2, 1]\}$
of I.
Lemma 3.2. If
![]() $\beta ^{(n)}$
is a sequence of cocycles converging to
$\beta ^{(n)}$
is a sequence of cocycles converging to
![]() $\alpha $
, then for any finite
$\alpha $
, then for any finite
![]() $F \subseteq G$
, we have
$F \subseteq G$
, we have
Proof. For the names
![]() $\overline {Q}_{T_{\beta ^{(n)}}, F}(x,t)$
and
$\overline {Q}_{T_{\beta ^{(n)}}, F}(x,t)$
and
![]() $\overline {Q}_{T_{\alpha }, F}(x,t)$
to be the same means that for every
$\overline {Q}_{T_{\alpha }, F}(x,t)$
to be the same means that for every
![]() $g \in F$
,
$g \in F$
,
which is equivalent to
The idea is the following. For fixed g and x, if
![]() $\alpha _g(x)$
and
$\alpha _g(x)$
and
![]() $\beta ^{(n)}_g(x)$
are close in
$\beta ^{(n)}_g(x)$
are close in
![]() $d_A$
, then (1) fails for only a small measure set of t. In addition, if
$d_A$
, then (1) fails for only a small measure set of t. In addition, if
![]() $\beta ^{(n)}$
is very close to
$\beta ^{(n)}$
is very close to
![]() $\alpha $
in the cocycle topology, then
$\alpha $
in the cocycle topology, then
![]() $\beta ^{(n)}_g(x)$
and
$\beta ^{(n)}_g(x)$
and
![]() $\alpha _g(x)$
are close for all
$\alpha _g(x)$
are close for all
![]() $g \in F$
and most
$g \in F$
and most
![]() $x \in X$
. Then, by Fubini’s theorem, we will get that the measure of the set of
$x \in X$
. Then, by Fubini’s theorem, we will get that the measure of the set of
![]() $(x,t)$
failing (1) is small.
$(x,t)$
failing (1) is small.
Here are the details. Fix
![]() $\rho> 0$
; we show that the measure of the desired set is at least
$\rho> 0$
; we show that the measure of the desired set is at least
![]() $1-\rho $
for n sufficiently large. First, let
$1-\rho $
for n sufficiently large. First, let
![]() $\sigma $
be so small that for any
$\sigma $
be so small that for any
![]() $\phi , \psi \in \operatorname {\mathrm {Aut}}(I,m)$
,
$\phi , \psi \in \operatorname {\mathrm {Aut}}(I,m)$
,
This is possible because
Then, from the definition of the cocycle topology, we have
Let n be large enough so that the above is larger than
![]() $1-\rho /2$
. Then, by Fubini’s theorem, we have
$1-\rho /2$
. Then, by Fubini’s theorem, we have
 $$ \begin{align*} &(\mu \times m) \{ (x,t) : \overline{Q}_{T_{\beta^{(n)}}, F}(x,t) = \overline{Q}_{T_{\alpha}, F}(x,t) \} \\&\quad= \int m \{ t : \pi( \beta^{(n)}_g(x) t ) = \pi ( \alpha_g(x) t ) \text{ for all } g \in F \} \,d\mu(x). \end{align*} $$
$$ \begin{align*} &(\mu \times m) \{ (x,t) : \overline{Q}_{T_{\beta^{(n)}}, F}(x,t) = \overline{Q}_{T_{\alpha}, F}(x,t) \} \\&\quad= \int m \{ t : \pi( \beta^{(n)}_g(x) t ) = \pi ( \alpha_g(x) t ) \text{ for all } g \in F \} \,d\mu(x). \end{align*} $$
We have arranged things so that the integrand above is greater than
![]() $1-\rho /2$
on a set of x of
$1-\rho /2$
on a set of x of
![]() $\mu $
-measure greater than
$\mu $
-measure greater than
![]() $ 1-\rho /2$
, so the integral is at least
$ 1-\rho /2$
, so the integral is at least
![]() $(1-\rho /2)(1-\rho /2)> 1-\rho $
as desired.
$(1-\rho /2)(1-\rho /2)> 1-\rho $
as desired.
Lemma 3.3. For any finite
![]() $F \subseteq G$
and any
$F \subseteq G$
and any
![]() $L> 0$
, the set
$L> 0$
, the set
![]() $\{ \alpha \in \operatorname {Co}(X) : \operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F, \mu \times m)> L \}$
is open in
$\{ \alpha \in \operatorname {Co}(X) : \operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F, \mu \times m)> L \}$
is open in
![]() $\operatorname {Co}(X)$
.
$\operatorname {Co}(X)$
.
Proof. Suppose
![]() $\beta ^{(n)}$
is a sequence of cocycles converging to
$\beta ^{(n)}$
is a sequence of cocycles converging to
![]() $\alpha $
and satisfying
$\alpha $
and satisfying
![]() $\operatorname {\mathrm {cov}}(\overline {Q}, T_{\beta ^{(n)}}, F, \mu \times m) \leq L$
for all n. We show that
$\operatorname {\mathrm {cov}}(\overline {Q}, T_{\beta ^{(n)}}, F, \mu \times m) \leq L$
for all n. We show that
![]() $\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F, \mu \times m) \leq L$
as well. The covering number
$\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F, \mu \times m) \leq L$
as well. The covering number
![]() $\operatorname {\mathrm {cov}}(\overline {Q}, T_{\beta ^{(n)}}, F, \mu \times m)$
is a quantity which really depends only on the measure
$\operatorname {\mathrm {cov}}(\overline {Q}, T_{\beta ^{(n)}}, F, \mu \times m)$
is a quantity which really depends only on the measure
![]() $( \overline {Q}_{T_{\beta ^{(n)}} , F} )_* (\mu \times m) \in \operatorname {\mathrm {Prob}} ( \{0,1\}^F )$
, which we now call
$( \overline {Q}_{T_{\beta ^{(n)}} , F} )_* (\mu \times m) \in \operatorname {\mathrm {Prob}} ( \{0,1\}^F )$
, which we now call
![]() $\nu _n$
for short. The assumption that
$\nu _n$
for short. The assumption that
![]() $\operatorname {\mathrm {cov}}(\overline {Q}, T_{\beta ^{(n)}}, F, \mu \times m) \leq L$
for all n says that for each n, there is a collection of L words
$\operatorname {\mathrm {cov}}(\overline {Q}, T_{\beta ^{(n)}}, F, \mu \times m) \leq L$
for all n says that for each n, there is a collection of L words
![]() $w_1^{(n)}, \ldots , w_L^{(n)} \in \{0,1\}^F$
such that the Hamming balls of radius
$w_1^{(n)}, \ldots , w_L^{(n)} \in \{0,1\}^F$
such that the Hamming balls of radius
![]() $\epsilon $
centered at these words cover a set of
$\epsilon $
centered at these words cover a set of
![]() $\nu _n$
-measure at least
$\nu _n$
-measure at least
![]() $1-\epsilon $
. As
$1-\epsilon $
. As
![]() $\{0,1\}^F$
is a finite set, there are only finitely many possibilities for the collection
$\{0,1\}^F$
is a finite set, there are only finitely many possibilities for the collection
![]() $( w_1^{(n)}, \ldots , w_L^{(n)} )$
. Therefore, by passing to a subsequence and relabeling, we may assume that there is a fixed collection of words
$( w_1^{(n)}, \ldots , w_L^{(n)} )$
. Therefore, by passing to a subsequence and relabeling, we may assume that there is a fixed collection of words
![]() $w_1, \ldots , w_L$
with the property that if we let
$w_1, \ldots , w_L$
with the property that if we let
![]() $B_i$
be the Hamming ball of radius
$B_i$
be the Hamming ball of radius
![]() $\epsilon $
centered at
$\epsilon $
centered at
![]() $w_i$
, then
$w_i$
, then
![]() $\nu _n ( \bigcup _{i=1}^L B_i ) \geq 1-\epsilon $
for every n.
$\nu _n ( \bigcup _{i=1}^L B_i ) \geq 1-\epsilon $
for every n.
Now, by Lemma 3.2, the map
![]() $\overline {Q}_{T_{\beta ^{(n)}} , F}$
agrees with
$\overline {Q}_{T_{\beta ^{(n)}} , F}$
agrees with
![]() $\overline {Q}_{T_{\alpha } , F}$
on a set of measure converging to
$\overline {Q}_{T_{\alpha } , F}$
on a set of measure converging to
![]() $1$
as
$1$
as
![]() $n \to \infty $
. This implies that the measures
$n \to \infty $
. This implies that the measures
![]() $\nu _n$
converge in the total variation norm on
$\nu _n$
converge in the total variation norm on
![]() $\operatorname {\mathrm {Prob}} ( \{0,1\}^F )$
to
$\operatorname {\mathrm {Prob}} ( \{0,1\}^F )$
to
![]() $\nu := ( \overline {Q}_{T_{\alpha } , F} )_*(\mu \times m)$
. As
$\nu := ( \overline {Q}_{T_{\alpha } , F} )_*(\mu \times m)$
. As
![]() $\nu _n ( \bigcup _{i=1}^L B_i ) \geq 1-\epsilon $
for every n, we conclude that
$\nu _n ( \bigcup _{i=1}^L B_i ) \geq 1-\epsilon $
for every n, we conclude that
![]() $\nu ( \bigcup _{i=1}^L B_i ) \geq 1-\epsilon $
also, which implies that
$\nu ( \bigcup _{i=1}^L B_i ) \geq 1-\epsilon $
also, which implies that
![]() $\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F, \mu \times m) \leq L$
as desired.
$\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F, \mu \times m) \leq L$
as desired.
Define
![]() $\mathcal {U}_N := \{\alpha \in \operatorname {Co}(X) : \operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m)> a_n \text { for some } n > N \}$
. By Lemma 3.3, each
$\mathcal {U}_N := \{\alpha \in \operatorname {Co}(X) : \operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m)> a_n \text { for some } n > N \}$
. By Lemma 3.3, each
![]() $\mathcal {U}_N$
is a union of open sets and therefore open. In addition,
$\mathcal {U}_N$
is a union of open sets and therefore open. In addition,
![]() $\bigcap _{N} \mathcal {U}_N$
is exactly the set of
$\bigcap _{N} \mathcal {U}_N$
is exactly the set of
![]() $\alpha \in \operatorname {Co}(X)$
satisfying
$\alpha \in \operatorname {Co}(X)$
satisfying
![]() $\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m)> a_n$
infinitely often. Therefore, by the Baire category theorem, in order to prove Theorem 3.1 it suffices to prove
$\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m)> a_n$
infinitely often. Therefore, by the Baire category theorem, in order to prove Theorem 3.1 it suffices to prove
Proposition 3.4. For each N,
![]() $\mathcal {U}_N$
is dense in
$\mathcal {U}_N$
is dense in
![]() $\operatorname {Co}(X)$
.
$\operatorname {Co}(X)$
.
The proof of this proposition is the content of the next section.
4 Proof of Proposition 3.4
4.1 Setup
Let N be fixed and let
![]() $\alpha _0$
be an arbitrary cocycle. Consider a neighborhood of
$\alpha _0$
be an arbitrary cocycle. Consider a neighborhood of
![]() $\alpha _0$
determined by a finite set
$\alpha _0$
determined by a finite set
![]() $F \subseteq G$
and
$F \subseteq G$
and
![]() $\eta> 0$
. We can assume without loss of generality that
$\eta> 0$
. We can assume without loss of generality that
![]() $\eta \ll \epsilon = 1/100$
. We produce a new cocycle
$\eta \ll \epsilon = 1/100$
. We produce a new cocycle
![]() $\alpha \in \mathcal {U}_N$
such that there is a set
$\alpha \in \mathcal {U}_N$
such that there is a set
![]() $X'$
of measure at least
$X'$
of measure at least
![]() $1-\eta $
on which
$1-\eta $
on which
![]() $\alpha _f(x) = (\alpha _0)_f(x)$
for all
$\alpha _f(x) = (\alpha _0)_f(x)$
for all
![]() $f \in F$
, implying that
$f \in F$
, implying that
![]() $\alpha $
is in the
$\alpha $
is in the
![]() $(F,\eta )$
-neighborhood of
$(F,\eta )$
-neighborhood of
![]() $\alpha _0$
. The construction of such an
$\alpha _0$
. The construction of such an
![]() $\alpha $
is based on the fact that the orbit equivalence relation R is hyperfinite.
$\alpha $
is based on the fact that the orbit equivalence relation R is hyperfinite.
Theorem 4.1. [Reference Ornstein and WeissOW80, Theorem 6]
There is an increasing sequence of equivalence relations
![]() $R_n \subseteq X \times X$
such that:
$R_n \subseteq X \times X$
such that:
-
• each
 $R_n$
is measurable as a subset of
$R_n$
is measurable as a subset of
 $X \times X$
;
$X \times X$
; -
• every cell of every
 $R_n$
is finite; and
$R_n$
is finite; and -
•
 $\bigcup _n R_n$
agrees
$\bigcup _n R_n$
agrees
 $\mu $
-almost everywhere with R.
$\mu $
-almost everywhere with R.
Fix such a sequence
![]() $(R_n)$
and for
$(R_n)$
and for
![]() $x \in X$
, write
$x \in X$
, write
![]() $R_n(x)$
to denote the cell of
$R_n(x)$
to denote the cell of
![]() $R_n$
that contains x.
$R_n$
that contains x.
Lemma 4.2. There exists an
![]() $m_1$
such that
$m_1$
such that
![]() $\mu \{ x \in X : T^F x \subseteq R_{m_1}(x) \}> 1-\eta $
.
$\mu \{ x \in X : T^F x \subseteq R_{m_1}(x) \}> 1-\eta $
.
Proof. Almost every x satisfies
![]() $T^G x = \bigcup _{m} R_m(x)$
, so, in particular, for
$T^G x = \bigcup _{m} R_m(x)$
, so, in particular, for
![]() $\mu $
-almost every x, there is an
$\mu $
-almost every x, there is an
![]() $m_x$
such that
$m_x$
such that
![]() $T^F x \subseteq R_m(x)$
for all
$T^F x \subseteq R_m(x)$
for all
![]() $m \geq m_x$
. Letting
$m \geq m_x$
. Letting
![]() $X_{\ell } = \{x \in X : m_x \leq \ell \}$
, we see that the sets
$X_{\ell } = \{x \in X : m_x \leq \ell \}$
, we see that the sets
![]() $X_{\ell }$
are increasing and exhaust almost all of X. Therefore, we can pick
$X_{\ell }$
are increasing and exhaust almost all of X. Therefore, we can pick
![]() $m_1$
so that
$m_1$
so that
![]() $\mu (X_{m_1})> 1-\eta $
.
$\mu (X_{m_1})> 1-\eta $
.
Now we drop
![]() $R_1, \ldots , R_{m_1 - 1}$
from the sequence and assume that
$R_1, \ldots , R_{m_1 - 1}$
from the sequence and assume that
![]() $m_1 = 1$
.
$m_1 = 1$
.
Lemma 4.3. There exists a K such that
![]() $\mu \{x : |R_1(x)| \leq K \}> 1-\eta $
.
$\mu \{x : |R_1(x)| \leq K \}> 1-\eta $
.
Proof. Every
![]() $R_1$
-cell is finite, so if we define
$R_1$
-cell is finite, so if we define
![]() $X_k = \{x \in X : |R_1(x)| \leq k \}$
, then the
$X_k = \{x \in X : |R_1(x)| \leq k \}$
, then the
![]() $X_k$
are increasing and exhaust all of X. Thus, we pick K so that
$X_k$
are increasing and exhaust all of X. Thus, we pick K so that
![]() $\mu (X_K)> 1-\eta $
.
$\mu (X_K)> 1-\eta $
.
Continue to use the notation
![]() $X_K = \{x \in X : |R_1(x)| \leq K \}$
.
$X_K = \{x \in X : |R_1(x)| \leq K \}$
.
Lemma 4.4. For all n sufficiently large,
![]() $\mu \{x \in X : {|(T^{F_n} x) \cap X_K|}/{|F_n|}> 1-2\eta \} > 1-\eta $
.
$\mu \{x \in X : {|(T^{F_n} x) \cap X_K|}/{|F_n|}> 1-2\eta \} > 1-\eta $
.
Proof. We have
![]() $|(T^{F_n} x) \cap X_K| = \sum _{f \in F_n} 1_{X_K}(T^f x)$
. By the mean ergodic theorem [Reference GlasnerGla03, Theorem 3.33], we get
$|(T^{F_n} x) \cap X_K| = \sum _{f \in F_n} 1_{X_K}(T^f x)$
. By the mean ergodic theorem [Reference GlasnerGla03, Theorem 3.33], we get
 $$ \begin{align*} \frac{|(T^{F_n} x) \cap X_K|}{|F_n|} \to \mu(X_K)> 1-\eta \quad \text{in probability as } n \to \infty. \end{align*} $$
$$ \begin{align*} \frac{|(T^{F_n} x) \cap X_K|}{|F_n|} \to \mu(X_K)> 1-\eta \quad \text{in probability as } n \to \infty. \end{align*} $$
Therefore, in particular,
![]() $\mu \{ x \in X : {|(T^{F_n} x) \cap X_K|}/{|F_n|}> 1-2\eta \} \to 1$
as
$\mu \{ x \in X : {|(T^{F_n} x) \cap X_K|}/{|F_n|}> 1-2\eta \} \to 1$
as
![]() $n \to \infty $
, so this measure is greater than
$n \to \infty $
, so this measure is greater than
![]() $1-\eta $
for all n sufficiently large.
$1-\eta $
for all n sufficiently large.
From now on, let n be a fixed number that is large enough so that the above lemma holds,
![]() $n> N$
, and
$n> N$
, and
![]() $\tfrac 12 \exp ( {1}/{8K^2} \cdot |F_n| )> a_n$
. This is possible because
$\tfrac 12 \exp ( {1}/{8K^2} \cdot |F_n| )> a_n$
. This is possible because
![]() $(a_n)$
is assumed to be subexponential in
$(a_n)$
is assumed to be subexponential in
![]() $|F_n|$
. The relevance of the final condition will appear at the end.
$|F_n|$
. The relevance of the final condition will appear at the end.
Lemma 4.5. There is an
![]() $m_2$
such that
$m_2$
such that
![]() $\mu \{x \in X : T^{F_n} x \subseteq R_{m_2}(x) \}> 1-\eta $
.
$\mu \{x \in X : T^{F_n} x \subseteq R_{m_2}(x) \}> 1-\eta $
.
Proof. The proof follows the same lines as Lemma 4.2.
Again, drop
![]() $R_2, \ldots , R_{m_2-1}$
from the sequence of equivalence relations and assume
$R_2, \ldots , R_{m_2-1}$
from the sequence of equivalence relations and assume
![]() $m_2 = 2$
.
$m_2 = 2$
.
4.2 Construction of the perturbed cocycle
Let
![]() $(R_n)$
be the relabeled sequence of equivalence relations from the previous section. The following measure-theoretic fact is well known. Recall that two partitions P and
$(R_n)$
be the relabeled sequence of equivalence relations from the previous section. The following measure-theoretic fact is well known. Recall that two partitions P and
![]() $P'$
of I are said to be independent with respect to m if
$P'$
of I are said to be independent with respect to m if
![]() $m(E \cap E') = m(E)m(E')$
for any
$m(E \cap E') = m(E)m(E')$
for any
![]() $E \in P$
,
$E \in P$
,
![]() $E' \in P'$
.
$E' \in P'$
.
Lemma 4.6. Let P and
![]() $P'$
be two finite partitions of I. Then there exists a
$P'$
be two finite partitions of I. Then there exists a
![]() $\varphi \in \operatorname {\mathrm {Aut}}(I,m)$
such that P and
$\varphi \in \operatorname {\mathrm {Aut}}(I,m)$
such that P and
![]() $\varphi ^{-1}P'$
are independent with respect to m.
$\varphi ^{-1}P'$
are independent with respect to m.
Proposition 4.7. For any
![]() $\alpha _0 \in \operatorname {Co}(X)$
, there is an
$\alpha _0 \in \operatorname {Co}(X)$
, there is an
![]() $\alpha \in \operatorname {Co}(X)$
such that:
$\alpha \in \operatorname {Co}(X)$
such that:
-
(1)
 $\alpha _g(x) = (\alpha _0)_g(x)$
whenever
$\alpha _g(x) = (\alpha _0)_g(x)$
whenever
 $(x, T^g x) \in R_1$
; and
$(x, T^g x) \in R_1$
; and -
(2) for
 $\mu $
-almost every x, the following holds. If C is an
$\mu $
-almost every x, the following holds. If C is an
 $R_1$
-cell contained in
$R_1$
-cell contained in
 $R_2(x)$
, consider the map
$R_2(x)$
, consider the map
 $Y_C: t \mapsto \overline {Q}_{T_{\alpha }, \{g : T^g x \in C \}}(x,t)$
as a random variable on the underlying space
$Y_C: t \mapsto \overline {Q}_{T_{\alpha }, \{g : T^g x \in C \}}(x,t)$
as a random variable on the underlying space
 $(I,m)$
. Then as C ranges over all such
$(I,m)$
. Then as C ranges over all such
 $R_1$
-cells, the random variables
$R_1$
-cells, the random variables
 $Y_C$
are independent.
$Y_C$
are independent.
Proof. We give here only a sketch of the proof and leave the full details to Appendix A. It is more convenient to adopt the perspective of a cocycle as a map
![]() $\alpha : R \to \operatorname {\mathrm {Aut}}(I,m)$
satisfying the condition
$\alpha : R \to \operatorname {\mathrm {Aut}}(I,m)$
satisfying the condition
![]() $\alpha (x,z) = \alpha (y,z) \circ \alpha (x,y)$
.
$\alpha (x,z) = \alpha (y,z) \circ \alpha (x,y)$
.
Step 1. For
![]() $(x,y) \in R_1$
, let
$(x,y) \in R_1$
, let
![]() $\alpha (x,y) = \alpha _0(x,y)$
.
$\alpha (x,y) = \alpha _0(x,y)$
.
Step 2. Fix an
![]() $R_2$
-cell
$R_2$
-cell
![]() $\overline {C}$
. Enumerate by
$\overline {C}$
. Enumerate by
![]() $\{C_1, \ldots , C_k\}$
all of the
$\{C_1, \ldots , C_k\}$
all of the
![]() $R_1$
-cells contained in
$R_1$
-cells contained in
![]() $\overline {C}$
and choose from each a representative
$\overline {C}$
and choose from each a representative
![]() $x_i \in C_i$
.
$x_i \in C_i$
.
Step 3. Let
![]() $\pi $
denote the partition
$\pi $
denote the partition
![]() $\{[0,1/2), [1/2, 1]\}$
of I. Define
$\{[0,1/2), [1/2, 1]\}$
of I. Define
![]() $\alpha (x_1, x_2)$
to be an element of
$\alpha (x_1, x_2)$
to be an element of
![]() $\operatorname {\mathrm {Aut}}(I,m)$
such that
$\operatorname {\mathrm {Aut}}(I,m)$
such that
 $$ \begin{align*} \bigvee_{y \in C_1} \alpha(x_1, y)^{-1} \pi \quad \text{and} \quad \alpha(x_1, x_2)^{-1} \bigg(\bigvee_{y \in C_2} \alpha(x_2, y)^{-1} \pi \bigg) \end{align*} $$
$$ \begin{align*} \bigvee_{y \in C_1} \alpha(x_1, y)^{-1} \pi \quad \text{and} \quad \alpha(x_1, x_2)^{-1} \bigg(\bigvee_{y \in C_2} \alpha(x_2, y)^{-1} \pi \bigg) \end{align*} $$
are independent. These expressions are well defined because
![]() $\alpha $
has already been defined on
$\alpha $
has already been defined on
![]() $R_1$
and we use Lemma 4.6 to guarantee that such an element of
$R_1$
and we use Lemma 4.6 to guarantee that such an element of
![]() $\operatorname {\mathrm {Aut}}(I,m)$
exists.
$\operatorname {\mathrm {Aut}}(I,m)$
exists.
Step 4. There is now a unique way to extend the definition of
![]() $\alpha $
to
$\alpha $
to
![]() $(C_1 \cup C_2) \times (C_1 \cup C_2)$
that is consistent with the cocycle condition. For arbitrary
$(C_1 \cup C_2) \times (C_1 \cup C_2)$
that is consistent with the cocycle condition. For arbitrary
![]() $y_1 \in C_1, y_2 \in C_2$
, define
$y_1 \in C_1, y_2 \in C_2$
, define
 $$ \begin{align*} \alpha(y_1, y_2) &= \alpha(x_2, y_2) \circ \alpha(x_1, x_2) \circ \alpha(y_1, x_1) \quad \text{and}\\ \alpha(y_2, y_1) &= \alpha(y_1, y_2)^{-1}. \end{align*} $$
$$ \begin{align*} \alpha(y_1, y_2) &= \alpha(x_2, y_2) \circ \alpha(x_1, x_2) \circ \alpha(y_1, x_1) \quad \text{and}\\ \alpha(y_2, y_1) &= \alpha(y_1, y_2)^{-1}. \end{align*} $$
The middle term in the first equation was defined in the previous step and the outer two terms were defined in step 1.
Step 5. Extend the definition of
![]() $\alpha $
to the rest of the
$\alpha $
to the rest of the
![]() $C_i$
inductively, making each cell independent of all the previous ones. Suppose
$C_i$
inductively, making each cell independent of all the previous ones. Suppose
![]() $\alpha $
has been defined on
$\alpha $
has been defined on
![]() $( C_1 \cup \dots \cup C_j ) \times ( C_1 \cup \dots \cup C_j )$
. Using Lemma 4.6 again, define
$( C_1 \cup \dots \cup C_j ) \times ( C_1 \cup \dots \cup C_j )$
. Using Lemma 4.6 again, define
![]() $\alpha (x_1, x_{j+1})$
to be an element of
$\alpha (x_1, x_{j+1})$
to be an element of
![]() $\operatorname {\mathrm {Aut}}(I,m)$
such that
$\operatorname {\mathrm {Aut}}(I,m)$
such that
 $$ \begin{align*} \bigvee_{y \in C_1 \cup \dots \cup C_j} \alpha(x_1, y)^{-1}\pi \quad \text{and} \quad \alpha(x_1,x_{j+1})^{-1} \bigg( \bigvee_{y \in C_{j+1}} \alpha(x_{j+1}, y)^{-1}\pi \bigg) \end{align*} $$
$$ \begin{align*} \bigvee_{y \in C_1 \cup \dots \cup C_j} \alpha(x_1, y)^{-1}\pi \quad \text{and} \quad \alpha(x_1,x_{j+1})^{-1} \bigg( \bigvee_{y \in C_{j+1}} \alpha(x_{j+1}, y)^{-1}\pi \bigg) \end{align*} $$
are independent. Then, just as in step 4, there is a unique way to extend the definition of
![]() $\alpha $
to all of
$\alpha $
to all of
![]() $(C_1 \cup \dots \cup C_{j+1}) \times (C_1 \cup \dots \cup C_{j+1})$
. At the end of this process,
$(C_1 \cup \dots \cup C_{j+1}) \times (C_1 \cup \dots \cup C_{j+1})$
. At the end of this process,
![]() $\alpha $
has been defined on all of
$\alpha $
has been defined on all of
![]() $\overline {C} \times \overline {C}$
. This was done for an arbitrary
$\overline {C} \times \overline {C}$
. This was done for an arbitrary
![]() $R_2$
-cell
$R_2$
-cell
![]() $\overline {C}$
, so now
$\overline {C}$
, so now
![]() $\alpha $
is defined on
$\alpha $
is defined on
![]() $R_2$
.
$R_2$
.
Step 6. For each
![]() $N \geq 2$
, extend the definition of
$N \geq 2$
, extend the definition of
![]() $\alpha $
from
$\alpha $
from
![]() $R_N$
to
$R_N$
to
![]() $R_{N+1}$
with the same procedure, but there is no need to set up any independence. Instead, every time there is a choice for how to define
$R_{N+1}$
with the same procedure, but there is no need to set up any independence. Instead, every time there is a choice for how to define
![]() $\alpha $
between two of the cell representatives, just take it to be the identity. This defines
$\alpha $
between two of the cell representatives, just take it to be the identity. This defines
![]() $\alpha $
on
$\alpha $
on
![]() $\bigcup _{N \geq 1} R_N$
, which is equal mod
$\bigcup _{N \geq 1} R_N$
, which is equal mod
![]() $\mu $
to the full orbit equivalence relation, so
$\mu $
to the full orbit equivalence relation, so
![]() $\alpha $
is a well-defined cocycle.
$\alpha $
is a well-defined cocycle.
Now we verify the two claimed properties of
![]() $\alpha $
. Property (1) is immediate from step 1 of the construction. To check property (2), fix x and let
$\alpha $
. Property (1) is immediate from step 1 of the construction. To check property (2), fix x and let
![]() $C_j$
be any of the
$C_j$
be any of the
![]() $R_1$
-cells contained in
$R_1$
-cells contained in
![]() $R_2(x)$
. Note that the name
$R_2(x)$
. Note that the name
![]() $\overline {Q}_{T_{\alpha }, \{g : T^g x \in C_j\}}(x,t)$
records the data
$\overline {Q}_{T_{\alpha }, \{g : T^g x \in C_j\}}(x,t)$
records the data
![]() $\overline {Q}(T^g_{\alpha }(x,t)) = \overline {Q}(T^g x, \alpha _g(x) t) = \pi ( \alpha _g(x) t)$
for all g such that
$\overline {Q}(T^g_{\alpha }(x,t)) = \overline {Q}(T^g x, \alpha _g(x) t) = \pi ( \alpha _g(x) t)$
for all g such that
![]() $T^g x \in C_j$
, which, by switching to the other notation, is the same data as
$T^g x \in C_j$
, which, by switching to the other notation, is the same data as
![]() $\pi (\alpha (x, y) t)$
for
$\pi (\alpha (x, y) t)$
for
![]() $y \in C_j$
. Thus, the set of t for which
$y \in C_j$
. Thus, the set of t for which
![]() $\overline {Q}_{T_{\alpha }, \{g : T^g x \in C_j\}}(x,t)$
is equal to a particular word is given by a corresponding particular cell of the partition
$\overline {Q}_{T_{\alpha }, \{g : T^g x \in C_j\}}(x,t)$
is equal to a particular word is given by a corresponding particular cell of the partition
![]() $\bigvee _{y \in C_j} \alpha (x,y)^{-1} \pi = \alpha (x, x_1)^{-1} ( \bigvee _{y \in C_j} \alpha (x_1, y)^{-1} \pi )$
. The construction of
$\bigvee _{y \in C_j} \alpha (x,y)^{-1} \pi = \alpha (x, x_1)^{-1} ( \bigvee _{y \in C_j} \alpha (x_1, y)^{-1} \pi )$
. The construction of
![]() $\alpha $
was defined exactly so that the partitions
$\alpha $
was defined exactly so that the partitions
![]() $\bigvee _{y \in C_j} \alpha (x_1, y)^{-1} \pi $
are all independent and the names
$\bigvee _{y \in C_j} \alpha (x_1, y)^{-1} \pi $
are all independent and the names
![]() $\overline {Q}_{T_{\alpha }, \{g : T^g x \in _j\}}(x,t)$
are determined by these independent partitions pulled back by the fixed m-preserving map
$\overline {Q}_{T_{\alpha }, \{g : T^g x \in _j\}}(x,t)$
are determined by these independent partitions pulled back by the fixed m-preserving map
![]() $\alpha (x, x_1)$
, so they are also independent.
$\alpha (x, x_1)$
, so they are also independent.
The reason this is only a sketch is because it is not clear that the construction described here can be done in a way so that the resulting
![]() $\alpha $
is a measurable function. To do it properly requires a slightly different approach; see Appendix A for full details.
$\alpha $
is a measurable function. To do it properly requires a slightly different approach; see Appendix A for full details.
Letting
![]() $\widetilde {X} = \{x \in X : T^F x \subseteq R_1(x) \}$
, this construction guarantees that
$\widetilde {X} = \{x \in X : T^F x \subseteq R_1(x) \}$
, this construction guarantees that
![]() $\alpha _f(x) = (\alpha _0)_f(x)$
for all
$\alpha _f(x) = (\alpha _0)_f(x)$
for all
![]() $f \in F, x \in \widetilde {X}$
. By Lemma 4.2,
$f \in F, x \in \widetilde {X}$
. By Lemma 4.2,
![]() $\mu (\widetilde {X})> 1-\eta $
, so this shows that
$\mu (\widetilde {X})> 1-\eta $
, so this shows that
![]() $\alpha $
is in the
$\alpha $
is in the
![]() $(F,\eta )$
-neighborhood of
$(F,\eta )$
-neighborhood of
![]() $\alpha _0$
.
$\alpha _0$
.
4.3 Estimating the size of Hamming balls
Let
![]() $\alpha $
be the cocycle constructed in the previous section. We estimate the
$\alpha $
be the cocycle constructed in the previous section. We estimate the
![]() $(\mu \times m)$
-measure of
$(\mu \times m)$
-measure of
![]() $(\overline {Q}, T_{\alpha }, F_n)$
-Hamming balls in order to get a lower bound for the covering number. The following formulation of Hoeffding’s inequality will be quite useful [Reference VershyninVer18, Theorem 2.2.6].
$(\overline {Q}, T_{\alpha }, F_n)$
-Hamming balls in order to get a lower bound for the covering number. The following formulation of Hoeffding’s inequality will be quite useful [Reference VershyninVer18, Theorem 2.2.6].
Theorem 4.8. Let
![]() $Y_1, \ldots , Y_{\ell }$
be independent random variables such that each
$Y_1, \ldots , Y_{\ell }$
be independent random variables such that each
![]() ${Y_i \in [0,K]}$
almost surely. Let
${Y_i \in [0,K]}$
almost surely. Let
![]() $a = \mathbb {E} [ \sum Y_i ]$
. Then for any
$a = \mathbb {E} [ \sum Y_i ]$
. Then for any
![]() $t>0$
,
$t>0$
,
 $$ \begin{align*} \mathbb{P}\bigg( \sum_{i=1}^{\ell} Y_i < a - t \bigg) \leq \exp\bigg( - \frac{2t^2}{K^2 \ell} \bigg). \end{align*} $$
$$ \begin{align*} \mathbb{P}\bigg( \sum_{i=1}^{\ell} Y_i < a - t \bigg) \leq \exp\bigg( - \frac{2t^2}{K^2 \ell} \bigg). \end{align*} $$
Let
![]() $X_0 = \{x \in X : {|(T^{F_n} x) \cap X_K|}/{|F_n|}> 1-2\eta \text { and } T^{F_n} x \subseteq R_2(x) \}$
. By Lemmas 4.4 and 4.5,
$X_0 = \{x \in X : {|(T^{F_n} x) \cap X_K|}/{|F_n|}> 1-2\eta \text { and } T^{F_n} x \subseteq R_2(x) \}$
. By Lemmas 4.4 and 4.5,
![]() $\mu (X_0)> 1 - 2\eta $
. In addition, write
$\mu (X_0)> 1 - 2\eta $
. In addition, write
![]() $\mu \times m = \int m_x \,d\mu (x)$
, where
$\mu \times m = \int m_x \,d\mu (x)$
, where
![]() ${m_x = \delta _x \times m}$
.
${m_x = \delta _x \times m}$
.
Proposition 4.9. For any
![]() $(x,t) \in X_0 \times I$
,
$(x,t) \in X_0 \times I$
,
 $$ \begin{align} m_x( B_{\operatorname{Ham}}(\overline{Q}, T_{\alpha}, F_n, (x,t),\epsilon) ) \leq \exp\bigg( - \frac{1}{8K^2} \cdot |F_n| \bigg). \end{align} $$
$$ \begin{align} m_x( B_{\operatorname{Ham}}(\overline{Q}, T_{\alpha}, F_n, (x,t),\epsilon) ) \leq \exp\bigg( - \frac{1}{8K^2} \cdot |F_n| \bigg). \end{align} $$
Proof. Let
![]() $\mathcal {C}$
be the collection of
$\mathcal {C}$
be the collection of
![]() $R_1$
-cells C that meet
$R_1$
-cells C that meet
![]() $T^{F_n} x$
and satisfy
$T^{F_n} x$
and satisfy
![]() $|C| \leq K$
. For each
$|C| \leq K$
. For each
![]() $C \in \mathcal {C}$
, let
$C \in \mathcal {C}$
, let
![]() $F_C = \{f \in F_n : T^f x \in C \}$
. Define
$F_C = \{f \in F_n : T^f x \in C \}$
. Define
 $$ \begin{align*} Y(t') = |F_n| \cdot d_{F_n} ( \overline{Q}_{T_{\alpha}, F_n}(x,t), \overline{Q}_{T_{\alpha}, F_n}(x,t') ) = \sum_{f \in F_n} 1_{\overline{Q}(T_{\alpha}^f(x,t)) \neq \overline{Q}(T_{\alpha}^f(x,t'))}, \end{align*} $$
$$ \begin{align*} Y(t') = |F_n| \cdot d_{F_n} ( \overline{Q}_{T_{\alpha}, F_n}(x,t), \overline{Q}_{T_{\alpha}, F_n}(x,t') ) = \sum_{f \in F_n} 1_{\overline{Q}(T_{\alpha}^f(x,t)) \neq \overline{Q}(T_{\alpha}^f(x,t'))}, \end{align*} $$
and for each
![]() $C \in \mathcal {C}$
, define
$C \in \mathcal {C}$
, define
 $$ \begin{align*} Y_C(t') = \sum_{f \in F_C} 1_{\overline{Q}(T_{\alpha}^f(x,t)) \neq \overline{Q}(T_{\alpha}^f(x,t'))}. \end{align*} $$
$$ \begin{align*} Y_C(t') = \sum_{f \in F_C} 1_{\overline{Q}(T_{\alpha}^f(x,t)) \neq \overline{Q}(T_{\alpha}^f(x,t'))}. \end{align*} $$
Then we have
so to get an upper bound for
![]() $m_x ( B_{\operatorname {Ham}}(\overline {Q}, T_{\alpha }, F_n, (x,t),\epsilon ) ) = m \{ t' : Y(t') < \epsilon |F_n| \}$
, it is sufficient to control
$m_x ( B_{\operatorname {Ham}}(\overline {Q}, T_{\alpha }, F_n, (x,t),\epsilon ) ) = m \{ t' : Y(t') < \epsilon |F_n| \}$
, it is sufficient to control
![]() $m \{ t' : \sum _{C \in \mathcal {C}} Y_C(t') < \epsilon |F_n| \}$
.
$m \{ t' : \sum _{C \in \mathcal {C}} Y_C(t') < \epsilon |F_n| \}$
.
View each
![]() $Y_C(t')$
as a random variable on the underlying probability space
$Y_C(t')$
as a random variable on the underlying probability space
![]() $(I,m)$
. Our construction of the cocycle
$(I,m)$
. Our construction of the cocycle
![]() $\alpha $
guarantees that the collection of names
$\alpha $
guarantees that the collection of names
![]() $\overline {Q}_{T_{\alpha }, F_C}(x,t')$
as C ranges over all of the
$\overline {Q}_{T_{\alpha }, F_C}(x,t')$
as C ranges over all of the
![]() $R_1$
-cells contained in
$R_1$
-cells contained in
![]() $R_2(x)$
is an independent collection. Therefore, in particular, the
$R_2(x)$
is an independent collection. Therefore, in particular, the
![]() $Y_C$
for
$Y_C$
for
![]() $C \in \mathcal {C}$
are independent (the assumption that
$C \in \mathcal {C}$
are independent (the assumption that
![]() $x \in X_0$
guarantees that all
$x \in X_0$
guarantees that all
![]() $C \in \mathcal {C}$
are contained in
$C \in \mathcal {C}$
are contained in
![]() $R_2(x)$
).
$R_2(x)$
).
We also have that each
![]() $Y_C \in [0,K]$
and the expectation of the sum is
$Y_C \in [0,K]$
and the expectation of the sum is
 $$ \begin{align*} a &:= \sum_{C \in \mathcal{C}} \int Y_C(t') \,dm(t') = \sum_{C \in \mathcal{C}} \sum_{f \in F_C} \int 1_{\overline{Q}(T_{\alpha}^f(x,t)) \neq \overline{Q}(T_{\alpha}^f(x,t'))} \,dm(t') = \sum_{C \in \mathcal{C}} \frac{1}{2} |F_C| \\&= \frac12 \sum_{C \in \mathcal{C}}|C \cap (T^{F_n} x)|> \frac12 (1-2\eta)|F_n|, \end{align*} $$
$$ \begin{align*} a &:= \sum_{C \in \mathcal{C}} \int Y_C(t') \,dm(t') = \sum_{C \in \mathcal{C}} \sum_{f \in F_C} \int 1_{\overline{Q}(T_{\alpha}^f(x,t)) \neq \overline{Q}(T_{\alpha}^f(x,t'))} \,dm(t') = \sum_{C \in \mathcal{C}} \frac{1}{2} |F_C| \\&= \frac12 \sum_{C \in \mathcal{C}}|C \cap (T^{F_n} x)|> \frac12 (1-2\eta)|F_n|, \end{align*} $$
where the final inequality is true because
![]() $x \in X_0$
. Thus, we can apply Theorem 4.8 with
$x \in X_0$
. Thus, we can apply Theorem 4.8 with
![]() $t = a - \epsilon |F_n|$
to conclude
$t = a - \epsilon |F_n|$
to conclude
 $$ \begin{align*} m \bigg\{ t' : \sum_{C \in \mathcal{C}} Y_C(t') < \epsilon|F_n| \bigg\} &\leq \exp\bigg( \frac{-2t^2}{K^2 |\mathcal{C}|} \bigg) \leq \exp \bigg( \frac{-2(1/2 - \eta - \epsilon)^2 |F_n|^2}{K^2 |F_n|} \bigg) \\&\leq \exp\bigg( - \frac{1}{8K^2} \cdot |F_n| \bigg). \end{align*} $$
$$ \begin{align*} m \bigg\{ t' : \sum_{C \in \mathcal{C}} Y_C(t') < \epsilon|F_n| \bigg\} &\leq \exp\bigg( \frac{-2t^2}{K^2 |\mathcal{C}|} \bigg) \leq \exp \bigg( \frac{-2(1/2 - \eta - \epsilon)^2 |F_n|^2}{K^2 |F_n|} \bigg) \\&\leq \exp\bigg( - \frac{1}{8K^2} \cdot |F_n| \bigg). \end{align*} $$
The final inequality holds because
![]() $\epsilon = 1/100$
and
$\epsilon = 1/100$
and
![]() $\eta \ll \epsilon $
is small enough so that
$\eta \ll \epsilon $
is small enough so that
![]() $1/2 - \eta - \epsilon> 1/4$
.
$1/2 - \eta - \epsilon> 1/4$
.
Corollary 4.10. Let
![]() $y \in X_0$
. If B is any
$y \in X_0$
. If B is any
![]() $(\overline {Q}, T_{\alpha }, F_n)$
-Hamming ball of radius
$(\overline {Q}, T_{\alpha }, F_n)$
-Hamming ball of radius
![]() $\epsilon $
, then
$\epsilon $
, then
![]() $m_y(B) \leq \exp (( -{1}/{8K^2}) \cdot |F_n| )$
.
$m_y(B) \leq \exp (( -{1}/{8K^2}) \cdot |F_n| )$
.
Proof. If B does not meet the fiber above y, then obviously
![]() $m_y(B) = 0$
. Thus, assume
$m_y(B) = 0$
. Thus, assume
![]() $(y,s) \in B$
for some
$(y,s) \in B$
for some
![]() $s \in I$
. Then applying the triangle inequality in the space
$s \in I$
. Then applying the triangle inequality in the space
![]() $(\{0,1\}^{F_n}, d_{F_n})$
shows that
$(\{0,1\}^{F_n}, d_{F_n})$
shows that
![]() $B \subseteq B_{\operatorname {Ham}}(\overline {Q}, T_{\alpha }, F_n, (y,s), 2\epsilon )$
. Now apply Proposition 4.9 with
$B \subseteq B_{\operatorname {Ham}}(\overline {Q}, T_{\alpha }, F_n, (y,s), 2\epsilon )$
. Now apply Proposition 4.9 with
![]() $2\epsilon $
in place of
$2\epsilon $
in place of
![]() $\epsilon $
. The proof goes through exactly the same and we get the same constant
$\epsilon $
. The proof goes through exactly the same and we get the same constant
![]() $1/8K^2$
in the final estimate because
$1/8K^2$
in the final estimate because
![]() $\epsilon $
and
$\epsilon $
and
![]() $\eta $
are small enough so that
$\eta $
are small enough so that
![]() $1/2-\eta - 2\epsilon $
is still greater than
$1/2-\eta - 2\epsilon $
is still greater than
![]() $ 1/4$
.
$ 1/4$
.
Corollary 4.11. We have
![]() $\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m) \geq \tfrac 12 \exp (({1}/{8K^2}) \cdot |F_n|)$
.
$\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m) \geq \tfrac 12 \exp (({1}/{8K^2}) \cdot |F_n|)$
.
Proof. Let
![]() $\{ B_i \}_{i=1}^{\ell }$
be a collection of
$\{ B_i \}_{i=1}^{\ell }$
be a collection of
![]() $(\overline {Q}, T_{\alpha }, F_n)$
-Hamming balls of radius
$(\overline {Q}, T_{\alpha }, F_n)$
-Hamming balls of radius
![]() $\epsilon $
such that
$\epsilon $
such that
 $$ \begin{align*} (\mu \times m) \bigg( \bigcup B_i \bigg)> 1-\epsilon. \end{align*} $$
$$ \begin{align*} (\mu \times m) \bigg( \bigcup B_i \bigg)> 1-\epsilon. \end{align*} $$
Then
 $$ \begin{align*} &1-\epsilon < (\mu \times m) \bigg( \bigcup B_i \bigg) \\&\quad= (\mu \times m) \bigg( \bigcup B_i \cap (X_0 \times I) \bigg) + (\mu \times m) \bigg( \bigcup B_i \cap (X_0^c \times I) \bigg) \\&\quad< \sum_{i=1}^{\ell} (\mu \times m)(B_i \cap (X_0 \times I)) + (\mu \times m)(X_0^c \times I) \\&\quad< \sum_{i=1}^{\ell} \int_{y\in X_0} m_y(B_i) \,d\mu(y) + 2\eta \\&\quad< \ell \cdot \exp\bigg( -\frac{1}{8K^2} \cdot |F_n| \bigg) + 2\eta, \end{align*} $$
$$ \begin{align*} &1-\epsilon < (\mu \times m) \bigg( \bigcup B_i \bigg) \\&\quad= (\mu \times m) \bigg( \bigcup B_i \cap (X_0 \times I) \bigg) + (\mu \times m) \bigg( \bigcup B_i \cap (X_0^c \times I) \bigg) \\&\quad< \sum_{i=1}^{\ell} (\mu \times m)(B_i \cap (X_0 \times I)) + (\mu \times m)(X_0^c \times I) \\&\quad< \sum_{i=1}^{\ell} \int_{y\in X_0} m_y(B_i) \,d\mu(y) + 2\eta \\&\quad< \ell \cdot \exp\bigg( -\frac{1}{8K^2} \cdot |F_n| \bigg) + 2\eta, \end{align*} $$
implying that
![]() $\ell> (1-\epsilon -2\eta ) \exp (( {1}/{8K^2}) \cdot |F_n| ) > (1/2) \exp (( {1}/{8K^2}) \cdot |F_n| )$
.
$\ell> (1-\epsilon -2\eta ) \exp (( {1}/{8K^2}) \cdot |F_n| ) > (1/2) \exp (( {1}/{8K^2}) \cdot |F_n| )$
.
Our choice of n at the beginning now guarantees that
![]() $\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m) \geq \tfrac 12 \exp ({1}/{8K^2} \cdot |F_n|)> a_n$
, showing that
$\operatorname {\mathrm {cov}}(\overline {Q}, T_{\alpha }, F_n, \mu \times m) \geq \tfrac 12 \exp ({1}/{8K^2} \cdot |F_n|)> a_n$
, showing that
![]() $\alpha \in \mathcal {U}_N$
as desired. This completes the proof of Proposition 3.4.
$\alpha \in \mathcal {U}_N$
as desired. This completes the proof of Proposition 3.4.
Acknowledgements
I am grateful to Tim Austin for originally suggesting this project and for endless guidance. I also thank Benjy Weiss and an anonymous referee for pointing out some referencing inaccuracies in earlier versions. This project was partially supported by NSF grant DMS-1855694.
A Appendix. Measurability of the perturbed cocycle
In this section, we give a more careful proof of Proposition 4.7 that addresses the issue of measurability. We need to use at some point the following measurable selector theorem [Reference FremlinFre06, Proposition 433F].
Theorem A.1. Let
![]() $(\Omega _1, \mathcal {F}_1)$
and
$(\Omega _1, \mathcal {F}_1)$
and
![]() $(\Omega _2, \mathcal {F}_2)$
be standard Borel spaces. Let
$(\Omega _2, \mathcal {F}_2)$
be standard Borel spaces. Let
![]() $\mathbb {P}$
be a probability measure on
$\mathbb {P}$
be a probability measure on
![]() $(\Omega _1, \mathcal {F}_1)$
and suppose that
$(\Omega _1, \mathcal {F}_1)$
and suppose that
![]() $f: \Omega _2 \to \Omega _1$
is measurable and surjective. Then there exists a measurable selector
$f: \Omega _2 \to \Omega _1$
is measurable and surjective. Then there exists a measurable selector
![]() $g: \Omega _1 \to \Omega _2$
which is defined
$g: \Omega _1 \to \Omega _2$
which is defined
![]() $\mathbb {P}$
-almost everywhere (meaning
$\mathbb {P}$
-almost everywhere (meaning
![]() $g(\omega ) \in f^{-1}(\omega )$
for
$g(\omega ) \in f^{-1}(\omega )$
for
![]() $\mathbb {P}$
-almost every
$\mathbb {P}$
-almost every
![]() $\omega \in \Omega _1$
).
$\omega \in \Omega _1$
).
Given
![]() $x \in X$
, there is a natural bijection between
$x \in X$
, there is a natural bijection between
![]() $T^G x$
and G because T is a free action. We can also identify subsets: if
$T^G x$
and G because T is a free action. We can also identify subsets: if
![]() $E \subseteq T^G x$
, then we write
$E \subseteq T^G x$
, then we write
![]() $\widetilde {E} := \{g \in G : T^g x \in E \}$
. Note that this set depends on the ‘base point’ x. If x and y are two points in the same G-orbit, then the set
$\widetilde {E} := \{g \in G : T^g x \in E \}$
. Note that this set depends on the ‘base point’ x. If x and y are two points in the same G-orbit, then the set
![]() $\widetilde {E}$
based at x is a translate of the same set based at y. It will always be clear from context what the intended base point is.
$\widetilde {E}$
based at x is a translate of the same set based at y. It will always be clear from context what the intended base point is.
Definition A.2. A pattern in G is a pair
![]() $(H,\mathscr {C})$
, where H is a finite subset of G and
$(H,\mathscr {C})$
, where H is a finite subset of G and
![]() $\mathscr {C}$
is a partition of H.
$\mathscr {C}$
is a partition of H.
Definition A.3. For
![]() $x \in X$
, define
$x \in X$
, define
![]() $\operatorname {\mathrm {pat}}_n(x)$
to be the pattern
$\operatorname {\mathrm {pat}}_n(x)$
to be the pattern
![]() $(H,\mathscr {C})$
, where
$(H,\mathscr {C})$
, where
![]() $H = \widetilde {R_n(x)}$
and
$H = \widetilde {R_n(x)}$
and
![]() $\mathscr {C}$
is the partition of H into the sets
$\mathscr {C}$
is the partition of H into the sets
![]() $\widetilde {C}$
where C ranges over all of the
$\widetilde {C}$
where C ranges over all of the
![]() $R_{n-1}$
-cells contained in
$R_{n-1}$
-cells contained in
![]() $R_n(x)$
.
$R_n(x)$
.
Lemma A.4. The pattern
![]() $\operatorname {\mathrm {pat}}_n(x)$
is a measurable function of x.
$\operatorname {\mathrm {pat}}_n(x)$
is a measurable function of x.
Proof. Because there are only countably many possible patterns, it is enough to fix a pattern
![]() $(H, \mathscr {C})$
and show that
$(H, \mathscr {C})$
and show that
![]() $\{x : \operatorname {\mathrm {pat}}_n(x) = (H, \mathscr {C}) \}$
is measurable. Enumerate
$\{x : \operatorname {\mathrm {pat}}_n(x) = (H, \mathscr {C}) \}$
is measurable. Enumerate
![]() ${\mathscr {C} = \{C_1, \ldots , C_k \}}$
. Saying that
${\mathscr {C} = \{C_1, \ldots , C_k \}}$
. Saying that
![]() $\operatorname {\mathrm {pat}}_n(x) = (H,\mathscr {C})$
is the same as saying that
$\operatorname {\mathrm {pat}}_n(x) = (H,\mathscr {C})$
is the same as saying that
![]() $T^H x = R_n(x)$
and each
$T^H x = R_n(x)$
and each
![]() $T^{C_i}x$
is a cell of
$T^{C_i}x$
is a cell of
![]() $R_{n-1}$
. We can express the set of x satisfying this as
$R_{n-1}$
. We can express the set of x satisfying this as
 $$ \begin{align*} &\bigg( \bigcap_{i=1}^{k} \bigcap_{g,h \in C_i} \!\{x : (T^g x, T^h x) \in R_{n-1} \} \quad \cap \quad \bigcap_{(g, h) \in G^2 \setminus \bigcup (C_i \times C_i)} \!\{x : (T^g x, T^h x) \not\in R_{n-1} \} \bigg) \\&\quad\cap\,\bigg( \bigcap_{g \in H} \{x : (x, T^g x) \in R_n \} \quad \cap \quad \bigcap_{g \not\in H} \{x : (x,T^g x) \not\in R_n \} \bigg). \end{align*} $$
$$ \begin{align*} &\bigg( \bigcap_{i=1}^{k} \bigcap_{g,h \in C_i} \!\{x : (T^g x, T^h x) \in R_{n-1} \} \quad \cap \quad \bigcap_{(g, h) \in G^2 \setminus \bigcup (C_i \times C_i)} \!\{x : (T^g x, T^h x) \not\in R_{n-1} \} \bigg) \\&\quad\cap\,\bigg( \bigcap_{g \in H} \{x : (x, T^g x) \in R_n \} \quad \cap \quad \bigcap_{g \not\in H} \{x : (x,T^g x) \not\in R_n \} \bigg). \end{align*} $$
Because each
![]() $R_n$
is a measurable set and each
$R_n$
is a measurable set and each
![]() $T^g$
is a measurable map, this whole thing is measurable.
$T^g$
is a measurable map, this whole thing is measurable.
For each pattern
![]() $(H,\mathscr {C})$
, let
$(H,\mathscr {C})$
, let
![]() $X_{H,\mathscr {C}}^{(n)} = \{x \in X : \operatorname {\mathrm {pat}}_n(x) = (H, \mathscr {C}) \}$
. We define our cocycle
$X_{H,\mathscr {C}}^{(n)} = \{x \in X : \operatorname {\mathrm {pat}}_n(x) = (H, \mathscr {C}) \}$
. We define our cocycle
![]() $\alpha $
inductively on the equivalence relations
$\alpha $
inductively on the equivalence relations
![]() $R_n$
. For each n, the sets
$R_n$
. For each n, the sets
![]() $X_{H,\mathscr {C}}^{(n)}$
partition X into countably many measurable sets, so it will be enough to define
$X_{H,\mathscr {C}}^{(n)}$
partition X into countably many measurable sets, so it will be enough to define
![]() $\alpha $
measurably on each
$\alpha $
measurably on each
![]() $X_{H,\mathscr {C}}^{(n)}$
. At this point, fix a pattern
$X_{H,\mathscr {C}}^{(n)}$
. At this point, fix a pattern
![]() $(H,\mathscr {C})$
, fix
$(H,\mathscr {C})$
, fix
![]() $n = 2$
, and write
$n = 2$
, and write
![]() $X_{H, \mathscr {C}}$
instead of
$X_{H, \mathscr {C}}$
instead of
![]() $X_{H,\mathscr {C}}^{(2)}$
. Define
$X_{H,\mathscr {C}}^{(2)}$
. Define
 $$ \begin{align*} \Omega_2^{H,\mathscr{C}} &= \{ \psi : H \times H \to \operatorname{\mathrm{Aut}}(I,m) : \psi(h_1, h_3)\\ &= \psi(h_2, h_3) \circ \psi(h_1, h_2) \text{ for all } h_1,h_2,h_3 \in H \}, \\ \Omega_1^{H,\mathscr{C}} &= \bigg\{ \sigma : \bigcup_{C \in \mathscr{C}} C \times C \to \operatorname{\mathrm{Aut}}(I,m) : \sigma(g_1, g_3)\\ & = \sigma(g_2, g_3) \circ \sigma(g_1, g_2) \text{ for all } g_1,g_2,g_3 \in G \bigg\}, \\ \Omega_2^{H,\mathscr{C},\text{ ind}} &= \{ \psi \in \Omega_2^{H,\mathscr{C}} : \psi \ \text{is } (H,\mathscr{C})\text{-independent} \}, \end{align*} $$
$$ \begin{align*} \Omega_2^{H,\mathscr{C}} &= \{ \psi : H \times H \to \operatorname{\mathrm{Aut}}(I,m) : \psi(h_1, h_3)\\ &= \psi(h_2, h_3) \circ \psi(h_1, h_2) \text{ for all } h_1,h_2,h_3 \in H \}, \\ \Omega_1^{H,\mathscr{C}} &= \bigg\{ \sigma : \bigcup_{C \in \mathscr{C}} C \times C \to \operatorname{\mathrm{Aut}}(I,m) : \sigma(g_1, g_3)\\ & = \sigma(g_2, g_3) \circ \sigma(g_1, g_2) \text{ for all } g_1,g_2,g_3 \in G \bigg\}, \\ \Omega_2^{H,\mathscr{C},\text{ ind}} &= \{ \psi \in \Omega_2^{H,\mathscr{C}} : \psi \ \text{is } (H,\mathscr{C})\text{-independent} \}, \end{align*} $$
where
![]() $\psi \in \Omega _2^{H,\mathscr {C}}$
is said to be
$\psi \in \Omega _2^{H,\mathscr {C}}$
is said to be
![]() $(H,\mathscr {C})$
-independent if for any fixed
$(H,\mathscr {C})$
-independent if for any fixed
![]() $h_0 \in H$
, the partitions
$h_0 \in H$
, the partitions
as C ranges over
![]() $\mathscr {C}$
are independent with respect to m.
$\mathscr {C}$
are independent with respect to m.
Proposition A.5. For every
![]() $\sigma \in \Omega _1^{H,\mathscr {C}}$
, there is some
$\sigma \in \Omega _1^{H,\mathscr {C}}$
, there is some
![]() $\psi \in \Omega _2^{H,\mathscr {C},\text {ind}}$
that extends
$\psi \in \Omega _2^{H,\mathscr {C},\text {ind}}$
that extends
![]() $\sigma $
.
$\sigma $
.
Proof. The idea is exactly the same as the construction described in steps 3–5 in the sketched proof of Proposition 4.7, but we write it out here also for completeness.
Enumerate
![]() $\mathscr {C} = \{C_1, \ldots , C_k \}$
and for each i fix an element
$\mathscr {C} = \{C_1, \ldots , C_k \}$
and for each i fix an element
![]() $g_i \in C_i$
. First, obviously we define
$g_i \in C_i$
. First, obviously we define
![]() $\psi = \sigma $
on each
$\psi = \sigma $
on each
![]() $C_i \times C_i$
. Next, define
$C_i \times C_i$
. Next, define
![]() $\psi (g_1, g_2)$
to be an element of
$\psi (g_1, g_2)$
to be an element of
![]() $\operatorname {\mathrm {Aut}}(I,m)$
such that
$\operatorname {\mathrm {Aut}}(I,m)$
such that
 $$ \begin{align*} \bigvee_{g \in C_1} \sigma(g_1, g)^{-1} \pi \quad \text{and} \quad \psi(g_1, g_2)^{-1} \bigg(\bigvee_{g \in C_2} \sigma(g_2, g)^{-1} \pi \bigg) \end{align*} $$
$$ \begin{align*} \bigvee_{g \in C_1} \sigma(g_1, g)^{-1} \pi \quad \text{and} \quad \psi(g_1, g_2)^{-1} \bigg(\bigvee_{g \in C_2} \sigma(g_2, g)^{-1} \pi \bigg) \end{align*} $$
are independent. Then, define
![]() $\psi $
on all of
$\psi $
on all of
![]() $(C_1 \cup C_2) \times (C_1 \cup C_2)$
by setting
$(C_1 \cup C_2) \times (C_1 \cup C_2)$
by setting
 $$ \begin{align*} \psi(h_1, h_2) &= \sigma(g_2, h_2) \circ \psi(g_1, g_2) \circ \sigma(h_1, g_1) \quad \text{and} \\ \psi(h_2, h_1) &= \psi(h_1, h_2)^{-1} \end{align*} $$
$$ \begin{align*} \psi(h_1, h_2) &= \sigma(g_2, h_2) \circ \psi(g_1, g_2) \circ \sigma(h_1, g_1) \quad \text{and} \\ \psi(h_2, h_1) &= \psi(h_1, h_2)^{-1} \end{align*} $$
for any
![]() $h_1 \in C_1, h_2 \in C_2$
. Continue this definition inductively, making each new step independent of all the steps that came before it. If
$h_1 \in C_1, h_2 \in C_2$
. Continue this definition inductively, making each new step independent of all the steps that came before it. If
![]() $\psi $
has been defined on
$\psi $
has been defined on
![]() $( C_1 \cup \dots \cup C_j ) \times ( C_1 \cup \dots \cup C_j )$
, then define
$( C_1 \cup \dots \cup C_j ) \times ( C_1 \cup \dots \cup C_j )$
, then define
![]() $\psi (g_1, g_{j+1})$
to be an element of
$\psi (g_1, g_{j+1})$
to be an element of
![]() $\operatorname {\mathrm {Aut}}(I,m)$
such that
$\operatorname {\mathrm {Aut}}(I,m)$
such that
 $$ \begin{align*} \bigvee_{g \in C_1 \cup \dots \cup C_j} \psi(g_1, g)^{-1}\pi \quad \text{and} \quad \psi(g_1,g_{j+1})^{-1} \bigg( \bigvee_{g' \in C_{j+1}} \sigma(g_{j+1}, g')^{-1}\pi \bigg) \end{align*} $$
$$ \begin{align*} \bigvee_{g \in C_1 \cup \dots \cup C_j} \psi(g_1, g)^{-1}\pi \quad \text{and} \quad \psi(g_1,g_{j+1})^{-1} \bigg( \bigvee_{g' \in C_{j+1}} \sigma(g_{j+1}, g')^{-1}\pi \bigg) \end{align*} $$
are independent. Then extend the definition of
![]() $\psi $
to all of
$\psi $
to all of
![]() $(C_1 \cup \dots \cup C_{j+1}) \times (C_1 \cup \dots \cup C_{j+1})$
in the exact same way.
$(C_1 \cup \dots \cup C_{j+1}) \times (C_1 \cup \dots \cup C_{j+1})$
in the exact same way.
At the end of this process,
![]() $\psi $
has been defined on
$\psi $
has been defined on
![]() $(C_1 \cup \cdots \cup C_k) \times (C_1 \cup \cdots \cup C_k) = H \times H$
, and it satisfies the cocycle condition by construction. To verify that it also satisfies the independence condition, note that the construction has guaranteed that
$(C_1 \cup \cdots \cup C_k) \times (C_1 \cup \cdots \cup C_k) = H \times H$
, and it satisfies the cocycle condition by construction. To verify that it also satisfies the independence condition, note that the construction has guaranteed that
are independent partitions as C ranges over
![]() $\mathscr {C}$
. To get the same conclusion for an arbitrary base point
$\mathscr {C}$
. To get the same conclusion for an arbitrary base point
![]() $h_0$
, pull everything back by the fixed map
$h_0$
, pull everything back by the fixed map
![]() $\psi (h_0, g_1)$
. Because this map is measure preserving, pulling back all of the partitions by it preserves their independence.
$\psi (h_0, g_1)$
. Because this map is measure preserving, pulling back all of the partitions by it preserves their independence.
Now we would like to take this information about cocycles defined on patterns and use it to produce cocycles defined on the actual space X. Define the map
![]() $\sigma ^{H,\mathscr {C}}: X_{H,\mathscr {C}} \to \Omega _1^{H,\mathscr {C}}$
by
$\sigma ^{H,\mathscr {C}}: X_{H,\mathscr {C}} \to \Omega _1^{H,\mathscr {C}}$
by
![]() $\sigma ^{H,\mathscr {C}}_x(g_1, g_2) := \alpha _0(T^{g_1}x, T^{g_2} x)$
. Note that this is a measurable map because
$\sigma ^{H,\mathscr {C}}_x(g_1, g_2) := \alpha _0(T^{g_1}x, T^{g_2} x)$
. Note that this is a measurable map because
![]() $\alpha _0$
is a measurable cocycle.
$\alpha _0$
is a measurable cocycle.
By Theorem A.1 applied to the measure
![]() $\mathbb {P} = (\sigma ^{H, \mathscr {C}})_* (\mu (\cdot \,|\, X_{H,\mathscr {C}})) \in \operatorname {\mathrm {Prob}}(\Omega _1^{H,\mathscr {C}})$
, we get a measurable map
$\mathbb {P} = (\sigma ^{H, \mathscr {C}})_* (\mu (\cdot \,|\, X_{H,\mathscr {C}})) \in \operatorname {\mathrm {Prob}}(\Omega _1^{H,\mathscr {C}})$
, we get a measurable map
![]() $E^{H,\mathscr {C}}: \Omega _1^{H,\mathscr {C}} \to \Omega _2^{H,\mathscr {C},\text {ind}}$
defined
$E^{H,\mathscr {C}}: \Omega _1^{H,\mathscr {C}} \to \Omega _2^{H,\mathscr {C},\text {ind}}$
defined
![]() $\mathbb {P}$
-almost everywhere such that
$\mathbb {P}$
-almost everywhere such that
![]() $E^{H,\mathscr {C}}(\sigma )$
extends
$E^{H,\mathscr {C}}(\sigma )$
extends
![]() $\sigma $
. Denote the composition
$\sigma $
. Denote the composition
![]() $E^{H,\mathscr {C}} \circ \sigma ^{H,\mathscr {C}}$
by
$E^{H,\mathscr {C}} \circ \sigma ^{H,\mathscr {C}}$
by
![]() $\psi ^{H, \mathscr {C}}$
and write the image of x under this map as
$\psi ^{H, \mathscr {C}}$
and write the image of x under this map as
![]() $\psi ^{H, \mathscr {C}}_x$
. To summarize, for every pattern
$\psi ^{H, \mathscr {C}}_x$
. To summarize, for every pattern
![]() $(H,\mathscr {C})$
, there is a measurable map
$(H,\mathscr {C})$
, there is a measurable map
![]() $\psi ^{H,\mathscr {C}} : X_{H,\mathscr {C}} \to \Omega _2^{H,\mathscr {C},\text {ind}}$
defined
$\psi ^{H,\mathscr {C}} : X_{H,\mathscr {C}} \to \Omega _2^{H,\mathscr {C},\text {ind}}$
defined
![]() $\mu $
-almost everywhere with the property that
$\mu $
-almost everywhere with the property that
![]() $\psi ^{H, \mathscr {C}}_x$
extends
$\psi ^{H, \mathscr {C}}_x$
extends
![]() $\sigma ^{H,\mathscr {C}}_x$
.
$\sigma ^{H,\mathscr {C}}_x$
.
It is now natural to define our desired cocycle
![]() $\alpha $
on the equivalence relation
$\alpha $
on the equivalence relation
![]() $R_2$
by the formula
$R_2$
by the formula
![]() $\alpha (x, T^g x) := \psi ^{\operatorname {\mathrm {pat}}_2(x)}_x(e, g)$
. It is then immediate to verify the two properties of
$\alpha (x, T^g x) := \psi ^{\operatorname {\mathrm {pat}}_2(x)}_x(e, g)$
. It is then immediate to verify the two properties of
![]() $\alpha $
claimed in the statement of Proposition 4.7. The fact that
$\alpha $
claimed in the statement of Proposition 4.7. The fact that
![]() $\alpha $
agrees with
$\alpha $
agrees with
![]() $\alpha _0$
on
$\alpha _0$
on
![]() $R_1$
follows from the fact that
$R_1$
follows from the fact that
![]() $\psi _{H,\mathscr {C}}$
extends
$\psi _{H,\mathscr {C}}$
extends
![]() $\sigma ^{H,\mathscr {C}}$
and the claimed independence property of
$\sigma ^{H,\mathscr {C}}$
and the claimed independence property of
![]() $\alpha $
translates directly from the independence property that the
$\alpha $
translates directly from the independence property that the
![]() $\psi ^{H,\mathscr {C}}_x$
were constructed to have (see also the discussion after step 6 in the sketched proof of Proposition 4.7). In addition,
$\psi ^{H,\mathscr {C}}_x$
were constructed to have (see also the discussion after step 6 in the sketched proof of Proposition 4.7). In addition,
![]() $\alpha $
is measurable because for each fixed g, the map
$\alpha $
is measurable because for each fixed g, the map
![]() $x \mapsto \alpha (x, T^g x)$
is simply a composition of other maps already determined to be measurable. The only problem is that
$x \mapsto \alpha (x, T^g x)$
is simply a composition of other maps already determined to be measurable. The only problem is that
![]() $\alpha $
, when defined in this way, need not satisfy the cocycle condition. To see why, observe that the cocycle condition
$\alpha $
, when defined in this way, need not satisfy the cocycle condition. To see why, observe that the cocycle condition
![]() $\alpha (x, T^h x) = \alpha (T^g x, T^h x) \circ \alpha (x, T^g x)$
is equivalent to the condition
$\alpha (x, T^h x) = \alpha (T^g x, T^h x) \circ \alpha (x, T^g x)$
is equivalent to the condition
However, in defining the maps
![]() $\psi ^{H,\mathscr {C}}$
, we have simply applied Theorem A.1 arbitrarily to each pattern separately, so
$\psi ^{H,\mathscr {C}}$
, we have simply applied Theorem A.1 arbitrarily to each pattern separately, so
![]() $\psi ^{\operatorname {\mathrm {pat}}_2(x)}$
and
$\psi ^{\operatorname {\mathrm {pat}}_2(x)}$
and
![]() $\psi ^{\operatorname {\mathrm {pat}}_2(T^g x)}$
have nothing to do with each other. However, we can fix this problem with a little extra work, and once we do, we will have defined
$\psi ^{\operatorname {\mathrm {pat}}_2(T^g x)}$
have nothing to do with each other. However, we can fix this problem with a little extra work, and once we do, we will have defined
![]() $\alpha : R_2 \to \operatorname {\mathrm {Aut}}(I,m)$
with all of the desired properties.
$\alpha : R_2 \to \operatorname {\mathrm {Aut}}(I,m)$
with all of the desired properties.
Start by declaring two patterns as equivalent if they are translates of each other, and fix a choice of one pattern from each equivalence class. As there are only countably many patterns in total, there is no need to worry about how to make this choice. For each representative pattern
![]() $(H_0, \mathscr {C}_0)$
, apply Theorem A.1 arbitrarily to get a map
$(H_0, \mathscr {C}_0)$
, apply Theorem A.1 arbitrarily to get a map
![]() $\psi ^{H_0, \mathscr {C}_0}$
. This does not cause any problems because two patterns that are not translates of each other cannot appear in the same orbit (this follows from the easy fact that
$\psi ^{H_0, \mathscr {C}_0}$
. This does not cause any problems because two patterns that are not translates of each other cannot appear in the same orbit (this follows from the easy fact that
![]() $\operatorname {\mathrm {pat}}_2(T^g x) = g^{-1} \cdot \operatorname {\mathrm {pat}}_2(x)$
), so it does not matter that their
$\operatorname {\mathrm {pat}}_2(T^g x) = g^{-1} \cdot \operatorname {\mathrm {pat}}_2(x)$
), so it does not matter that their
![]() $\psi $
maps are not coordinated with each other. For convenience, let us denote the representative of the equivalence class of
$\psi $
maps are not coordinated with each other. For convenience, let us denote the representative of the equivalence class of
![]() $\operatorname {\mathrm {pat}}_2(x)$
by
$\operatorname {\mathrm {pat}}_2(x)$
by
![]() $\operatorname {\mathrm {rp}}(x)$
. Now, for every
$\operatorname {\mathrm {rp}}(x)$
. Now, for every
![]() $x \in X$
, let
$x \in X$
, let
![]() $g^*(x)$
be the unique element of G with the property that
$g^*(x)$
be the unique element of G with the property that
![]() $\operatorname {\mathrm {pat}}_2(T^{g^*(x)} x) = \operatorname {\mathrm {rp}}(x)$
. Note that the maps
$\operatorname {\mathrm {pat}}_2(T^{g^*(x)} x) = \operatorname {\mathrm {rp}}(x)$
. Note that the maps
![]() $g^*$
and
$g^*$
and
![]() $\operatorname {\mathrm {rp}}$
are both constant on each subset
$\operatorname {\mathrm {rp}}$
are both constant on each subset
![]() $X_{H,\mathscr {C}}$
and are therefore measurable.
$X_{H,\mathscr {C}}$
and are therefore measurable.
Now for an arbitrary pattern
![]() $(H,\mathscr {C})$
and
$(H,\mathscr {C})$
and
![]() $x \in X_{H,\mathscr {C}}$
, we define the map
$x \in X_{H,\mathscr {C}}$
, we define the map
![]() $\psi ^{H,\mathscr {C}}$
by
$\psi ^{H,\mathscr {C}}$
by
Note that this is still just a composition of measurable functions, so
![]() $\psi ^{H,\mathscr {C}}$
is measurable. All that remains is to verify that this definition satisfies (A.1). The right-hand side of (A.1) is
$\psi ^{H,\mathscr {C}}$
is measurable. All that remains is to verify that this definition satisfies (A.1). The right-hand side of (A.1) is
 $$ \begin{align*} &\psi_{T^{g^*(T^g x)} T^g x}^{\operatorname{\mathrm{rp}}(T^gx)} ( e g^*(T^g x)^{-1}, hg^{-1} g^*(T^g x)^{-1} ) \circ \psi_{T^{g^*(x)} x}^{\operatorname{\mathrm{rp}}(x)} ( e g^*(x)^{-1}, g g^*(x)^{-1} ) \\&\quad= \psi_{T^{g^*(x)g^{-1}}T^g x}^{\operatorname{\mathrm{rp}}(x)} ( (g^*(x)g^{-1})^{-1}, hg^{-1} (g^*(x)g^{-1})^{-1} ) \circ \psi_{T^{g^*(x)} x}^{\operatorname{\mathrm{rp}}(x)} (g^*(x)^{-1}, g g^*(x)^{-1} ) \\&\quad= \psi_{T^{g^*(x)} x}^{\operatorname{\mathrm{rp}}(x)} ( g g^*(x)^{-1} , hg^*(x)^{-1} ) \circ \psi_{T^{g^*(x)} x}^{\operatorname{\mathrm{rp}}(x)} (g^*(x)^{-1}, g g^*(x)^{-1} ) \\&\quad= \psi_{T^{g^*(x)} x}^{\operatorname{\mathrm{rp}}(x)}( g^*(x)^{-1}, hg^*(x)^{-1} ), \end{align*} $$
$$ \begin{align*} &\psi_{T^{g^*(T^g x)} T^g x}^{\operatorname{\mathrm{rp}}(T^gx)} ( e g^*(T^g x)^{-1}, hg^{-1} g^*(T^g x)^{-1} ) \circ \psi_{T^{g^*(x)} x}^{\operatorname{\mathrm{rp}}(x)} ( e g^*(x)^{-1}, g g^*(x)^{-1} ) \\&\quad= \psi_{T^{g^*(x)g^{-1}}T^g x}^{\operatorname{\mathrm{rp}}(x)} ( (g^*(x)g^{-1})^{-1}, hg^{-1} (g^*(x)g^{-1})^{-1} ) \circ \psi_{T^{g^*(x)} x}^{\operatorname{\mathrm{rp}}(x)} (g^*(x)^{-1}, g g^*(x)^{-1} ) \\&\quad= \psi_{T^{g^*(x)} x}^{\operatorname{\mathrm{rp}}(x)} ( g g^*(x)^{-1} , hg^*(x)^{-1} ) \circ \psi_{T^{g^*(x)} x}^{\operatorname{\mathrm{rp}}(x)} (g^*(x)^{-1}, g g^*(x)^{-1} ) \\&\quad= \psi_{T^{g^*(x)} x}^{\operatorname{\mathrm{rp}}(x)}( g^*(x)^{-1}, hg^*(x)^{-1} ), \end{align*} $$
which is, by definition, equal to the left-hand side of (A.1) as desired.
This, together with the discussion surrounding (A.1), shows that if we construct the maps
![]() $\psi ^{H,\mathscr {C}}$
in this way, then making the definition
$\psi ^{H,\mathscr {C}}$
in this way, then making the definition
![]() $\alpha (x, T^g x) = \psi _x^{\operatorname {\mathrm {pat}}_2(x)}(e,g)$
gives us a true measurable cocycle with all of the desired properties. Finally, to extend the definition of
$\alpha (x, T^g x) = \psi _x^{\operatorname {\mathrm {pat}}_2(x)}(e,g)$
gives us a true measurable cocycle with all of the desired properties. Finally, to extend the definition of
![]() $\alpha $
to
$\alpha $
to
![]() $R_n$
with
$R_n$
with
![]() $n \geq 3$
, repeat the exact same process, except it is even easier because there is no need to force any independence. The maps
$n \geq 3$
, repeat the exact same process, except it is even easier because there is no need to force any independence. The maps
![]() $\psi ^{H,\mathscr {C}}$
only need to be measurable selections into the space
$\psi ^{H,\mathscr {C}}$
only need to be measurable selections into the space
![]() $\Omega _2^{H,\mathscr {C}}$
, and then everything else proceeds in exactly the same way.
$\Omega _2^{H,\mathscr {C}}$
, and then everything else proceeds in exactly the same way.