Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T04:21:27.529Z Has data issue: false hasContentIssue false
  • English
  • Français

Transitivity and invariant measures for the geometric model of the Lorenz equations

Published online by Cambridge University Press:  19 September 2008

Clark Robinson
Clark Robinson
Affiliation:
Department of Mathematics, Northwestern University, Evanston, IL 60201, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper concerns perturbations of the geometric model of the Lorenz equations and their associated one-dimensional Poincaré maps. R. Williams has shown that if a map of the interval of the type arising from the Lorenz equations satisfies f′(x) > 2½ everywhere except at the discontinuity then f is locally eventually onto (l.e.o.) and so topologically transitive [14]. We show roughly that if 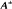are the end points of the interval, and their iterates 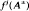stay on the same side of the point of discontinuity for 0 ≤ j ≤ k, and f′(x) > 21/(k+1) everywhere, then f is l.e.o. Secondly, we show that the one-dimensional Poincaré map of any Cr perturbation of the geometric model (for large enough r) has an ergodic measure which is equivalent to Lebesgue measure. This result follows by showing it is C1+α and satisfies a theorem of Keller, Wong, Lasota, Li & Yorke.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 4 , Issue 4 , December 1984 , pp. 605 - 611
Copyright
Copyright © Cambridge University Press 1984

References

REFERENCES

[1]Andronov, A. et al. Theory of Bifurcation of Dynamical Systems on the Plane. Wiley: New York, 1973.Google Scholar
[2]Belickii, G. R.. Functional equations and conjugacy of local difieomorphisms of finite smooth class. Sov. Math. Dokl. 13 (1972), 56–59.Google Scholar
[3]Bunimovich, L. A. & Sinai, Ya G.. Stochasticity of the attractor in the Lorenz model. In Nonlinear Waves, Proc. Winter School Gorki 1977, Nauka Moscow 1979, pp. 212–226.Google Scholar
[4]Guckenheimer, J. & Holmes, P.. Non-linear Oscillations, Dynamical Systems and Bifurcation of Vector Fields. Springer-Verlag: New York-Heidelberg-Berlin, 1983.CrossRefGoogle Scholar
[5]Guckenheimer, I. & Williams, R.. Structural stability of Lorenz attractors. Publ. IHES 50 (1979), 59–72.CrossRefGoogle Scholar
[6]Hirsch, M. & Pugh, C.. Stable manifolds and hyperbolic sets. In Proc. Symp. Pure Math. 14 (1970), Amer. Math. Soc. pp. 133–163.CrossRefGoogle Scholar
[7]Keller, G.. Generalized bounded variation and applications to piecewise monotonic transformations. Preprint, University of Heidelberg, 1981.Google Scholar
[8]Lasota, A. & Yorke, J., On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc. 186 (1973), 481–488.CrossRefGoogle Scholar
[9]Li, T. & Yorke, J.. Ergodic transformations from an interval into itself. Trans. Amer. Math. Soc. 235 (1978), 183–192.CrossRefGoogle Scholar
[10]Parry, W.. The Lorenz attractor and related population model. In Ergodic Theory Conference Oberwolfach (edited by Denker, M. and Jacobs, K.) Lecture Notes in Math. 729 (1979). Springer-Verlag: New York, pp. 169–187.CrossRefGoogle Scholar
[11]Robinson, C.. Differentiability of the stable foliations for the model Lorenz equations. In Dynamical Systems and Turbulence (edited by Rand, D. and Young, L. S.) Lecture Notes in Math. 898 (1981). Springer-Verlag: New York, pp. 302–315.Google Scholar
[12]Sinai, Ya G.. Hyperbolic conditions for Lorenz model. Phys. D 2 (1981), 3–7.CrossRefGoogle Scholar
[13]Sparrow, C.. The Lorenz Equations: Bifurcation, Chaos and Strange Attractors. Applied Math. Sci. 41. Springer-Verlag: New York-Heidelberg-Berlin, 1982.CrossRefGoogle Scholar
[14]Williams, R.. The structure of Lorenz attractors. Publ. IHES 50 (1979), 73–99.CrossRefGoogle Scholar
[15]Wong, S.. Some metric properties of piecewise monotonic mappings of the unit interval. Trans. Amer. Math. Soc. 246 (1978), 493–500.CrossRefGoogle Scholar
[16]Wong, S.. Hölder continuous derivatives and ergodic theory. London Math. Soc. 22 (1980), 506–520.CrossRefGoogle Scholar