Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T04:24:20.895Z Has data issue: false hasContentIssue false
  • English
  • Français

Subordinate Šil'nikov bifurcations near some singularities of vector fields having low codimension

Published online by Cambridge University Press:  19 September 2008

H. W. Broer  and
G. Vegter
H. W. Broer
Affiliation:
Mathematics Institute, Rijkuniversiteit Groningen, P.O. Box 800, 9700 A VGroningen, The Netherlands
G. Vegter
Affiliation:
Mathematics Institute, Rijkuniversiteit Groningen, P.O. Box 800, 9700 A VGroningen, The Netherlands
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

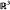A specific singularity of a vector field on is considered, of codimension 2 in the dissipative case and of codimension 1 in the conservative case. In both contexts in generic unfoldings the existence is proved of subordinate Šil'nikov bifurcations, which have codimension 1. Special attention is paid to the C∞-flatness of this subordinate phenomenon.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 4 , Issue 4 , December 1984 , pp. 509 - 525
Copyright
Copyright © Cambridge University Press 1984

References

REFERENCES

[0]Abraham, R. & Marsden, J. E.. Foundations of Mechanics. Benjamin, 1978.Google Scholar
[1]Arneodo, A., Coullet, P. & Tresser, C.. Possible new strange attractors with spiral structure. Commun. Math. Phys. 79 (1981), 573–579.CrossRefGoogle Scholar
[2]Broer, H. W.. Bifurcations of singularities in volume preserving vector fields. Ph.D. Thesis, Groningen 1979.Google Scholar
[3]Broer, H. W.. Formal normal forms for vector fields and some consequences for bifurcations in the volume preserving case. In Dynamical Systems and Turbulence, Warwick 1980. Springer Lecture Notes in Maths. 898.CrossRefGoogle Scholar
[4]Broer, H. W.. Quasi periodic flow near a codimension one singularity of a divergence free vector field in dimension three. In Dynamical Systems and Turbulence, Warwick 1980, Springer LNM 898.Google Scholar
[5]Broer, H. W. & van Strien, S. J.. Infinitely many moduli of strong stability in divergence free unfoldings of singularities of vector fields. Preprint IMPA, Rio de Janeiro 1981. In Geometric Dynamics, Proceedings, Rio de Janeiro 1981. Springer Lecture Notes in Maths. 1007.Google Scholar
[6]Carr, J.. Applications of Centre Manifold Theory. Springer Applied Math. Sciences 35, 1981.CrossRefGoogle Scholar
[7]Guckenheimer, J.. On a codimension two bifurcation. In Dynamical Systems and Turbulence, Warwick 1980, Springer LNM 898.Google Scholar
[8]Newhouse, S. E., Palis, J. & Takens, F.. Stable families of diffeomorphisms. Preprint IMPA, Rio de Janeiro 1979. To be published in Publ. Math. I.H.E.S.Google Scholar
[9]Palis, J. & de Melo, W. C.. lntroducão aos Sistemas Dinâmicos. E. Blücher: São Paulo, 1978.Google Scholar
[10]Poincaré, H.. Thèse. In Oevres 1, pp. LIX–CXXIX (1879). Gauthier-Villars 1928.Google Scholar
[11]Robinson, R. C.. Generic properties of conservative systems I, II. Amer. J. Math. 92 (1970), 562–603, 897–906.CrossRefGoogle Scholar
[12]Šil'nikov, L. P.. A case of the existence of a denumerable set of periodic motions. Soviet Math. Dokl. 6(1965), 163–166.Google Scholar
[13]Šil'nikov, L. P.. A contribution to the problem of the structure of an extended neighbourhood of a rough equilibrium state of saddle focus type. Math. USSR Sbornik 10 (1970), 91–102.CrossRefGoogle Scholar
[14]Sotomayor, J.. Generic bifurcations of dynamical systems. In Dynamical Systems. Academic Press, 1973.Google Scholar
[15]Takens, F.. A non-stabilisable jet of a singularity of a vector field. In Dynamical Systems. Academic Press, 1973.Google Scholar
[16]Takens, F.. Singularities of vector fields. Publ. Math. I.H.E.S. 43 (1974), 48–100.CrossRefGoogle Scholar
[17]Takens, F.. A non-stabilizable jet of a singularity of a vector field, the analytic case. Preprint IMPA, Rio de Janeiro 1982.Google Scholar