Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-29T11:33:10.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Stable intersections of conformal Cantor sets

Part of: Classical measure theory Local and nonlocal bifurcation theory Complex dynamical systems

Published online by Cambridge University Press:  25 October 2021

HUGO ARAÚJO  and
CARLOS GUSTAVO MOREIRA
HUGO ARAÚJO*
Affiliation:
Departamento de Ciências Exatas e Aplicadas, Universidade Federal de Ouro Preto, João Monlevade 35931-008, Minas Gerais, Brazil
CARLOS GUSTAVO MOREIRA
Affiliation:
Instituto de Matemática Pura e Aplicada, Rio de Janeiro 22460-320, Rio de Janeiro, Brazil (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate stable intersections of conformal Cantor sets and their consequences to dynamical systems. First we define this type of Cantor set and relate it to horseshoes appearing in automorphisms of 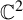$\mathbb {C}^2$ . Then we study limit geometries, that is, objects related to the asymptotic shape of the Cantor sets, to obtain a criterion that guarantees stable intersection between some configurations. Finally, we show that the Buzzard construction of a Newhouse region on 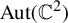$\mathrm{Aut}(\mathbb {C}^2)$ can be seen as a case of stable intersection of Cantor sets in our sense and give some (not optimal) estimate on how ‘thick’ those sets have to be.

Keywords

Cantor setssmooth dynamicsbifurcation theorysymbolic dynamics

MSC classification

Primary: 28A80: Fractals 37G25: Bifurcations connected with nontransversal intersection
Secondary: 37F99: None of the above, but in this section
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 1 , January 2023 , pp. 1 - 49
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Biebler, S.. A complex gap lemma. Proc. Amer. Math. Soc. 148(1) (2020), 351–364.Google Scholar
Bowen, R.. Markov partitions for Axiom A diffeomorphisms. Amer. J. Math. 92(3) (1970), 725–747.Google Scholar
Buzzard, G. T.. Persistent homoclinic tangencies and infinitely many sinks for automorphisms of ${\mathbb{C}}^2$ . PhD Thesis, University of Michigan, 1995.Google Scholar
Buzzard, G. T.. Infinitely many periodic attractors for holomorphic maps of 2 variables. Ann. of Math. (2) 145(2) (1997), 389–417.CrossRefGoogle Scholar
Constantine, G. M. and Savits, T. H.. A multivariate $\mathrm{Fa}$ á di Bruno formula with applications. Trans. Amer. Math. Soc. 348(2) (1996), 503–520.Google Scholar
Duarte, P.. Persistent homoclinic tangencies for conservative maps near the identity. Ergod. Th. & Dynam. Sys. 20(2) (2000), 393–438.Google Scholar
Dugundji, J.. Topology. Allyn and Bacon, Boston, 1966.Google Scholar
Dujardin, R. and Lyubich, M.. Stability and bifurcations for dissipative polynomial automorphisms of ${\mathbb{C}}^2$ . Invent. Math. 200(2) (2015), 439–511.Google Scholar
Hirsch, M. W., Palis, J., Pugh, C. C. and Shub, M.. Neighborhoods of hyperbolic sets. Invent. Math. 9 (1970), 121–134.Google Scholar
Moreira, C. G. and Yoccoz, J.-C.. Stable intersections of regular cantor sets with large Hausdorff dimensions. Ann. of Math. (2) 154(1) (2001), 45–96.CrossRefGoogle Scholar
Newhouse, S. E.. Nondensity of Axiom A(a) on ${S}^2$ . Global Analysis (Proceedings of Symposia in Pure Mathematics, XIV, Berkeley, CA, 1968). American Mathematical Society, Providence, RI, 1970, pp. 191–202.CrossRefGoogle Scholar
Newhouse, S. E.. Diffeomorphisms with infinitely many sinks. Topology 13 (1974), 9–18.Google Scholar
Newhouse, S. E.. The abundance of wild hyperbolic sets and nonsmooth stable sets for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 101–151.CrossRefGoogle Scholar
Oberste-Vorth, R. W.. Complex horseshoes and the dynamics of mappings of two complex variables. PhD Thesis, Cornell University, 1987.Google Scholar
Palis, J. and Takens, F.. Hyperbolicity and the creation of homoclinic orbits. Ann. of Math. (2) 125(2) (1987), 337–374.CrossRefGoogle Scholar
Palis, J. and Viana, M.. High dimension diffeomorphisms displaying infinitely many periodic attractors. Ann. of Math. (2) 140(1) (1994), 207–250.CrossRefGoogle Scholar
Pixton, D.. Markov neighborhoods for zero-dimensional basic sets. Trans. Amer. Math. Soc. 279(2) (1983), 431–462.CrossRefGoogle Scholar
Robinson, C.. Structural stability of $\mathcal{C}^1$ diffeomorphisms. J. Differential Equations 22(1) (1976), 28–73.Google Scholar
Shub, M.. Global Stability of Dynamical Systems. Springer-Verlag, New York, 1987.Google Scholar
Zamudio, A. M.. Complex cantor sets: scale recurrence lemma and dimension formula. PhD Thesis, IMPA, Rio de Janeiro, 2017.Google Scholar