Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T04:18:18.582Z Has data issue: false hasContentIssue false
  • English
  • Français

Smale solenoid attractors and affine Hirsch foliations

Published online by Cambridge University Press:  04 May 2017

BIN YU
BIN YU*
Affiliation:
School of Mathematical Sciences, Tongji University, Shanghai 200092, China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The main purpose of this paper is to study north–south Smale solenoid diffeomorphisms on $3$-manifolds by using affine Hirsch foliations. A north–south Smale solenoid diffeomorphism 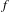$f$ on a closed $3$-manifold 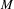$M$ is a diffeomorphism whose non-wandering set is composed of a Smale solenoid attractor 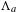$\unicode[STIX]{x1D6EC}_{a}$ and a Smale solenoid repeller 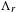$\unicode[STIX]{x1D6EC}_{r}$. The key observation is that a north–south Smale solenoid diffeomorphism 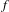$f$ automatically induces two non-isotopically leaf-conjugate affine Hirsch foliations 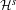${\mathcal{H}}^{s}$ and 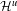${\mathcal{H}}^{u}$ on the orbit space of the wandering set of 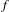$f$ (abbreviated to the wandering orbit space of 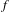$f$) by the stable and unstable manifolds of 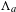$\unicode[STIX]{x1D6EC}_{a}$ and 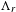$\unicode[STIX]{x1D6EC}_{r}$, respectively. Under this viewpoint, we build some close relationships between north–south Smale solenoid diffeomorphisms and Hirsch manifolds (the closed $3$-manifolds admitting two non-isotopically leaf-conjugate affine Hirsch foliations).

  • ∙ On the one hand, the union of the wandering orbit spaces is nearly in one-to-one correspondence with the union of Hirsch manifolds.

  • ∙ On the other hand, surprisingly, the topology of the wandering orbit space (Hirsch manifold) is nearly a complete invariant of north–south Smale solenoid diffeomorphisms up to semi-global conjugacy.

Moreover, as applications, we consider several more concrete questions. For instance, we prove that every diffeomorphism in many semi-global conjugacy classes of north–south Smale solenoid diffeomorphisms are not structurally stable.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 2 , February 2019 , pp. 531 - 553
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Block, L.. Diffeomorphisms obtained from endomorphisms. Trans. Amer. Math. Soc. 214 (1975), 403–413.Google Scholar
Bonatti, C. and Guelman, N.. Axiom A diffeomorphisms derived from Anosov flows. J. Mod. Dyn. 4(1) (2010), 1–63.Google Scholar
Bothe, H.. The ambient structure of expanding attractors. II. Solenoids in 3-manifolds. Math. Nachr. 112 (1983), 69–102.Google Scholar
Bothe, H.. The ambient structure of expanding attractors. I. Local triviality, tubular neighborhoods. Math. Nachr. 107 (1982), 327–348.Google Scholar
van Danzig, D.. Über topologisch homogene Kontinua. Fund. Math. 14 (1930), 102–105.Google Scholar
Jiang, B., Ni, Y. and Wang, S.. 3-manifolds that admit knotted solenoids as attractors. Trans. Amer. Math. Soc. 356 (2004), 4371–4382.Google Scholar
Ma, J. and Yu, B.. The realization of Smale solenoid type attractors in 3-manifolds. Topology Appl. 154(17) (2007), 3021–3031.Google Scholar
Morton, H. R.. Exchangeable braids. Low-dimensional Topology (Chelwood Gate, 1982) (London Mathematical Society Lecture Note Series, 95) . Cambridge University Press, Cambridge, 1985, pp. 86–105.Google Scholar
Robinson, C.. Dynamical Systems. Stability, Symbolic Dynamics, and Chaos (Studies in Advanced Mathematics) , 2nd edn. CRC Press, Boca Raton, FL, 1999.Google Scholar
Rudolph, L.. Special positions for surfaces bounded by closed braids. Rev. Mat. Iberoam. 1(3) (1985), 93–133.Google Scholar
Rudolph, L.. Isolated critical points of maps from ℝ4 to ℝ2 and a natural splitting of the Milnor number of a classical fibred link. II. Geometry and Topology (Athens, GA, 1985) (Lecture Notes in Pure and Applied Mathematics, 105) . Dekker, New York, 1987, pp. 251–263.Google Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. (N.S.) 73 (1967), 747–817.Google Scholar
Vietoris, L.. Uber den hoheren Zusammenhang kompakter Raume und eine Klasse von zusammenhangstreuen Abbildungen. Math. Ann. 97(1) (1927), 454–472 (in German).Google Scholar
Williams, R. F.. Expanding attractors. Publ. Math. Inst. Hautes Études Sci. 43 (1974), 169–203.Google Scholar
Yu, B.. Affine Hirsch foliations on $3$ -manifolds. Algebr. Geom. Topol. Preprint, 2016, to appear, arXiv:1604.03723.Google Scholar
Zhuzhoma, E. V. and Isaenkova, N. V.. On zero-dimensional solenoidal basic sets. Mat. Sb. 202(3) (2011), 47–68. Engl. Transl. Sb. Math. 202(3–4) (2011), 351–372.Google Scholar