Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
van Strien, Sebastian
1990.
Smooth linearization of hyperbolic fixed points without resonance conditions.
Journal of Differential Equations,
Vol. 85,
Issue. 1,
p.
66.
Dumortier, Freddy
1991.
Transition functions and moduli of stability for 3-dimensional homogeneous vector fields with a hyperbolic blowing-up.
Journal of Differential Equations,
Vol. 94,
Issue. 2,
p.
379.
Dumortier, F.
1991.
Structures in Dynamics - Finite Dimensional Deterministic Studies.
Vol. 2,
Issue. ,
p.
161.
Camacho, Maria Izabel Tavares
1992.
Genericity of hyperbolic homogeneous vector fields in R3.
Journal of Differential Equations,
Vol. 97,
Issue. 2,
p.
288.
Hadeler, K.P
1992.
Periodic solutions of homogeneous equations.
Journal of Differential Equations,
Vol. 95,
Issue. 1,
p.
183.
Alonso, Clementa
2002.
Topological equivalence for saddle connections.
Qualitative Theory of Dynamical Systems,
Vol. 3,
Issue. 2,
p.
309.
Alonso-González, Clementa
2005.
Topological equivalence for chains of saddle-connections.
Journal of Differential Equations,
Vol. 208,
Issue. 2,
p.
275.
ALONSO-GONZÁLEZ, CLEMENTA
2015.
Infinitesimal Hartman-Grobman Theorem in Dimension Three.
Anais da Academia Brasileira de Ciências,
Vol. 87,
Issue. 3,
p.
1499.
Zhang, Wenmeng
Lu, Kening
and
Zhang, Weinian
2017.
Differentiability of the conjugacy in the Hartman-Grobman Theorem.
Transactions of the American Mathematical Society,
Vol. 369,
Issue. 7,
p.
4995.
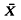 (which is defined on S2xℝ), and essentially means that there are no saddleconnections for
(which is defined on S2xℝ), and essentially means that there are no saddleconnections for  |S2×{0}.
|S2×{0}.