Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T04:00:45.579Z Has data issue: false hasContentIssue false
  • English
  • Français

Rokhlin towers and 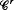closing for flows on T2

Published online by Cambridge University Press:  19 September 2008

C. R. Carroll
C. R. Carroll
Affiliation:
Department of Mathematics, Northwestern University, Evanston, IL 60208, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers the 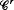closing problem, r≥2, for flows on T2 with finitely many singularities. We study the action of such flows on circles transverse to the flow, using Katznelson and Ornstein's picture of rigid rotations as Rokhlin towers. We are able to obtain closing on purely topological grounds for a large class of flows by means of perturbations which simply twist a flow along an embedded transverse circle (twist-perturbations). However, we give an example of a flow (with finitely many singularities) for which no 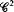small twist-perturbation yields closing; indeed such perturbations either leave the non-wandering set unchanged or else collapse it to the set of singularities.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 12 , Issue 4 , December 1992 , pp. 683 - 706
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Carroll, C.. The r-closing problem for flows on T2. PhD Thesis. University of California at Berkeley (1990).Google Scholar
[2]Cherry, T.. Analytic quasi-periodic curves of discontinuous type on a torus. Proc. London Math. Soc 44 (1938), 175–215.CrossRefGoogle Scholar
[3]Denjoy, A.. Sur les courbes définies par les equations différentielles à la surface du tore. J. Math. Pure Appl. 11 (1932), 333–375.Google Scholar
[4]Gardiner, C. J.. The structure of flows exhibiting non-trivial recurrence on two-dimensional manifolds. J. Diff. Equations 57 (1985), 138–158.CrossRefGoogle Scholar
[5]Gutierrez, C.. On the -closing lemma for flows on the torus T2. Ergod. Th. & Dynam. Sys. 6 (1986), 45–56.CrossRefGoogle Scholar
[6]Gutierrez, C.. Smoothing continuous flows on two-manifolds and recurrences. Ergod. Th. & Dynam. Syst. 6 (1986), 17–44.CrossRefGoogle Scholar
[7]Gutierrez, C.. A counter-example to a closing lemma. Ergod. Th. & Dynam. Sys. 7 (1987), 509–530.CrossRefGoogle Scholar
[8]Hardy, G. & Wright, E.. Introduction to the Theory of Numbers. Clarendon Press: Oxford, 5th ed (1979).Google Scholar
[9]Katznelson, V. & Ornstein, D.. The differentiability of the conjugation of certain diffeomorphisms of the circle. Ergod. Th. & Dynam. Sys. 9 (1989), 643–680.CrossRefGoogle Scholar
[10]Jiehua, Mai. A simpler proof of closing lemma. Scientia Sinica (Series A), (1986) 1020–1030.Google Scholar
[11]Martens, M., Strien, S. Van, Melo, W. De & Mendes, P.. On Cherry flows. Ergod. Th. & Dynam. Sys. 10 (1990), 531–554.CrossRefGoogle Scholar
[12]Pugh, C. & Robinson, C.. The -closing lemma, including Hamiltonians. Ergod. Th. & Dynam. Sys. 3 (1983), 261–313.CrossRefGoogle Scholar
[13]Pugh, C.. Against the Closing Lemma. J. Diff. Eq. 17 (1973), 435–443.CrossRefGoogle Scholar
[14]Yoccoz, J.. II n'y a pas de contre-exemple de Denjoy analytique. C. R. Acad. Sc. Paris 298 Série 1, n.7 (1984), 141–144.Google Scholar