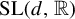1. Introduction
It is often difficult to rigorously determine the pseudorandom properties of a given sequence of real numbers modulo one, including even the simplest second-order correlation functions. In the present paper, we consider the problem in higher dimension and construct an explicit sequence of points
![]() $\boldsymbol {\upsilon }_1,\boldsymbol {\upsilon }_2,\boldsymbol {\upsilon }_3,\ldots $
on the unit sphere
$\boldsymbol {\upsilon }_1,\boldsymbol {\upsilon }_2,\boldsymbol {\upsilon }_3,\ldots $
on the unit sphere
![]() $\mathbb {S}^{d-1}$
whose two-point statistics converge to that of a Poisson point process. This sequence is given by the unit vectors
$\mathbb {S}^{d-1}$
whose two-point statistics converge to that of a Poisson point process. This sequence is given by the unit vectors
![]() $\boldsymbol {\upsilon }_j=\| \mathbf {y}_j \|^{-1} \mathbf {y}_j$
representing the directions of vectors
$\boldsymbol {\upsilon }_j=\| \mathbf {y}_j \|^{-1} \mathbf {y}_j$
representing the directions of vectors
![]() $\mathbf {y}_j$
in a fixed affine lattice in
$\mathbf {y}_j$
in a fixed affine lattice in
![]() $\mathbb {R}^d$
of unit covolume. Here the
$\mathbb {R}^d$
of unit covolume. Here the
![]() $\mathbf {y}_j$
are listed in increasing length
$\mathbf {y}_j$
are listed in increasing length
![]() $\|\mathbf {y}_j\|$
, where
$\|\mathbf {y}_j\|$
, where
![]() $\| \,\cdot \,\|$
denotes the Euclidean norm. If there are two or more vectors of the same length, we take them in arbitrary order (our results will not depend on the choice made). If there are several lattice points with the same direction, they will appear repeatedly in the sequence. Our approach extends the results of [Reference El-Baz, Marklof and VinogradovEMV15], which in turn builds on [Reference Marklof and StrömbergssonMS10], from
$\| \,\cdot \,\|$
denotes the Euclidean norm. If there are two or more vectors of the same length, we take them in arbitrary order (our results will not depend on the choice made). If there are several lattice points with the same direction, they will appear repeatedly in the sequence. Our approach extends the results of [Reference El-Baz, Marklof and VinogradovEMV15], which in turn builds on [Reference Marklof and StrömbergssonMS10], from
![]() $d=2$
to higher dimensions. We are furthermore able to relax the Diophantine hypotheses imposed in [Reference El-Baz, Marklof and VinogradovEMV15].
$d=2$
to higher dimensions. We are furthermore able to relax the Diophantine hypotheses imposed in [Reference El-Baz, Marklof and VinogradovEMV15].
A sequence
![]() $(\boldsymbol {\upsilon }_j)_{j=1}^\infty $
on
$(\boldsymbol {\upsilon }_j)_{j=1}^\infty $
on
![]() $\mathbb {S}^{d-1}$
is called uniformly distributed if for any set
$\mathbb {S}^{d-1}$
is called uniformly distributed if for any set
![]() $\mathcal {D}\subseteq \mathbb {S}^{d-1}$
with
$\mathcal {D}\subseteq \mathbb {S}^{d-1}$
with
![]() $\operatorname {vol}_{\mathbb {S}^{d-1}}(\partial \mathcal {D})=0$
, we have that
$\operatorname {vol}_{\mathbb {S}^{d-1}}(\partial \mathcal {D})=0$
, we have that
 $$ \begin{align*} \lim_{N\to\infty} \frac{1}{N} \#\{ j \leq N : \boldsymbol{\upsilon}_j \in\mathcal{D} \} = \frac{\operatorname{vol}_{\mathbb{S}^{d-1}}(\mathcal{D})}{V_{\mathbb{S}^{d-1}}}, \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty} \frac{1}{N} \#\{ j \leq N : \boldsymbol{\upsilon}_j \in\mathcal{D} \} = \frac{\operatorname{vol}_{\mathbb{S}^{d-1}}(\mathcal{D})}{V_{\mathbb{S}^{d-1}}}, \end{align*} $$
where
![]() $V_{\mathbb {S}^{d-1}}=\operatorname {vol}_{\mathbb {S}^{d-1}}(\mathbb {S}^{d-1})$
. The pair correlation function of the partial sequence
$V_{\mathbb {S}^{d-1}}=\operatorname {vol}_{\mathbb {S}^{d-1}}(\mathbb {S}^{d-1})$
. The pair correlation function of the partial sequence
![]() $(\boldsymbol {\upsilon }_j)_{j=1}^N$
is defined as
$(\boldsymbol {\upsilon }_j)_{j=1}^N$
is defined as
where
![]() $c_d= V_{\mathbb {S}^{d-1}}^{-{1}/({d-1})}$
and
$c_d= V_{\mathbb {S}^{d-1}}^{-{1}/({d-1})}$
and
![]() $\mathbf {d}_{\mathbb {S}^{d-1}}$
is the standard geodesic distance for the unit sphere
$\mathbf {d}_{\mathbb {S}^{d-1}}$
is the standard geodesic distance for the unit sphere
![]() $\mathbb {S}^{d-1}$
. The scaling by
$\mathbb {S}^{d-1}$
. The scaling by
![]() $c_d N^{{1}/({d-1})}$
ensures we are measuring correlations in units where the mean density of points is one (note that the scaled sphere
$c_d N^{{1}/({d-1})}$
ensures we are measuring correlations in units where the mean density of points is one (note that the scaled sphere
![]() $c_d N^{{1}/({d-1})}\mathbb {S}^{d-1}$
has volume N). The function
$c_d N^{{1}/({d-1})}\mathbb {S}^{d-1}$
has volume N). The function
![]() $R^2_N(s)$
is known as Ripley’s K-function in the statistical literature.
$R^2_N(s)$
is known as Ripley’s K-function in the statistical literature.
We say the pair correlation of the sequence
![]() $(\boldsymbol {\upsilon }_j)_{j=1}^\infty $
is Poissonian if for any
$(\boldsymbol {\upsilon }_j)_{j=1}^\infty $
is Poissonian if for any
![]() $s>0$
,
$s>0$
,
 $$ \begin{align} {\lim_{N\to \infty }R^2_N(s)=\frac{\pi^{({d-1})/{2}} s^{d-1}}{\Gamma(({d+1})/{2})},} \end{align} $$
$$ \begin{align} {\lim_{N\to \infty }R^2_N(s)=\frac{\pi^{({d-1})/{2}} s^{d-1}}{\Gamma(({d+1})/{2})},} \end{align} $$
which is the volume of a ball in
![]() $\mathbb {R}^{d-1}$
of radius s. This limit holds for example almost surely for a sequence of independent and uniformly distributed random points on
$\mathbb {R}^{d-1}$
of radius s. This limit holds for example almost surely for a sequence of independent and uniformly distributed random points on
![]() $\mathbb {S}^{d-1}$
. It coincides with the pair correlation function of a Poisson point process in
$\mathbb {S}^{d-1}$
. It coincides with the pair correlation function of a Poisson point process in
![]() $\mathbb {R}^{d-1}$
of intensity one; hence the term ‘Poissoninan’.
$\mathbb {R}^{d-1}$
of intensity one; hence the term ‘Poissoninan’.
Every affine lattice of unit covolume can be explicitly written as
![]() $\mathcal {L}_{\boldsymbol {\xi }}=(\mathbb {Z}^d+\boldsymbol {\xi })M_0$
, where
$\mathcal {L}_{\boldsymbol {\xi }}=(\mathbb {Z}^d+\boldsymbol {\xi })M_0$
, where
![]() $\boldsymbol {\xi }\in \mathbb {R}^d$
and
$\boldsymbol {\xi }\in \mathbb {R}^d$
and
![]() $M_0\in G=\operatorname {SL}(d,\mathbb {R})$
. For integer shift
$M_0\in G=\operatorname {SL}(d,\mathbb {R})$
. For integer shift
![]() $\boldsymbol {\xi }\in \mathbb {Z}^d$
, we obtain the underlying lattice
$\boldsymbol {\xi }\in \mathbb {Z}^d$
, we obtain the underlying lattice
![]() $\mathcal {L}=\mathbb {Z}^d M_0$
. It follows from classical asymptotics for the number of affine lattice points in expanding sectors with a fixed opening angle that the sequence of directions is uniformly distributed on
$\mathcal {L}=\mathbb {Z}^d M_0$
. It follows from classical asymptotics for the number of affine lattice points in expanding sectors with a fixed opening angle that the sequence of directions is uniformly distributed on
![]() $\mathbb {S}^{d-1}$
for any shift
$\mathbb {S}^{d-1}$
for any shift
![]() $\boldsymbol {\xi }\in \mathbb {R}^d$
.
$\boldsymbol {\xi }\in \mathbb {R}^d$
.
It is an interesting observation that a Poissonian pair correlation implies uniform distribution on general compact manifolds [Reference MarklofM20]. This fact was first proved in the case of
![]() $\mathbb {S}^{1}$
by Aistleitner, Lachmann and Pausinger [Reference Aistleitner, Lachmann and PausingerALP18], and independently by Larcher and Stockinger [Reference Larcher and StockingerLS20]. For the convergence of the pair correlation function, we will however, unlike the case of uniform distribution, require Diophantine conditions on the lattice shift
$\mathbb {S}^{1}$
by Aistleitner, Lachmann and Pausinger [Reference Aistleitner, Lachmann and PausingerALP18], and independently by Larcher and Stockinger [Reference Larcher and StockingerLS20]. For the convergence of the pair correlation function, we will however, unlike the case of uniform distribution, require Diophantine conditions on the lattice shift
![]() $\boldsymbol {\xi }$
. For
$\boldsymbol {\xi }$
. For
![]() $\kappa \ge d$
, we say that
$\kappa \ge d$
, we say that
![]() $\boldsymbol {\xi }\in \mathbb {R}^d$
is Diophantine of type
$\boldsymbol {\xi }\in \mathbb {R}^d$
is Diophantine of type
![]() $\kappa $
if there exists
$\kappa $
if there exists
![]() $C_\kappa>0$
such that
$C_\kappa>0$
such that
for any
![]() $\mathbf {m}\in \mathbb {Z}^d\setminus \{0\}$
, where
$\mathbf {m}\in \mathbb {Z}^d\setminus \{0\}$
, where
![]() $|\cdot |$
denotes the supremum norm of
$|\cdot |$
denotes the supremum norm of
![]() $\mathbb {R}^d$
and
$\mathbb {R}^d$
and
![]() $|\cdot |_{\mathbb {Z}}$
denotes the supremum distance from
$|\cdot |_{\mathbb {Z}}$
denotes the supremum distance from
![]() $0\in \mathbb {T}^d$
. It is known that Lebesgue-almost all
$0\in \mathbb {T}^d$
. It is known that Lebesgue-almost all
![]() $\boldsymbol {\xi }\in \mathbb {R}^d$
are of type
$\boldsymbol {\xi }\in \mathbb {R}^d$
are of type
![]() $\kappa $
for any
$\kappa $
for any
![]() $\kappa>d$
. We will in fact only require a milder Diophantine condition. Define the function
$\kappa>d$
. We will in fact only require a milder Diophantine condition. Define the function
![]() $ \zeta :\mathbb {R}^d \times \mathbb {R}_{>0}\to \mathbb {N}$
by
$ \zeta :\mathbb {R}^d \times \mathbb {R}_{>0}\to \mathbb {N}$
by
 $$ \begin{align} {\zeta(\boldsymbol{\xi},T):=\min\bigg\{N\in\mathbb{N}: \min_{\substack{\mathbf{m}\in\mathbb{Z}^d\setminus\{0\}\\ 0<|\mathbf{m}|\leq N}}|\boldsymbol{\xi}\cdot\mathbf{m}|_{\mathbb{Z}}\leq \frac{1}{T}\bigg\}.} \end{align} $$
$$ \begin{align} {\zeta(\boldsymbol{\xi},T):=\min\bigg\{N\in\mathbb{N}: \min_{\substack{\mathbf{m}\in\mathbb{Z}^d\setminus\{0\}\\ 0<|\mathbf{m}|\leq N}}|\boldsymbol{\xi}\cdot\mathbf{m}|_{\mathbb{Z}}\leq \frac{1}{T}\bigg\}.} \end{align} $$
In view of Dirichlet’s pigeon hole principle, we have that
![]() $\zeta (\boldsymbol {\xi },T)\leq T^{1/d}$
and, if
$\zeta (\boldsymbol {\xi },T)\leq T^{1/d}$
and, if
![]() $\boldsymbol {\xi }$
is of Diophantine type
$\boldsymbol {\xi }$
is of Diophantine type
![]() $\kappa \geq d$
, then
$\kappa \geq d$
, then
![]() $\zeta (\boldsymbol {\xi },T)> (C_\kappa T)^{{1}/{\kappa }}$
.
$\zeta (\boldsymbol {\xi },T)> (C_\kappa T)^{{1}/{\kappa }}$
.
We say
![]() $\boldsymbol {\xi }\in \mathbb {R}^d$
is
$\boldsymbol {\xi }\in \mathbb {R}^d$
is
![]() $(\rho ,\mu ,\nu )$
-vaguely Diophantine if
$(\rho ,\mu ,\nu )$
-vaguely Diophantine if
 $$ \begin{align*}\sum_{l=1}^{\infty}l^\rho\, 2^{\mu}\zeta(\boldsymbol{\xi},2^{l-1})^{-\nu}<\infty .\end{align*} $$
$$ \begin{align*}\sum_{l=1}^{\infty}l^\rho\, 2^{\mu}\zeta(\boldsymbol{\xi},2^{l-1})^{-\nu}<\infty .\end{align*} $$
Thus, if
![]() $\boldsymbol {\xi }$
is Diophantine type
$\boldsymbol {\xi }$
is Diophantine type
![]() $\kappa $
, then it is also
$\kappa $
, then it is also
![]() $(\rho ,\mu ,\nu )$
-vaguely Diophantine for
$(\rho ,\mu ,\nu )$
-vaguely Diophantine for
![]() ${\kappa \mu <\nu }$
. If
${\kappa \mu <\nu }$
. If
![]() $\boldsymbol {\xi }$
satisfies the weaker Brjuno Diophantine condition [Reference Bounemoura and FéjozBF19, Reference Lopes Dias and GaivãoLDG19], then it is
$\boldsymbol {\xi }$
satisfies the weaker Brjuno Diophantine condition [Reference Bounemoura and FéjozBF19, Reference Lopes Dias and GaivãoLDG19], then it is
![]() $(\rho ,0,\nu )$
-vaguely Diophantine for
$(\rho ,0,\nu )$
-vaguely Diophantine for
![]() $0\leq \rho <\nu -1$
(see Appendix A).
$0\leq \rho <\nu -1$
(see Appendix A).
Theorem 1.1. Let
![]() $d\geq 2$
and
$d\geq 2$
and
![]() $\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
; furthermore, if
$\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
; furthermore, if
![]() $d=2$
, assume that
$d=2$
, assume that
![]() $\boldsymbol {\xi }$
is
$\boldsymbol {\xi }$
is
![]() $(0,0,2)$
-vaguely Diophantine. Then the pair correlation function of the sequence
$(0,0,2)$
-vaguely Diophantine. Then the pair correlation function of the sequence
![]() $(\boldsymbol {\upsilon }_j)_{j=1}^\infty $
of directions is Poissonian.
$(\boldsymbol {\upsilon }_j)_{j=1}^\infty $
of directions is Poissonian.
We note that the hypothesis on
![]() $\boldsymbol {\xi }$
(in the case
$\boldsymbol {\xi }$
(in the case
![]() $d=2$
) is satisfied for all Brjuno vectors and, thus, in particular for Diophantine vectors of any type. In Appendix B, we prove that there is a set of second Baire category of
$d=2$
) is satisfied for all Brjuno vectors and, thus, in particular for Diophantine vectors of any type. In Appendix B, we prove that there is a set of second Baire category of
![]() $\boldsymbol {\xi }\in \mathbb {R}^2\setminus \mathbb {Q}^2$
for which the pair correlation function diverges. This shows that the Diophantine condition is indeed required.
$\boldsymbol {\xi }\in \mathbb {R}^2\setminus \mathbb {Q}^2$
for which the pair correlation function diverges. This shows that the Diophantine condition is indeed required.
The pair correlation function also exists for
![]() $\boldsymbol {\xi }\in \mathbb {Q}^d$
if
$\boldsymbol {\xi }\in \mathbb {Q}^d$
if
![]() $d\geq 3$
and is closely related to the two-point statistics of multi-dimensional Farey sequences [Reference Boca and ZaharescuBZ05, Reference Marklof, Eichelsbacher, Elsner, Kösters, Löwe, Merkl and RollesM13] and visible lattice points [Reference Boca, Cobeli and ZahrescuBCZ00, Reference Marklof and StrömbergssonMS10]. The deeper reason why we see a Poisson pair correlation for
$d\geq 3$
and is closely related to the two-point statistics of multi-dimensional Farey sequences [Reference Boca and ZaharescuBZ05, Reference Marklof, Eichelsbacher, Elsner, Kösters, Löwe, Merkl and RollesM13] and visible lattice points [Reference Boca, Cobeli and ZahrescuBCZ00, Reference Marklof and StrömbergssonMS10]. The deeper reason why we see a Poisson pair correlation for
![]() $\boldsymbol {\xi }\notin \mathbb {Q}^d$
is that the limit distribution is expressed through the Haar measure on the semi-direct product group
$\boldsymbol {\xi }\notin \mathbb {Q}^d$
is that the limit distribution is expressed through the Haar measure on the semi-direct product group
![]() $\operatorname {SL}(d,\mathbb {R}) \ltimes \mathbb {R}^d$
, where the averages over double-lattice sums reduce to Siegel’s mean value formula; cf. Proposition 7.1 and [Reference El-Baz, Marklof and VinogradovEMV15, Proposition 14]. In the case of
$\operatorname {SL}(d,\mathbb {R}) \ltimes \mathbb {R}^d$
, where the averages over double-lattice sums reduce to Siegel’s mean value formula; cf. Proposition 7.1 and [Reference El-Baz, Marklof and VinogradovEMV15, Proposition 14]. In the case of
![]() $\boldsymbol {\xi }\in \mathbb {Q}^d$
, we need to apply Rogers’ formulae that exhibit non-trivial correlations in the lattice sums, which explains the non-Poissonian correlations in this case. This is also the reason why three-point and higher-order correlation functions for directions in affine lattices with
$\boldsymbol {\xi }\in \mathbb {Q}^d$
, we need to apply Rogers’ formulae that exhibit non-trivial correlations in the lattice sums, which explains the non-Poissonian correlations in this case. This is also the reason why three-point and higher-order correlation functions for directions in affine lattices with
![]() $\boldsymbol {\xi }\notin \mathbb {Q}^d$
are non-Poissonian. Fine-scale statistics of directions have also been studied in the context of quasicrystals [Reference Baake, Götze, Huck and JakobiBGHJ14, Reference HammarhjelmH22, Reference Marklof and StrömbergssonMS15].
$\boldsymbol {\xi }\notin \mathbb {Q}^d$
are non-Poissonian. Fine-scale statistics of directions have also been studied in the context of quasicrystals [Reference Baake, Götze, Huck and JakobiBGHJ14, Reference HammarhjelmH22, Reference Marklof and StrömbergssonMS15].
It is worth highlighting that in the analogous problem of directions in hyperbolic lattices, the pair correlation statistics are not Poissonian; see [Reference Marklof and VinogradovMV18] and references therein.
Theorem 1.1 provides an example of a deterministic sequence in higher dimension whose pair correlation density is Poissonian. Other local statistics, however, deviate from the Poisson distribution in other statistical tests, as shown in [Reference Marklof and StrömbergssonMS10]. By deterministic, we mean here that convergence is proved not just almost surely or in probability, but for a fixed, explicit sequence. An interesting non-Poisson random point process with Poissonian pair correlation is discussed in [Reference Baddeley and SilvermanBS84].
Theorem 1.1 generalizes results of [Reference El-Baz, Marklof and VinogradovEMV15] for two-dimensional affine lattices and under a stronger Diophantine condition on
![]() $\boldsymbol {\xi }$
, as well as earlier work by Boca and Zaharescu [Reference Boca and ZaharescuBZ06] that was limited to almost every
$\boldsymbol {\xi }$
, as well as earlier work by Boca and Zaharescu [Reference Boca and ZaharescuBZ06] that was limited to almost every
![]() $\boldsymbol {\xi }\in \mathbb {R}^2$
. Other examples of deterministic sequences with Poissonian pair correlation in one dimension include
$\boldsymbol {\xi }\in \mathbb {R}^2$
. Other examples of deterministic sequences with Poissonian pair correlation in one dimension include
![]() $\sqrt n \bmod 1$
(excluding n that are perfect squares) [Reference Elkies and McMullenEM04, Reference El-Baz, Marklof and VinogradovEMV15b] and the recent paper by Lutsko, Sourmelidis and Technau [Reference Lutsko, Sourmelidis and TechnauLST21] on
$\sqrt n \bmod 1$
(excluding n that are perfect squares) [Reference Elkies and McMullenEM04, Reference El-Baz, Marklof and VinogradovEMV15b] and the recent paper by Lutsko, Sourmelidis and Technau [Reference Lutsko, Sourmelidis and TechnauLST21] on
![]() $\alpha n^\theta \bmod 1$
that holds for every
$\alpha n^\theta \bmod 1$
that holds for every
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $\theta \leq 1/3$
. Sequences such as
$\theta \leq 1/3$
. Sequences such as
![]() $\alpha n^2\bmod 1$
[Reference Rudnick and SarnakRS98] or
$\alpha n^2\bmod 1$
[Reference Rudnick and SarnakRS98] or
![]() $\alpha 2^n\bmod 1$
[Reference Rudnick and ZaharescuRZ99] have Poissonian pair correlation for almost every
$\alpha 2^n\bmod 1$
[Reference Rudnick and ZaharescuRZ99] have Poissonian pair correlation for almost every
![]() $\alpha $
, but with no explicit instances of
$\alpha $
, but with no explicit instances of
![]() $\alpha $
currently known. For more references on recent developments on metric pair correlation problems, we refer the reader to [Reference Aistleitner, El-Baz and MunschAEM21, Reference Larcher and StockingerLS20b] and references therein.
$\alpha $
currently known. For more references on recent developments on metric pair correlation problems, we refer the reader to [Reference Aistleitner, El-Baz and MunschAEM21, Reference Larcher and StockingerLS20b] and references therein.
Finally, we mention work of Bourgain, Rudnick and Sarnak [Reference Bourgain, Rudnick, Sarnak, Hardin, Lubinsky and SimanekBRS16, Reference Bourgain, Rudnick and SarnakBRS17], who considered the fine-scale statistics of lattice points (without a shift) on large spheres, rather than radially projected points as in our setting. Remarkably, in dimension two, Kurlberg and Lester have recently been able to prove that all correlation functions converge to Poisson along density-one subsequences of eligible radii [Reference Kurlberg and LesterKL22].
The next section will recall the convergence in distribution for the directions in affine lattices from [Reference Marklof and StrömbergssonMS10], and then state an extension to convergence of mixed moments (Theorem 2.2), which is the main result of this paper. An application of the Siegel mean value formula gives explicit expressions for all second-order statistics and in particular shows that the pair correlation function is Poissonian (Corollaries 2.3 and 2.4). These results thus immediately imply Theorem 1.1. Section 3 introduces the space of affine lattices. In §5, we prove escape-of-mass estimates for spherical averages that allow us to pass from convergence in distribution to convergence of moments. Sections 6 and 7 supply the proofs of our Main Lemma, which immediately implies Theorem 2.2, and Corollaries 2.3 and 2.4, respectively.
2. Limit distribution and higher moments
We consider the set
![]() $\mathcal {P}_T$
of affine lattice points
$\mathcal {P}_T$
of affine lattice points
![]() $y\in \mathcal {L}_{\boldsymbol {\xi }}$
inside the ball of radius
$y\in \mathcal {L}_{\boldsymbol {\xi }}$
inside the ball of radius
![]() $\mathcal {B}_T^d$
or, more generally,
$\mathcal {B}_T^d$
or, more generally,
![]() $\mathcal {P}_{c,T}$
the lattice points in the spherical shell
$\mathcal {P}_{c,T}$
the lattice points in the spherical shell
The well-known asymptotics for the number of lattice points in a large ball yields for
![]() $T\to \infty $
,
$T\to \infty $
,
For
![]() $\sigma>0$
and
$\sigma>0$
and
![]() $\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}$
, we define
$\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}$
, we define
![]() $\mathfrak {D}_{c,T}(\sigma ,\boldsymbol {\upsilon })\subseteq \mathbb {S}^{d-1}$
to be the open disc with centre
$\mathfrak {D}_{c,T}(\sigma ,\boldsymbol {\upsilon })\subseteq \mathbb {S}^{d-1}$
to be the open disc with centre
![]() $\boldsymbol {\upsilon }$
and volume
$\boldsymbol {\upsilon }$
and volume
Then the radius of
![]() $\mathfrak {D}_{c,T}(\sigma ,\boldsymbol {\upsilon })$
is
$\mathfrak {D}_{c,T}(\sigma ,\boldsymbol {\upsilon })$
is
![]() $\asymp T^{-{d}/({d-1})}$
, and for
$\asymp T^{-{d}/({d-1})}$
, and for
![]() $T\to \infty $
,
$T\to \infty $
,
 $$ \begin{align*} \frac{\operatorname{vol}_{\mathbb{S}^{d-1}}(\mathfrak{D}_{c,T}(\sigma,\boldsymbol{\upsilon}))}{V_{\mathbb{S}^{d-1}}} \sim \frac{\sigma}{\#\mathcal{P}_{c,T}}. \end{align*} $$
$$ \begin{align*} \frac{\operatorname{vol}_{\mathbb{S}^{d-1}}(\mathfrak{D}_{c,T}(\sigma,\boldsymbol{\upsilon}))}{V_{\mathbb{S}^{d-1}}} \sim \frac{\sigma}{\#\mathcal{P}_{c,T}}. \end{align*} $$
Thus,
![]() $\sigma $
measures the disc’s volume in terms of the average density of points on the sphere; this scale is compatible with the one introduced above for the pair correlation function.
$\sigma $
measures the disc’s volume in terms of the average density of points on the sphere; this scale is compatible with the one introduced above for the pair correlation function.
We define the counting function
for the number of affine lattice points whose direction is contained in
![]() $\mathfrak {D}_{c,T}(\sigma ,\boldsymbol {\upsilon })$
. Note that on average over
$\mathfrak {D}_{c,T}(\sigma ,\boldsymbol {\upsilon })$
. Note that on average over
![]() $\boldsymbol {\upsilon }$
, uniform distribution implies (cf. [Reference Marklof and StrömbergssonMS10, §2.3]) that for any Borel probability measure
$\boldsymbol {\upsilon }$
, uniform distribution implies (cf. [Reference Marklof and StrömbergssonMS10, §2.3]) that for any Borel probability measure
![]() $\unicode{x3bb} $
on
$\unicode{x3bb} $
on
![]() $\mathbb {S}^{d-1}$
with continuous density, we have
$\mathbb {S}^{d-1}$
with continuous density, we have
This says that the expected number of affine lattice points, with direction contained in
![]() $\mathfrak {D}_{c,T}(\sigma ,\boldsymbol {\upsilon })$
for random
$\mathfrak {D}_{c,T}(\sigma ,\boldsymbol {\upsilon })$
for random
![]() $\boldsymbol {\upsilon }$
, is
$\boldsymbol {\upsilon }$
, is
![]() $\sigma $
.
$\sigma $
.
We recall the following result from [Reference Marklof and StrömbergssonMS10], which provides the full limit distribution of
![]() $\mathcal {N}_{c,T}(\sigma , \boldsymbol {\upsilon })$
with random
$\mathcal {N}_{c,T}(\sigma , \boldsymbol {\upsilon })$
with random
![]() $\boldsymbol {\upsilon }$
distributed according to a general Borel probability measure
$\boldsymbol {\upsilon }$
distributed according to a general Borel probability measure
![]() $\unicode{x3bb} $
.
$\unicode{x3bb} $
.
Theorem 2.1. [Reference Marklof and StrömbergssonMS10]
For
![]() $\underline {\sigma }=(\sigma _1,\ldots ,\sigma _m)\in \mathbb {R}_{>0}^m$
, there is a probability distribution
$\underline {\sigma }=(\sigma _1,\ldots ,\sigma _m)\in \mathbb {R}_{>0}^m$
, there is a probability distribution
![]() $E_{c,\boldsymbol {\xi }}(\cdot , \underline {\sigma })$
on
$E_{c,\boldsymbol {\xi }}(\cdot , \underline {\sigma })$
on
![]() $\mathbb {Z}^m_{\geq 0}$
such that, for any
$\mathbb {Z}^m_{\geq 0}$
such that, for any
![]() $\underline {r}=(r_1,\ldots ,r_m)\in \mathbb {Z}^m_{\geq 0}$
and any Borel probability measure
$\underline {r}=(r_1,\ldots ,r_m)\in \mathbb {Z}^m_{\geq 0}$
and any Borel probability measure
![]() $\unicode{x3bb} $
on
$\unicode{x3bb} $
on
![]() $\mathbb {S}^{d-1}$
, absolutely continuous with respect to Lebesgue,
$\mathbb {S}^{d-1}$
, absolutely continuous with respect to Lebesgue,
The limit distribution satisfies the following properties, cf. §4:
-
(a)
 $E_{c,\boldsymbol {\xi }}(\underline {r},\underline {\sigma })$
is independent of
$E_{c,\boldsymbol {\xi }}(\underline {r},\underline {\sigma })$
is independent of
 $\unicode{x3bb} $
and
$\unicode{x3bb} $
and
 $\mathcal {L}$
;
$\mathcal {L}$
; -
(b)
 $\sum _{\underline {r}\in \mathbb {Z}_{\ge 0}^m}r_jE_{c,\boldsymbol {\xi }}(\underline {r},\underline {\sigma })=\sum _{r=0}^{\infty }rE_{c,\boldsymbol {\xi }}(r,\sigma _j)=\sigma _j$
for any
$\sum _{\underline {r}\in \mathbb {Z}_{\ge 0}^m}r_jE_{c,\boldsymbol {\xi }}(\underline {r},\underline {\sigma })=\sum _{r=0}^{\infty }rE_{c,\boldsymbol {\xi }}(r,\sigma _j)=\sigma _j$
for any
 $j\leq m$
;
$j\leq m$
; -
(c) for
 $\boldsymbol {\xi }\in \mathbb {Q}^d$
,
$\boldsymbol {\xi }\in \mathbb {Q}^d$
,
 $\sum _{\underline {r}\in \mathbb {Z}_{\ge 0}^m} \|\underline {r}\|^s E_{c,\boldsymbol {\xi }}(\underline {r},\underline {\sigma }) < \infty $
for
$\sum _{\underline {r}\in \mathbb {Z}_{\ge 0}^m} \|\underline {r}\|^s E_{c,\boldsymbol {\xi }}(\underline {r},\underline {\sigma }) < \infty $
for
 $0\le s<d$
and
$0\le s<d$
and
 $=\infty $
for
$=\infty $
for
 $s\ge d$
.
$s\ge d$
. -
(d) for
 $\boldsymbol {\xi }\notin \mathbb {Q}^d$
,
$\boldsymbol {\xi }\notin \mathbb {Q}^d$
,
 $E_{c,\boldsymbol {\xi }}(\underline {r},\underline {\sigma })=:E_{c}(\underline {r},\underline {\sigma })$
is independent of
$E_{c,\boldsymbol {\xi }}(\underline {r},\underline {\sigma })=:E_{c}(\underline {r},\underline {\sigma })$
is independent of
 $\boldsymbol {\xi }$
;
$\boldsymbol {\xi }$
; -
(e) for
 $\boldsymbol {\xi }\notin \mathbb {Q}^d$
,
$\boldsymbol {\xi }\notin \mathbb {Q}^d$
,
 $\sum _{\underline {r}\in \mathbb {Z}_{\ge 0}^m} \|\underline {r}\|^s E_{c}(\underline {r},\underline {\sigma }) < \infty $
for
$\sum _{\underline {r}\in \mathbb {Z}_{\ge 0}^m} \|\underline {r}\|^s E_{c}(\underline {r},\underline {\sigma }) < \infty $
for
 $0\le s<d+1$
and
$0\le s<d+1$
and
 $=\infty $
for
$=\infty $
for
 $s\ge d+1$
.
$s\ge d+1$
.
A key ingredient of the proof of Theorem 2.1 is Ratner’s measure classification theorem, which allows one to prove equidistribution of horospheres embedded in the space of affine lattices. An effective version of this statement was established only recently [Reference KimK21].
Let us now turn to the main outcome of the present investigation, which extends the results of [Reference El-Baz, Marklof and VinogradovEMV15] to arbitrary dimension. For
![]() $\sigma _1,\ldots ,\sigma _m>0$
,
$\sigma _1,\ldots ,\sigma _m>0$
,
![]() $\unicode{x3bb} $
a Borel probability measure on
$\unicode{x3bb} $
a Borel probability measure on
![]() $\mathbb {S}^{d-1}$
and
$\mathbb {S}^{d-1}$
and
![]() $\underline {z}=(z_1,\ldots ,z_m)\in \mathbb {C}^m$
, let
$\underline {z}=(z_1,\ldots ,z_m)\in \mathbb {C}^m$
, let
We denote the positive real part of
![]() $z\in \mathbb {C}$
by
$z\in \mathbb {C}$
by
![]() $\operatorname {Re}_+(z):=\max \{\operatorname {Re}(z),0\}$
.
$\operatorname {Re}_+(z):=\max \{\operatorname {Re}(z),0\}$
.
The following is the principal theorem of this paper.
Theorem 2.2. Let
![]() $\sigma _1,\ldots ,\sigma _m>0$
and
$\sigma _1,\ldots ,\sigma _m>0$
and
![]() $\unicode{x3bb} $
a Borel probability measure on
$\unicode{x3bb} $
a Borel probability measure on
![]() $\mathbb {S}^{d-1}$
with continuous density. Choose
$\mathbb {S}^{d-1}$
with continuous density. Choose
![]() $\boldsymbol {\xi }\in \mathbb {R}^d$
and
$\boldsymbol {\xi }\in \mathbb {R}^d$
and
![]() $\underline {z}=(z_1,\ldots ,z_m)\in \mathbb {C}^m$
, such that one of the following hypotheses holds:
$\underline {z}=(z_1,\ldots ,z_m)\in \mathbb {C}^m$
, such that one of the following hypotheses holds:
-
(A1)
 $\operatorname {Re}_+(z_1)+\cdots +\operatorname {Re}_+(z_m)<d;$
$\operatorname {Re}_+(z_1)+\cdots +\operatorname {Re}_+(z_m)<d;$
-
(A2)
 $\eta :=\operatorname {Re}_+(z_1)+\cdots +\operatorname {Re}_+(z_m)<d+1$
and
$\eta :=\operatorname {Re}_+(z_1)+\cdots +\operatorname {Re}_+(z_m)<d+1$
and
 $\boldsymbol {\xi }$
is
$\boldsymbol {\xi }$
is
 $(0,\eta -2,2)$
-vaguely Diophantine if
$(0,\eta -2,2)$
-vaguely Diophantine if
 $d=2$
and
$d=2$
and
 $(d-1,\eta -d,1)$
-vaguely Diophantine if
$(d-1,\eta -d,1)$
-vaguely Diophantine if
 $d\geq 3$
.
$d\geq 3$
.
Then
 $$ \begin{align} {\lim_{T\to\infty}\mathbb{M}_\unicode{x3bb}(T,\underline{z})=\sum_{\underline{r}\in\mathbb{Z}_{\ge0}^m}(r_1+1)^{z_1}\cdots(r_m+1)^{z_m}E_{c,\boldsymbol{\xi}}(\underline{r},\underline{\sigma}).} \end{align} $$
$$ \begin{align} {\lim_{T\to\infty}\mathbb{M}_\unicode{x3bb}(T,\underline{z})=\sum_{\underline{r}\in\mathbb{Z}_{\ge0}^m}(r_1+1)^{z_1}\cdots(r_m+1)^{z_m}E_{c,\boldsymbol{\xi}}(\underline{r},\underline{\sigma}).} \end{align} $$
We note that if
![]() $\boldsymbol {\xi }$
is Diophantine of type
$\boldsymbol {\xi }$
is Diophantine of type
![]() $\kappa $
then under hypothesis (A2), we have
$\kappa $
then under hypothesis (A2), we have
![]() ${\eta <2+(2/\kappa )}$
if
${\eta <2+(2/\kappa )}$
if
![]() $d=2$
and
$d=2$
and
![]() $\eta <d+(1/\kappa )$
if
$\eta <d+(1/\kappa )$
if
![]() $d\geq 3$
. Thus, in particular for badly approximable
$d\geq 3$
. Thus, in particular for badly approximable
![]() $\boldsymbol {\xi }$
(where
$\boldsymbol {\xi }$
(where
![]() $\kappa =d$
), we have
$\kappa =d$
), we have
![]() $\eta <3$
if
$\eta <3$
if
![]() $d=2$
and
$d=2$
and
![]() $\eta <d+({1}/{d})$
if
$\eta <d+({1}/{d})$
if
![]() $d\geq 3$
.
$d\geq 3$
.
We define the restricted moments to explain the key step of the proof of Theorem 2.2:
 $$ \begin{align} {\mathbb{M}_\unicode{x3bb}^{(K)}(T,\underline{z}):=\int_{\max_j \mathcal{N}_{c,T}(\sigma_j,\boldsymbol{\upsilon})\leq K}(\mathcal{N}_{c,T}(\sigma_1,\boldsymbol{\upsilon})+1)^{z_1}\cdots(\mathcal{N}_{c,T}(\sigma_m,\boldsymbol{\upsilon})+1)^{z_m}\unicode{x3bb}(d\boldsymbol{\upsilon}).} \end{align} $$
$$ \begin{align} {\mathbb{M}_\unicode{x3bb}^{(K)}(T,\underline{z}):=\int_{\max_j \mathcal{N}_{c,T}(\sigma_j,\boldsymbol{\upsilon})\leq K}(\mathcal{N}_{c,T}(\sigma_1,\boldsymbol{\upsilon})+1)^{z_1}\cdots(\mathcal{N}_{c,T}(\sigma_m,\boldsymbol{\upsilon})+1)^{z_m}\unicode{x3bb}(d\boldsymbol{\upsilon}).} \end{align} $$
Then Theorem 2.1 implies that for any
![]() $K>0$
,
$K>0$
,
 $$ \begin{align} {\lim_{T\to\infty}\mathbb{M}_\unicode{x3bb}^{(K)}(T,\underline{z})=\sum_{\underline{r}\in\mathbb{Z}_{\ge0}^m, |\underline{r}|\leq K}(r_1+1)^{z_1}\cdots(r_m+1)^{z_m}E_{c,\boldsymbol{\xi}}(\underline{r},\underline{\sigma}),} \end{align} $$
$$ \begin{align} {\lim_{T\to\infty}\mathbb{M}_\unicode{x3bb}^{(K)}(T,\underline{z})=\sum_{\underline{r}\in\mathbb{Z}_{\ge0}^m, |\underline{r}|\leq K}(r_1+1)^{z_1}\cdots(r_m+1)^{z_m}E_{c,\boldsymbol{\xi}}(\underline{r},\underline{\sigma}),} \end{align} $$
where
![]() $|\underline {r}|:=\max _{1\leq j\leq m}r_m$
. Thus, for the proof of Theorem 2.2 it remains to show that under hypotheses (A1)–(A2),
$|\underline {r}|:=\max _{1\leq j\leq m}r_m$
. Thus, for the proof of Theorem 2.2 it remains to show that under hypotheses (A1)–(A2),
We will prove this in §6.
The following corollaries of Theorem 2.2 state that, in particular, the second moment and pair correlation converge and are Poisonnian.
Corollary 2.3. Let
![]() $\unicode{x3bb} $
be as in Theorem 2.2. Let
$\unicode{x3bb} $
be as in Theorem 2.2. Let
![]() $d\geq 2$
and
$d\geq 2$
and
![]() $\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
; furthermore, if
$\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
; furthermore, if
![]() $d=2$
, assume that
$d=2$
, assume that
![]() $\boldsymbol {\xi }$
is
$\boldsymbol {\xi }$
is
![]() $(0,0,2)$
-vaguely Diophantine. Then, for any
$(0,0,2)$
-vaguely Diophantine. Then, for any
![]() $\sigma _1,\sigma _2>0$
,
$\sigma _1,\sigma _2>0$
,
Let
![]() $N=N_c(T)$
be the number of points in
$N=N_c(T)$
be the number of points in
![]() $\mathcal {P}_{c,T}$
and let
$\mathcal {P}_{c,T}$
and let
![]() $\boldsymbol {\upsilon }_{j}=\|\mathbf {y}_j\|^{-1}\mathbf {y}_j\in \mathbb {S}^{d-1}$
be the directions of the vectors
$\boldsymbol {\upsilon }_{j}=\|\mathbf {y}_j\|^{-1}\mathbf {y}_j\in \mathbb {S}^{d-1}$
be the directions of the vectors
![]() $\mathbf {y}_j\in \mathcal {P}_{c,T}$
, with
$\mathbf {y}_j\in \mathcal {P}_{c,T}$
, with
![]() $j=1,\ldots ,N_c(T)$
. For
$j=1,\ldots ,N_c(T)$
. For
![]() ${f\in \operatorname {C}_0(\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}\times \mathbb {R})}$
(continuous, real-valued and with compact support), we define the two-point correlation function
${f\in \operatorname {C}_0(\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}\times \mathbb {R})}$
(continuous, real-valued and with compact support), we define the two-point correlation function
 $$ \begin{align} {R_N^2(f)=\frac{1}{N}\sum_{\substack{j_1,j_2=1\\ j_1\neq j_2}}^N f(\boldsymbol{\upsilon}_{j_1},\boldsymbol{\upsilon}_{j_2}, c_d N^{{1}/({d-1})}\mathbf{d}_{\mathbb{S}^{d-1}}(\boldsymbol{\upsilon}_{j_1},\boldsymbol{\upsilon}_{j_2})).} \end{align} $$
$$ \begin{align} {R_N^2(f)=\frac{1}{N}\sum_{\substack{j_1,j_2=1\\ j_1\neq j_2}}^N f(\boldsymbol{\upsilon}_{j_1},\boldsymbol{\upsilon}_{j_2}, c_d N^{{1}/({d-1})}\mathbf{d}_{\mathbb{S}^{d-1}}(\boldsymbol{\upsilon}_{j_1},\boldsymbol{\upsilon}_{j_2})).} \end{align} $$
Corollary 2.4. Let
![]() $d\geq 2$
,
$d\geq 2$
,
![]() $0\leq c<1$
and
$0\leq c<1$
and
![]() $\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
; furthermore, if
$\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
; furthermore, if
![]() $d=2$
, assume that
$d=2$
, assume that
![]() $\boldsymbol {\xi }$
is
$\boldsymbol {\xi }$
is
![]() $(0,0,2)$
-vaguely Diophantine. Then for any
$(0,0,2)$
-vaguely Diophantine. Then for any
![]() $f\in \operatorname {C}_0(\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}\times \mathbb {R})$
,
$f\in \operatorname {C}_0(\mathbb {S}^{d-1}\times \mathbb {S}^{d-1}\times \mathbb {R})$
,
 $$ \begin{align} {\lim_{T\to\infty}R_{N_c(T)}^2(f)= \frac{V_{\mathbb{S}^{d-2}}}{V_{\mathbb{S}^{d-1}}} \int_{\mathbb{S}^{d-1}\times\mathbb{R}_{\geq 0}}f(\boldsymbol{\upsilon},\boldsymbol{\upsilon},s)\, d\boldsymbol{\upsilon} \, s^{d-2}\,ds .} \end{align} $$
$$ \begin{align} {\lim_{T\to\infty}R_{N_c(T)}^2(f)= \frac{V_{\mathbb{S}^{d-2}}}{V_{\mathbb{S}^{d-1}}} \int_{\mathbb{S}^{d-1}\times\mathbb{R}_{\geq 0}}f(\boldsymbol{\upsilon},\boldsymbol{\upsilon},s)\, d\boldsymbol{\upsilon} \, s^{d-2}\,ds .} \end{align} $$
Corollary 2.4 implies Theorem 1.1 by approximating the characteristic function from above/below by
![]() $\operatorname {C}_0$
functions. The additional dependence of
$\operatorname {C}_0$
functions. The additional dependence of
![]() $f(\boldsymbol {\upsilon }_1,\boldsymbol {\upsilon }_2,s)$
on
$f(\boldsymbol {\upsilon }_1,\boldsymbol {\upsilon }_2,s)$
on
![]() ${\boldsymbol {\upsilon }_1,\boldsymbol {\upsilon }_2\in \mathbb {S}^{d-1}}$
can be used to generalize Theorem 1.1 to pair counting where
${\boldsymbol {\upsilon }_1,\boldsymbol {\upsilon }_2\in \mathbb {S}^{d-1}}$
can be used to generalize Theorem 1.1 to pair counting where
![]() $\boldsymbol {\upsilon }_{j_1}$
and
$\boldsymbol {\upsilon }_{j_1}$
and
![]() $\boldsymbol {\upsilon }_{j_2}$
are restricted to different subsets of
$\boldsymbol {\upsilon }_{j_2}$
are restricted to different subsets of
![]() $\mathcal {D}_1,\mathcal {D}_2\subseteq \mathbb {S}^{d-1}$
. Set
$\mathcal {D}_1,\mathcal {D}_2\subseteq \mathbb {S}^{d-1}$
. Set
 $$ \begin{align*} R^2_N(\mathcal{D}_1,\mathcal{D}_2,s) = \frac{1}{N} \#\{ &(j_1,j_2) : j_1,j_2\leq N, \, j_1\neq j_2, \\ &\boldsymbol{\upsilon}_{j_1}\in\mathcal{D}_1,\boldsymbol{\upsilon}_{j_2}\in\mathcal{D}_2,\,\, c_d N^{{1}/({d-1})}\mathbf{d}_{\mathbb{S}^{d-1}}(\boldsymbol{\upsilon}_{j_1},\boldsymbol{\upsilon}_{j_2}) \leq s \}. \end{align*} $$
$$ \begin{align*} R^2_N(\mathcal{D}_1,\mathcal{D}_2,s) = \frac{1}{N} \#\{ &(j_1,j_2) : j_1,j_2\leq N, \, j_1\neq j_2, \\ &\boldsymbol{\upsilon}_{j_1}\in\mathcal{D}_1,\boldsymbol{\upsilon}_{j_2}\in\mathcal{D}_2,\,\, c_d N^{{1}/({d-1})}\mathbf{d}_{\mathbb{S}^{d-1}}(\boldsymbol{\upsilon}_{j_1},\boldsymbol{\upsilon}_{j_2}) \leq s \}. \end{align*} $$
We then have the following corollary.
Corollary 2.5. Let
![]() $d\geq 2$
,
$d\geq 2$
,
![]() $0\leq c<1$
and
$0\leq c<1$
and
![]() $\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
; furthermore, if
$\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
; furthermore, if
![]() $d=2$
, assume that
$d=2$
, assume that
![]() $\boldsymbol {\xi }$
is
$\boldsymbol {\xi }$
is
![]() $(0,0,2)$
-vaguely Diophantine. Then for any
$(0,0,2)$
-vaguely Diophantine. Then for any
![]() $\mathcal {D}_1,\mathcal {D}_2\subseteq \mathbb {S}^{d-1}$
with
$\mathcal {D}_1,\mathcal {D}_2\subseteq \mathbb {S}^{d-1}$
with
![]() $\operatorname {vol}_{\mathbb {S}^{d-1}}(\partial \mathcal {D}_1)=\operatorname {vol}_{\mathbb {S}^{d-1}}(\partial \mathcal {D}_2)=0$
and
$\operatorname {vol}_{\mathbb {S}^{d-1}}(\partial \mathcal {D}_1)=\operatorname {vol}_{\mathbb {S}^{d-1}}(\partial \mathcal {D}_2)=0$
and
![]() $s>0$
, we have that
$s>0$
, we have that
 $$ \begin{align} {\lim_{T\to\infty}R_{N_c(T)}^2(\mathcal{D}_1,\mathcal{D}_2,s)= \frac{\pi^{({d-1})/{2}} s^{d-1}}{\Gamma(({d+1})/{2})} \;\frac{\operatorname{vol}_{\mathbb{S}^{d-1}}(\mathcal{D}_1\cap\mathcal{D}_2)}{V_{\mathbb{S}^{d-1}}}.} \end{align} $$
$$ \begin{align} {\lim_{T\to\infty}R_{N_c(T)}^2(\mathcal{D}_1,\mathcal{D}_2,s)= \frac{\pi^{({d-1})/{2}} s^{d-1}}{\Gamma(({d+1})/{2})} \;\frac{\operatorname{vol}_{\mathbb{S}^{d-1}}(\mathcal{D}_1\cap\mathcal{D}_2)}{V_{\mathbb{S}^{d-1}}}.} \end{align} $$
3. The space of affine lattices
Let
![]() $G=\operatorname {SL}(d,\mathbb {R})$
and
$G=\operatorname {SL}(d,\mathbb {R})$
and
![]() $\Gamma =\operatorname {SL}(d,\mathbb {Z})$
. Define
$\Gamma =\operatorname {SL}(d,\mathbb {Z})$
. Define
![]() $G'=G\ltimes \mathbb {R}^d$
by
$G'=G\ltimes \mathbb {R}^d$
by
and let
![]() $\Gamma '=\Gamma \ltimes \mathbb {Z}^d$
denote the corresponding arithmetic subgroup. The right action of
$\Gamma '=\Gamma \ltimes \mathbb {Z}^d$
denote the corresponding arithmetic subgroup. The right action of
![]() $g=(M,\mathbf {b})\in G'$
on
$g=(M,\mathbf {b})\in G'$
on
![]() $\mathbb {R}^d$
is defined by
$\mathbb {R}^d$
is defined by
![]() $\mathbf {x} g:=\mathbf {x} M +\mathbf {b}$
. We embed G in
$\mathbf {x} g:=\mathbf {x} M +\mathbf {b}$
. We embed G in
![]() $G'$
via the homomorphism
$G'$
via the homomorphism
![]() $M\mapsto (M,0)$
. In the following, we will identify G with the corresponding subgroup in
$M\mapsto (M,0)$
. In the following, we will identify G with the corresponding subgroup in
![]() $G'$
and use the shorthand M for
$G'$
and use the shorthand M for
![]() $(M,0)$
.
$(M,0)$
.
Given
![]() $\sigma>0$
and
$\sigma>0$
and
![]() $0\leq c<1$
, define the cone
$0\leq c<1$
, define the cone
For
![]() $g\in G'$
and any bounded set
$g\in G'$
and any bounded set
![]() $\mathfrak {C}\subset \mathbb {R}^d,$
$\mathfrak {C}\subset \mathbb {R}^d,$
By construction, we can view
![]() $\mathcal {N}(\cdot ,\mathfrak {C})$
as a function on the space of affine lattices,
$\mathcal {N}(\cdot ,\mathfrak {C})$
as a function on the space of affine lattices,
![]() $\Gamma '\backslash G'$
. For
$\Gamma '\backslash G'$
. For
![]() $\mathbf {y}=(y_2,\ldots ,y_{d})\in \mathbb {R}^{d-1}$
and
$\mathbf {y}=(y_2,\ldots ,y_{d})\in \mathbb {R}^{d-1}$
and
![]() $t\ge 0$
, let
$t\ge 0$
, let
 $$ \begin{align} {\widetilde{n}(\mathbf{y}):=\left(\begin{matrix} 1 & y_2 & \cdots & y_{d}\\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{matrix}\right)\!,\quad \Phi_t:=\left(\begin{matrix} e^{-(({d-1})/{d})t} & & & \\ & e^{{t}/{d}} & & \\ & & \ddots & \\ & & & e^{{t}/{d}} \end{matrix}\right)\!.} \end{align} $$
$$ \begin{align} {\widetilde{n}(\mathbf{y}):=\left(\begin{matrix} 1 & y_2 & \cdots & y_{d}\\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{matrix}\right)\!,\quad \Phi_t:=\left(\begin{matrix} e^{-(({d-1})/{d})t} & & & \\ & e^{{t}/{d}} & & \\ & & \ddots & \\ & & & e^{{t}/{d}} \end{matrix}\right)\!.} \end{align} $$
Set
![]() $\mathbf {e}_1=(1,0,\ldots ,0)$
. As in [Reference Marklof and StrömbergssonMS10, p. 1968], we define a smooth map
$\mathbf {e}_1=(1,0,\ldots ,0)$
. As in [Reference Marklof and StrömbergssonMS10, p. 1968], we define a smooth map
![]() $k:\mathbb {S}^{d-1}\setminus \{-\mathbf {e}_1\}\to \operatorname {SO}(d)$
by
$k:\mathbb {S}^{d-1}\setminus \{-\mathbf {e}_1\}\to \operatorname {SO}(d)$
by

with
![]() $\mathbf {y}(\mathbf {e}_1)=0$
and, for
$\mathbf {y}(\mathbf {e}_1)=0$
and, for
![]() $\boldsymbol {\upsilon }=(\upsilon _1,\ldots ,\upsilon _d)\in \mathbb {S}^{d-1}\setminus \{\mathbf {e}_1,-\mathbf {e}_1\}$
,
$\boldsymbol {\upsilon }=(\upsilon _1,\ldots ,\upsilon _d)\in \mathbb {S}^{d-1}\setminus \{\mathbf {e}_1,-\mathbf {e}_1\}$
,
 $$ \begin{align*}\mathbf{y}(\boldsymbol{\upsilon})=\frac{\operatorname{arc\cos} v_1}{\sqrt{1-\upsilon_1^2}}(\upsilon_2,\ldots,\upsilon_d)\in\mathbb{R}^{d-1}.\end{align*} $$
$$ \begin{align*}\mathbf{y}(\boldsymbol{\upsilon})=\frac{\operatorname{arc\cos} v_1}{\sqrt{1-\upsilon_1^2}}(\upsilon_2,\ldots,\upsilon_d)\in\mathbb{R}^{d-1}.\end{align*} $$
Note that
![]() $\|\mathbf {y}(\boldsymbol {\upsilon })\|<\pi $
. By construction,
$\|\mathbf {y}(\boldsymbol {\upsilon })\|<\pi $
. By construction,
![]() $\boldsymbol {\upsilon }=(\cos \|\mathbf {y}(\boldsymbol {\upsilon })\|,\sin \|\mathbf {y}(\boldsymbol {\upsilon })\|({\mathbf {y}(\boldsymbol {\upsilon })}/{\|\mathbf {y}(\boldsymbol {\upsilon })\|}))$
, and hence
$\boldsymbol {\upsilon }=(\cos \|\mathbf {y}(\boldsymbol {\upsilon })\|,\sin \|\mathbf {y}(\boldsymbol {\upsilon })\|({\mathbf {y}(\boldsymbol {\upsilon })}/{\|\mathbf {y}(\boldsymbol {\upsilon })\|}))$
, and hence
![]() $\mathbf {e}_1 =\boldsymbol {\upsilon } k(\boldsymbol {\upsilon })$
for all
$\mathbf {e}_1 =\boldsymbol {\upsilon } k(\boldsymbol {\upsilon })$
for all
![]() $\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}\setminus \{-\mathbf {e}_1\}$
.
$\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}\setminus \{-\mathbf {e}_1\}$
.
By an elementary geometric argument, given
![]() $\sigma>0$
and
$\sigma>0$
and
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $T_0>0$
such that for all
$T_0>0$
such that for all
![]() $\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}\setminus \{-\mathbf {e}_1\}$
,
$\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}\setminus \{-\mathbf {e}_1\}$
,
![]() $\boldsymbol {\xi }\in \mathbb {R}^d$
,
$\boldsymbol {\xi }\in \mathbb {R}^d$
,
![]() $M_0\in G$
and
$M_0\in G$
and
![]() $T=e^{{t}/{d}}\ge T_0$
,
$T=e^{{t}/{d}}\ge T_0$
,
The argument is the same as in the two-dimensional case discussed in [Reference El-Baz, Marklof and VinogradovEMV15]; see in particular Fig. 3 (the yellow and red domains should now be viewed as higher-dimensional cones with symmetry axis along
![]() $\mathbf {e}_1$
).
$\mathbf {e}_1$
).
For
and
let
 $$ \begin{align} {n(\mathbf{u}):=\left(\begin{matrix} 1 & u_{12} & \cdots & u_{1d}\\ & \ddots & & \vdots \\ & & 1 & u_{(d-1)d} \\ & & & 1 \end{matrix}\right)\!,\quad a(\mathbf{v}):=\left(\begin{matrix} v_1 & & & \\ & v_2 & & \\ & & \ddots & \\ & & & v_d \end{matrix}\right)\!.} \end{align} $$
$$ \begin{align} {n(\mathbf{u}):=\left(\begin{matrix} 1 & u_{12} & \cdots & u_{1d}\\ & \ddots & & \vdots \\ & & 1 & u_{(d-1)d} \\ & & & 1 \end{matrix}\right)\!,\quad a(\mathbf{v}):=\left(\begin{matrix} v_1 & & & \\ & v_2 & & \\ & & \ddots & \\ & & & v_d \end{matrix}\right)\!.} \end{align} $$
The Iwasawa decomposition of
![]() $M\in G$
is given by
$M\in G$
is given by
where
![]() $\mathbf {u}\in \mathbb {R}^{{d(d-1)}/{2}}$
,
$\mathbf {u}\in \mathbb {R}^{{d(d-1)}/{2}}$
,
![]() $\mathbf {v}\in \mathcal {T}$
and
$\mathbf {v}\in \mathcal {T}$
and
![]() $k\in \operatorname {SO}(d)$
.
$k\in \operatorname {SO}(d)$
.
Consider the Siegel set
 $$ \begin{align} {\mathcal{S}:=\bigg\{n(\mathbf{u})a(\mathbf{v})k: k\in \operatorname{SO}(d), 0<v_{j+1}\leq\frac{2}{\sqrt{3}}v_{j} ,\, \mathbf{u}\in\bigg[-\frac{1}{2},\frac{1}{2}\bigg]^{{d(d-1)}/{2}}\bigg\}.} \end{align} $$
$$ \begin{align} {\mathcal{S}:=\bigg\{n(\mathbf{u})a(\mathbf{v})k: k\in \operatorname{SO}(d), 0<v_{j+1}\leq\frac{2}{\sqrt{3}}v_{j} ,\, \mathbf{u}\in\bigg[-\frac{1}{2},\frac{1}{2}\bigg]^{{d(d-1)}/{2}}\bigg\}.} \end{align} $$
This set has the property that it contains a fundamental domain of G and can be covered with a finite number of fundamental domains. Throughout this paper, we fix a fundamental domain of G contained in
![]() $\mathcal {S}$
and denote it by
$\mathcal {S}$
and denote it by
![]() $\mathcal {F}$
. For
$\mathcal {F}$
. For
![]() $x\in \Gamma \backslash G$
, there exists a unique
$x\in \Gamma \backslash G$
, there exists a unique
![]() $M\in \mathcal {F}$
such that
$M\in \mathcal {F}$
such that
![]() $x=\Gamma M$
. Define
$x=\Gamma M$
. Define
![]() $\iota :\Gamma \backslash G\to \mathcal {F}$
so that
$\iota :\Gamma \backslash G\to \mathcal {F}$
so that
![]() $\iota (\Gamma M)=M$
.
$\iota (\Gamma M)=M$
.
We extend the above to define a fundamental domain
![]() $\mathcal {F}'$
and Siegel set
$\mathcal {F}'$
and Siegel set
![]() $\mathcal {S}'$
of the
$\mathcal {S}'$
of the
![]() $\Gamma '$
action on
$\Gamma '$
action on
![]() $G'$
by
$G'$
by
As before, we define the map
![]() $\iota :\Gamma '\backslash G'\to \mathcal {F}'$
by
$\iota :\Gamma '\backslash G'\to \mathcal {F}'$
by
![]() $\iota (\Gamma ' g)=g$
.
$\iota (\Gamma ' g)=g$
.
Given
![]() $M\in G$
, we define
$M\in G$
, we define
![]() $\mathbf {v}(M)$
as the
$\mathbf {v}(M)$
as the
![]() $\mathbf {v}$
coordinate of the Iwasawa decomposition
$\mathbf {v}$
coordinate of the Iwasawa decomposition
Similarly, for
![]() $g\in G'$
, we define
$g\in G'$
, we define
![]() $\mathbf {v}(g)$
and
$\mathbf {v}(g)$
and
![]() $\mathbf {b}(g)$
as the
$\mathbf {b}(g)$
as the
![]() $\mathbf {v}$
and
$\mathbf {v}$
and
![]() $\mathbf {b}$
coordinates in
$\mathbf {b}$
coordinates in
We also define
and
where
![]() $c_d=d({2}/{\sqrt {3}})^d$
.
$c_d=d({2}/{\sqrt {3}})^d$
.
Lemma 3.1. For any bounded
![]() $\mathfrak {C}\subset \mathbb {R}^d$
,
$\mathfrak {C}\subset \mathbb {R}^d$
,
![]() $g\in G'$
,
$g\in G'$
,
![]() $\eta>0$
,
$\eta>0$
,
 $$ \begin{align} {\mathcal{N}(g,\mathfrak{C})^\eta\leq (C_dr^d)^\eta\prod_{i=1}^{s}(v_i^\eta\#([-c_drv_i^{-1},c_drv_i^{-1}]\cap(\mathbb{Z}+b_i))),} \end{align} $$
$$ \begin{align} {\mathcal{N}(g,\mathfrak{C})^\eta\leq (C_dr^d)^\eta\prod_{i=1}^{s}(v_i^\eta\#([-c_drv_i^{-1},c_drv_i^{-1}]\cap(\mathbb{Z}+b_i))),} \end{align} $$
where
![]() $\mathbf {v}=\mathbf {v}(g)=(v_1,\ldots ,v_d)$
,
$\mathbf {v}=\mathbf {v}(g)=(v_1,\ldots ,v_d)$
,
![]() $\mathbf {b}=\mathbf {b}(g)=(b_1,\ldots ,b_d)$
,
$\mathbf {b}=\mathbf {b}(g)=(b_1,\ldots ,b_d)$
,
![]() $r=r(\mathfrak {C})$
,
$r=r(\mathfrak {C})$
,
![]() $s=s_r(g)$
and
$s=s_r(g)$
and
![]() $C_d=4c_d$
.
$C_d=4c_d$
.
Proof. Let
![]() $\mathfrak {D}_r$
be the smallest closed ball of radius r centred at
$\mathfrak {D}_r$
be the smallest closed ball of radius r centred at
![]() $0$
which contains
$0$
which contains
![]() $\mathfrak {C}$
. Then
$\mathfrak {C}$
. Then
 $$ \begin{align} \mathcal{N}(g,\mathfrak{C})&\leq\mathcal{N}(g,\mathfrak{D}_r)=\mathcal{N}(\iota(\Gamma g),\mathfrak{D}_r)\nonumber\\ &=\#(\mathfrak{D}_r\cap (\mathbb{Z}^d+\mathbf{b})n(\mathbf{u})a(\mathbf{v}))\nonumber\\ &\leq \#([-r,r]^d\cap(\mathbb{Z}^d+\mathbf{b})n(\mathbf{u})a(\mathbf{v}))\nonumber\\ &= \#\bigg(\prod_{i=1}^{d}[-rv_i^{-1},rv_i^{-1}]\cap(\mathbb{Z}^d+\mathbf{b})n(\mathbf{u})\bigg). \end{align} $$
$$ \begin{align} \mathcal{N}(g,\mathfrak{C})&\leq\mathcal{N}(g,\mathfrak{D}_r)=\mathcal{N}(\iota(\Gamma g),\mathfrak{D}_r)\nonumber\\ &=\#(\mathfrak{D}_r\cap (\mathbb{Z}^d+\mathbf{b})n(\mathbf{u})a(\mathbf{v}))\nonumber\\ &\leq \#([-r,r]^d\cap(\mathbb{Z}^d+\mathbf{b})n(\mathbf{u})a(\mathbf{v}))\nonumber\\ &= \#\bigg(\prod_{i=1}^{d}[-rv_i^{-1},rv_i^{-1}]\cap(\mathbb{Z}^d+\mathbf{b})n(\mathbf{u})\bigg). \end{align} $$
Since
![]() $0<v_{i+1}\leq ({2}/{\sqrt {3}})v_i$
for
$0<v_{i+1}\leq ({2}/{\sqrt {3}})v_i$
for
![]() $1\leq i\leq d-1$
, we have
$1\leq i\leq d-1$
, we have
![]() $v_j^{-1}\leq ({2}/{\sqrt {3}})^{j-i}v_i^{-1}$
for any
$v_j^{-1}\leq ({2}/{\sqrt {3}})^{j-i}v_i^{-1}$
for any
![]() ${1\leq i< j\leq d}$
. It follows that
${1\leq i< j\leq d}$
. It follows that
 $$ \begin{align} \mathcal{N}(g,\mathfrak{C})&\leq \#\bigg(\prod_{i=1}^{d}[-c_drv_i^{-1},c_drv_i^{-1}]\cap(\mathbb{Z}^d+\mathbf{b})\bigg)\nonumber\\ &\leq\prod_{i=1}^{d}\#([-c_drv_i^{-1},c_drv_i^{-1}]\cap(\mathbb{Z}+b_i))\nonumber\\ &\leq\prod_{i=s+1}^{d}(2c_drv_i^{-1}+1)\times\prod_{i=1}^{s}\#([-c_drv_i^{-1},c_drv_i^{-1}]\cap(\mathbb{Z}+b_i)). \end{align} $$
$$ \begin{align} \mathcal{N}(g,\mathfrak{C})&\leq \#\bigg(\prod_{i=1}^{d}[-c_drv_i^{-1},c_drv_i^{-1}]\cap(\mathbb{Z}^d+\mathbf{b})\bigg)\nonumber\\ &\leq\prod_{i=1}^{d}\#([-c_drv_i^{-1},c_drv_i^{-1}]\cap(\mathbb{Z}+b_i))\nonumber\\ &\leq\prod_{i=s+1}^{d}(2c_drv_i^{-1}+1)\times\prod_{i=1}^{s}\#([-c_drv_i^{-1},c_drv_i^{-1}]\cap(\mathbb{Z}+b_i)). \end{align} $$
For
![]() $i\ge s+1$
, we have
$i\ge s+1$
, we have
![]() $v_i^{-1}\ge {1}/{2c_dr}$
by definition of s. It follows that
$v_i^{-1}\ge {1}/{2c_dr}$
by definition of s. It follows that
 $$ \begin{align*}\prod_{i=s+1}^{d}(2c_drv_i^{-1}+1)\leq (4c_dr)^{d-s}\prod_{i=s+1}^{d}v_i^{-1}=(4c_dr)^{d-s}\prod_{i=1}^{s}v_i,\end{align*} $$
$$ \begin{align*}\prod_{i=s+1}^{d}(2c_drv_i^{-1}+1)\leq (4c_dr)^{d-s}\prod_{i=s+1}^{d}v_i^{-1}=(4c_dr)^{d-s}\prod_{i=1}^{s}v_i,\end{align*} $$
and hence
 $$ \begin{align*}\mathcal{N}(g,\mathfrak{C})\leq C_dr^d\prod_{i=1}^{s}(v_i\#([-c_drv_i^{-1},c_drv_i^{-1}]\cap(\mathbb{Z}+b_i))).\end{align*} $$
$$ \begin{align*}\mathcal{N}(g,\mathfrak{C})\leq C_dr^d\prod_{i=1}^{s}(v_i\#([-c_drv_i^{-1},c_drv_i^{-1}]\cap(\mathbb{Z}+b_i))).\end{align*} $$
From the fact that
for any
![]() $1\leq i\leq s$
, equation (3.13) follows.
$1\leq i\leq s$
, equation (3.13) follows.
The case of mixed moment will be dealt with by the inequality
4. Properties of the limiting distribution
In this section, we prove the properties (a)–(e) of the limiting distribution in Theorem 2.1. We denote by
![]() $m_{X'}$
,
$m_{X'}$
,
![]() $m_{X_1}$
and
$m_{X_1}$
and
![]() $m_{X_q}$
the Haar probability measures on the homogeneous spaces
$m_{X_q}$
the Haar probability measures on the homogeneous spaces
respectively. Here,
![]() $\Gamma _q$
denotes the congruence subgroup
$\Gamma _q$
denotes the congruence subgroup
for
![]() $q\ge 2$
. According to [Reference Marklof and StrömbergssonMS10, Theorems 6.3, 6.5 and subsequent remarks, and Lemma 9.5], the limiting distribution
$q\ge 2$
. According to [Reference Marklof and StrömbergssonMS10, Theorems 6.3, 6.5 and subsequent remarks, and Lemma 9.5], the limiting distribution
![]() $E_{c,\boldsymbol {\xi }}(\cdot ,\underline {\sigma })$
in Theorem 2.1 is given as follows:
$E_{c,\boldsymbol {\xi }}(\cdot ,\underline {\sigma })$
in Theorem 2.1 is given as follows:
 $$ \begin{align} E_{c,\boldsymbol{\xi}}(\underline{r},\underline{\sigma}) = \begin{cases} & \kern-10pt m_{X_1}(\{\Gamma M\in X_1: \text{for all } j, \; \#(\mathbb{Z}^dM\cap \mathfrak{C}_c(\sigma_j))=r_j\})\\& \qquad\qquad\qquad\qquad\qquad\qquad \text{if}\ \boldsymbol{\xi}\in\mathbb{Z}^d,\\& \kern-10pt m_{X_q}\bigg(\bigg\{\Gamma_q M\in X_q: \text{for all } j, \; \#\bigg(\bigg(\mathbb{Z}^d+\dfrac{\mathbf{p}}{q}\bigg)M\cap \mathfrak{C}_c(\sigma_j)\bigg)=r_j \bigg\}\bigg)\\& \qquad\qquad\qquad\qquad\qquad\qquad \text{if}\ \boldsymbol{\xi}=\dfrac{\mathbf{p}}{q}\in\mathbb{Q}^d\setminus \mathbb{Z}^d,\\& \kern-10pt m_{X_q}(\{\Gamma'g\in X': \text{for all } j, \; \#(\mathbb{Z}^d g\cap \mathfrak{C}_c(\sigma_j))=r_j \})\\& \qquad\qquad\qquad\qquad\qquad\qquad \text{if}\ \boldsymbol{\xi}\in\mathbb{R}^d\setminus \mathbb{Q}^d, \end{cases} \end{align} $$
$$ \begin{align} E_{c,\boldsymbol{\xi}}(\underline{r},\underline{\sigma}) = \begin{cases} & \kern-10pt m_{X_1}(\{\Gamma M\in X_1: \text{for all } j, \; \#(\mathbb{Z}^dM\cap \mathfrak{C}_c(\sigma_j))=r_j\})\\& \qquad\qquad\qquad\qquad\qquad\qquad \text{if}\ \boldsymbol{\xi}\in\mathbb{Z}^d,\\& \kern-10pt m_{X_q}\bigg(\bigg\{\Gamma_q M\in X_q: \text{for all } j, \; \#\bigg(\bigg(\mathbb{Z}^d+\dfrac{\mathbf{p}}{q}\bigg)M\cap \mathfrak{C}_c(\sigma_j)\bigg)=r_j \bigg\}\bigg)\\& \qquad\qquad\qquad\qquad\qquad\qquad \text{if}\ \boldsymbol{\xi}=\dfrac{\mathbf{p}}{q}\in\mathbb{Q}^d\setminus \mathbb{Z}^d,\\& \kern-10pt m_{X_q}(\{\Gamma'g\in X': \text{for all } j, \; \#(\mathbb{Z}^d g\cap \mathfrak{C}_c(\sigma_j))=r_j \})\\& \qquad\qquad\qquad\qquad\qquad\qquad \text{if}\ \boldsymbol{\xi}\in\mathbb{R}^d\setminus \mathbb{Q}^d, \end{cases} \end{align} $$
where
![]() $\mathfrak {C}_c(\sigma )$
is as in equation (3.1).
$\mathfrak {C}_c(\sigma )$
is as in equation (3.1).
Property (a) follows from the observation that the distribution described in equation (4.1) is independent of
![]() $\unicode{x3bb} $
and
$\unicode{x3bb} $
and
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
For
![]() $\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
, the distribution is also independent of
$\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
, the distribution is also independent of
![]() $\boldsymbol {\xi }$
, so property (d) follows.
$\boldsymbol {\xi }$
, so property (d) follows.
Property (b) follows from equation (2.1).
Properties (c) and (e) follow from calculations of [Reference MarklofM00]. We write
![]() ${g\kern1.3pt{=}\kern1.3pt(1,\mathbf {b})(M,0)\kern1.3pt{\in}\kern1.3pt G'}$
with
${g\kern1.3pt{=}\kern1.3pt(1,\mathbf {b})(M,0)\kern1.3pt{\in}\kern1.3pt G'}$
with
![]() $M=n(\mathbf {u})a(\mathbf {v})k\in \mathcal {S}$
as in equations (3.7) and (3.8). For
$M=n(\mathbf {u})a(\mathbf {v})k\in \mathcal {S}$
as in equations (3.7) and (3.8). For
![]() $s\in \{1,\ldots ,d-1\}$
, put
$s\in \{1,\ldots ,d-1\}$
, put
 $$ \begin{align*} {\mathcal{S}_s:=\bigg\{M=n(\mathbf{u})a(\mathbf{v})k\in\mathcal{S}: v_{s+1}\leq 1 \leq\frac{2}{\sqrt{3}}v_s\bigg\},} \end{align*} $$
$$ \begin{align*} {\mathcal{S}_s:=\bigg\{M=n(\mathbf{u})a(\mathbf{v})k\in\mathcal{S}: v_{s+1}\leq 1 \leq\frac{2}{\sqrt{3}}v_s\bigg\},} \end{align*} $$
and for
![]() $s=0,d,$
$s=0,d,$
 $$ \begin{align*} {\mathcal{S}_d:=\bigg\{M=n(\mathbf{u})a(\mathbf{v})k\in\mathcal{S}: v_d\geq \frac{\sqrt{3}}{2}\bigg\},} \end{align*} $$
$$ \begin{align*} {\mathcal{S}_d:=\bigg\{M=n(\mathbf{u})a(\mathbf{v})k\in\mathcal{S}: v_d\geq \frac{\sqrt{3}}{2}\bigg\},} \end{align*} $$
then the sets
![]() $\mathcal {S}_0$
and
$\mathcal {S}_0$
and
![]() $\mathcal {S}_d$
are clearly compact, and we also have
$\mathcal {S}_d$
are clearly compact, and we also have
![]() $\mathcal {S}=\bigcup _{s=0}^{d}\mathcal {S}_s$
(see [Reference MarklofM00, Lemma 3.12]). For
$\mathcal {S}=\bigcup _{s=0}^{d}\mathcal {S}_s$
(see [Reference MarklofM00, Lemma 3.12]). For
![]() $k\in \operatorname {SO}(d)$
, we denote by
$k\in \operatorname {SO}(d)$
, we denote by
![]() $\chi _k$
the characteristic function of the set
$\chi _k$
the characteristic function of the set
![]() $\mathfrak {C}_c(\sigma )k^{-1}$
and define
$\mathfrak {C}_c(\sigma )k^{-1}$
and define
We have
where
![]() $w_i(\mathbf {m})=(m_i+b_i)+\sum _{j=1}^{i-1}u_{ji}(m_j+b_j)$
. Without loss of generality, we may assume
$w_i(\mathbf {m})=(m_i+b_i)+\sum _{j=1}^{i-1}u_{ji}(m_j+b_j)$
. Without loss of generality, we may assume
![]() $b_1,\ldots ,b_d\in [-\tfrac 12,\tfrac 12]$
. For
$b_1,\ldots ,b_d\in [-\tfrac 12,\tfrac 12]$
. For
![]() $M\in \mathcal {S}_s$
with sufficiently large
$M\in \mathcal {S}_s$
with sufficiently large
![]() $v_1\cdots v_s$
,
$v_1\cdots v_s$
,
 $$ \begin{align*} {\begin{aligned}\mathcal{N}(g,\mathfrak{C}_c(\sigma))&=\sum_{\mathbf{m}\in \{\mathbf{0}\}\times\mathbb{Z}^{d-s}}\chi_k(v_1w_1(\mathbf{m}),\ldots,v_dw_d(\mathbf{m}))\\ &=v_{s+1}^{-1}\cdots v_{d}^{-1}\phi_s(k,v_1x_1,\ldots,v_sx_s)+O(1),\end{aligned}} \end{align*} $$
$$ \begin{align*} {\begin{aligned}\mathcal{N}(g,\mathfrak{C}_c(\sigma))&=\sum_{\mathbf{m}\in \{\mathbf{0}\}\times\mathbb{Z}^{d-s}}\chi_k(v_1w_1(\mathbf{m}),\ldots,v_dw_d(\mathbf{m}))\\ &=v_{s+1}^{-1}\cdots v_{d}^{-1}\phi_s(k,v_1x_1,\ldots,v_sx_s)+O(1),\end{aligned}} \end{align*} $$
where
![]() $x_i=b_i+\sum _{j=1}^{i-1}u_{ji}b_j$
for
$x_i=b_i+\sum _{j=1}^{i-1}u_{ji}b_j$
for
![]() $i=1,\ldots ,s$
.
$i=1,\ldots ,s$
.
We first consider the case of
![]() $E_{c,\boldsymbol {\xi }}$
for
$E_{c,\boldsymbol {\xi }}$
for
![]() $\boldsymbol {\xi }\in \mathbb {Z}^d$
. For
$\boldsymbol {\xi }\in \mathbb {Z}^d$
. For
![]() $r_0\to \infty $
and
$r_0\to \infty $
and
![]() $m_G$
denoting the Haar measure of G (with arbitrary normalization),
$m_G$
denoting the Haar measure of G (with arbitrary normalization),
 $$ \begin{align*} {\begin{aligned} \sum_{r=r_0}^{\infty}E_{c,\boldsymbol{\xi}}(r,\sigma)&=m_{X_1}(\{M\in X_1: \mathcal{N}(g,\mathfrak{C}_c(\sigma))\ge r_0\}) \\&\asymp\sum_{s=0}^{d}m_G(\{M\in\mathcal{S}_s: v_1\cdots v_s\phi_s(k,0,\ldots,0)\ge r_0+O(1)\}) \\&\asymp\sum_{s=0}^{d}m_G\bigg(\bigg\{M\in\mathcal{S}_s: v_1\cdots v_s\ge \frac{r_0+O(1)}{\phi_{s,\operatorname\max}(0,\ldots,0)}\bigg\}\bigg). \end{aligned}} \end{align*} $$
$$ \begin{align*} {\begin{aligned} \sum_{r=r_0}^{\infty}E_{c,\boldsymbol{\xi}}(r,\sigma)&=m_{X_1}(\{M\in X_1: \mathcal{N}(g,\mathfrak{C}_c(\sigma))\ge r_0\}) \\&\asymp\sum_{s=0}^{d}m_G(\{M\in\mathcal{S}_s: v_1\cdots v_s\phi_s(k,0,\ldots,0)\ge r_0+O(1)\}) \\&\asymp\sum_{s=0}^{d}m_G\bigg(\bigg\{M\in\mathcal{S}_s: v_1\cdots v_s\ge \frac{r_0+O(1)}{\phi_{s,\operatorname\max}(0,\ldots,0)}\bigg\}\bigg). \end{aligned}} \end{align*} $$
In the last line, we are using the continuity of
![]() $\phi _{s,\operatorname \max }$
with respect to
$\phi _{s,\operatorname \max }$
with respect to
![]() $k\in \operatorname {SO}(d)$
. According to the calculation of [Reference MarklofM00, Proof of Theorem 3.11] with
$k\in \operatorname {SO}(d)$
. According to the calculation of [Reference MarklofM00, Proof of Theorem 3.11] with
![]() $n=2$
, the sum in the last line is
$n=2$
, the sum in the last line is
![]() $\asymp r_0^{-d}$
. This proves property (c) for
$\asymp r_0^{-d}$
. This proves property (c) for
![]() $\boldsymbol {\xi }\in \mathbb {Z}^d$
. The case of other
$\boldsymbol {\xi }\in \mathbb {Z}^d$
. The case of other
![]() $\boldsymbol {\xi }\in \mathbb {Q}^d$
is analogous.
$\boldsymbol {\xi }\in \mathbb {Q}^d$
is analogous.
In the case of
![]() $\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
, we get
$\boldsymbol {\xi }\in \mathbb {R}^d\setminus \mathbb {Q}^d$
, we get
 $$ \begin{align*} {\begin{aligned} \sum_{r=r_0}^{\infty}E_{c,\boldsymbol{\xi}}(r,\sigma)&=m_{X'}(\{g\in X': \mathcal{N}(g,\mathfrak{C}_c(\sigma))\ge r_0\}) \\&\asymp\sum_{s=0}^{d}m_G(\{M\in\mathcal{S}_s: v_1\cdots v_s\phi_s(k,v_1x_1,\ldots,v_sx_s)\ge r_0+O(1)\}) \\&\asymp\sum_{s=0}^{d}m_G\bigg(\bigg\{M\in\mathcal{S}_s: v_1\cdots v_s\ge \frac{r_0+O(1)}{\phi_{s,\operatorname\max}(v_1x_1,\ldots,v_sx_s)}\bigg\}\bigg). \end{aligned}} \end{align*} $$
$$ \begin{align*} {\begin{aligned} \sum_{r=r_0}^{\infty}E_{c,\boldsymbol{\xi}}(r,\sigma)&=m_{X'}(\{g\in X': \mathcal{N}(g,\mathfrak{C}_c(\sigma))\ge r_0\}) \\&\asymp\sum_{s=0}^{d}m_G(\{M\in\mathcal{S}_s: v_1\cdots v_s\phi_s(k,v_1x_1,\ldots,v_sx_s)\ge r_0+O(1)\}) \\&\asymp\sum_{s=0}^{d}m_G\bigg(\bigg\{M\in\mathcal{S}_s: v_1\cdots v_s\ge \frac{r_0+O(1)}{\phi_{s,\operatorname\max}(v_1x_1,\ldots,v_sx_s)}\bigg\}\bigg). \end{aligned}} \end{align*} $$
In this case, we use the calculation of [Reference MarklofM00, Proof of Theorem 4.3] which implies that the sum in the last line is
![]() $\asymp r_0^{-d-1}$
. This proves property (e).
$\asymp r_0^{-d-1}$
. This proves property (e).
5. Escape of mass
Denote by
![]() $\chi _{I}$
the characteristic function of a subset
$\chi _{I}$
the characteristic function of a subset
![]() $I\subseteq \mathbb {R}$
. For
$I\subseteq \mathbb {R}$
. For
![]() $R\ge 1$
and
$R\ge 1$
and
![]() $\eta ,r>0$
, define the
$\eta ,r>0$
, define the
![]() $\Gamma '$
-invariant function
$\Gamma '$
-invariant function
![]() $F_{R,\eta ,r}:G'\to \mathbb {R}$
by
$F_{R,\eta ,r}:G'\to \mathbb {R}$
by
 $$ \begin{align} {\begin{aligned} F_{R,\eta,r}(g):=\chi_{[R,\infty)}\bigg(\prod_{i=1}^{s_r(g)}v_i(g)\bigg)\; \prod_{i=1}^{s_r(g)} v_i(g)^\eta \chi_{[-c_dr,c_dr]}(v_i(g) b_i(g)). \end{aligned}} \end{align} $$
$$ \begin{align} {\begin{aligned} F_{R,\eta,r}(g):=\chi_{[R,\infty)}\bigg(\prod_{i=1}^{s_r(g)}v_i(g)\bigg)\; \prod_{i=1}^{s_r(g)} v_i(g)^\eta \chi_{[-c_dr,c_dr]}(v_i(g) b_i(g)). \end{aligned}} \end{align} $$
In view of Lemma 3.1, and equations (3.16) and (3.17), we note that for
and all
![]() $g\in G$
such that
$g\in G$
such that
![]() $\prod _{i=1}^{s_r(g)}v_i(g)\ge R$
with R sufficiently large, we have that
$\prod _{i=1}^{s_r(g)}v_i(g)\ge R$
with R sufficiently large, we have that
The following proposition establishes under which conditions there is no escape of mass in the equidistribution of horospheres with respect to the function
![]() $F_{R,\eta ,r}$
and thus also for
$F_{R,\eta ,r}$
and thus also for
![]() $\mathcal {N}(g,\mathfrak {C}_1)^{z_1}\cdots \mathcal {N}(g,\mathfrak {C}_m)^{z_m}$
.
$\mathcal {N}(g,\mathfrak {C}_1)^{z_1}\cdots \mathcal {N}(g,\mathfrak {C}_m)^{z_m}$
.
Proposition 5.1. Let
![]() $\boldsymbol {\xi }\in \mathbb {R}^d$
,
$\boldsymbol {\xi }\in \mathbb {R}^d$
,
![]() $M_0\in G$
,
$M_0\in G$
,
![]() $\eta ,r>0$
and
$\eta ,r>0$
and
![]() $\psi \in \operatorname {C}_0(\mathbb {R}^{d-1})$
. Assume that one of the following hypotheses hold:
$\psi \in \operatorname {C}_0(\mathbb {R}^{d-1})$
. Assume that one of the following hypotheses hold:
-
(B1)
 $\eta <d$
;
$\eta <d$
; -
(B2)
 $\eta <d+1$
and
$\eta <d+1$
and
 $\boldsymbol {\xi }$
is
$\boldsymbol {\xi }$
is
 $(0,\eta -2,2)$
-vaguely Diophantine if
$(0,\eta -2,2)$
-vaguely Diophantine if
 $d=2$
and
$d=2$
and
 $(d-1, \eta -d,1)$
-vaguely Diophantine if
$(d-1, \eta -d,1)$
-vaguely Diophantine if
 $d\geq 3$
.
$d\geq 3$
.
Then
 $$ \begin{align} {\lim_{R\to\infty}\limsup_{t\to \infty}\bigg|\!\int_{\mathbf{y}\in\mathbb{R}^{d-1}}F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\psi(\mathbf{y})\,d\mathbf{y}\bigg|=0.} \end{align} $$
$$ \begin{align} {\lim_{R\to\infty}\limsup_{t\to \infty}\bigg|\!\int_{\mathbf{y}\in\mathbb{R}^{d-1}}F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\psi(\mathbf{y})\,d\mathbf{y}\bigg|=0.} \end{align} $$
To prepare for the proof of this statement, put
![]() $\mathcal {K}:=\mathrm {supp\,} \psi $
. Without loss of generality, we may assume
$\mathcal {K}:=\mathrm {supp\,} \psi $
. Without loss of generality, we may assume
![]() $\mathcal {K}\subset [-1,1]^{d-1}$
. Indeed, there exists
$\mathcal {K}\subset [-1,1]^{d-1}$
. Indeed, there exists
![]() $s_0\ge 0$
such that
$s_0\ge 0$
such that
![]() ${e^{-s_0}\mathcal {K}\subset [-1,1]^{d-1}}$
, so we may replace
${e^{-s_0}\mathcal {K}\subset [-1,1]^{d-1}}$
, so we may replace
![]() $M_0,\mathbf {y}$
and
$M_0,\mathbf {y}$
and
![]() $\Phi _t$
in equation (5.4) by
$\Phi _t$
in equation (5.4) by
![]() $M_0\Phi _{-s_0}, e^{s_0}\mathbf {y}$
and
$M_0\Phi _{-s_0}, e^{s_0}\mathbf {y}$
and
![]() $\Phi _{t+s_0}$
, respectively, and reduce it to the case
$\Phi _{t+s_0}$
, respectively, and reduce it to the case
![]() $\mathcal {K}\subset [-1,1]^{d-1}$
.
$\mathcal {K}\subset [-1,1]^{d-1}$
.
Next we define two maps
![]() $\gamma =\gamma _t:\mathbb {R}^{d-1}\to \Gamma $
and
$\gamma =\gamma _t:\mathbb {R}^{d-1}\to \Gamma $
and
![]() $h=h_t:\mathbb {R}^{d-1}\to \mathcal {F}$
as follows. For
$h=h_t:\mathbb {R}^{d-1}\to \mathcal {F}$
as follows. For
![]() $\mathbf {y}\in \mathbb {R}^{d-1}$
,
$\mathbf {y}\in \mathbb {R}^{d-1}$
,
![]() $t\in \mathbb {R}$
, there exist unique
$t\in \mathbb {R}$
, there exist unique
![]() $\gamma (\mathbf {y})=\gamma _t(\mathbf {y})\in \Gamma $
and
$\gamma (\mathbf {y})=\gamma _t(\mathbf {y})\in \Gamma $
and
![]() $h(\mathbf {y})=h_t(\mathbf {y})\in \mathcal {F}$
such that
$h(\mathbf {y})=h_t(\mathbf {y})\in \mathcal {F}$
such that
Note that
![]() $\Gamma '(1,\boldsymbol {\xi })M_0\widetilde {n}(\mathbf {y})\Phi _t$
in equation (5.4) can now be expressed as
$\Gamma '(1,\boldsymbol {\xi })M_0\widetilde {n}(\mathbf {y})\Phi _t$
in equation (5.4) can now be expressed as
For
![]() $1\leq s\leq d-1$
and
$1\leq s\leq d-1$
and
![]() $\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}^s_{\ge 0}$
, we let
$\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}^s_{\ge 0}$
, we let
with
![]() $\delta _d=d4^d$
. Then for
$\delta _d=d4^d$
. Then for
![]() $g=(1,\boldsymbol {\xi } \gamma (\mathbf {y}))h(\mathbf {y})$
with
$g=(1,\boldsymbol {\xi } \gamma (\mathbf {y}))h(\mathbf {y})$
with
![]() $h(\mathbf {y})\in \Xi _{\underline {l}}^s$
, we have
$h(\mathbf {y})\in \Xi _{\underline {l}}^s$
, we have
where
![]() $l=l_1+\cdots +l_s$
. It follows that the integral in equation (5.4) is bounded by
$l=l_1+\cdots +l_s$
. It follows that the integral in equation (5.4) is bounded by
 $$ \begin{align} &\bigg|\!\int_{\mathbf{y}\in\mathcal{K}}F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\,d\mathbf{y}\bigg|\nonumber\\ &\quad\ll\sum_{s=1}^{d-1}\sum_{l=\lfloor\log_2 R\rfloor}^{\infty} 2^{\eta l} \sum_{\substack{\underline{l}=(l_1,\ldots,l_s)\in\mathbb{Z}^s_{\ge0}, \\ l_1+\cdots+l_s=l}}\operatorname{vol}_{\mathbb{R}^{d-1}}(\{\mathbf{y}\in\mathcal{K}: h(\mathbf{y})\in\Xi_{\underline{l}}^s\} ). \end{align} $$
$$ \begin{align} &\bigg|\!\int_{\mathbf{y}\in\mathcal{K}}F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\,d\mathbf{y}\bigg|\nonumber\\ &\quad\ll\sum_{s=1}^{d-1}\sum_{l=\lfloor\log_2 R\rfloor}^{\infty} 2^{\eta l} \sum_{\substack{\underline{l}=(l_1,\ldots,l_s)\in\mathbb{Z}^s_{\ge0}, \\ l_1+\cdots+l_s=l}}\operatorname{vol}_{\mathbb{R}^{d-1}}(\{\mathbf{y}\in\mathcal{K}: h(\mathbf{y})\in\Xi_{\underline{l}}^s\} ). \end{align} $$
This will be sufficient for proving case (B1). For hypothesis (B2), we need a refinement that also considers the size of
![]() $\boldsymbol {\xi }\gamma (\mathbf {y})$
; see equation (5.23) below.
$\boldsymbol {\xi }\gamma (\mathbf {y})$
; see equation (5.23) below.
Let us write ![]() for
for
![]() $1\leq i\leq d$
and
$1\leq i\leq d$
and
![]() $\mathbf {y}\in \mathbb {R}^{d-1}$
, and consider the Iwasawa decomposition of
$\mathbf {y}\in \mathbb {R}^{d-1}$
, and consider the Iwasawa decomposition of
![]() $h(\mathbf {y})$
,
$h(\mathbf {y})$
,
Lemma 5.2. If
![]() $h(\mathbf {y})\in \Xi ^s_{\underline {l}}$
for
$h(\mathbf {y})\in \Xi ^s_{\underline {l}}$
for
![]() $\underline {l}\in \mathbb {Z}_{\ge 0}^{s}$
, then
$\underline {l}\in \mathbb {Z}_{\ge 0}^{s}$
, then
![]() $|\boldsymbol {\beta }_i(\mathbf {y})|< 2^{-l_i}$
for all
$|\boldsymbol {\beta }_i(\mathbf {y})|< 2^{-l_i}$
for all
![]() $1\leq i\leq s$
.
$1\leq i\leq s$
.
Proof. For the sake of simplicity, we write
![]() $v_{i}=v_{i}(h(\mathbf {y}))$
for
$v_{i}=v_{i}(h(\mathbf {y}))$
for
![]() $1\hspace{-0.5pt}\leq\hspace{-0.5pt} i\hspace{-0.5pt}\leq\hspace{-0.5pt} d$
and
$1\hspace{-0.5pt}\leq\hspace{-0.5pt} i\hspace{-0.5pt}\leq\hspace{-0.5pt} d$
and
![]() ${u_{ij}\hspace{-0.5pt}=\hspace{-0.5pt}u_{ij}(h(\mathbf {y}))}$
for
${u_{ij}\hspace{-0.5pt}=\hspace{-0.5pt}u_{ij}(h(\mathbf {y}))}$
for
![]() $1\leq i<j\leq d$
. We also define
$1\leq i<j\leq d$
. We also define
![]() $\widetilde {\mathbf {u}}(\mathbf {y})\hspace{-0.5pt}=\hspace{-0.5pt}(\widetilde {u}_{ij})_{1\leq i<j\leq d}$
by
$\widetilde {\mathbf {u}}(\mathbf {y})\hspace{-0.5pt}=\hspace{-0.5pt}(\widetilde {u}_{ij})_{1\leq i<j\leq d}$
by
![]() ${n(\widetilde {\mathbf {u}}(\mathbf {y}))=n(\mathbf {u}(\mathbf {y}))^{-1}}$
. Note that each
${n(\widetilde {\mathbf {u}}(\mathbf {y}))=n(\mathbf {u}(\mathbf {y}))^{-1}}$
. Note that each
![]() $\widetilde {u}_{ij}$
can be expressed in terms of at most
$\widetilde {u}_{ij}$
can be expressed in terms of at most
![]() $2^d$
monomials of
$2^d$
monomials of
![]() $u_{12},\ldots ,u_{(d-1)d}$
with coefficients
$u_{12},\ldots ,u_{(d-1)d}$
with coefficients
![]() $\pm 1$
, and hence
$\pm 1$
, and hence
![]() $|\widetilde {u}_{ij}|\leq 2^d$
for any
$|\widetilde {u}_{ij}|\leq 2^d$
for any
![]() $1\leq i<j\leq d$
.
$1\leq i<j\leq d$
.
If
![]() $h(\mathbf {y})\in \Xi ^s_{l}$
, then we have
$h(\mathbf {y})\in \Xi ^s_{l}$
, then we have

for
![]() $1\leq i\leq d$
. Since
$1\leq i\leq d$
. Since
![]() $v_{j}^{-1}\leq ({2}/{\sqrt {3}})^{i-j}v_{i}^{-1}\leq 2^dv_i^{-1}$
for any
$v_{j}^{-1}\leq ({2}/{\sqrt {3}})^{i-j}v_{i}^{-1}\leq 2^dv_i^{-1}$
for any
![]() $1\leq j<i\leq d$
,
$1\leq j<i\leq d$
,
 $$ \begin{align*} {|\boldsymbol{\beta}_i(\mathbf{y})|=\bigg|v_i^{-1}\mathbf{e}_i-\sum_{j=1}^{i-1}v_{j}^{-1}\widetilde{u}_{ji}\mathbf{e}_j\bigg|\leq d4^d v_i^{-1}=\delta_d v_i^{-1}< 2^{-l_i}} \end{align*} $$
$$ \begin{align*} {|\boldsymbol{\beta}_i(\mathbf{y})|=\bigg|v_i^{-1}\mathbf{e}_i-\sum_{j=1}^{i-1}v_{j}^{-1}\widetilde{u}_{ji}\mathbf{e}_j\bigg|\leq d4^d v_i^{-1}=\delta_d v_i^{-1}< 2^{-l_i}} \end{align*} $$
for all
![]() $1\leq i\leq s$
.
$1\leq i\leq s$
.
Denote by
![]() $\pi _1:\mathbb {R}^d\to \mathbb {R}$
and the orthogonal projection to the first coordinate and
$\pi _1:\mathbb {R}^d\to \mathbb {R}$
and the orthogonal projection to the first coordinate and
![]() $\pi ':\mathbb {R}^d\to \mathbb {R}^{d-1}$
the orthogonal projection to the remaining
$\pi ':\mathbb {R}^d\to \mathbb {R}^{d-1}$
the orthogonal projection to the remaining
![]() $(d-1)$
coordinates. Let
$(d-1)$
coordinates. Let ![]() and, for
and, for
![]() $k\in \mathbb {Z}$
, let
$k\in \mathbb {Z}$
, let
Then for sufficiently large k,
where the implied constants are independent of k but depend on the fixed
![]() $M_0\in G$
. Throughout this section, let
$M_0\in G$
. Throughout this section, let
![]() $K_0\in \mathbb {Z}$
be the largest integer such that
$K_0\in \mathbb {Z}$
be the largest integer such that
for all
![]() $k\leq K_0$
. Note that
$k\leq K_0$
. Note that
![]() $K_0$
only depends on the choice of
$K_0$
only depends on the choice of
![]() $\Lambda $
.
$\Lambda $
.
We define the norm
![]() $\| \;\cdot \; \|$
for the wedge product by
$\| \;\cdot \; \|$
for the wedge product by
For
![]() $\underline {k}=(k_1,\ldots ,k_s)\in \mathbb {Z}_{\ge K_0}^s$
and
$\underline {k}=(k_1,\ldots ,k_s)\in \mathbb {Z}_{\ge K_0}^s$
and
![]() $\underline {p}=(p_1,\ldots ,p_s)\in \mathbb {Z}_{\ge 0}^s$
, we denote by
$\underline {p}=(p_1,\ldots ,p_s)\in \mathbb {Z}_{\ge 0}^s$
, we denote by
![]() $\Lambda _{\underline {k}}(\underline {p})$
the set of
$\Lambda _{\underline {k}}(\underline {p})$
the set of
![]() $(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{k_1}\times \cdots \times \Lambda _{k_s}$
such that
$(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{k_1}\times \cdots \times \Lambda _{k_s}$
such that
 $$ \begin{align} {0<2^{-p_j-1}\|\mathbf{x}_j\| \bigg\|\bigwedge_{i=1}^{j-1}\mathbf{x}_i\bigg\|<\bigg\|\bigwedge_{i=1}^{j}\mathbf{x}_i\bigg\|\leq 2^{-p_j}\|\mathbf{x}_j\| \bigg\|\bigwedge_{i=1}^{j-1}\mathbf{x}_i\bigg\|} \end{align} $$
$$ \begin{align} {0<2^{-p_j-1}\|\mathbf{x}_j\| \bigg\|\bigwedge_{i=1}^{j-1}\mathbf{x}_i\bigg\|<\bigg\|\bigwedge_{i=1}^{j}\mathbf{x}_i\bigg\|\leq 2^{-p_j}\|\mathbf{x}_j\| \bigg\|\bigwedge_{i=1}^{j-1}\mathbf{x}_i\bigg\|} \end{align} $$
for
![]() $j=1,\ldots ,s$
. Then any
$j=1,\ldots ,s$
. Then any
![]() $(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{k_1}\times \cdots \times \Lambda _{k_s}$
such that
$(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{k_1}\times \cdots \times \Lambda _{k_s}$
such that
![]() $\mathbf {x}_1,\ldots ,\mathbf {x}_s$
are
$\mathbf {x}_1,\ldots ,\mathbf {x}_s$
are
![]() $\mathbb {R}$
-linearly independent is contained in
$\mathbb {R}$
-linearly independent is contained in
![]() $\bigcup _{\underline {p}\in \mathbb {Z}^s_{\ge 0}}\Lambda _{\underline {k}}(\underline {p})$
.
$\bigcup _{\underline {p}\in \mathbb {Z}^s_{\ge 0}}\Lambda _{\underline {k}}(\underline {p})$
.
Lemma 5.3. For any
![]() $\underline {k}\in \mathbb {Z}^s_{\ge K_0}$
and
$\underline {k}\in \mathbb {Z}^s_{\ge K_0}$
and
![]() $\underline {p}\in \mathbb {Z}^s_{\ge 0}$
,
$\underline {p}\in \mathbb {Z}^s_{\ge 0}$
,
 $$ \begin{align*}\#\Lambda_{\underline{k}}(\underline{p})\ll \prod_{j=1}^s 2^{\omega_s(k_j,p_j)},\end{align*} $$
$$ \begin{align*}\#\Lambda_{\underline{k}}(\underline{p})\ll \prod_{j=1}^s 2^{\omega_s(k_j,p_j)},\end{align*} $$
where
 $$ \begin{align*}\omega_s(k,p)= \begin{cases} dk-(d+1-s)p & \text{if}\ p\leq k,\\ sk-p & \text{if}\ p>k. \end{cases} \end{align*} $$
$$ \begin{align*}\omega_s(k,p)= \begin{cases} dk-(d+1-s)p & \text{if}\ p\leq k,\\ sk-p & \text{if}\ p>k. \end{cases} \end{align*} $$
Moreover, if there exists
![]() $1\leq j\leq s$
such that
$1\leq j\leq s$
such that
![]() $p_j\ge jk_j+K$
, then
$p_j\ge jk_j+K$
, then
![]() $\#\Lambda _{\underline {k}}(\underline {p})=0$
, where K is a sufficiently large constant depending only on the choice of lattice
$\#\Lambda _{\underline {k}}(\underline {p})=0$
, where K is a sufficiently large constant depending only on the choice of lattice
![]() $\Lambda $
.
$\Lambda $
.
Proof. Given
![]() $\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
, let V be the subspace spanned by
$\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
, let V be the subspace spanned by
![]() $\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
and denote by
$\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
and denote by
![]() $\Upsilon $
the region of
$\Upsilon $
the region of
![]() $\mathbf {x}_j$
satisfying
$\mathbf {x}_j$
satisfying
 $$ \begin{align*}\bigg\|\!\bigwedge_{i=1}^{j}\mathbf{x}_i\bigg\|\leq 2^{-p_j}\|\mathbf{x}_j\| \bigg\|\bigwedge_{i=1}^{j-1}\mathbf{x}_i\bigg\|.\end{align*} $$
$$ \begin{align*}\bigg\|\!\bigwedge_{i=1}^{j}\mathbf{x}_i\bigg\|\leq 2^{-p_j}\|\mathbf{x}_j\| \bigg\|\bigwedge_{i=1}^{j-1}\mathbf{x}_i\bigg\|.\end{align*} $$
Note that
![]() $\Upsilon \cap \mathcal {R}_k$
has width
$\Upsilon \cap \mathcal {R}_k$
has width
![]() $\asymp 2^{k_j}$
along the directions in V, and width
$\asymp 2^{k_j}$
along the directions in V, and width
![]() $\asymp 2^{k_j-p_j}$
along the directions perpendicular to V.
$\asymp 2^{k_j-p_j}$
along the directions perpendicular to V.
If
![]() $p_j\leq k_j$
, then the number of possible
$p_j\leq k_j$
, then the number of possible
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equation (5.9) is therefore at most
$\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equation (5.9) is therefore at most
![]() $\ll (2^{k_j})^{j-1}(2^{k_j-p_j})^{d-(j-1)}=2^{dk_j-(d+1-j)p_j}$
.
$\ll (2^{k_j})^{j-1}(2^{k_j-p_j})^{d-(j-1)}=2^{dk_j-(d+1-j)p_j}$
.
In the case
![]() $p_j> k_j$
, let
$p_j> k_j$
, let
![]() $j'$
be the maximal number of
$j'$
be the maximal number of
![]() $\mathbb {R}$
-linearly independent vectors in
$\mathbb {R}$
-linearly independent vectors in
![]() $\Upsilon \cap \Lambda _{k_j}$
. We may assume
$\Upsilon \cap \Lambda _{k_j}$
. We may assume
![]() $j\leq j'\leq d$
since there is no
$j\leq j'\leq d$
since there is no
![]() $\mathbf {x}_j$
satisfying equation (5.9) in
$\mathbf {x}_j$
satisfying equation (5.9) in
![]() $\Upsilon $
otherwise. Then we can take a
$\Upsilon $
otherwise. Then we can take a
![]() $j'$
-dimensional parallelepiped
$j'$
-dimensional parallelepiped
![]() $\mathcal {Q}$
generated by
$\mathcal {Q}$
generated by
![]() $\bar {\mathbf {x}}_1,\ldots ,\bar {\mathbf {x}}_{j'}\in \Upsilon \cap \Lambda _{k_j}$
such that there is no element of
$\bar {\mathbf {x}}_1,\ldots ,\bar {\mathbf {x}}_{j'}\in \Upsilon \cap \Lambda _{k_j}$
such that there is no element of
![]() $\Upsilon \cap \Lambda _{k_j}$
inside
$\Upsilon \cap \Lambda _{k_j}$
inside
![]() $\mathcal {Q}$
. Since
$\mathcal {Q}$
. Since
![]() $\bar {\mathbf {x}}_1,\ldots ,\bar {\mathbf {x}}_{j'}$
are
$\bar {\mathbf {x}}_1,\ldots ,\bar {\mathbf {x}}_{j'}$
are
![]() $\mathbb {R}$
-linearly independent and contained in
$\mathbb {R}$
-linearly independent and contained in ![]() , the
, the
![]() $j'$
-dimensional volume of
$j'$
-dimensional volume of ![]() is
is
![]() $\ge 1$
. Hence, the
$\ge 1$
. Hence, the
![]() $j'$
-dimensional volume of
$j'$
-dimensional volume of
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\gg 1$
independently of
$\gg 1$
independently of
![]() $p_j$
and
$p_j$
and
![]() $\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
. Also, the interior of the sets
$\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
. Also, the interior of the sets
![]() $\mathbf {x}_j+\mathcal {Q}$
with
$\mathbf {x}_j+\mathcal {Q}$
with
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
are pairwise disjoint. Note that
$\mathbf {x}_j\in \Lambda _{k_j}$
are pairwise disjoint. Note that
![]() $\mathcal {Q}$
is contained in
$\mathcal {Q}$
is contained in
![]() $j'(\Upsilon \cap \mathcal {R}_{k_j})$
since the generators are in
$j'(\Upsilon \cap \mathcal {R}_{k_j})$
since the generators are in
![]() $\Upsilon \cap \mathcal {R}_{k_j}$
. Thus, for any
$\Upsilon \cap \mathcal {R}_{k_j}$
. Thus, for any
![]() $\mathbf {x}_j\in \Upsilon \cap \Lambda _{k_j}$
, the set
$\mathbf {x}_j\in \Upsilon \cap \Lambda _{k_j}$
, the set
![]() $\mathbf {x}_j+\mathcal {Q}$
is contained in
$\mathbf {x}_j+\mathcal {Q}$
is contained in
![]() $(j'+1)(\Upsilon \cap \mathcal {R}_{k_j})$
and the
$(j'+1)(\Upsilon \cap \mathcal {R}_{k_j})$
and the
![]() $j'$
-dimensional volume of this region is
$j'$
-dimensional volume of this region is
Because of this and the uniform lower bound on the volume of
![]() $\mathcal {Q}$
, it follows that the number of possible
$\mathcal {Q}$
, it follows that the number of possible
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equation (5.9) is at most
$\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equation (5.9) is at most
![]() $\ll 2^{jk_j-p_j}$
. In particular, there is no such
$\ll 2^{jk_j-p_j}$
. In particular, there is no such
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
if
$\mathbf {x}_j\in \Lambda _{k_j}$
if
![]() $p_j\ge jk_j+K$
.
$p_j\ge jk_j+K$
.
We have shown that for fixed
![]() $\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
, the number of possible
$\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
, the number of possible
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equation (5.9) is
$\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equation (5.9) is
![]() $\ll 2^{\omega _j(k_j,p_j)}\leq 2^{\omega _s(k_j,p_j)}$
. Hence, the desired estimate follows.
$\ll 2^{\omega _j(k_j,p_j)}\leq 2^{\omega _s(k_j,p_j)}$
. Hence, the desired estimate follows.
For
![]() $\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}_{\ge 0}^s$
and
$\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}_{\ge 0}^s$
and
![]() $(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda ^s$
, let
$(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda ^s$
, let
![]() $\Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)$
be the set of
$\Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)$
be the set of
![]() ${\mathbf {y}\in \mathcal {K}=\mathrm {supp\,}\psi \subset [-1,1]^{d-1}}$
satisfying the following two conditions:
${\mathbf {y}\in \mathcal {K}=\mathrm {supp\,}\psi \subset [-1,1]^{d-1}}$
satisfying the following two conditions:
-
•
 for
for
 $i=1,\ldots ,s$
;
$i=1,\ldots ,s$
; -
•
 $|\boldsymbol {\beta }_i(\mathbf {y})|< 2^{-l_i}$
for
$|\boldsymbol {\beta }_i(\mathbf {y})|< 2^{-l_i}$
for
 $i=1,\ldots ,s$
.
$i=1,\ldots ,s$
.
Lemma 5.4. There exists
![]() $T_0\ge 0$
such that the following holds for any
$T_0\ge 0$
such that the following holds for any
![]() $t>T_0$
. For
$t>T_0$
. For
![]() $\underline {l}\in \mathbb {Z}_{\ge 0}^s$
and
$\underline {l}\in \mathbb {Z}_{\ge 0}^s$
and
![]() $(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda ^s$
, the set
$(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda ^s$
, the set
![]() $\Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)$
is the empty set if there exists
$\Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)$
is the empty set if there exists
![]() $1\leq i\leq s$
such that
$1\leq i\leq s$
such that
 $$ \begin{align*}\mathbf{x}_i\notin \bigcup_{k=K_0}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\Lambda_k.\end{align*} $$
$$ \begin{align*}\mathbf{x}_i\notin \bigcup_{k=K_0}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\Lambda_k.\end{align*} $$
If
![]() ${K_0\leq }k_i\leq \lfloor ({t}/{d\log 2})-l_i\rfloor $
for all
${K_0\leq }k_i\leq \lfloor ({t}/{d\log 2})-l_i\rfloor $
for all
![]() $1\leq i\leq s$
and
$1\leq i\leq s$
and
![]() $(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{\underline {k}}( \underline {p})$
, then
$(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{\underline {k}}( \underline {p})$
, then
 $$ \begin{align} {\operatorname{vol}_{\mathbb{R}^{d-1}}(\Omega_{\underline{l}}(\mathbf{x}_1,\ldots,\mathbf{x}_s))\ll e^{-({(d-1)s}/{d})t} \prod_{i=1}^s 2^{p_i-l_i-k_i}.} \end{align} $$
$$ \begin{align} {\operatorname{vol}_{\mathbb{R}^{d-1}}(\Omega_{\underline{l}}(\mathbf{x}_1,\ldots,\mathbf{x}_s))\ll e^{-({(d-1)s}/{d})t} \prod_{i=1}^s 2^{p_i-l_i-k_i}.} \end{align} $$
Proof. For
![]() $\mathbf {y}\in \Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)$
, by definition of
$\mathbf {y}\in \Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)$
, by definition of
![]() $\boldsymbol {\beta }_i(\mathbf {y})$
, we have
$\boldsymbol {\beta }_i(\mathbf {y})$
, we have
for
![]() $i=1,\ldots ,s$
. By a straightforward computation with
$i=1,\ldots ,s$
. By a straightforward computation with
![]() $\mathbf {x}_i=(\pi _1\mathbf {x}_i,\pi '\mathbf {x}_i)\in \mathbb {R}\times \mathbb {R}^{d-1}$
, it implies that
$\mathbf {x}_i=(\pi _1\mathbf {x}_i,\pi '\mathbf {x}_i)\in \mathbb {R}\times \mathbb {R}^{d-1}$
, it implies that
for
![]() $i=1,\ldots ,s$
.
$i=1,\ldots ,s$
.
If there exists i such that
![]() $\mathbf {x}_i\in \Lambda _{k_i}$
with
$\mathbf {x}_i\in \Lambda _{k_i}$
with
![]() $k_i>({t}/{d\log 2})-l_i$
, then it contradicts equation (5.12). If there exists i such that
$k_i>({t}/{d\log 2})-l_i$
, then it contradicts equation (5.12). If there exists i such that
![]() $\mathbf {x}_i\notin \bigcup _{k=K_0}^{\infty }\Lambda _k$
, then we have
$\mathbf {x}_i\notin \bigcup _{k=K_0}^{\infty }\Lambda _k$
, then we have
![]() $|\pi _1\mathbf {x}_i|>2|\pi '\mathbf {x}_i|$
, which also contradicts equations (5.11) and (5.12) since they imply
$|\pi _1\mathbf {x}_i|>2|\pi '\mathbf {x}_i|$
, which also contradicts equations (5.11) and (5.12) since they imply
This proves the first claim of the lemma.
Suppose now that
![]() $k_i\leq ({t}/{d\log 2})-l_i$
for all
$k_i\leq ({t}/{d\log 2})-l_i$
for all
![]() $i=1,\ldots ,s$
and
$i=1,\ldots ,s$
and
![]() $(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{\underline {k}}(\underline {p})$
. To prove the estimate in equation (5.10), we may assume
$(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{\underline {k}}(\underline {p})$
. To prove the estimate in equation (5.10), we may assume
![]() $\Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\neq \emptyset $
and pick any
$\Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\neq \emptyset $
and pick any
![]() $\mathbf {y}\in \Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)$
. Let
$\mathbf {y}\in \Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)$
. Let
![]() $p_1',\ldots ,p_s'\in \mathbb {Z}_{\ge 0}$
be the integers such that
$p_1',\ldots ,p_s'\in \mathbb {Z}_{\ge 0}$
be the integers such that
 $$ \begin{align*}2^{-p_j'-1}\bigg\|\bigwedge_{i=1}^{j-1} \frac{\pi'\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|< \bigg\|\bigwedge_{i=1}^j \frac{\pi'\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|\leq2^{-p_j'}\bigg\|\bigwedge_{i=1}^{j-1} \frac{\pi'\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|\end{align*} $$
$$ \begin{align*}2^{-p_j'-1}\bigg\|\bigwedge_{i=1}^{j-1} \frac{\pi'\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|< \bigg\|\bigwedge_{i=1}^j \frac{\pi'\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|\leq2^{-p_j'}\bigg\|\bigwedge_{i=1}^{j-1} \frac{\pi'\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|\end{align*} $$
for
![]() $j=1,\ldots ,s$
.
$j=1,\ldots ,s$
.
We will prove that
![]() $p_j'\leq p_j+O(1)$
for all
$p_j'\leq p_j+O(1)$
for all
![]() $1\leq j\leq s$
. Since
$1\leq j\leq s$
. Since
![]() ${\pi '\mathbf {x}_i}/{\|\pi '\mathbf {x}_i\|}$
terms are unit vectors, for each j, we can find
${\pi '\mathbf {x}_i}/{\|\pi '\mathbf {x}_i\|}$
terms are unit vectors, for each j, we can find
![]() $c_1,\ldots ,c_{j-1}\ll 1$
such that
$c_1,\ldots ,c_{j-1}\ll 1$
such that
 $$ \begin{align} {\bigg\|\frac{\pi'\mathbf{x}_j}{\|\pi'\mathbf{x}_j\|}-\sum_{i=1}^{j-1}c_i\frac{\pi'\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|\ll 2^{-p_j'}.} \end{align} $$
$$ \begin{align} {\bigg\|\frac{\pi'\mathbf{x}_j}{\|\pi'\mathbf{x}_j\|}-\sum_{i=1}^{j-1}c_i\frac{\pi'\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|\ll 2^{-p_j'}.} \end{align} $$
This in turn implies that for any choice of
![]() $\mathbf {y}$
,
$\mathbf {y}$
,
 $$ \begin{align} {\bigg|\frac{\pi'\mathbf{x}_j\cdot \mathbf{y}}{\|\pi'\mathbf{x}_j\|}-\sum_{i=1}^{j-1}c_i\frac{\pi'\mathbf{x}_i\cdot\mathbf{y}}{\|\pi'\mathbf{x}_i\|}\bigg|\ll 2^{-p_j'} \|\mathbf{y}\| .} \end{align} $$
$$ \begin{align} {\bigg|\frac{\pi'\mathbf{x}_j\cdot \mathbf{y}}{\|\pi'\mathbf{x}_j\|}-\sum_{i=1}^{j-1}c_i\frac{\pi'\mathbf{x}_i\cdot\mathbf{y}}{\|\pi'\mathbf{x}_i\|}\bigg|\ll 2^{-p_j'} \|\mathbf{y}\| .} \end{align} $$
Now, if
![]() $\mathbf {y}\in \Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)$
, then we have equation (5.11), and using the triangle inequality and
$\mathbf {y}\in \Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s)$
, then we have equation (5.11), and using the triangle inequality and
![]() $\|\pi '\mathbf {x}_i\|\gg 2^{k_i}$
, it follows that
$\|\pi '\mathbf {x}_i\|\gg 2^{k_i}$
, it follows that
 $$ \begin{align} {\bigg|\frac{\pi_1\mathbf{x}_j}{\|\pi'\mathbf{x}_j\|}-\sum_{i=1}^{j-1}c_i\frac{\pi_1\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg|\ll 2^{-p_j'}+\sum_{i=1}^{j}2^{-l_i-k_i}e^{-(({d-1})/{d})t}.} \end{align} $$
$$ \begin{align} {\bigg|\frac{\pi_1\mathbf{x}_j}{\|\pi'\mathbf{x}_j\|}-\sum_{i=1}^{j-1}c_i\frac{\pi_1\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg|\ll 2^{-p_j'}+\sum_{i=1}^{j}2^{-l_i-k_i}e^{-(({d-1})/{d})t}.} \end{align} $$
Combining equations (5.13) and (5.15), we get
 $$ \begin{align} {\bigg\|\frac{\mathbf{x}_j}{\|\pi'\mathbf{x}_j\|}-\sum_{i=1}^{j-1}c_i\frac{\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|\ll 2^{-p_j'}+\sum_{i=1}^{j}2^{-l_i-k_i}e^{-(({d-1})/{d})t},} \end{align} $$
$$ \begin{align} {\bigg\|\frac{\mathbf{x}_j}{\|\pi'\mathbf{x}_j\|}-\sum_{i=1}^{j-1}c_i\frac{\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|\ll 2^{-p_j'}+\sum_{i=1}^{j}2^{-l_i-k_i}e^{-(({d-1})/{d})t},} \end{align} $$
and hence
 $$ \begin{align} {\bigg\|\bigwedge_{i=1}^j \frac{\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|\ll\bigg(2^{-p_j'}+\sum_{i=1}^{j}2^{-l_i-k_i}e^{-(({d-1})/{d})t}\bigg)\bigg\|\bigwedge_{i=1}^{j-1} \frac{\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|} \end{align} $$
$$ \begin{align} {\bigg\|\bigwedge_{i=1}^j \frac{\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|\ll\bigg(2^{-p_j'}+\sum_{i=1}^{j}2^{-l_i-k_i}e^{-(({d-1})/{d})t}\bigg)\bigg\|\bigwedge_{i=1}^{j-1} \frac{\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|} \end{align} $$
for
![]() $j=1,\ldots ,s$
. Since
$j=1,\ldots ,s$
. Since
![]() $\|\pi '\mathbf {x}_i\|\asymp \|\mathbf {x}_i\|$
for all
$\|\pi '\mathbf {x}_i\|\asymp \|\mathbf {x}_i\|$
for all
![]() $i=1,\ldots ,s$
by definition of
$i=1,\ldots ,s$
by definition of
![]() $\Lambda _{k_i}$
terms, we can replace the
$\Lambda _{k_i}$
terms, we can replace the
![]() $\|\pi '\mathbf {x}_i\|$
terms in equation (5.17) with
$\|\pi '\mathbf {x}_i\|$
terms in equation (5.17) with
![]() $\|\mathbf {x}_i\|$
terms for
$\|\mathbf {x}_i\|$
terms for
![]() $i=1,\ldots ,j$
. By equation (5.9), it implies that
$i=1,\ldots ,j$
. By equation (5.9), it implies that
 $$ \begin{align} {2^{-p_j}\leq C\bigg(2^{-p_j'}+\sum_{i=1}^{j}2^{-l_i-k_i}e^{-(({d-1})/{d})t}\bigg)} \end{align} $$
$$ \begin{align} {2^{-p_j}\leq C\bigg(2^{-p_j'}+\sum_{i=1}^{j}2^{-l_i-k_i}e^{-(({d-1})/{d})t}\bigg)} \end{align} $$
for some constant
![]() $C>0$
.
$C>0$
.
However, we have
 $$ \begin{align*}\prod_{i=1}^{j}2^{k_i-p_i}\gg\prod_{i=1}^{j}2^{-p_i}\prod_{i=1}^{j}\|\mathbf{x}_j\|\asymp \bigg\|\bigwedge_{i=1}^{j}\mathbf{x}_i\bigg\|\ge 1,\end{align*} $$
$$ \begin{align*}\prod_{i=1}^{j}2^{k_i-p_i}\gg\prod_{i=1}^{j}2^{-p_i}\prod_{i=1}^{j}\|\mathbf{x}_j\|\asymp \bigg\|\bigwedge_{i=1}^{j}\mathbf{x}_i\bigg\|\ge 1,\end{align*} $$
and hence
![]() $p_j\leq \sum _{i=1}^{j}p_i\leq \sum _{i=1}^{j}k_i+O(1)$
for any
$p_j\leq \sum _{i=1}^{j}p_i\leq \sum _{i=1}^{j}k_i+O(1)$
for any
![]() $1\leq j\leq s$
. It follows that
$1\leq j\leq s$
. It follows that
![]() ${2^{-p_j}\gg 2^{-k_i}e^{-(({j-1})/{d})t}\geq 2^{-k_i}e^{-(({d-2})/{d})t}}$
for all
${2^{-p_j}\gg 2^{-k_i}e^{-(({j-1})/{d})t}\geq 2^{-k_i}e^{-(({d-2})/{d})t}}$
for all
![]() $1\leq i\leq j$
, so for C as above,
$1\leq i\leq j$
, so for C as above,
 $$ \begin{align} {2^{-p_j} \ge 2C\sum_{i=1}^{j}2^{-l_i-k_i}e^{-(({d-1})/{d})t}} \end{align} $$
$$ \begin{align} {2^{-p_j} \ge 2C\sum_{i=1}^{j}2^{-l_i-k_i}e^{-(({d-1})/{d})t}} \end{align} $$
holds for sufficiently large t. Combining with equation (5.18), we have
![]() $p_j'\leq p_j+O(1)$
for all
$p_j'\leq p_j+O(1)$
for all
![]() $1\leq j\leq s$
.
$1\leq j\leq s$
.
For each i, the set of
![]() $\mathbf {y}\in \mathcal {K}$
satisfying equation (5.11) is a
$\mathbf {y}\in \mathcal {K}$
satisfying equation (5.11) is a
![]() $2^{-l_i}e^{-(({d-1})/{d})t}\|\pi '\mathbf {x}_i\|^{-1}$
-thickened hyperplane in
$2^{-l_i}e^{-(({d-1})/{d})t}\|\pi '\mathbf {x}_i\|^{-1}$
-thickened hyperplane in
![]() $\mathbb {R}^{d-1}$
which is perpendicular to
$\mathbb {R}^{d-1}$
which is perpendicular to
![]() $\pi '\mathbf {x}_i$
. Therefore,
$\pi '\mathbf {x}_i$
. Therefore,
![]() $\operatorname {vol}_{\mathbb {R}^{d-1}}(\Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s))$
is the volume of the intersection of such s-number of hyperplanes and the compact set
$\operatorname {vol}_{\mathbb {R}^{d-1}}(\Omega _{\underline {l}}(\mathbf {x}_1,\ldots ,\mathbf {x}_s))$
is the volume of the intersection of such s-number of hyperplanes and the compact set
![]() $\mathcal {K}$
. The intersection has width
$\mathcal {K}$
. The intersection has width
![]() $\ll 2^{-l_i}e^{-(({d-1})/{d})t}\|\pi '\mathbf {x}_i\|^{-1}$
along the direction of
$\ll 2^{-l_i}e^{-(({d-1})/{d})t}\|\pi '\mathbf {x}_i\|^{-1}$
along the direction of
![]() $\pi '\mathbf {x}_i$
for
$\pi '\mathbf {x}_i$
for
![]() $1\leq i\leq s$
. It follows that the volume of the intersection is bounded above by
$1\leq i\leq s$
. It follows that the volume of the intersection is bounded above by
 $$ \begin{align*} &\!\!\!\!\!\!\!\!\!\!\ll \bigg\|\!\bigwedge_{i=1}^s \frac{\pi'\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|^{-1}\prod_{i=1}^s (2^{-l_i}e^{-(({d-1})/{d})t}\|\pi'\mathbf{x}_i\|^{-1})\\ &\!\!\!\!\!\!\!\!\!\!\ll \bigg(\prod_{i=1}^{s}2^{-p_i'}\bigg)^{-1}\prod_{i=1}^s (2^{-l_i}e^{-(({d-1})/{d})t}\|\mathbf{x}_i\|^{-1})\ll e^{-({(d-1)s}/{d})t}\prod_{i=1}^{s}2^{p_i-l_i-k_i}.\\[-51pt] \end{align*} $$
$$ \begin{align*} &\!\!\!\!\!\!\!\!\!\!\ll \bigg\|\!\bigwedge_{i=1}^s \frac{\pi'\mathbf{x}_i}{\|\pi'\mathbf{x}_i\|}\bigg\|^{-1}\prod_{i=1}^s (2^{-l_i}e^{-(({d-1})/{d})t}\|\pi'\mathbf{x}_i\|^{-1})\\ &\!\!\!\!\!\!\!\!\!\!\ll \bigg(\prod_{i=1}^{s}2^{-p_i'}\bigg)^{-1}\prod_{i=1}^s (2^{-l_i}e^{-(({d-1})/{d})t}\|\mathbf{x}_i\|^{-1})\ll e^{-({(d-1)s}/{d})t}\prod_{i=1}^{s}2^{p_i-l_i-k_i}.\\[-51pt] \end{align*} $$
Proof of Proposition 5.1 under hypothesis (B1)
By Lemma 5.2,
For
![]() $\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}_{\ge 0}^s$
, by Lemma 5.4, we have
$\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}_{\ge 0}^s$
, by Lemma 5.4, we have
 $$ \begin{align*} {\begin{aligned} &\operatorname{vol}_{\mathbb{R}^{d-1}}(\{\mathbf{y}\in\mathcal{K}: |\boldsymbol{\beta}_i(\mathbf{y})|<2^{-l_i}(i=1,\ldots,s)\})\\ &\quad=\sum_{(\mathbf{x}_1,\ldots,\mathbf{x}_s)\in\Lambda^s}\operatorname{vol}_{\mathbb{R}^{d-1}}(\Omega_{\underline{l}}(\mathbf{x}_1,\ldots,\mathbf{x}_s))\\ &\quad=\sum_{k_1=K_0}^{\lfloor({t}/{d\log 2})-l_1\rfloor}\cdots\sum_{k_s=K_0}^{\lfloor({t}/{d\log 2})-l_s\rfloor}\sum_{\underline{p}\in\mathbb{Z}_{\ge0}^s}\sum_{(\mathbf{x}_1,\ldots,\mathbf{x}_s)\in\Lambda_{\underline{k}}(\underline{p})}\operatorname{vol}_{\mathbb{R}^{d-1}}(\Omega_{\underline{l}}(\mathbf{x}_1,\ldots,\mathbf{x}_s))\\ &\quad\ll\sum_{k_1=K_0}^{\lfloor({t}/{d\log 2})-l_1\rfloor}\cdots\sum_{k_s=K_0}^{\lfloor({t}/{d\log 2})-l_s\rfloor}\sum_{\underline{p}\in\mathbb{Z}_{\ge0}^s}\#\Lambda_{\underline{k}}(\underline{p})e^{-({(d-1)s}/{d})t}\prod_{i=1}^{s}2^{p_i-l_i-k_i}.\end{aligned}} \end{align*} $$
$$ \begin{align*} {\begin{aligned} &\operatorname{vol}_{\mathbb{R}^{d-1}}(\{\mathbf{y}\in\mathcal{K}: |\boldsymbol{\beta}_i(\mathbf{y})|<2^{-l_i}(i=1,\ldots,s)\})\\ &\quad=\sum_{(\mathbf{x}_1,\ldots,\mathbf{x}_s)\in\Lambda^s}\operatorname{vol}_{\mathbb{R}^{d-1}}(\Omega_{\underline{l}}(\mathbf{x}_1,\ldots,\mathbf{x}_s))\\ &\quad=\sum_{k_1=K_0}^{\lfloor({t}/{d\log 2})-l_1\rfloor}\cdots\sum_{k_s=K_0}^{\lfloor({t}/{d\log 2})-l_s\rfloor}\sum_{\underline{p}\in\mathbb{Z}_{\ge0}^s}\sum_{(\mathbf{x}_1,\ldots,\mathbf{x}_s)\in\Lambda_{\underline{k}}(\underline{p})}\operatorname{vol}_{\mathbb{R}^{d-1}}(\Omega_{\underline{l}}(\mathbf{x}_1,\ldots,\mathbf{x}_s))\\ &\quad\ll\sum_{k_1=K_0}^{\lfloor({t}/{d\log 2})-l_1\rfloor}\cdots\sum_{k_s=K_0}^{\lfloor({t}/{d\log 2})-l_s\rfloor}\sum_{\underline{p}\in\mathbb{Z}_{\ge0}^s}\#\Lambda_{\underline{k}}(\underline{p})e^{-({(d-1)s}/{d})t}\prod_{i=1}^{s}2^{p_i-l_i-k_i}.\end{aligned}} \end{align*} $$
Using the estimate of
![]() $\#\Lambda _{\underline {k}}(\underline {p})$
in Lemma 5.3, we get
$\#\Lambda _{\underline {k}}(\underline {p})$
in Lemma 5.3, we get
 $$ \begin{align*} &\!\ll e^{-({(d-1)s}/{d})t}\kern-2pt\prod_{i=1}^s\kern-2.5pt\bigg(\!\sum_{k_i={K_0}}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\kern-3.5pt\bigg(\kern-1.8pt\sum_{p_i=0}^{k_i}2^{dk_i-(d-s+1)p_i}2^{p_i-l_i-k_i}+\sum_{p_i=k_i+1}^{sk_i+K}\kern-1.2pt 2^{sk_i-p_i}2^{p_i-l_i-k_i}\kern-1.5pt\bigg)\!\kern-0.2pt\bigg)\\ &\!\ll e^{-({(d-1)s}/{d})t}\prod_{i=1}^s\bigg(\sum_{k_i=K_0}^{\lfloor({t}/{d\log 2})-l_i\rfloor} (2^{(d-1)k_i-l_i}+(sk_i+K)2^{(s-1)k_i-l_i})\bigg)\\ &\!\ll e^{-({(d-1)s}/{d})t}\prod_{i=1}^s\bigg(\sum_{k_i=K_0}^{\lfloor({t}/{d\log 2})-l_i\rfloor}2^{(d-1)k_i-l_i}\bigg)\ll 2^{-d\sum l_i}. \end{align*} $$
$$ \begin{align*} &\!\ll e^{-({(d-1)s}/{d})t}\kern-2pt\prod_{i=1}^s\kern-2.5pt\bigg(\!\sum_{k_i={K_0}}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\kern-3.5pt\bigg(\kern-1.8pt\sum_{p_i=0}^{k_i}2^{dk_i-(d-s+1)p_i}2^{p_i-l_i-k_i}+\sum_{p_i=k_i+1}^{sk_i+K}\kern-1.2pt 2^{sk_i-p_i}2^{p_i-l_i-k_i}\kern-1.5pt\bigg)\!\kern-0.2pt\bigg)\\ &\!\ll e^{-({(d-1)s}/{d})t}\prod_{i=1}^s\bigg(\sum_{k_i=K_0}^{\lfloor({t}/{d\log 2})-l_i\rfloor} (2^{(d-1)k_i-l_i}+(sk_i+K)2^{(s-1)k_i-l_i})\bigg)\\ &\!\ll e^{-({(d-1)s}/{d})t}\prod_{i=1}^s\bigg(\sum_{k_i=K_0}^{\lfloor({t}/{d\log 2})-l_i\rfloor}2^{(d-1)k_i-l_i}\bigg)\ll 2^{-d\sum l_i}. \end{align*} $$
Hence, combining with equation (5.6), for any
![]() $t,R>0$
and
$t,R>0$
and
![]() $\eta <d$
, we obtain
$\eta <d$
, we obtain
 $$ \begin{align} {\begin{aligned} &\bigg|\!\int_{\mathbf{y}\in\mathcal{K}}F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\,d\mathbf{y}\bigg|\\ &\quad\ll \sum_{s=1}^{d-1}\sum_{l=\lfloor\log_2 R\rfloor}^{\infty} l^{s-1}2^{-(d-\eta) l}\ll R^{-(d-\eta+o(1))}, \end{aligned}} \end{align} $$
$$ \begin{align} {\begin{aligned} &\bigg|\!\int_{\mathbf{y}\in\mathcal{K}}F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\,d\mathbf{y}\bigg|\\ &\quad\ll \sum_{s=1}^{d-1}\sum_{l=\lfloor\log_2 R\rfloor}^{\infty} l^{s-1}2^{-(d-\eta) l}\ll R^{-(d-\eta+o(1))}, \end{aligned}} \end{align} $$
which completes the proof.
Proof of Proposition 5.1 under hypothesis (B2)
Recall that
![]() $\Gamma '(1,\boldsymbol {\xi })M_0\widetilde {n}(\mathbf {y})\Phi _t$
in equation (5.4) is expressed as
$\Gamma '(1,\boldsymbol {\xi })M_0\widetilde {n}(\mathbf {y})\Phi _t$
in equation (5.4) is expressed as
For
![]() $1\leq s\leq d-1$
and
$1\leq s\leq d-1$
and
![]() $\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}_{\ge 0}^s$
with
$\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}_{\ge 0}^s$
with
![]() $l_1+\cdots +l_s=l$
, we define
$l_1+\cdots +l_s=l$
, we define
![]() ${\Xi ^s_{\underline {l}}\subseteq \mathcal {F}}$
as in equation (5.5) and
${\Xi ^s_{\underline {l}}\subseteq \mathcal {F}}$
as in equation (5.5) and
![]() $\Gamma _{\underline {l}}^{s,r}\subseteq \Gamma $
by
$\Gamma _{\underline {l}}^{s,r}\subseteq \Gamma $
by
where
![]() $\delta _{d,r}={c_d r}/{\delta _d}$
. For
$\delta _{d,r}={c_d r}/{\delta _d}$
. For
![]() $g=(1,\boldsymbol {\xi } \gamma (\mathbf {y}))h(\mathbf {y})$
with
$g=(1,\boldsymbol {\xi } \gamma (\mathbf {y}))h(\mathbf {y})$
with
![]() $h(\mathbf {y})\in \Xi _{\underline {l}}^s$
, we have
$h(\mathbf {y})\in \Xi _{\underline {l}}^s$
, we have
 $$ \begin{align*} F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)&=F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi} \gamma(\mathbf{y}))h(\mathbf{y}))\\ &\leq \delta_d^\eta2^{\eta l}\chi_{[R,\infty)}(\delta_d^\eta2^{\eta l})\prod_{i=1}^{s}\chi_{[-\delta_{d,r} 2^{-l_i},\delta_{d,r} 2^{-l_i}]}(b_i(g))\end{align*} $$
$$ \begin{align*} F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)&=F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi} \gamma(\mathbf{y}))h(\mathbf{y}))\\ &\leq \delta_d^\eta2^{\eta l}\chi_{[R,\infty)}(\delta_d^\eta2^{\eta l})\prod_{i=1}^{s}\chi_{[-\delta_{d,r} 2^{-l_i},\delta_{d,r} 2^{-l_i}]}(b_i(g))\end{align*} $$
since, by construction, we have
![]() $v_i(g) \geq \delta _d 2^{l_i}$
and thus
$v_i(g) \geq \delta _d 2^{l_i}$
and thus
![]() ${c_d r}/{v_i(g)} \leq \delta _{d,r} 2^{-l_i}$
. Since
${c_d r}/{v_i(g)} \leq \delta _{d,r} 2^{-l_i}$
. Since
![]() $|b_i(g)|=|(\boldsymbol {\xi }\gamma )\cdot \mathbf {e}_i|_{\mathbb {Z}}$
, the integral in equation (5.4) is bounded by
$|b_i(g)|=|(\boldsymbol {\xi }\gamma )\cdot \mathbf {e}_i|_{\mathbb {Z}}$
, the integral in equation (5.4) is bounded by
 $$ \begin{align} &\bigg|\!\int_{\mathbf{y}\in\mathcal{K}}F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\,d\mathbf{y}\bigg|\nonumber\\ &\ll\sum_{s=1}^{d-1}\sum_{l=\lfloor\log_2 R\rfloor}^{\infty} 2^{\eta l}\sum_{\substack{\underline{l}=(l_1,\ldots,l_s)\in\mathbb{Z}^s_{\ge0} \\ l_1+\cdots+l_s=l}} \operatorname{vol}_{\mathbb{R}^{d-1}}(\{\mathbf{y}\in\mathcal{K}: h(\mathbf{y})\in\Xi_{\underline{l}}^s, \gamma(\mathbf{y})\in \Gamma_{\underline{l}}^{s,r}\} ).\end{align} $$
$$ \begin{align} &\bigg|\!\int_{\mathbf{y}\in\mathcal{K}}F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\,d\mathbf{y}\bigg|\nonumber\\ &\ll\sum_{s=1}^{d-1}\sum_{l=\lfloor\log_2 R\rfloor}^{\infty} 2^{\eta l}\sum_{\substack{\underline{l}=(l_1,\ldots,l_s)\in\mathbb{Z}^s_{\ge0} \\ l_1+\cdots+l_s=l}} \operatorname{vol}_{\mathbb{R}^{d-1}}(\{\mathbf{y}\in\mathcal{K}: h(\mathbf{y})\in\Xi_{\underline{l}}^s, \gamma(\mathbf{y})\in \Gamma_{\underline{l}}^{s,r}\} ).\end{align} $$
This is the required improvement on equation (5.6).
The remaining task is thus to estimate the measure of the set of
![]() $\mathbf {y}\in \mathcal {K}$
such that
$\mathbf {y}\in \mathcal {K}$
such that
![]() ${h(\mathbf {y})\in \Xi _{\underline {l}}^s}$
and
${h(\mathbf {y})\in \Xi _{\underline {l}}^s}$
and
![]() $\gamma (\mathbf {y})\in \Gamma _{\underline {l}}^{s,r}$
. Recall that
$\gamma (\mathbf {y})\in \Gamma _{\underline {l}}^{s,r}$
. Recall that ![]() . From now on, we fix
. From now on, we fix
![]() $r>0$
as in equation (5.2) and no longer record the implicit dependence of constants on this parameter. For
$r>0$
as in equation (5.2) and no longer record the implicit dependence of constants on this parameter. For
![]() ${\underline {k}\in \mathbb {Z}_{\ge K_0}^s}$
,
${\underline {k}\in \mathbb {Z}_{\ge K_0}^s}$
,
![]() $\underline {l}\in \mathbb {Z}_{\ge 0}^s$
and
$\underline {l}\in \mathbb {Z}_{\ge 0}^s$
and
![]() $\underline {p}\in \mathbb {Z}_{\ge 0}^s$
, we denote by
$\underline {p}\in \mathbb {Z}_{\ge 0}^s$
, we denote by
![]() $\Lambda _{\underline {k}}^{\underline {l}}(\underline {p})$
the set of elements in
$\Lambda _{\underline {k}}^{\underline {l}}(\underline {p})$
the set of elements in
![]() $(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{\underline {k}}(\underline {p})$
satisfying
$(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{\underline {k}}(\underline {p})$
satisfying
for all
![]() $1\leq i\leq s$
. As we counted the number of lattice points of
$1\leq i\leq s$
. As we counted the number of lattice points of
![]() $\Lambda _{\underline {k}}(\underline {p})$
in Lemma 5.3, here we count the number of lattice points of
$\Lambda _{\underline {k}}(\underline {p})$
in Lemma 5.3, here we count the number of lattice points of
![]() $\Lambda _{\underline {k}}^{\underline {l}}(\underline {p})$
as follows.
$\Lambda _{\underline {k}}^{\underline {l}}(\underline {p})$
as follows.
Lemma 5.5. For
![]() $\boldsymbol {\xi }\in \mathbb {R}^d$
, let
$\boldsymbol {\xi }\in \mathbb {R}^d$
, let
 $$ \begin{align*}&\omega_{s,\boldsymbol{\xi}}(k,p,l)\\&\quad= \begin{cases} dk-(d+1-s)p-d\log_2\dfrac{\zeta(\boldsymbol{\xi},2^{l-1})}{4\|M_0\|} & \text{if }p\leq k-\log_2\dfrac{\zeta(\boldsymbol{\xi},2^{l-1})}{4\|M_0\|},\\[6pt] (s-1)k-(s-1)\log_2\dfrac{\zeta(\boldsymbol{\xi},2^{l-1})}{4\|M_0\|} & \text{if }0\leq k-\log_2\dfrac{\zeta(\boldsymbol{\xi},2^{l-1})}{4\|M_0\|}<p\leq k,\\ sk-p & \text{if}\ p>k. \end{cases} \end{align*} $$
$$ \begin{align*}&\omega_{s,\boldsymbol{\xi}}(k,p,l)\\&\quad= \begin{cases} dk-(d+1-s)p-d\log_2\dfrac{\zeta(\boldsymbol{\xi},2^{l-1})}{4\|M_0\|} & \text{if }p\leq k-\log_2\dfrac{\zeta(\boldsymbol{\xi},2^{l-1})}{4\|M_0\|},\\[6pt] (s-1)k-(s-1)\log_2\dfrac{\zeta(\boldsymbol{\xi},2^{l-1})}{4\|M_0\|} & \text{if }0\leq k-\log_2\dfrac{\zeta(\boldsymbol{\xi},2^{l-1})}{4\|M_0\|}<p\leq k,\\ sk-p & \text{if}\ p>k. \end{cases} \end{align*} $$
For any
![]() $\underline {k}\in \mathbb {Z}_{\ge K_0}^s$
,
$\underline {k}\in \mathbb {Z}_{\ge K_0}^s$
,
![]() $\underline {l}\in \mathbb {Z}_{\ge 0}^s$
and
$\underline {l}\in \mathbb {Z}_{\ge 0}^s$
and
![]() $\underline {p}\in \mathbb {Z}^s_{\ge 0}$
,
$\underline {p}\in \mathbb {Z}^s_{\ge 0}$
,
 $$ \begin{align*}\#\Lambda_{\underline{k}}^{\underline{l}}(\underline{p})\ll \prod_{j=1}^{s}2^{\omega_{s,\boldsymbol{\xi}}(k_j,p_j,l_j)}.\end{align*} $$
$$ \begin{align*}\#\Lambda_{\underline{k}}^{\underline{l}}(\underline{p})\ll \prod_{j=1}^{s}2^{\omega_{s,\boldsymbol{\xi}}(k_j,p_j,l_j)}.\end{align*} $$
Moreover, if there exists
![]() $1\leq j\leq s$
such that
$1\leq j\leq s$
such that
![]() $p_j\ge jk_j+K$
or
$p_j\ge jk_j+K$
or
![]() $k_j<\log _2({\zeta (\boldsymbol {\xi },2^{l-1})}/ {4\|M_0\|})$
, then
$k_j<\log _2({\zeta (\boldsymbol {\xi },2^{l-1})}/ {4\|M_0\|})$
, then
![]() $\#\Lambda _{\underline {k}}(\underline {p})=0$
. Here, K is a sufficiently large constant depending on the choice of lattice
$\#\Lambda _{\underline {k}}(\underline {p})=0$
. Here, K is a sufficiently large constant depending on the choice of lattice
![]() $\Lambda $
.
$\Lambda $
.
Proof. For
![]() $(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{\underline {k}}^{\underline {l}}(p)\subseteq \Lambda _{\underline {k}}(p)$
, recall that
$(\mathbf {x}_1,\ldots ,\mathbf {x}_s)\in \Lambda _{\underline {k}}^{\underline {l}}(p)\subseteq \Lambda _{\underline {k}}(p)$
, recall that
 $$ \begin{align} {\bigg\|\bigwedge_{i=1}^{j}\mathbf{x}_i\bigg\|\leq 2^{-p_j}\|\mathbf{x}_j\|\bigg\|\bigwedge_{i=1}^{j-1}\mathbf{x}_i\bigg\|} \end{align} $$
$$ \begin{align} {\bigg\|\bigwedge_{i=1}^{j}\mathbf{x}_i\bigg\|\leq 2^{-p_j}\|\mathbf{x}_j\|\bigg\|\bigwedge_{i=1}^{j-1}\mathbf{x}_i\bigg\|} \end{align} $$
for
![]() $j=1,\ldots ,s$
. Given
$j=1,\ldots ,s$
. Given
![]() $\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
, in the proof of Lemma 5.3, we already showed that the possible number of
$\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
, in the proof of Lemma 5.3, we already showed that the possible number of
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
is
$\mathbf {x}_j\in \Lambda _{k_j}$
is
![]() $\ll 2^{\omega _s(k_j,p_j)}=2^{sk_j-p_j}$
if
$\ll 2^{\omega _s(k_j,p_j)}=2^{sk_j-p_j}$
if
![]() $p_j>k_j$
. Hence, it is enough to show that this bound can be improved under the assumption
$p_j>k_j$
. Hence, it is enough to show that this bound can be improved under the assumption
![]() $p_j\leq k_j$
.
$p_j\leq k_j$
.
We first consider the case
![]() $p_j\leq k_j-\log _2({\zeta (\boldsymbol {\xi },2^{l-1})}/{4\|M_0\|})$
. In this case, if
$p_j\leq k_j-\log _2({\zeta (\boldsymbol {\xi },2^{l-1})}/{4\|M_0\|})$
. In this case, if
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
satisfies equation (5.25), then
$\mathbf {x}_j\in \Lambda _{k_j}$
satisfies equation (5.25), then
![]() $\mathbf {x}_j$
must be
$\mathbf {x}_j$
must be
![]() $\ll 2^{k_j-p_j}$
-close to the subspace V spanned by
$\ll 2^{k_j-p_j}$
-close to the subspace V spanned by
![]() $\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
. Hence, the region of
$\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
. Hence, the region of
![]() $\mathbf {x}_j$
satisfying equation (5.25) has width
$\mathbf {x}_j$
satisfying equation (5.25) has width
![]() $2^{k_j-p_j}$
along the directions perpendicular to V and width
$2^{k_j-p_j}$
along the directions perpendicular to V and width
![]() $2^{k_j}$
along the directions of V. This region can be covered with at most
$2^{k_j}$
along the directions of V. This region can be covered with at most
cubes with sidelength
![]() $\|M_0\|^{-1}\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})$
.
$\|M_0\|^{-1}\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})$
.
We claim that there is at most one point of
![]() $\Lambda _{k_j}$
satisfying equation (5.24) in each cube with sidelength
$\Lambda _{k_j}$
satisfying equation (5.24) in each cube with sidelength
![]() $\|M_0\|^{-1}\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})$
. To see this, suppose that there are two distinct points
$\|M_0\|^{-1}\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})$
. To see this, suppose that there are two distinct points
![]() $\mathbf {x},\mathbf {x}'\in \Lambda _{k_j}$
with distance
$\mathbf {x},\mathbf {x}'\in \Lambda _{k_j}$
with distance
![]() $< \|M_0\|^{-1}\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})$
satisfying equation (5.24). Then we have
$< \|M_0\|^{-1}\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})$
satisfying equation (5.24). Then we have ![]() and
and
However, by the definition in equation (1.2), there is no
![]() $\mathbf {m}\in \mathbb {Z}^d\setminus \{0\}$
with
$\mathbf {m}\in \mathbb {Z}^d\setminus \{0\}$
with
![]() $|\mathbf {m}|<\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})$
and
$|\mathbf {m}|<\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})$
and
![]() $|\boldsymbol {\xi }\cdot \mathbf {m}|_{\mathbb {Z}}\leq \delta _{d,r}2^{-l_j+1}$
. Hence, the claim is proved. It follows from the claim that the number of possible
$|\boldsymbol {\xi }\cdot \mathbf {m}|_{\mathbb {Z}}\leq \delta _{d,r}2^{-l_j+1}$
. Hence, the claim is proved. It follows from the claim that the number of possible
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equations (5.24) and (5.25) is at most
$\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equations (5.24) and (5.25) is at most
![]() $\ll 2^{dk_j-(d+1-j)p_j}({\zeta (\boldsymbol {\xi },2^{l_j-1})}/{4\|M_0\|})^{-d}= 2^{\omega _{s,\boldsymbol {\xi }}(k_j,p_j,l_j)}$
.
$\ll 2^{dk_j-(d+1-j)p_j}({\zeta (\boldsymbol {\xi },2^{l_j-1})}/{4\|M_0\|})^{-d}= 2^{\omega _{s,\boldsymbol {\xi }}(k_j,p_j,l_j)}$
.
We now consider the case
![]() $k_j-\log _2({\zeta (\boldsymbol {\xi },2^{l-1})}/{4\|M_0\|})<p_j\leq k_j$
. In this case, the region of
$k_j-\log _2({\zeta (\boldsymbol {\xi },2^{l-1})}/{4\|M_0\|})<p_j\leq k_j$
. In this case, the region of
![]() $\mathbf {x}_j$
satisfying equation (5.25) can be covered with at most
$\mathbf {x}_j$
satisfying equation (5.25) can be covered with at most
cubes with sidelength
![]() $\|M_0\|^{-1}\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})$
since this region has width
$\|M_0\|^{-1}\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})$
since this region has width
![]() $2^{k_j-p_j}< {\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})}/{4\|M_0\|}$
along the directions perpendicular to V and width
$2^{k_j-p_j}< {\zeta (\boldsymbol {\xi },\delta _{d,r}^{-1}2^{l_j-1})}/{4\|M_0\|}$
along the directions perpendicular to V and width
![]() $2^{k_j}$
along the directions of V. Similar to the previous case, the number of possible
$2^{k_j}$
along the directions of V. Similar to the previous case, the number of possible
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equations (5.24) and (5.25) is at most
$\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equations (5.24) and (5.25) is at most
 $$ \begin{align*}\ll\bigg(2^{k_j}\bigg(\frac{\zeta(\boldsymbol{\xi},2^{l_j-1})}{4\|M_0\|}\bigg)^{-1}\bigg)^{j-1}\leq \bigg(2^{k_j}\bigg(\frac{\zeta(\boldsymbol{\xi},2^{l_j-1})}{4\|M_0\|}\bigg)^{-1}\bigg)^{s-1}= 2^{\omega_{s,\boldsymbol{\xi}}(k_j,p_j,l_j)}.\end{align*} $$
$$ \begin{align*}\ll\bigg(2^{k_j}\bigg(\frac{\zeta(\boldsymbol{\xi},2^{l_j-1})}{4\|M_0\|}\bigg)^{-1}\bigg)^{j-1}\leq \bigg(2^{k_j}\bigg(\frac{\zeta(\boldsymbol{\xi},2^{l_j-1})}{4\|M_0\|}\bigg)^{-1}\bigg)^{s-1}= 2^{\omega_{s,\boldsymbol{\xi}}(k_j,p_j,l_j)}.\end{align*} $$
We have shown that for fixed
![]() $\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
, the number of possible
$\mathbf {x}_1,\ldots ,\mathbf {x}_{j-1}$
, the number of possible
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equations (5.24) and (5.25) is
$\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equations (5.24) and (5.25) is
![]() $\ll 2^{\omega _{s,\boldsymbol {\xi }}(k_j,p_j,l_j)}$
. Hence, we obtain the desired estimate.
$\ll 2^{\omega _{s,\boldsymbol {\xi }}(k_j,p_j,l_j)}$
. Hence, we obtain the desired estimate.
As we have shown in Lemma 5.3,
![]() $\#\Lambda _{\underline {k}}(\underline {p})=0$
if there exists
$\#\Lambda _{\underline {k}}(\underline {p})=0$
if there exists
![]() $1\leq j\leq s$
such that
$1\leq j\leq s$
such that
![]() ${p_j\geq jk_j+K}$
. However, if there exists
${p_j\geq jk_j+K}$
. However, if there exists
![]() $1\leq j\leq s$
such that
$1\leq j\leq s$
such that
![]() $k_j<\log _2({\zeta (\boldsymbol {\xi },2^{l-1})}/{4\|M_0\|})$
, then we have
$k_j<\log _2({\zeta (\boldsymbol {\xi },2^{l-1})}/{4\|M_0\|})$
, then we have ![]() since
since
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
. It follows that
$\mathbf {x}_j\in \Lambda _{k_j}$
. It follows that ![]() by definition of
by definition of
![]() $\zeta (\boldsymbol {\xi },T)$
. In other words, there is no
$\zeta (\boldsymbol {\xi },T)$
. In other words, there is no
![]() $\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equation (5.24), and hence
$\mathbf {x}_j\in \Lambda _{k_j}$
satisfying equation (5.24), and hence
![]() $\#\Lambda _{\underline {k}}(\underline {p})=0$
.
$\#\Lambda _{\underline {k}}(\underline {p})=0$
.
The rest of the argument is similar to the case (B1). By Lemmas 5.2 and 5.4, we have

for
![]() $\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}_{\ge 0}^s$
. Using the estimate of
$\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}_{\ge 0}^s$
. Using the estimate of
![]() $\#\Lambda _{\underline {k}}^{\underline {l}}(\underline {p})$
in Lemma 5.5, we obtain
$\#\Lambda _{\underline {k}}^{\underline {l}}(\underline {p})$
in Lemma 5.5, we obtain
 $$ \begin{align} &\operatorname{vol}_{\mathbb{R}^{d-1}}(\{\mathbf{y}\in\mathcal{K}: h(\mathbf{y})\in\Xi_{\underline{l}}^s, \gamma(\mathbf{y})\in\Gamma_{\underline{l}}^{s,r}\})\nonumber\\ &\quad\ll e^{-({(d-1)s}/{d})t}\prod_{i=1}^{s}\bigg(\sum_{k_i=K_0}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\sum_{p_i=0}^{sk_i+K}2^{\omega_{s,\boldsymbol{\xi}}(k_i,p_i,l_i)}2^{p_i-l_i-k_i}\bigg)\nonumber\\ &\quad=e^{-({(d-1)s}/{d})t}\prod_{i=1}^{s}\bigg(\sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\sum_{p_i=0}^{sk_i+K}2^{\omega_{s,\boldsymbol{\xi}}(k_i,p_i,l_i)}2^{p_i-l_i-k_i}\bigg). \end{align} $$
$$ \begin{align} &\operatorname{vol}_{\mathbb{R}^{d-1}}(\{\mathbf{y}\in\mathcal{K}: h(\mathbf{y})\in\Xi_{\underline{l}}^s, \gamma(\mathbf{y})\in\Gamma_{\underline{l}}^{s,r}\})\nonumber\\ &\quad\ll e^{-({(d-1)s}/{d})t}\prod_{i=1}^{s}\bigg(\sum_{k_i=K_0}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\sum_{p_i=0}^{sk_i+K}2^{\omega_{s,\boldsymbol{\xi}}(k_i,p_i,l_i)}2^{p_i-l_i-k_i}\bigg)\nonumber\\ &\quad=e^{-({(d-1)s}/{d})t}\prod_{i=1}^{s}\bigg(\sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\sum_{p_i=0}^{sk_i+K}2^{\omega_{s,\boldsymbol{\xi}}(k_i,p_i,l_i)}2^{p_i-l_i-k_i}\bigg). \end{align} $$
We may assume
 $$ \begin{align} {\frac{t}{d\log 2}-l_i>\log_2\frac{\zeta(\boldsymbol{\xi},2^{l_i-1})}{4\|M_0\|}} \end{align} $$
$$ \begin{align} {\frac{t}{d\log 2}-l_i>\log_2\frac{\zeta(\boldsymbol{\xi},2^{l_i-1})}{4\|M_0\|}} \end{align} $$
for all i since otherwise, the product over i is zero.
We split the double sum in the last line of equation (5.26) as follows:
 $$ \begin{align*} &\!\sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\sum_{p_i=0}^{sk_i+K}2^{\omega_{s,\boldsymbol{\xi}}(k_i,p_i,l_i)}2^{p_i-l_i-k_i}=\sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\\&\!\times\bigg(\sum_{p_i=0}^{k_i-\lfloor \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rfloor-1}2^{(d-1)k_i-(d-s)p_i-l_i-d\log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})} \\&\!+\kern-1.2pt\sum_{p_i=k_i-\lfloor \log_2({\zeta(\boldsymbol{\xi},\!2^{l_i-1})}/{4\|M_0\|})\rfloor}^{k_i}\kern-2pt2^{(s-2)k_i+p_i-l_i-(s-1)\log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})}\kern-1pt+\!\sum_{p_i=k_i+1}^{sk_i+K}\kern-2pt2^{(s-1)k_i-l_i}\!\bigg)\kern-0.6pt. \end{align*} $$
$$ \begin{align*} &\!\sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\sum_{p_i=0}^{sk_i+K}2^{\omega_{s,\boldsymbol{\xi}}(k_i,p_i,l_i)}2^{p_i-l_i-k_i}=\sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\\&\!\times\bigg(\sum_{p_i=0}^{k_i-\lfloor \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rfloor-1}2^{(d-1)k_i-(d-s)p_i-l_i-d\log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})} \\&\!+\kern-1.2pt\sum_{p_i=k_i-\lfloor \log_2({\zeta(\boldsymbol{\xi},\!2^{l_i-1})}/{4\|M_0\|})\rfloor}^{k_i}\kern-2pt2^{(s-2)k_i+p_i-l_i-(s-1)\log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})}\kern-1pt+\!\sum_{p_i=k_i+1}^{sk_i+K}\kern-2pt2^{(s-1)k_i-l_i}\!\bigg)\kern-0.6pt. \end{align*} $$
This is bounded above by
 $$ \begin{align*} &\ll \sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}(2^{(d-1)k_i-l_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-d}\\&\quad+2^{(s-1)k_i-l_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-(s-1)}+(sk_i+K)2^{(s-1)k_i-l_i})\\ &\ll \sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}(2^{(d-1)k_i-l_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-d}\\&\quad+2^{(s-1)k_i-l_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-(s-1)}+k_i2^{(d-2)k_i-l_i})\\&\ll e^{(({d-1})/{d})t}2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-d}+e^{(({s-1})/{d})t}2^{-sl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-(s-1)}+te^{(({d-2})/{d})t}2^{-(d-1)l_i}. \end{align*} $$
$$ \begin{align*} &\ll \sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}(2^{(d-1)k_i-l_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-d}\\&\quad+2^{(s-1)k_i-l_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-(s-1)}+(sk_i+K)2^{(s-1)k_i-l_i})\\ &\ll \sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}(2^{(d-1)k_i-l_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-d}\\&\quad+2^{(s-1)k_i-l_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-(s-1)}+k_i2^{(d-2)k_i-l_i})\\&\ll e^{(({d-1})/{d})t}2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-d}+e^{(({s-1})/{d})t}2^{-sl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-(s-1)}+te^{(({d-2})/{d})t}2^{-(d-1)l_i}. \end{align*} $$
In summary, we have established that
 $$ \begin{align} &e^{-(({d-1})/{d})t}\sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\sum_{p_i=0}^{sk_i+K}2^{\omega_{s,\boldsymbol{\xi}}(k_i,p_i,l_i)}2^{p_i-l_i-k_i}\nonumber\\ &\ll 2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-d}+e^{-(({d-s})/{d})t}2^{-sl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-(s-1)}+te^{-{t}/{d}}2^{-(d-1)l_i}\nonumber\\ &\ll 2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1}\kern-0.2pt)^{\kern-1pt-d}\kern1.2pt{+}\kern1.2pt 2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{\kern-1pt-(d-1)}\kern1.2pt{+}\kern1.2pt(l_i\kern1.2pt{+}\kern1.2pt\log_2\zeta(\boldsymbol{\xi},2^{l_i-1}\kern-0.2pt))2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1}\kern-0.2pt)^{\kern-1pt-1}\nonumber\\ &\ll (l_i+\log_2\zeta(\boldsymbol{\xi},2^{l_i-1}))2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-1} \ll l_i2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-1}. \end{align} $$
$$ \begin{align} &e^{-(({d-1})/{d})t}\sum_{k_i=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l_i-1})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{d\log 2})-l_i\rfloor}\sum_{p_i=0}^{sk_i+K}2^{\omega_{s,\boldsymbol{\xi}}(k_i,p_i,l_i)}2^{p_i-l_i-k_i}\nonumber\\ &\ll 2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-d}+e^{-(({d-s})/{d})t}2^{-sl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-(s-1)}+te^{-{t}/{d}}2^{-(d-1)l_i}\nonumber\\ &\ll 2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1}\kern-0.2pt)^{\kern-1pt-d}\kern1.2pt{+}\kern1.2pt 2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{\kern-1pt-(d-1)}\kern1.2pt{+}\kern1.2pt(l_i\kern1.2pt{+}\kern1.2pt\log_2\zeta(\boldsymbol{\xi},2^{l_i-1}\kern-0.2pt))2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1}\kern-0.2pt)^{\kern-1pt-1}\nonumber\\ &\ll (l_i+\log_2\zeta(\boldsymbol{\xi},2^{l_i-1}))2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-1} \ll l_i2^{-dl_i}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-1}. \end{align} $$
Here we have used that
![]() $e^{-{t}/{d}}< 2^{-l_i} 4\|M_0\| \zeta (\boldsymbol {\xi },2^{l_i-1})^{-1}$
and
$e^{-{t}/{d}}< 2^{-l_i} 4\|M_0\| \zeta (\boldsymbol {\xi },2^{l_i-1})^{-1}$
and
 $$ \begin{align*}\frac{t}{d}\,e^{-{t}/{d}}< \bigg(l_i+\log_2\frac{\zeta(\boldsymbol{\xi},2^{l_i-1})}{4\|M_0\|}\bigg)2^{-l_i} 4\|M_0\| \zeta(\boldsymbol{\xi},2^{l_i-1})^{-1}\end{align*} $$
$$ \begin{align*}\frac{t}{d}\,e^{-{t}/{d}}< \bigg(l_i+\log_2\frac{\zeta(\boldsymbol{\xi},2^{l_i-1})}{4\|M_0\|}\bigg)2^{-l_i} 4\|M_0\| \zeta(\boldsymbol{\xi},2^{l_i-1})^{-1}\end{align*} $$
for
![]() $t>d$
, both of which follow from equation (5.27). (Note that
$t>d$
, both of which follow from equation (5.27). (Note that
![]() $x\mapsto x 2^{-x}$
is strictly decreasing for
$x\mapsto x 2^{-x}$
is strictly decreasing for
![]() $x>{1}/{\log 2}$
.)
$x>{1}/{\log 2}$
.)
Combining equations (5.26) and (5.28), we have
 $$ \begin{align} {\operatorname{vol}_{\mathbb{R}^{d-1}}\bigg(\bigg\{\mathbf{y}\in\mathcal{K}: h(\mathbf{y})\in\Xi_{\underline{l}}^s, \gamma(\mathbf{y})\in\Gamma_{\underline{l}}^{s,r}\bigg\}\bigg)\ll l^s2^{-dl}\prod_{i=1}^{s}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-1}} \end{align} $$
$$ \begin{align} {\operatorname{vol}_{\mathbb{R}^{d-1}}\bigg(\bigg\{\mathbf{y}\in\mathcal{K}: h(\mathbf{y})\in\Xi_{\underline{l}}^s, \gamma(\mathbf{y})\in\Gamma_{\underline{l}}^{s,r}\bigg\}\bigg)\ll l^s2^{-dl}\prod_{i=1}^{s}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-1}} \end{align} $$
for any
![]() $\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}_{\ge 0}^{s}$
with
$\underline {l}=(l_1,\ldots ,l_s)\in \mathbb {Z}_{\ge 0}^{s}$
with
![]() $l_1+\cdots +l_s=l$
.
$l_1+\cdots +l_s=l$
.
For any
![]() $t,R>0$
, it follows from equations (5.23) and (5.29) that
$t,R>0$
, it follows from equations (5.23) and (5.29) that
 $$ \begin{align} & \bigg|\!\int_{\mathbf{y}\in[-1,1]^{d-1}} F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\,d\mathbf{y}\bigg| \nonumber\\ &\quad \ll \sum_{s=1}^{d-1} \sum_{l=\lfloor\log_2 R\rfloor}^{s\lfloor({t}/{d\log 2})\rfloor} \sum_{\substack{\underline{l}=(l_1,\ldots,l_s)\in\mathbb{Z}^s_{\ge0} \\ l_1+\cdots+l_s=l}} l^s 2^{(\eta-d)l}\prod_{i=1}^{s}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-1} \nonumber\\ &\quad \ll \sum_{s=1}^{d-1} \sum_{\substack{\underline{l}=(l_1,\ldots,l_s)\in\mathbb{Z}^s_{\ge0} \\ l_1+\cdots+l_s \geq \lfloor\log_2 R\rfloor }} \prod_{i=1}^{s} (l_i+1)^s 2^{(\eta-d)l_i} \zeta(\boldsymbol{\xi},2^{l_i-1})^{-1}. \end{align} $$
$$ \begin{align} & \bigg|\!\int_{\mathbf{y}\in[-1,1]^{d-1}} F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\,d\mathbf{y}\bigg| \nonumber\\ &\quad \ll \sum_{s=1}^{d-1} \sum_{l=\lfloor\log_2 R\rfloor}^{s\lfloor({t}/{d\log 2})\rfloor} \sum_{\substack{\underline{l}=(l_1,\ldots,l_s)\in\mathbb{Z}^s_{\ge0} \\ l_1+\cdots+l_s=l}} l^s 2^{(\eta-d)l}\prod_{i=1}^{s}\zeta(\boldsymbol{\xi},2^{l_i-1})^{-1} \nonumber\\ &\quad \ll \sum_{s=1}^{d-1} \sum_{\substack{\underline{l}=(l_1,\ldots,l_s)\in\mathbb{Z}^s_{\ge0} \\ l_1+\cdots+l_s \geq \lfloor\log_2 R\rfloor }} \prod_{i=1}^{s} (l_i+1)^s 2^{(\eta-d)l_i} \zeta(\boldsymbol{\xi},2^{l_i-1})^{-1}. \end{align} $$
Since the final bound of equation (5.30) is independent of t and
 $$ \begin{align*} \sum_{(l_1,\ldots,l_s)\in\mathbb{Z}^s_{\ge0}} \prod_{i=0}^{s} (l_i+1)^s 2^{(\eta-d)l_i} \zeta(\boldsymbol{\xi},2^{l_i-1})^{-1} = \bigg( \sum_{l=0}^\infty (l+1)^s 2^{(\eta-d)l} \zeta(\boldsymbol{\xi},2^{l-1})^{-1} \bigg)^{\kern-0.7pts} \kern1.3pt{<}\kern1.3pt\infty \end{align*} $$
$$ \begin{align*} \sum_{(l_1,\ldots,l_s)\in\mathbb{Z}^s_{\ge0}} \prod_{i=0}^{s} (l_i+1)^s 2^{(\eta-d)l_i} \zeta(\boldsymbol{\xi},2^{l_i-1})^{-1} = \bigg( \sum_{l=0}^\infty (l+1)^s 2^{(\eta-d)l} \zeta(\boldsymbol{\xi},2^{l-1})^{-1} \bigg)^{\kern-0.7pts} \kern1.3pt{<}\kern1.3pt\infty \end{align*} $$
converges by assumption (B2) (note
![]() $s\leq d-1$
), we can conclude that
$s\leq d-1$
), we can conclude that
 $$ \begin{align*} {\begin{aligned} \lim_{R\to\infty}\limsup_{t\to \infty}&\bigg|\!\int_{\mathbf{y}\in[-1,1]^{d-1}} F_{R,\eta,r}\bigg(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t\bigg) \,d\mathbf{y}\bigg| =0, \end{aligned}} \end{align*} $$
$$ \begin{align*} {\begin{aligned} \lim_{R\to\infty}\limsup_{t\to \infty}&\bigg|\!\int_{\mathbf{y}\in[-1,1]^{d-1}} F_{R,\eta,r}\bigg(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t\bigg) \,d\mathbf{y}\bigg| =0, \end{aligned}} \end{align*} $$
as required.
We now discuss the case where
![]() $d=2$
and
$d=2$
and
![]() $\boldsymbol {\xi }$
is
$\boldsymbol {\xi }$
is
![]() $(0,\eta -2,2)$
-vaguely Diophantine. If
$(0,\eta -2,2)$
-vaguely Diophantine. If
![]() $d=2$
, then
$d=2$
, then
![]() $s=1$
, and in view of the definition in equation (5.9), the set
$s=1$
, and in view of the definition in equation (5.9), the set
![]() $\Lambda _{k}(p)$
is the empty set unless
$\Lambda _{k}(p)$
is the empty set unless
![]() $p=0$
. Hence, the double sum in the last line of equation (5.26) is written as
$p=0$
. Hence, the double sum in the last line of equation (5.26) is written as
 $$ \begin{align*}\sum_{k=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{2\log 2})-l\rfloor}2^{\omega_{s,\boldsymbol{\xi}}(k,0,l)}2^{-l-k}=\sum_{k=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{2\log 2})-l\rfloor}2^{k-l}\zeta(\boldsymbol{\xi},2^{l-1})^{-2}\end{align*} $$
$$ \begin{align*}\sum_{k=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{2\log 2})-l\rfloor}2^{\omega_{s,\boldsymbol{\xi}}(k,0,l)}2^{-l-k}=\sum_{k=\lceil \log_2({\zeta(\boldsymbol{\xi},2^{l})}/{4\|M_0\|})\rceil}^{\lfloor({t}/{2\log 2})-l\rfloor}2^{k-l}\zeta(\boldsymbol{\xi},2^{l-1})^{-2}\end{align*} $$
and bounded above by
![]() $\ll e^{{t}/{2}}2^{-2l}\zeta (\boldsymbol {\xi },2^{l-1})^{-2}$
. Plugging this in equation (5.26), we get
$\ll e^{{t}/{2}}2^{-2l}\zeta (\boldsymbol {\xi },2^{l-1})^{-2}$
. Plugging this in equation (5.26), we get
Note that here we gained additional decay of
![]() $\zeta (\boldsymbol {\xi },2^{l-1})^{-1}$
in comparison to equation (5.29). It follows that
$\zeta (\boldsymbol {\xi },2^{l-1})^{-1}$
in comparison to equation (5.29). It follows that
 $$ \begin{align*}\!\!\!\!\!\!\!\!\bigg|\!\int_{\mathbf{y}\in[-1,1]} F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\,d\mathbf{y}\bigg|\ll \sum_{l=\lfloor\log_2 R\rfloor}^{\lfloor{t}/{2\log 2}\rfloor} 2^{(\eta-2)l}\zeta(\boldsymbol{\xi},2^{l-1})^{-2}<\infty.\\[-46pt]\end{align*} $$
$$ \begin{align*}\!\!\!\!\!\!\!\!\bigg|\!\int_{\mathbf{y}\in[-1,1]} F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0\widetilde{n}(\mathbf{y})\Phi_t)\,d\mathbf{y}\bigg|\ll \sum_{l=\lfloor\log_2 R\rfloor}^{\lfloor{t}/{2\log 2}\rfloor} 2^{(\eta-2)l}\zeta(\boldsymbol{\xi},2^{l-1})^{-2}<\infty.\\[-46pt]\end{align*} $$
Lemma 5.6. For any compact set
![]() $\mathcal {C}\subset G$
, there exists
$\mathcal {C}\subset G$
, there exists
![]() $C=C(\mathcal {C})>1$
such that
$C=C(\mathcal {C})>1$
such that
![]() $F_{R,\eta ,r}(g(h,0))\leq C^{(d-1)\eta } F_{C^{-(d-1)}R,\eta ,Cr}(g)$
for any
$F_{R,\eta ,r}(g(h,0))\leq C^{(d-1)\eta } F_{C^{-(d-1)}R,\eta ,Cr}(g)$
for any
![]() $h\in \mathcal {C}$
and
$h\in \mathcal {C}$
and
![]() $g\in G'$
.
$g\in G'$
.
Proof. Let
![]() $g=(1,\mathbf {b})(M,0)$
with
$g=(1,\mathbf {b})(M,0)$
with
![]() $M\in G$
and
$M\in G$
and
![]() $\mathbf {b}\in \mathbb {R}^d$
. For each
$\mathbf {b}\in \mathbb {R}^d$
. For each
![]() $1\leq i\leq d$
, we have
$1\leq i\leq d$
, we have
![]() $v_i(g)=\|\mathbf {e}_i\mathbf {v}(M)\|=\|\mathbf {e}_iM\|$
and
$v_i(g)=\|\mathbf {e}_i\mathbf {v}(M)\|=\|\mathbf {e}_iM\|$
and
![]() $v_i(g(h,0))=\|\mathbf {e}_i\mathbf {v}(Mh)\|=\|\mathbf {e}_iMh\|$
, and hence there exists
$v_i(g(h,0))=\|\mathbf {e}_i\mathbf {v}(Mh)\|=\|\mathbf {e}_iMh\|$
, and hence there exists
![]() $C=C(\mathcal {C})>1$
such that
$C=C(\mathcal {C})>1$
such that
![]() $C^{-1}v_i(g(h,0))\leq v_i(g)\leq Cv_i(g(h,0))$
for any
$C^{-1}v_i(g(h,0))\leq v_i(g)\leq Cv_i(g(h,0))$
for any
![]() $h\in \mathcal {C}$
. We also have
$h\in \mathcal {C}$
. We also have
![]() $b_i(g)=b_i(g(h,0))$
for all i since
$b_i(g)=b_i(g(h,0))$
for all i since
![]() $b_i$
is invariant under
$b_i$
is invariant under
![]() $\operatorname {SL}(d,\mathbb {R})$
-action. Let
$\operatorname {SL}(d,\mathbb {R})$
-action. Let
![]() $g'=g(h,0)$
. It follows that
$g'=g(h,0)$
. It follows that
 $$ \begin{align*} &F_{R,\eta,r}(g')=\chi_{[R,\infty)}\bigg(\prod_{i=1}^{s_r(g')}v_i(g')\bigg)\; \prod_{i=1}^{s_r(g')} v_i(g')^\eta \chi_{[-c_dr,c_dr]}(v_i(g') b_i(g'))\\ &\quad\leq C^{(d-1)\eta}\chi_{[C^{-(d-1)}R,\infty)}\bigg(\prod_{i=1}^{s_r(g)}v_i(g)\bigg)\; \prod_{i=1}^{s_r(g)} v_i(g)^\eta \chi_{[-c_dCr,c_dCr]}(v_i(g) b_i(g))\\ &\quad=C^{(d-1)\eta}F_{C^{-(d-1)}R,\eta,Cr}(g).\\[-3.2pc] \end{align*} $$
$$ \begin{align*} &F_{R,\eta,r}(g')=\chi_{[R,\infty)}\bigg(\prod_{i=1}^{s_r(g')}v_i(g')\bigg)\; \prod_{i=1}^{s_r(g')} v_i(g')^\eta \chi_{[-c_dr,c_dr]}(v_i(g') b_i(g'))\\ &\quad\leq C^{(d-1)\eta}\chi_{[C^{-(d-1)}R,\infty)}\bigg(\prod_{i=1}^{s_r(g)}v_i(g)\bigg)\; \prod_{i=1}^{s_r(g)} v_i(g)^\eta \chi_{[-c_dCr,c_dCr]}(v_i(g) b_i(g))\\ &\quad=C^{(d-1)\eta}F_{C^{-(d-1)}R,\eta,Cr}(g).\\[-3.2pc] \end{align*} $$
Let us denote by
![]() $\mathbb {S}^{d-1}_+$
and
$\mathbb {S}^{d-1}_+$
and
![]() $\mathbb {S}^{d-1}_-$
the upper hemisphere and the lower hemisphere, respectively, that is,
$\mathbb {S}^{d-1}_-$
the upper hemisphere and the lower hemisphere, respectively, that is,
By the construction of the map in equation (3.4), k is smooth, and its differential is non-singular and bounded on
![]() $\mathbb {S}^{d-1}_+$
. For
$\mathbb {S}^{d-1}_+$
. For
![]() $\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}_+$
, we may write
$\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}_+$
, we may write

for
![]() $c(\boldsymbol {\upsilon })>0$
,
$c(\boldsymbol {\upsilon })>0$
,
![]() $\mathbf {w}(\boldsymbol {\upsilon })\in \mathbb {R}^{d-1}$
and
$\mathbf {w}(\boldsymbol {\upsilon })\in \mathbb {R}^{d-1}$
and
![]() $A(\boldsymbol {\upsilon })\in \operatorname {Mat}_{d-1,d-1}(\mathbb {R})$
. Note that
$A(\boldsymbol {\upsilon })\in \operatorname {Mat}_{d-1,d-1}(\mathbb {R})$
. Note that
![]() $\mathbf {y},c,\mathbf {w}$
and A are smooth and bounded on
$\mathbf {y},c,\mathbf {w}$
and A are smooth and bounded on
![]() $\mathbb {S}^{d-1}_+$
.
$\mathbb {S}^{d-1}_+$
.
Proposition 5.7. Let
![]() $\unicode{x3bb} $
be a Borel probability measure on
$\unicode{x3bb} $
be a Borel probability measure on
![]() $\mathbb {S}^{d-1}$
with continuous density,
$\mathbb {S}^{d-1}$
with continuous density,
![]() $\boldsymbol {\xi }\in \mathbb {R}^d$
and
$\boldsymbol {\xi }\in \mathbb {R}^d$
and
![]() $\eta>0$
so that hypothesis (B1) or (B2) holds. Then
$\eta>0$
so that hypothesis (B1) or (B2) holds. Then
 $$ \begin{align} {\lim_{R\to\infty}\limsup_{t\to \infty}\bigg|\!\int_{\boldsymbol{\upsilon}\in\mathbb{S}^{d-1}_+}F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0k(\boldsymbol{\upsilon})\Phi_t)\,d\unicode{x3bb}(\boldsymbol{\upsilon})\bigg|=0.} \end{align} $$
$$ \begin{align} {\lim_{R\to\infty}\limsup_{t\to \infty}\bigg|\!\int_{\boldsymbol{\upsilon}\in\mathbb{S}^{d-1}_+}F_{R,\eta,r}(\Gamma'(1,\boldsymbol{\xi})M_0k(\boldsymbol{\upsilon})\Phi_t)\,d\unicode{x3bb}(\boldsymbol{\upsilon})\bigg|=0.} \end{align} $$
Proof. This follows from Proposition 5.1 by the same argument as in the proof of [Reference Marklof and StrömbergssonMS10, Corollary 5.4]. We first observe that

Since
![]() $c,\mathbf {w}$
and A are bounded on
$c,\mathbf {w}$
and A are bounded on
![]() $\mathbb {S}^{d-1}_+$
, we may choose a compact set
$\mathbb {S}^{d-1}_+$
, we may choose a compact set
![]() $\mathcal {C}\subset G$
so that
$\mathcal {C}\subset G$
so that ![]() for any
for any
![]() $\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}_+$
. It follows from Lemma 5.6 that there exists
$\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}_+$
. It follows from Lemma 5.6 that there exists
![]() $C>1$
such that
$C>1$
such that
for any
![]() $\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}_+$
. As
$\boldsymbol {\upsilon }\in \mathbb {S}^{d-1}_+$
. As
![]() $\mathbf {y}$
is smooth, equation (5.32) follows from Proposition 5.1.
$\mathbf {y}$
is smooth, equation (5.32) follows from Proposition 5.1.
6. The main lemma
Lemma 6.1. Under the assumptions of Theorem 2.2,
Proof. We have
 $$ \begin{align*}|\mathbb{M}_\unicode{x3bb}(T,\underline{z})-\mathbb{M}_\unicode{x3bb}^{(K)}(T,\underline{z})|\leq\int_{\mathcal{N}_{c,T}(\sigma^*,\boldsymbol{\upsilon})\ge K}(\mathcal{N}_{c,T}(\sigma^*,\boldsymbol{\upsilon})+1)^{\operatorname{Re}(z_1)+\cdots+\operatorname{Re}(z_m)}\unicode{x3bb}(d\boldsymbol{\upsilon}),\end{align*} $$
$$ \begin{align*}|\mathbb{M}_\unicode{x3bb}(T,\underline{z})-\mathbb{M}_\unicode{x3bb}^{(K)}(T,\underline{z})|\leq\int_{\mathcal{N}_{c,T}(\sigma^*,\boldsymbol{\upsilon})\ge K}(\mathcal{N}_{c,T}(\sigma^*,\boldsymbol{\upsilon})+1)^{\operatorname{Re}(z_1)+\cdots+\operatorname{Re}(z_m)}\unicode{x3bb}(d\boldsymbol{\upsilon}),\end{align*} $$
where
![]() $\sigma ^*=\max _{1\leq j\leq m}\sigma _j$
. We now split the integral over the upper and lower hemispheres. The integral over the upper hemisphere
$\sigma ^*=\max _{1\leq j\leq m}\sigma _j$
. We now split the integral over the upper and lower hemispheres. The integral over the upper hemisphere
![]() $\mathbb {S}^{d-1}_+$
vanishes in the limit in view of Proposition 5.7, and the upper bounds in equations (3.5) and (5.3). The analogous statement for
$\mathbb {S}^{d-1}_+$
vanishes in the limit in view of Proposition 5.7, and the upper bounds in equations (3.5) and (5.3). The analogous statement for
![]() $\mathbb {S}^{d-1}_-$
follows by symmetry, since the quantity
$\mathbb {S}^{d-1}_-$
follows by symmetry, since the quantity
![]() $\mathcal {N}_{c,T}(\sigma ^*,\boldsymbol {\upsilon })$
for a given
$\mathcal {N}_{c,T}(\sigma ^*,\boldsymbol {\upsilon })$
for a given
![]() $\boldsymbol {\xi }$
has the same value as
$\boldsymbol {\xi }$
has the same value as
![]() $\mathcal {N}_{c,T}(\sigma ^*,-\boldsymbol {\upsilon })$
for
$\mathcal {N}_{c,T}(\sigma ^*,-\boldsymbol {\upsilon })$
for
![]() $-\boldsymbol {\xi }$
, with everything else (including
$-\boldsymbol {\xi }$
, with everything else (including
![]() $M_0$
) being fixed.
$M_0$
) being fixed.
This completes the proof of Theorem 2.2.
7. Proof of Corollaries 2.3 and 2.4
7.1. Proof of Corollary 2.3
We will need the following variant of Siegel’s formula.
Proposition 7.1. [Reference El-Baz, Marklof and VinogradovEMV15, Proposition 14]
If
![]() $F\in L^1(\mathbb {R}^d\times \mathbb {R}^d)$
, then
$F\in L^1(\mathbb {R}^d\times \mathbb {R}^d)$
, then
 $$ \begin{align*} {\int_{\Gamma'\backslash G'}\sum_{\mathbf{m}_1\neq\mathbf{m}_2\in\mathbb{Z}^d}F(\mathbf{m}_1 g,\mathbf{m}_2 g)\, dm_{\Gamma'\backslash G'}(g)=\int_{\mathbb{R}^d\times\mathbb{R}^d}F(\mathbf{x},\mathbf{y})\,d\mathbf{x}\,d\mathbf{y}.} \end{align*} $$
$$ \begin{align*} {\int_{\Gamma'\backslash G'}\sum_{\mathbf{m}_1\neq\mathbf{m}_2\in\mathbb{Z}^d}F(\mathbf{m}_1 g,\mathbf{m}_2 g)\, dm_{\Gamma'\backslash G'}(g)=\int_{\mathbb{R}^d\times\mathbb{R}^d}F(\mathbf{x},\mathbf{y})\,d\mathbf{x}\,d\mathbf{y}.} \end{align*} $$
Here (and below), we view
![]() $g=\iota (\Gamma ' g)\in G'$
as the representative of the coset
$g=\iota (\Gamma ' g)\in G'$
as the representative of the coset
![]() $\Gamma ' g$
in the fundamental domain
$\Gamma ' g$
in the fundamental domain
![]() $\mathcal {F}'$
.
$\mathcal {F}'$
.
For the proof of Corollary 2.3, we first prove
 $$ \begin{align} {\sum_{\underline{r}=(r_1,r_2)\in\mathbb{Z}^2_{\ge0}}r_1r_2E_{c}(\underline{r},\underline{\sigma})=\sigma_1\sigma_2+\min\{\sigma_1,\sigma_2\}} \end{align} $$
$$ \begin{align} {\sum_{\underline{r}=(r_1,r_2)\in\mathbb{Z}^2_{\ge0}}r_1r_2E_{c}(\underline{r},\underline{\sigma})=\sigma_1\sigma_2+\min\{\sigma_1,\sigma_2\}} \end{align} $$
for
![]() $\underline {\sigma }=(\sigma _1,\sigma _2)$
. To deduce equation (7.1), note that
$\underline {\sigma }=(\sigma _1,\sigma _2)$
. To deduce equation (7.1), note that
 $$ \begin{align*}\sum_{(r_1,r_2)\in\mathbb{Z}^2_{\ge0}}r_1r_2E_{c}(\underline{r},\underline{\sigma})=\int_{\Gamma'\backslash G'}\sum_{\mathbf{m}_1,\mathbf{m}_2\in\mathbb{Z}^d}\chi_{\mathfrak{C}_c(\sigma_1)}(\mathbf{m}_1 g)\chi_{\mathfrak{C}_c(\sigma_2)}(\mathbf{m}_2 g)\, dm_{\Gamma'\backslash G'}(g).\end{align*} $$
$$ \begin{align*}\sum_{(r_1,r_2)\in\mathbb{Z}^2_{\ge0}}r_1r_2E_{c}(\underline{r},\underline{\sigma})=\int_{\Gamma'\backslash G'}\sum_{\mathbf{m}_1,\mathbf{m}_2\in\mathbb{Z}^d}\chi_{\mathfrak{C}_c(\sigma_1)}(\mathbf{m}_1 g)\chi_{\mathfrak{C}_c(\sigma_2)}(\mathbf{m}_2 g)\, dm_{\Gamma'\backslash G'}(g).\end{align*} $$
Recall that for
![]() $\sigma>0$
, the area of
$\sigma>0$
, the area of
![]() $\mathfrak {C}_c(\sigma )$
is precisely
$\mathfrak {C}_c(\sigma )$
is precisely
![]() $\sigma $
. Applying Proposition 7.1, the off-diagonal part of the right-hand side is equal to
$\sigma $
. Applying Proposition 7.1, the off-diagonal part of the right-hand side is equal to
For the diagonal part, let
![]() $\mathfrak {C}=\mathfrak {C}_c(\sigma _1)\cap \mathfrak {C}_c(\sigma _2)$
and note that
$\mathfrak {C}=\mathfrak {C}_c(\sigma _1)\cap \mathfrak {C}_c(\sigma _2)$
and note that
![]() $\mathfrak {C}=\mathfrak {C}_c(\min \{\sigma _1,\sigma _2\})$
. Then the diagonal part is evaluated as follows:
$\mathfrak {C}=\mathfrak {C}_c(\min \{\sigma _1,\sigma _2\})$
. Then the diagonal part is evaluated as follows:
 $$ \begin{align*} {\begin{aligned} & \int_{\Gamma'\backslash G'}\sum_{\mathbf{m}\in\mathbb{Z}^d} \chi_{\mathfrak{C}}(\mathbf{m} g)\, dm_{\Gamma'\backslash G'}(g) \\ &\quad=\int_{\Gamma\backslash G}\sum_{\mathbf{m}\in\mathbb{Z}^d}\int_{\mathbb{Z}^d\backslash\mathbb{R}^d}\chi_{\mathfrak{C}}((\mathbf{m}+\boldsymbol{\xi})M)\,d\boldsymbol{\xi}\, dm_{\Gamma\backslash G}(M)\\ &\quad=\int_{\Gamma\backslash G}\int_{\mathbb{R}^d}\chi_{\mathfrak{C}}(\mathbf{x} M)\,d\mathbf{x}\,dm_{\Gamma\backslash G}(M)=\int_{\mathbb{R}^d}\chi_{\mathfrak{C}}(\mathbf{x})\,dx=\min\{\sigma_1,\sigma_2\}. \end{aligned}} \end{align*} $$
$$ \begin{align*} {\begin{aligned} & \int_{\Gamma'\backslash G'}\sum_{\mathbf{m}\in\mathbb{Z}^d} \chi_{\mathfrak{C}}(\mathbf{m} g)\, dm_{\Gamma'\backslash G'}(g) \\ &\quad=\int_{\Gamma\backslash G}\sum_{\mathbf{m}\in\mathbb{Z}^d}\int_{\mathbb{Z}^d\backslash\mathbb{R}^d}\chi_{\mathfrak{C}}((\mathbf{m}+\boldsymbol{\xi})M)\,d\boldsymbol{\xi}\, dm_{\Gamma\backslash G}(M)\\ &\quad=\int_{\Gamma\backslash G}\int_{\mathbb{R}^d}\chi_{\mathfrak{C}}(\mathbf{x} M)\,d\mathbf{x}\,dm_{\Gamma\backslash G}(M)=\int_{\mathbb{R}^d}\chi_{\mathfrak{C}}(\mathbf{x})\,dx=\min\{\sigma_1,\sigma_2\}. \end{aligned}} \end{align*} $$
This completes the proof of equation (7.1).
For the proof of Corollary 2.3, observe that for
![]() $z_1=z_2=1$
, one of the hypotheses of Theorem 2.2 holds under the assumption of Corollary 2.3. Combining equation (7.1) with property (b) above, Corollary 2.3 then follows from Theorem 2.2.
$z_1=z_2=1$
, one of the hypotheses of Theorem 2.2 holds under the assumption of Corollary 2.3. Combining equation (7.1) with property (b) above, Corollary 2.3 then follows from Theorem 2.2.
7.2. Proof of Corollary 2.4
In this section, we show that Corollary 2.3 implies Corollary 2.4. Throughout this section, we assume that the statement of Corollary 2.3 holds.
Lemma 7.2. Let
![]() $h\in \operatorname {C}(\mathbb {S}^{d-1})$
and
$h\in \operatorname {C}(\mathbb {S}^{d-1})$
and
![]() $\sigma _1,\sigma _2>0$
. Then
$\sigma _1,\sigma _2>0$
. Then
 $$ \begin{align}&\lim_{N\to\infty}\int_{\mathbb{S}^{d-1}}\sum_{\substack{j_1,j_2=1 \\ j_1\neq j_2}}^N\chi_{[0,\sigma_1]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_1},\boldsymbol{\alpha}))\chi_{[0,\sigma_2]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_2},\boldsymbol{\alpha}))h(\boldsymbol{\alpha})\,d\boldsymbol{\alpha}\nonumber\\&\quad=\sigma_1\sigma_2\int_{\mathbb{S}^{d-1}}h(\boldsymbol{\alpha})\,d\boldsymbol{\alpha}. \end{align} $$
$$ \begin{align}&\lim_{N\to\infty}\int_{\mathbb{S}^{d-1}}\sum_{\substack{j_1,j_2=1 \\ j_1\neq j_2}}^N\chi_{[0,\sigma_1]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_1},\boldsymbol{\alpha}))\chi_{[0,\sigma_2]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_2},\boldsymbol{\alpha}))h(\boldsymbol{\alpha})\,d\boldsymbol{\alpha}\nonumber\\&\quad=\sigma_1\sigma_2\int_{\mathbb{S}^{d-1}}h(\boldsymbol{\alpha})\,d\boldsymbol{\alpha}. \end{align} $$
Proof. By Corollary 2.3, the left-hand side of equation (7.2) without the restriction
![]() ${j_1\neq j_2}$
converges to
${j_1\neq j_2}$
converges to
However, the diagonal part
![]() $j_1=j_2$
of the left-hand side of equation (7.2) is
$j_1=j_2$
of the left-hand side of equation (7.2) is
 $$ \begin{align} {\int_{\mathbb{S}^{d-1}}\sum_{j=1}^N\chi_{[0,\min\{\sigma_1,\sigma_2\}]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j},\boldsymbol{\alpha}))h(\boldsymbol{\alpha})\,d\boldsymbol{\alpha}.} \end{align} $$
$$ \begin{align} {\int_{\mathbb{S}^{d-1}}\sum_{j=1}^N\chi_{[0,\min\{\sigma_1,\sigma_2\}]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j},\boldsymbol{\alpha}))h(\boldsymbol{\alpha})\,d\boldsymbol{\alpha}.} \end{align} $$
Since h is continuous and
![]() $\mathbf {d}(\boldsymbol {\alpha }_j,\boldsymbol {\alpha })\ll _{\sigma _1,\sigma _2} N^{-{1}/({d-1})}$
for any
$\mathbf {d}(\boldsymbol {\alpha }_j,\boldsymbol {\alpha })\ll _{\sigma _1,\sigma _2} N^{-{1}/({d-1})}$
for any
![]() $1\leq j\leq N$
, for any
$1\leq j\leq N$
, for any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $N_0$
such that for all
$N_0$
such that for all
![]() $N\ge N_0$
, we have
$N\ge N_0$
, we have
![]() $|h(\boldsymbol {\alpha }_j)-h(\boldsymbol {\alpha })|<\epsilon $
for any
$|h(\boldsymbol {\alpha }_j)-h(\boldsymbol {\alpha })|<\epsilon $
for any
![]() $\boldsymbol {\alpha }\in \mathbb {S}^{d-1}$
and
$\boldsymbol {\alpha }\in \mathbb {S}^{d-1}$
and
![]() $1\leq j\leq N$
. It follows that the integral in equation (7.4) is approximated by
$1\leq j\leq N$
. It follows that the integral in equation (7.4) is approximated by
 $$ \begin{align} {\int_{\mathbb{S}^{d-1}}\sum_{j=1}^N\chi_{[0,\min\{\sigma_1,\sigma_2\}]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j},\boldsymbol{\alpha}))h(\boldsymbol{\alpha}_j)\,d\boldsymbol{\alpha}} \end{align} $$
$$ \begin{align} {\int_{\mathbb{S}^{d-1}}\sum_{j=1}^N\chi_{[0,\min\{\sigma_1,\sigma_2\}]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j},\boldsymbol{\alpha}))h(\boldsymbol{\alpha}_j)\,d\boldsymbol{\alpha}} \end{align} $$
up to error
![]() $<\epsilon \min \{\sigma _1,\sigma _2\}$
. Hence, equation (7.4) converges to
$<\epsilon \min \{\sigma _1,\sigma _2\}$
. Hence, equation (7.4) converges to
 $$ \begin{align} {\begin{aligned} &\lim_{N\to\infty}\int_{\mathbb{S}^{d-1}}\sum_{j=1}^N\chi_{[0,\min\{\sigma_1,\sigma_2\}]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j},\boldsymbol{\alpha}))h(\boldsymbol{\alpha})\,d\boldsymbol{\alpha}\\&\quad=\lim_{N\to\infty}\min\{\sigma_1,\sigma_2\}N^{-1}\sum_{j=1}^N h(\boldsymbol{\alpha}_j)\\ &\quad=\min\{\sigma_1,\sigma_2\}\int_{\mathbb{S}^{d-1}}h(\boldsymbol{\alpha})\,d\boldsymbol{\alpha} , \end{aligned}} \end{align} $$
$$ \begin{align} {\begin{aligned} &\lim_{N\to\infty}\int_{\mathbb{S}^{d-1}}\sum_{j=1}^N\chi_{[0,\min\{\sigma_1,\sigma_2\}]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j},\boldsymbol{\alpha}))h(\boldsymbol{\alpha})\,d\boldsymbol{\alpha}\\&\quad=\lim_{N\to\infty}\min\{\sigma_1,\sigma_2\}N^{-1}\sum_{j=1}^N h(\boldsymbol{\alpha}_j)\\ &\quad=\min\{\sigma_1,\sigma_2\}\int_{\mathbb{S}^{d-1}}h(\boldsymbol{\alpha})\,d\boldsymbol{\alpha} , \end{aligned}} \end{align} $$
since the
![]() $\boldsymbol {\alpha }_j$
terms are uniformly distributed over
$\boldsymbol {\alpha }_j$
terms are uniformly distributed over
![]() $\mathbb {S}^{d-1}$
. Therefore, the second summand of equation (7.3) is the off-diagonal contribution appearing in equation (7.2), as desired.
$\mathbb {S}^{d-1}$
. Therefore, the second summand of equation (7.3) is the off-diagonal contribution appearing in equation (7.2), as desired.
Lemma 7.3. Let
![]() $g\in \operatorname {C}(\mathbb {S}^{d-1}\times \mathbb {S}^{d-1})$
and
$g\in \operatorname {C}(\mathbb {S}^{d-1}\times \mathbb {S}^{d-1})$
and
![]() $\sigma _1,\sigma _2>0$
. Then
$\sigma _1,\sigma _2>0$
. Then
 $$ \begin{align} &\lim_{N\to\infty}\!\sum_{\substack{j_1,j_2=1\\ j_1\neq j_2}}^N\!g(\boldsymbol{\alpha}_{j_1},\boldsymbol{\alpha}_{j_2})\int_{\mathbb{S}^{d-1}}\!\chi_{[0,\sigma_1]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_1},\boldsymbol{\alpha}))\chi_{[0,\sigma_2]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_2},\boldsymbol{\alpha}))\,d\boldsymbol{\alpha}\nonumber\\&\quad=\sigma_1\sigma_2\int_{\mathbb{S}^{d-1}}g(\boldsymbol{\alpha},\boldsymbol{\alpha})\,d\boldsymbol{\alpha}. \end{align} $$
$$ \begin{align} &\lim_{N\to\infty}\!\sum_{\substack{j_1,j_2=1\\ j_1\neq j_2}}^N\!g(\boldsymbol{\alpha}_{j_1},\boldsymbol{\alpha}_{j_2})\int_{\mathbb{S}^{d-1}}\!\chi_{[0,\sigma_1]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_1},\boldsymbol{\alpha}))\chi_{[0,\sigma_2]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_2},\boldsymbol{\alpha}))\,d\boldsymbol{\alpha}\nonumber\\&\quad=\sigma_1\sigma_2\int_{\mathbb{S}^{d-1}}g(\boldsymbol{\alpha},\boldsymbol{\alpha})\,d\boldsymbol{\alpha}. \end{align} $$
Proof. Since g is continuous and
![]() $\mathbf {d}(\boldsymbol {\alpha }_j,\boldsymbol {\alpha })\ll _{\sigma _1,\sigma _2}N^{-{1}/({d-1})}$
for any
$\mathbf {d}(\boldsymbol {\alpha }_j,\boldsymbol {\alpha })\ll _{\sigma _1,\sigma _2}N^{-{1}/({d-1})}$
for any
![]() $1\leq j\leq N$
, for any
$1\leq j\leq N$
, for any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $N_0$
such that for all
$N_0$
such that for all
![]() $N\geq N_0$
, we have
$N\geq N_0$
, we have
![]() $|g(\boldsymbol {\alpha },\boldsymbol {\alpha })-g(\boldsymbol {\alpha }_{j_1},\boldsymbol {\alpha }_{j_2})|<\epsilon $
for any
$|g(\boldsymbol {\alpha },\boldsymbol {\alpha })-g(\boldsymbol {\alpha }_{j_1},\boldsymbol {\alpha }_{j_2})|<\epsilon $
for any
![]() $\boldsymbol {\alpha }\in \mathbb {S}^{d-1}$
and
$\boldsymbol {\alpha }\in \mathbb {S}^{d-1}$
and
![]() $1\leq j_1,j_2\leq N$
. It follows that the left-hand side of equation (7.7) is approximated by
$1\leq j_1,j_2\leq N$
. It follows that the left-hand side of equation (7.7) is approximated by
 $$ \begin{align} {\sum_{\substack{j_1,j_2=1\\ j_1\neq j_2}}^N\int_{\mathbb{S}^{d-1}}g(\boldsymbol{\alpha},\boldsymbol{\alpha})\chi_{[0,\sigma_1]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_1},\boldsymbol{\alpha}))\chi_{[0,\sigma_2]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_2},\boldsymbol{\alpha}))\,d\boldsymbol{\alpha}} \end{align} $$
$$ \begin{align} {\sum_{\substack{j_1,j_2=1\\ j_1\neq j_2}}^N\int_{\mathbb{S}^{d-1}}g(\boldsymbol{\alpha},\boldsymbol{\alpha})\chi_{[0,\sigma_1]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_1},\boldsymbol{\alpha}))\chi_{[0,\sigma_2]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_2},\boldsymbol{\alpha}))\,d\boldsymbol{\alpha}} \end{align} $$
up to error
 $$ \begin{align} {<\epsilon\int_{\mathbb{S}^{d-1}}\sum_{\substack{j_1,j_2=1\\ j_1\neq j_2}}^N\chi_{[0,\sigma_1]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_1},\boldsymbol{\alpha}))\chi_{[0,\sigma_2]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_2},\boldsymbol{\alpha}))\,d\boldsymbol{\alpha}\ll\epsilon\sigma_1\sigma_2,} \end{align} $$
$$ \begin{align} {<\epsilon\int_{\mathbb{S}^{d-1}}\sum_{\substack{j_1,j_2=1\\ j_1\neq j_2}}^N\chi_{[0,\sigma_1]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_1},\boldsymbol{\alpha}))\chi_{[0,\sigma_2]}(N^{{1}/({d-1})}\mathbf{d}(\boldsymbol{\alpha}_{j_2},\boldsymbol{\alpha}))\,d\boldsymbol{\alpha}\ll\epsilon\sigma_1\sigma_2,} \end{align} $$
where the last inequality follows from Lemma 7.2 with the choice
![]() $h=1$
. Applying Lemma 7.2 again for equation (7.8) with the choice
$h=1$
. Applying Lemma 7.2 again for equation (7.8) with the choice
![]() $h(\boldsymbol {\alpha })=g(\boldsymbol {\alpha },\boldsymbol {\alpha })$
, we conclude the proof.
$h(\boldsymbol {\alpha })=g(\boldsymbol {\alpha },\boldsymbol {\alpha })$
, we conclude the proof.
Corollary 2.4 now follows from Lemma 7.3 by approximating
![]() ${f\kern1.3pt{\in}\kern1.3pt \operatorname {C}_0(\mathbb {S}^{d-1}\kern1.3pt{\times}\kern1.3pt \mathbb {S}^{d-1}\kern1.3pt{\times}\kern1.3pt \mathbb {R})}$
from above and below by finite linear combinations of functions of the form
${f\kern1.3pt{\in}\kern1.3pt \operatorname {C}_0(\mathbb {S}^{d-1}\kern1.3pt{\times}\kern1.3pt \mathbb {S}^{d-1}\kern1.3pt{\times}\kern1.3pt \mathbb {R})}$
from above and below by finite linear combinations of functions of the form
for suitable choices of
![]() $g\in \operatorname {C}(\mathbb {S}^{d-1}\times \mathbb {S}^{d-1})$
and
$g\in \operatorname {C}(\mathbb {S}^{d-1}\times \mathbb {S}^{d-1})$
and
![]() $\sigma _1,\sigma _2>0$
.
$\sigma _1,\sigma _2>0$
.
Acknowledgements
We thank João Lopes Dias, Andreas Strömbergsson and the anonymous referee for helpful comments. Research supported by EPSRC grant EP/S024948/1. W.K. is supported by the Korea Foundation for Advanced Studies (KFAS). No new data were generated or analysed during this study.
A Appendix. Brjuno-type condition
Following [Reference Lopes Dias and GaivãoLDG19] (cf. also [Reference Bounemoura and FéjozBF19]), we say that
![]() $\boldsymbol {\xi }\in \mathbb {R}^{d}$
is a s-Brjuno vector if
$\boldsymbol {\xi }\in \mathbb {R}^{d}$
is a s-Brjuno vector if
 $$ \begin{align*} {\sum_{n=0}^{\infty}2^{-{n}/{s}}\max_{\substack{\mathbf{m}\in\mathbb{Z}^d\setminus\{0\}\\ 0<|\mathbf{m}|\leq 2^{n}}}\log\frac{1}{|\boldsymbol{\xi}\cdot\mathbf{m}|_{\mathbb{Z}}}<\infty.} \end{align*} $$
$$ \begin{align*} {\sum_{n=0}^{\infty}2^{-{n}/{s}}\max_{\substack{\mathbf{m}\in\mathbb{Z}^d\setminus\{0\}\\ 0<|\mathbf{m}|\leq 2^{n}}}\log\frac{1}{|\boldsymbol{\xi}\cdot\mathbf{m}|_{\mathbb{Z}}}<\infty.} \end{align*} $$
The classical Brjuno condition corresponds to
![]() $s=1$
.
$s=1$
.
In this section, we prove that for
![]() $s>({\rho +1})/{\nu }$
, every s-Brjuno vector is
$s>({\rho +1})/{\nu }$
, every s-Brjuno vector is
![]() $(\rho ,0,\nu )$
- vaguely Diophantine. Given
$(\rho ,0,\nu )$
- vaguely Diophantine. Given
![]() $\boldsymbol {\xi }\in \mathbb {R}^{d}$
, let us define
$\boldsymbol {\xi }\in \mathbb {R}^{d}$
, let us define
![]() $\phi :\mathbb {N}\to \mathbb {R}^{>0}$
by
$\phi :\mathbb {N}\to \mathbb {R}^{>0}$
by
 $$ \begin{align*} {\phi(N):=\max_{\substack{\mathbf{m}\in\mathbb{Z}^d\setminus\{0\}\\ 0<|\mathbf{m}|\leq N}}\log\frac{1}{|\boldsymbol{\xi}\cdot\mathbf{m}|_{\mathbb{Z}}}.} \end{align*} $$
$$ \begin{align*} {\phi(N):=\max_{\substack{\mathbf{m}\in\mathbb{Z}^d\setminus\{0\}\\ 0<|\mathbf{m}|\leq N}}\log\frac{1}{|\boldsymbol{\xi}\cdot\mathbf{m}|_{\mathbb{Z}}}.} \end{align*} $$
Then the definition of
![]() $\zeta (\boldsymbol {\xi },T)$
can be written in terms of
$\zeta (\boldsymbol {\xi },T)$
can be written in terms of
![]() $\phi (N)$
as follows:
$\phi (N)$
as follows:
 $$ \begin{align*} {\begin{aligned}\zeta(\boldsymbol{\xi},T)&=\min\{N\in\mathbb{N}: e^{-\phi(N)}\leq T^{-1}\}\\&=\min\{N\in\mathbb{N}: \phi(N)\ge\log T\}.\end{aligned}} \end{align*} $$
$$ \begin{align*} {\begin{aligned}\zeta(\boldsymbol{\xi},T)&=\min\{N\in\mathbb{N}: e^{-\phi(N)}\leq T^{-1}\}\\&=\min\{N\in\mathbb{N}: \phi(N)\ge\log T\}.\end{aligned}} \end{align*} $$
Suppose that
![]() $\boldsymbol {\xi }$
is s-Brjuno type for some
$\boldsymbol {\xi }$
is s-Brjuno type for some
![]() $s>({\rho +1})/{\nu }$
. Then we have
$s>({\rho +1})/{\nu }$
. Then we have
![]() ${\sum _{n}2^{-{n}/{s}} \phi (2^{n})<\infty} $
, and hence
${\sum _{n}2^{-{n}/{s}} \phi (2^{n})<\infty} $
, and hence
![]() $\phi (t)\leq t^{{1}/{s}}\log 2$
for sufficiently large t. It follows that
$\phi (t)\leq t^{{1}/{s}}\log 2$
for sufficiently large t. It follows that
for sufficiently large l. Thus, it implies that
![]() $\boldsymbol {\xi }$
is
$\boldsymbol {\xi }$
is
![]() $(\rho ,0,\nu )$
-vaguely Diophantine since
$(\rho ,0,\nu )$
-vaguely Diophantine since
 $$ \begin{align*} {\sum_{l=1}^{\infty}l^\rho\, \zeta(\boldsymbol{\xi},2^{l-1})^{-\nu}\ll \sum_{l=1}^{\infty}l^{\rho-s\nu}<\infty.} \end{align*} $$
$$ \begin{align*} {\sum_{l=1}^{\infty}l^\rho\, \zeta(\boldsymbol{\xi},2^{l-1})^{-\nu}\ll \sum_{l=1}^{\infty}l^{\rho-s\nu}<\infty.} \end{align*} $$
B Appendix. Counterexamples
The following theorem establishes that for
![]() $d=2$
, there exist uncountably many
$d=2$
, there exist uncountably many
![]() ${\boldsymbol {\xi }\in \mathbb {R}^2\setminus \mathbb {Q}^2}$
such that the pair correlation function of the directions of the affine lattice
${\boldsymbol {\xi }\in \mathbb {R}^2\setminus \mathbb {Q}^2}$
such that the pair correlation function of the directions of the affine lattice
![]() $\mathbb {Z}^2+\boldsymbol {\xi }$
diverges, whilst converging to the Poisson limit along a subsequence.
$\mathbb {Z}^2+\boldsymbol {\xi }$
diverges, whilst converging to the Poisson limit along a subsequence.
Theorem B.1. Fix
![]() $s>0$
. Then there exists a set
$s>0$
. Then there exists a set
![]() ${\mathcal C}\subset \mathbb {R}^2$
of second Baire category with the property that for
${\mathcal C}\subset \mathbb {R}^2$
of second Baire category with the property that for
![]() $\boldsymbol {\xi }\in {\mathcal C}$
, there are sequences
$\boldsymbol {\xi }\in {\mathcal C}$
, there are sequences
![]() $(M_j)_{j\in \mathbb {N}}$
,
$(M_j)_{j\in \mathbb {N}}$
,
![]() $(N_j)_{j\in \mathbb {N}}$
with
$(N_j)_{j\in \mathbb {N}}$
with
![]() $M_j,N_j\to \infty $
such that
$M_j,N_j\to \infty $
such that
 $$ \begin{align} R^2_{M_j}(s) \geq \frac{\log M_j}{\log\log\log M_j} \end{align} $$
$$ \begin{align} R^2_{M_j}(s) \geq \frac{\log M_j}{\log\log\log M_j} \end{align} $$
and
 $$ \begin{align} \lim_{j\to \infty }R^2_{N_j}(s)=\frac{\pi^{({d-1})/{2}} s^{d-1}}{\Gamma(({d+1})/{2})}. \end{align} $$
$$ \begin{align} \lim_{j\to \infty }R^2_{N_j}(s)=\frac{\pi^{({d-1})/{2}} s^{d-1}}{\Gamma(({d+1})/{2})}. \end{align} $$
The proof of this statement follows from Theorem 1.1 and the next lemma by a Baire category argument identical to that used in [Reference SarnakSa97]; see also [Reference MarklofM03, §9].
Lemma B.2. Let
![]() $\boldsymbol {\xi }\in \mathbb {Q}^2$
. Then there exists a constant
$\boldsymbol {\xi }\in \mathbb {Q}^2$
. Then there exists a constant
![]() $C_{\boldsymbol {\xi }}$
such that for any
$C_{\boldsymbol {\xi }}$
such that for any
![]() $s>0$
and
$s>0$
and
![]() $T>0$
, we have
$T>0$
, we have
Proof. We first observe that for any
![]() $s>0$
and
$s>0$
and
![]() $N\in \mathbb {N}$
,
$N\in \mathbb {N}$
,
Let us first consider the case
![]() $\boldsymbol {\xi }=(0,0)$
. We denote the set of primitive lattice points by
$\boldsymbol {\xi }=(0,0)$
. We denote the set of primitive lattice points by
![]() $\mathbb {Z}^2_{\operatorname {prim}}$
. Then
$\mathbb {Z}^2_{\operatorname {prim}}$
. Then
 $$ \begin{align*} R^2_{N_0(T)}(s) &\geq \frac{1}{N_0(T)} \sum_{\mathbf{v}\in\mathbb{Z}^2_{\operatorname{prim}}}\sum_{\substack{k,l\neq0,\; k\neq l,\\\|k\mathbf{v}\|,\|l\mathbf{v}\|\leq T}}1 \\&\gg \frac{1}{T^2}\sum_{\substack{0\leq m<n\leq {T}/{2},\\ \operatorname{gcd}(m,n)=1}}\bigg(\frac{T}{n}\bigg)\bigg(\frac{T}{n}-1\bigg) \\&\gg \sum_{1\leq n\leq {T}/{2}}\frac{\varphi(n)}{n^2} \gg \log T \gg \log N_0(T), \end{align*} $$
$$ \begin{align*} R^2_{N_0(T)}(s) &\geq \frac{1}{N_0(T)} \sum_{\mathbf{v}\in\mathbb{Z}^2_{\operatorname{prim}}}\sum_{\substack{k,l\neq0,\; k\neq l,\\\|k\mathbf{v}\|,\|l\mathbf{v}\|\leq T}}1 \\&\gg \frac{1}{T^2}\sum_{\substack{0\leq m<n\leq {T}/{2},\\ \operatorname{gcd}(m,n)=1}}\bigg(\frac{T}{n}\bigg)\bigg(\frac{T}{n}-1\bigg) \\&\gg \sum_{1\leq n\leq {T}/{2}}\frac{\varphi(n)}{n^2} \gg \log T \gg \log N_0(T), \end{align*} $$
where
![]() $\varphi $
denotes Euler’s totient function. The above lower bound for the sum over the totient functions follows (via diadic decomposition) from the classic asymptotics
$\varphi $
denotes Euler’s totient function. The above lower bound for the sum over the totient functions follows (via diadic decomposition) from the classic asymptotics
![]() $\sum _{1\leq n\leq x} \varphi (n) \sim ({3}/{\pi ^2}) x^2$
.
$\sum _{1\leq n\leq x} \varphi (n) \sim ({3}/{\pi ^2}) x^2$
.
The case
![]() $\boldsymbol {\xi }\in \mathbb {Q}^2\setminus \{0\}$
is similar to the above. Let
$\boldsymbol {\xi }\in \mathbb {Q}^2\setminus \{0\}$
is similar to the above. Let
![]() $\boldsymbol {\xi }=({1}/{q})\mathbf {p}$
for some
$\boldsymbol {\xi }=({1}/{q})\mathbf {p}$
for some
![]() $\mathbf {p}=(p_1,p_2)\in \mathbb {Z}^2\setminus \{0\}$
and
$\mathbf {p}=(p_1,p_2)\in \mathbb {Z}^2\setminus \{0\}$
and
![]() $q\in \mathbb {N}$
. Then we have
$q\in \mathbb {N}$
. Then we have
 $$ \begin{align*} R^2_{N_0(T)}(s) &\geq \frac{1}{N_0(T)} \sum_{\mathbf{v}\in\mathbb{Z}^2_{\operatorname{prim}}}\sum_{\substack{k,l\neq 0,\;k\neq l,\\ \|k\mathbf{v}\|\leq qT,\; k\mathbf{v}\equiv \mathbf{p}\; (\operatorname{mod} q),\\ \|l\mathbf{v}\|\leq qT,\;l\mathbf{v}\equiv \mathbf{p}\; (\operatorname{mod} q)}}1 \\&\gg \frac{1}{T^2}\sum_{\substack{0\leq m<n\leq {T}/{2q},\\ \operatorname{gcd}(m,n)=1}}\bigg(\frac{T}{n}\bigg)\bigg(\frac{T}{n}-1\bigg)\\&\gg \sum_{1\leq n\leq {T}/{2q}}\frac{\varphi(n)}{n^2} \gg \log T \gg \log N_0(T). \end{align*} $$
$$ \begin{align*} R^2_{N_0(T)}(s) &\geq \frac{1}{N_0(T)} \sum_{\mathbf{v}\in\mathbb{Z}^2_{\operatorname{prim}}}\sum_{\substack{k,l\neq 0,\;k\neq l,\\ \|k\mathbf{v}\|\leq qT,\; k\mathbf{v}\equiv \mathbf{p}\; (\operatorname{mod} q),\\ \|l\mathbf{v}\|\leq qT,\;l\mathbf{v}\equiv \mathbf{p}\; (\operatorname{mod} q)}}1 \\&\gg \frac{1}{T^2}\sum_{\substack{0\leq m<n\leq {T}/{2q},\\ \operatorname{gcd}(m,n)=1}}\bigg(\frac{T}{n}\bigg)\bigg(\frac{T}{n}-1\bigg)\\&\gg \sum_{1\leq n\leq {T}/{2q}}\frac{\varphi(n)}{n^2} \gg \log T \gg \log N_0(T). \end{align*} $$
This completes the proof of the lemma.