Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T04:11:41.856Z Has data issue: false hasContentIssue false
  • English
  • Français

Pointwise multiple averages for systems with two commuting transformations

Published online by Cambridge University Press:  14 March 2017

SEBASTIÁN DONOSO  and
WENBO SUN Open the ORCID record for WENBO SUN [Opens in a new window]
SEBASTIÁN DONOSO
Affiliation:
Center for Mathematical Modeling, University of Chile, Beauchef 851, Santiago, Chile email [email protected]
WENBO SUN
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road Evanston, IL 60208-2730, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for every ergodic measure-preserving system 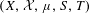$(X,{\mathcal{X}},\unicode[STIX]{x1D707},S,T)$ with commuting transformations $S$ and $T$, the average

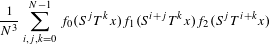$$\begin{eqnarray}\frac{1}{N^{3}}\mathop{\sum }_{i,j,k=0}^{N-1}f_{0}(S^{j}T^{k}x)f_{1}(S^{i+j}T^{k}x)f_{2}(S^{j}T^{i+k}x)\end{eqnarray}$$
converges for $\unicode[STIX]{x1D707}$-almost every 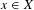$x\in X$ as 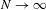$N\rightarrow \infty$ for all 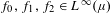$f_{0},f_{1},f_{2}\in L^{\infty }(\unicode[STIX]{x1D707})$. We also show that if 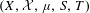$(X,{\mathcal{X}},\unicode[STIX]{x1D707},S,T)$ is an ergodic measurable distal system, then the average
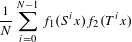$$\begin{eqnarray}\frac{1}{N}\mathop{\sum }_{i=0}^{N-1}f_{1}(S^{i}x)f_{2}(T^{i}x)\end{eqnarray}$$
 converges for $\unicode[STIX]{x1D707}$-almost every 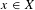$x\in X$ as 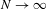$N\rightarrow \infty$ for all 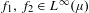$f_{1},f_{2}\in L^{\infty }(\unicode[STIX]{x1D707})$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 6 , September 2018 , pp. 2132 - 2157
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Austin, T.. On the norm convergence of non-conventional ergodic averages. Ergod. Th. & Dynam. Sys. 30(2) (2010), 321–338.Google Scholar
Becker, H. and Kechris, A.. The Descriptive Set Theory of Polish Group Actions (London Mathematical Society Lecture Note Series, 232) . Cambridge University Press, Cambridge, 1996.Google Scholar
Bourgain, J.. Double recurrence and almost sure convergence. J. Reine Angew. Math. 404 (1990), 140–161.Google Scholar
Chu, Q.. Multiple recurrence for two commuting transformations. Ergod. Th. & Dynam. Sys. 31(3) (2011), 771–792.Google Scholar
Donoso, S. and Sun, W.. A pointwise cubic average for two commuting transformations. Israel J. Math 216(2) (2016), 657–678.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (M. B. Porter Lectures) . Princeton University Press, Princeton, NJ, 1981.Google Scholar
Glasner, E.. Ergodic theory via joinings. (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Host, B.. Ergodic seminorms for commuting transformations and applications. Studia Math. 195(1) (2009), 31–49.Google Scholar
Host, B. and Kra, B.. Nonconventional averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 398–488.Google Scholar
Huang, W., Shao, S. and Ye, X. D.. Pointwise convergence of multiple ergodic averages and strictly ergodic models. Preprint, 2014, arXiv:1406.5930.Google Scholar
Jewett, R. I.. The prevalence of uniquely ergodic systems. J. Math. Mech. 19 (1969/1970), 717–729.Google Scholar
Krieger, W.. On unique ergodicity. Proc. Sixth Berkeley Symp. on Mathematical Statistics and Probability (University of California, Berkeley, CA, 1970/1971), Vol. II: Probability Theory. University of California Press, Berkeley, CA, 1972, pp. 327–346.Google Scholar
Tao, T.. Norm convergence of multiple ergodic averages for commuting transformations. Ergod. Th. & Dynam. Sys. 28(2) (2008), 657–688.Google Scholar
Walsh, M.. Norm convergence of nilpotent ergodic averages. Ann. of Math. (2) 175(3) (2012), 1667–1688.Google Scholar
Weiss, B.. Strictly ergodic models for dynamical systems. Bull. Amer. Math. Soc. (N. S.) 13 (1985), 143–146.Google Scholar