Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-05T02:40:47.907Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Cr-closing lemma for flows on the torus T2

Published online by Cambridge University Press:  19 September 2008

C. Gutierrez
C. Gutierrez
Affiliation:
Instituto de Matemática Pura e Aplicada, Estrada Dona Castorina, 110, Jardim Botânico, Rio de Janeiro, RJ CEP 22.460, Brazil
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

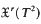Vector fields of , 1 ≤ r ≤ ∞, with non-trivial recurrent points are classified in two types, one of which we call the constant type inspired by the terminology of continued fractions. Let 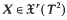have finitely many singularities and p ∈ T2 be a non-wandering point of X. With the exception of the case when X is of constant type and, simultaneously, p is non-trivial recurrent, we prove that there exists 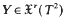arbitrarily close to X (in the Cr-topology) having a periodic trajectory through p.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 6 , Issue 1 , March 1986 , pp. 45 - 56
Copyright
Copyright © Cambridge University Press 1986

References

REFERENCES

[B—S]Bhatia, N. P. & Szego, B. P.. Stability Theory of Dynamical Systems. Springer-Verlag: New York (1970).CrossRefGoogle Scholar
[Gu.1]Gutierrez, C.. Smoothing continuous flows on two-manifolds and recurrences. Ergod. Th. & Dynam. Sys. 6 (1986), 17–44.CrossRefGoogle Scholar
[Gu.2]Gutierrez, C.. Structural stability for flows on the torus with a cross-cap. Trans. Amer. Math. Soc. 241 (1978), 311–320.CrossRefGoogle Scholar
[Her]Herman, M.. Sur la conjugaison différentiable des difféomorphismes du cercle a des rotations. Publ. Math. 49, 5–234.CrossRefGoogle Scholar
[Khi]Khintchine, A.. Kettenbrüche, B. G., Teubner Verlagsgesellschaft, Leipzig, 1956.Google Scholar
[La]Lang, S.. Introduction to Diophantine Approximations. Addison-Wesley Publishing Company, 1966.Google Scholar
[Ma]Mañé, R.. An ergodic closing lemma. Ann. of Math. 116 (1982), 503–541.CrossRefGoogle Scholar
[Ne]Neumann, D.. Smoothing continuous flows on 2-manifolds. Jour. Diff. Eq. 28, No. 3 (1978), 327–344.CrossRefGoogle Scholar
[Pa—Me]Palis, J. & de Melo, W.. Geometric Theory of Dynamical Systems. Springer-Verlag: New York (1982).CrossRefGoogle Scholar
[Pe]Peixoto, M.. Structural stability on two-dimensional manifolds. Topology 1 (1962), 101–120.CrossRefGoogle Scholar
[Px]Pixton, D.. Planar homoclinic points. J. Diff. Eq. 44 (1982), No. 3, 365–382.CrossRefGoogle Scholar
[Pg.1]Pugh, C.. Against the C2 closing lemma. Jour. Diff. Eq. 17 (1975), 435–443.CrossRefGoogle Scholar
[Pg.2]Pugh, C.. An improved closing lemma and general density theorem. Amer. J. Math. 89 (1967), 1010–1021.CrossRefGoogle Scholar
[SI]Slater, N. B.. Gaps and steps for the sequence nθ mod 1, Proc. Camb. Phil. Soc. 63 (1967), 1115–1123.CrossRefGoogle Scholar
[S—T]Schwartz, A. J. & Thomas, E. S.. The depth of the center of 2-manifolds. In Global Anal. Proc. Symp. Pure Math. 14, Amer. Math. Soc.: Providence, R.I., pp. 253–264 (1970).Google Scholar
[Ta]Takens, F.. Homoclinic points in conservative systems. Invent. Math. 18 (1972), 267–292.CrossRefGoogle Scholar
[Wa]Walters, P.. Ergodic Theory – Introductory Lectures. Springer-Verlag, 1975.CrossRefGoogle Scholar
[Wt]Whitney, H.. Regular families of curves. Ann. of Math. (2), 34 (1933), 244–270.CrossRefGoogle Scholar