Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T10:12:57.331Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-rigidity for circle homeomorphisms with several break points

Published online by Cambridge University Press:  28 November 2017

ABDELHAMID ADOUANI  and
HABIB MARZOUGUI
ABDELHAMID ADOUANI
Affiliation:
University of Carthage, Faculty of Science of Bizerte, Department of Mathematics, Jarzouna, 7021, Tunisia email [email protected], [email protected], [email protected]
HABIB MARZOUGUI
Affiliation:
University of Carthage, Faculty of Science of Bizerte, Department of Mathematics, Jarzouna, 7021, Tunisia email [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we consider two class $P$-homeomorphisms, 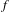$f$ and $g$, of the circle with break point singularities, that are differentiable maps except at some singular points where the derivative has a jump. Assume that they have the same irrational rotation number of bounded type and that the derivatives 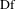$\text{Df}$ and 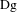$\text{Dg}$ are absolutely continuous on every continuity interval of 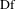$\text{Df}$ and 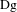$\text{Dg}$, respectively. We show that if 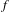$f$ and $g$ are not break-equivalent, then any topological conjugating 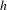$h$ between 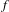$f$ and $g$ is a singular function, i.e., it is continuous on the circle, but $\text{Dh}(x)=0$ almost everywhere (a.e.) with respect to the Lebesgue measure. In particular, this result holds under some combinatorial assumptions on the jumps at break points. It also generalizes previous results obtained for one and two break points and complements that of Cunha–Smania which was established for break equivalence.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 9 , September 2019 , pp. 2305 - 2331
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adouani, A.. Conjugation between circle maps with several break points. Ergod. Th. & Dynam. Sys. 36 (2016), 2351–2383.Google Scholar
Adouani, A. and Marzougui, H.. Sur les Homéomorphismes du cercle de classe P C r par morceaux (r ≥ 1) qui sont conjugués C r par morceaux aux rotations irrationnelles. Ann. Inst. Fourier 58 (2008), 755–775.Google Scholar
Adouani, A. and Marzougui, H.. Singular measures for class P-circle homeomorphisms with several break points. Ergod. Th. & Dynam. Sys. 34 (2014), 423–456.Google Scholar
Adouani, A. and Marzougui, H.. A sharp smoothness of the conjugation of Class P-homeomorphisms to diffeomorphisms. Kodai Math J. 39 (2016), 425–438.Google Scholar
Akhadkulov, K. A.. Some circle homeomorphisms with break-type singularities. Russian Math. Surveys 61(5) (2006), 981–983.Google Scholar
Akhadkulov, H., Dzhalilov, A. and Mayer, D.. On conjugations of circle homeomorphisms with two break points. Ergod. Th. & Dynam. Sys. 34 (2014), 725–741.Google Scholar
Akhadkulov, H., Dzhalilov, A. and Noorani, M. S. M.. On conjugacies between piecewise-smooth circle maps. Nonlinear Anal. 99 (2014), 1–15.Google Scholar
Akhadkulov, H., Noorani, M. S. M. and Akhatkulov, S.. Notes on conjugacies and renormalizations of circle diffeomorphisms with breaks. J. Quality Measure. Anal. 10 (2014), 87–98.Google Scholar
Cunha, K. and Smania, D.. Rigidity for piecewise smooth homeomorphisms on the circle. Adv. Math. 250 (2014), 193–226.Google Scholar
de Melo, W. and van Strien, S.. One-dimensional Dynamics, Ergebnisse der Mathematik und ihrer Grenzgebiete. Vol. 25. Springer, Berlin, 1993.Google Scholar
Denjoy, A.. Sur les courbes définies par les équations differentielles à la surface du tore. J. Math. Pures Appl. (9) 11 (1932), 333–375.Google Scholar
Dzhalilov, A., Akin, H. and Temir, S.. Conjugations between circle maps with a single break point. J. Math. Anal. Appl. 366 (2010), 1–10.Google Scholar
Dzhalilov, A., Mayer, D. and Safarov, U.. On the conjugation of piecewise smooth circle homeomorphisms with a finite number of break points. Nonlinearity 28 (2015), 2441–2459.Google Scholar
Finzi, A.. Sur le problème de la génération d’une transformation donnée d’une courbe fermée par une transformation infinitésimale. Ann. Sci. Éc. Norm. Supér. (3) 67 (1950), 243–305.Google Scholar
Hasselblatt, B. and Katok, A.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.Google Scholar
Herman, M.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–234.Google Scholar
Hewitt, E. and Stromberg, K.. Real and Abstract Analysis (Graduate Text in Mathematics, 25) . Springer, Berlin, 1965.Google Scholar
Katznelson, Y. and Ornstein, D.. The differentiability of the conjugation of certain diffeomorphisms of the circle. Ergod. Th. & Dynam. Sys. 9 (1989), 643–680.Google Scholar
Khanin, K. M. and Khmelev, D.. Renormalizations and rigidity theory for circle homeomorphisms with singularities of the break type. Commun. Math. Phys. 235 (2003), 69–124.Google Scholar
Khanin, K. M. and Sinai, Y. G.. Smoothness of conjugacies of diffeomorphisms of the circle with rotations. Russian Math. Surveys 44 (1989), 69–99.Google Scholar
Khanin, K. M. and Teplinsky, A.. Herman’s theory revisited. Invent. Math. 178 (2009), 333–344.Google Scholar
Khanin, K. and Teplinsky, A.. Renormalization horseshoe and rigidity theory for circle diffeomorphisms with breaks. Commun. Math. Phys. 320 (2013), 347–377.Google Scholar
Navas, A.. Groups of Circle Diffeomorphisms (Chicago Lectures in Mathematics Series) . University of Chicago Press, Chicago, IL, 2011.Google Scholar
Poincaré, H.. Sur les courbes définies par les équations différentielles. J. Math. Pures Appl. (9) 1 (1885), 167–244.Google Scholar
Sinai, Y. G.. Topics in Ergodic Theory. Princeton University Press, Princeton, NJ, 1994.Google Scholar
Teplinsky, A.. A circle diffeomorphism with breaks that is smoothly linearizable. Ergod. Th. & Dynam. Sys., First published online 2016, page 1 of 13. doi:10.1017/etds.2016.24.Google Scholar
Yoccoz, J. C.. Il n’ y a pas de contre-exemple de Denjoy analytique. C. R. Math. Acad. Sci. Paris 298(serie I) (1984), 141–144.Google Scholar