Hostname: page-component-5f745c7db-96s6r Total loading time: 0 Render date: 2025-01-06T21:13:44.115Z Has data issue: true hasContentIssue false
  • English
  • Français

Monic representations of finite higher-rank graphs

Part of: Topological (rings and) algebras with an involution Selfadjoint operator algebras

Published online by Cambridge University Press:  06 September 2018

CARLA FARSI ,
ELIZABETH GILLASPY ,
PALLE JORGENSEN ,
SOORAN KANG  and
JUDITH PACKER
CARLA FARSI
Affiliation:
Department of Mathematics, University of Colorado at Boulder, Boulder, CO 80309-0395, USA email [email protected], [email protected]
ELIZABETH GILLASPY
Affiliation:
Department of Mathematics, University of Montana, 32 Campus Drive #0864, Missoula, MT 59812-0864, USA email [email protected]
PALLE JORGENSEN
Affiliation:
Department of Mathematics, 14 MLH, University of Iowa, Iowa City, IA 52242-1419, USA email [email protected]
SOORAN KANG
Affiliation:
College of General Education, Chung-Ang University, 84 Heukseok-ro, Dongjak-gu, Seoul, Republic of Korea email [email protected]
JUDITH PACKER
Affiliation:
Department of Mathematics, University of Colorado at Boulder, Boulder, CO 80309-0395, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we define the notion of monic representation for the 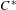$C^{\ast }$-algebras of finite higher-rank graphs with no sources, and we undertake a comprehensive study of them. Monic representations are the representations that, when restricted to the commutative 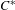$C^{\ast }$-algebra of the continuous functions on the infinite path space, admit a cyclic vector. We link monic representations to the 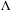$\unicode[STIX]{x1D6EC}$-semibranching representations previously studied by Farsi, Gillaspy, Kang and Packer (Separable representations, KMS states, and wavelets for higher-rank graphs. J. Math. Anal. Appl. 434 (2015), 241–270) and also provide a universal representation model for non-negative monic representations.

Keywords

monic representations𝛬-semibranching function systemsMarkov measuresprojective systems

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L55: Noncommutative dynamical systems 46K10: Representations of topological algebras with involution
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 5 , May 2020 , pp. 1238 - 1267
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alpay, D., Jorgensen, P. E. T. and Lewkowicz, I.. Markov measures, transfer operators, wavelets and multiresolutions. Frames and Harmonic Analysis (Contemporary Mathematics, 706). American Mathematical Society, Providence, RI, 2018, pp. 293–343.Google Scholar
Arveson, W.. An Invitation to C ∗ -Algebras (Graduate Texts in Mathematics, 39). Springer, New York, 1976.Google Scholar
Bezuglyi, S. and Jorgensen, P. E. T.. Representations of Cuntz–Krieger relations, dynamics on Bratteli diagrams, and path-space measures. Trends in Harmonic Analysis and its Applications (Contemporary Mathematics, 650). American Mathematical Society, Providence, RI, 2015, pp. 57–88.Google Scholar
Bezuglyi, S. and Jorgensen, P. E. T.. Infinite-dimensional Transfer Operators, Endomorphisms, and Measurable Partitions (Lecture Notes in Mathematics, 2217). Springer, Cham, 2018.Google Scholar
Bezuglyi, S., Kwiatkowski, J. and Medynets, K.. Aperiodic substitution systems and their Bratteli diagrams. Ergod. Th. & Dynam. Sys. 29 (2009), 37–72.Google Scholar
Bezuglyi, S., Kwiatkowski, J., Medynets, K. and Solomyak, B.. Finite rank Bratteli diagrams: structure of invariant measures. Trans. Amer. Math. Soc. 365 (2013), 2637–2679.Google Scholar
Bratteli, O. and Jorgensen, P. E. T.. Iterated function systems and permutation representations of the Cuntz algebra. Mem. Amer. Math. Soc. 139 (1999), x+89 pp.Google Scholar
Bratteli, O., Jorgensen, P. E. T. and Price, J.. Endomorphisms of 𝓑(𝓗). Quantization, Nonlinear Partial Differential Equations, and Operator Algebra (Proceedings of Symposia in Pure Mathematics, 59). American Mathematical Society, Providence, RI, 1994, pp. 93–138.Google Scholar
Carlsen, T. M., Kang, S., Shotwell, J. and Sims, A.. The primitive ideals of the Cuntz–Krieger algebra of a row-finite higher-rank graph with no sources. J. Funct. Anal. 266 (2014), 2570–2589.Google Scholar
Carlsen, T. M., Ruiz, E. and Sims, A.. Equivalence and stable isomorphism of groupoids, and diagonal-preserving stable isomorphisms of graph C ∗ -algebras and Leavitt path algebras. Proc. Amer. Math. Soc. 145 (2017), 1581–1592.Google Scholar
Cuntz, J.. Simple C ∗ -algebras generated by isometries. Comm. Math. Phys. 57 (1977), 173–185.Google Scholar
Cuntz, J. and Krieger, W.. A class of C ∗ -algebras and topological Markov chains. Invent. Math. 56 (1980), 251–268.Google Scholar
Davidson, K. R., Power, S. C. and Yang, D.. Atomic representations of rank 2 graph algebras. J. Funct. Anal. 255 (2008), 819–853.Google Scholar
Davidson, K. R. and Yang, D.. Representations of higher rank graph algebras. New York J. Math. 15 (2009), 169–198.Google Scholar
Dixmier, J.. Les C ∗ -algèbres et leurs représentations (Cahiers Scientifiques, Fasc. XXIX). Éditions Jacques Gabay, Paris, 1964.Google Scholar
Durrett, R.. Probability: Theory And Examples, 2nd edn. Cambridge University Press, Cambridge, MA, 1996, 440 pp.Google Scholar
Dutkay, D. E., Haussermann, J. and Jorgensen, P. E. T.. Atomic representations of Cuntz algebras. J. Math. Anal. Appl. 421 (2015), 215–243.Google Scholar
Dutkay, D. E. and Jorgensen, P. E. T.. Martingales, endomorphisms, and covariant systems of operators in Hilbert space. J. Operator Theory 58 (2007), 269–310.Google Scholar
Dutkay, D. E. and Jorgensen, P. E. T.. Fourier series on fractals: a parallel with wavelet theory. Radon Transforms, Geometry, and Wavelets (Contemporary Mathematics, 464). American Mathematical Society, Providence, RI, 2008, pp. 75–101.Google Scholar
Dutkay, D. E. and Jorgensen, P. E. T.. Monic representations of the Cuntz algebra and Markov measures. J. Funct. Anal. 267 (2014), 1011–1034.Google Scholar
Effros, E.. The Borel space of von Neumann algebras on a separable Hilbert space. Pacific J. Math. 15 (1965), 1153–1164.Google Scholar
Effros, E.. Transformation groups and C ∗ -algebras. Ann. of Math. (2) 81 (1965), 38–55.Google Scholar
Enomoto, M. and Watatani, Y.. A graph theory for C ∗ -algebras. Math. Japon. 25 (1980), 435–442.Google Scholar
Farsi, C., Gillaspy, E., Jorgensen, P. E. T., Kang, S. and Packer, J.. Representations of higher-rank graph C ∗ -algebras associated to 𝛬-semibranching function systems. J. Math. Anal. Appl., to appear.Google Scholar
+ Farsi, C., Gillaspy, E., Julien, A., Kang, S. and Packer, J.. Wavelets and Spectral Triples for Fractal Representations of Cuntz Algebras (Contemporary Mathematics, 687). American Mathematical Society, Providence, RI, 2017, pp. 103–133.Google Scholar
Farsi, C., Gillaspy, E., Julien, A., Kang, S. and Packer, J.. Spectral triples and wavelets for higher-rank graphs, Preprint, 2018, arXiv:1803.09304.Google Scholar
Farsi, C., Gillaspy, E., Kang, S. and Packer, J.. Separable representations, KMS states, and wavelets for higher-rank graphs. J. Math. Anal. Appl. 434 (2015), 241–270.Google Scholar
Farsi, C., Gillaspy, E., Kang, S. and Packer, J.. Wavelets and Graph C ∗ -algebras (Excursions in Harmonic Analysis, 5). Eds. Balan, R., Begué, M., Benedetto, J. J., Czaja, W. and Okoudjou, K. A.. Birkhäuser/Springer, Cham, 2017.Google Scholar
Glimm, J.. Locally compact transformation groups. Trans. Amer. Math. Soc. 101 (1961), 124–138.Google Scholar
Glimm, J.. Families of induced representations. Pacific J. Math. 12 (1962), 885–911.Google Scholar
Jones, V.. Von Neumann algebras in mathematics and physics. Introduction to Modern Mathematics (Advanced Lectures in Mathematics (ALM), 33). International Press, Somerville, MA, 2015, pp. 285–321.Google Scholar
Jorgensen, P. E. T.. Iterated function systems, representations, and Hilbert space. Internat. J. Math. 15(8) (2004), 813–832.Google Scholar
Kakutani, S.. On equivalence of infinite product measures. Ann. of Math. (2) 49 (1948), 214–224.Google Scholar
Kang, S. and Pask, D.. Aperiodicity and primitive ideals of row-finite k-graphs. Internat. J. Math. 25 (2014),1450022, 25 pp.Google Scholar
Kawamura, K.. Pure states on Cuntz algebras arising from geometric progressions. Algebr. Represent. Theory 19 (2016), 1297–1319.Google Scholar
Kolmogorov, A. N.. Foundations of the Theory of Probability. Chelsea Publishing Company, New York, 1950.Google Scholar
Kumjian, A. and Pask, D.. Higher-rank graph C ∗ -algebras. New York J. Math. 6 (2000), 1–20.Google Scholar
Kumjian, A., Pask, D. and Raeburn, I.. Cuntz–Krieger algebras of directed graphs. Pacific J. Math. 184 (1998), 161–174.Google Scholar
Laca, M.. Endomorphisms of 𝓑(𝓗) and Cuntz algebras. J. Operator Theory 30 (1993), 85–108.Google Scholar
Marcolli, M. and Paolucci, A. M.. Cuntz–Krieger algebras and wavelets on fractals. Complex Anal. Oper. Theory 5 (2011), 41–81.Google Scholar
Moore, C. C.. Group extensions and cohomology for locally compact groups. III. Trans. Amer. Math. Soc. 221 (1976), 1–33.Google Scholar
Nelson, E.. Topics in Dynamics. I: Flows. Math. Notes. Princeton University Press, Princeton, NJ, 1969.Google Scholar
Pask, D., Raeburn, I. and Weaver, N.. A family of 2-graphs arising from two-dimensional subshifts. Ergod. Th. & Dynam. Sys. 29 (2009), 1613–1639.Google Scholar
Pask, D., Sierakowski, A. and Sims, A.. Twisted k-graph algebras associated to Bratteli diagrams. Integr. Equ. Oper. Theory 81 (2015), 375–408.Google Scholar
Robertson, G. and Steger, T.. C ∗ -algebras arising from group actions on the boundary of a triangle building. Proc. Lond. Math. Soc. (3) 72 (1996), 613–637.Google Scholar
Robertson, G. and Steger, T.. Affine buildings, tiling systems and higher rank Cuntz–Krieger algebras. J. reine angew. Math. 513 (1999), 115–144.Google Scholar
Skalski, A. and Zacharias, J.. Entropy of shifts on higher-rank graph C ∗ -algebras. Houston J. Math. 34(1) (2008), 269–282.Google Scholar
Strichartz, R. S.. Besicovitch meets Wiener–Fourier expansions and fractal measures. Bull. Amer. Math. Soc. (N.S.) 20 (1989), 54–59.Google Scholar
Tumulka, R.. A Kolmogorov extension theorem for POVMs. Lett. Math. Phys. 84 (2008), 4–46.Google Scholar
Yang, D.. Endomorphisms and modular theory of 2-graph C ∗ -algebras. Indiana Univ. Math. J. 59 (2010), 495–520.Google Scholar