Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-06T04:06:01.215Z Has data issue: false hasContentIssue false
  • English
  • Français

Local structure of self-affine sets

Published online by Cambridge University Press:  06 September 2012

CHRISTOPH BANDT  and
ANTTI KÄENMÄKI
CHRISTOPH BANDT
Affiliation:
Institute for Mathematics and Informatics, Arndt University, 17487 Greifswald, Germany (email: [email protected])
ANTTI KÄENMÄKI
Affiliation:
Department of Mathematics and Statistics, PO Box 35 (MaD), FI-40014 University of Jyväskylä, Finland (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The structure of a self-similar set with the open set condition does not change under magnification. For self-affine sets, the situation is completely different. We consider self-affine Cantor sets 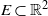$E\subset \mathbb {R}^2$ of the type studied by Bedford, McMullen, Gatzouras and Lalley, for which the projection onto the horizontal axis is an interval. We show that in small square $\varepsilon $-neighborhoods 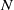$N$ of almost each point $x$ in 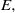$E,$ with respect to many Bernoulli measures on the address space, 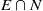$E\cap N$ is well approximated by product sets 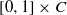$[0,1]\times C$, where 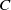$C$ is a Cantor set. Even though 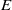$E$ is totally disconnected, all tangent sets have a product structure with interval fibers, reminiscent of the view of attractors of chaotic differentiable dynamical systems. We also prove that 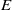$E$has uniformly scaling scenery in the sense of Furstenberg, Gavish and Hochman: the family of tangent sets is the same at almost all points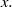$x.$

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 5 , October 2013 , pp. 1326 - 1337
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bandt, C.. Local geometry of fractals given by tangent measure distributions. Monatsh. Math. 133(4) (2001), 265–280.CrossRefGoogle Scholar
[2]Bandt, C. and Kravchenko, A.. Differentiability of fractal curves. Nonlinearity 24 (2011), 2717–2728.CrossRefGoogle Scholar
[3]Barnsley, M. F.. Fractals Everywhere, 2nd edn. Academic Press, New York, 1993.Google Scholar
[4]Bedford, T., Fisher, A. M. and Urbański, M.. The scenery flow for hyperbolic Julia sets. Proc. Lond. Math. Soc. 85(2) (2002), 467–492.Google Scholar
[5]Bedford, T.. Crinkly curves, Markov partitions and box dimension in self-similar sets. PhD Thesis, University of Warwick, 1984.Google Scholar
[6]Falconer, K. J.. Fractal Geometry. Wiley, New York, 1990.Google Scholar
[7]Furstenberg, H.. Ergodic fractal measures and dimension conservation. Ergod. Th. & Dynam. Sys. 28 (2008), 405–422.Google Scholar
[8]Gatzouras, D. and Lalley, S. P.. Hausdorff and box dimensions of certain self-affine fractals. Indiana Univ. Math. J. 41(2) (1992), 533–568.Google Scholar
[9]Gavish, M.. Measures with uniformly scaling scenery. Ergod. Th. & Dynam. Sys. 31 (2010), 33–48.Google Scholar
[10]Graf, S.. On Bandt’s tangential distribution for self-similar sets. Monatsh. Math. 120 (1995), 223–246.Google Scholar
[11]Graf, S., Mauldin, R. D. and Williams, S. C.. The exact Hausdorff dimension in random recursive constructions. Mem. Amer. Math. Soc. 381 (1988).Google Scholar
[12]Hochman, M.. Dynamics on fractal measures, arXiv 1008.3731.Google Scholar
[13]Käenmäki, A. and Vilppolainen, M.. Dimension and measures on sub-self-affine sets. Monatsh. Math. 161(3) (2010), 271–293.Google Scholar
[14]Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces. Cambridge University Press, Cambridge, 1995.Google Scholar
[15]McMullen, C. T.. The Hausdorff dimension of general Sierpiński carpets. Nagoya Math. J. 96(1) (1984), 1–9.Google Scholar
[16]Mörters, P. and Preiss, D.. Tangent measure distributions of fractal measures. Math. Ann. 312 (1998), 53–93.Google Scholar
[17]Peres, Y.. The self-affine carpets of McMullen and Bedford have infinite Hausdorff measure. Math. Proc. Cambridge Philos. Soc. 116 (1994), 513–526.Google Scholar
[18]Xiao, Y.. Random fractals and Markov processes. Fractal Geometry and Applications: A Jubilee of Benoit Mandelbrot. Eds. Lapidus, M. L. and van Frankenhuijsen, M.. American Mathematical Society, Providence, RI, 2004, pp. 261–338.CrossRefGoogle Scholar