Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-30T05:02:17.280Z Has data issue: false hasContentIssue false
  • English
  • Français

Leafwise quasigeodesic foliations in dimension three and the funnel property

Part of: Global differential geometry Differential topology Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  31 August 2022

ANINDYA CHANDA Open the ORCID record for ANINDYA CHANDA [Opens in a new window]  and
SÉRGIO R. FENLEY Open the ORCID record for SÉRGIO R. FENLEY [Opens in a new window]
ANINDYA CHANDA
Affiliation:
Department of Mathematics, Florida State University, Tallahassee, FL 32306, USA (e-mail: [email protected], [email protected])
SÉRGIO R. FENLEY*
Affiliation:
Department of Mathematics, Florida State University, Tallahassee, FL 32306, USA (e-mail: [email protected], [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct one-dimensional foliations which are subfoliations of two-dimensional foliations in 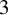$3$ -manifolds. The subfoliation is by quasigeodesics in each two-dimensional leaf, but it is not funnel: not all quasigeodesics share a common ideal point in most leaves.

Keywords

quasigeodesicssubfoliationsAnosov flows

MSC classification

Primary: 37C10: Vector fields, flows, ordinary differential equations 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.) 57R30: Foliations; geometric theory 53C23: Global geometric and topological methods (à la Gromov); differential geometric analysis on metric spaces
Secondary: 37D45: Strange attractors, chaotic dynamics 37C15: Topological and differentiable equivalence, conjugacy, invariants, moduli, classification 37D10: Invariant manifold theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 8 , August 2023 , pp. 2624 - 2650
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anosov, D. V.. Ergodic properties of geodesic flows on closed Riemannian manifolds of negative curvature. Dokl. Akad. Nauk SSSR 151 (1963), 1250−1252.Google Scholar
Anosov, D. V. and Sinaı, J. G.. Certain smooth ergodic systems. Uspekhi Mat. Nauk 22(5(137)) (1967), 107–172.Google Scholar
Béguin, F., Bonatti, C. and Yu, B.. Building Anosov flow on $3$ -manifolds. Geom. Topol. 21 (2017), 1837–1930.CrossRefGoogle Scholar
Barthelmé, T., Fenley, S. and Potrie, R.. Collapsed Anosov flows and self orbit equivalences. Preprint, 2022, arXiv:2008.0654. Comment. Math. Helv., to appear.Google Scholar
Burago, D. and Ivanov, S.. Partially hyperbolic diffeomorphisms of 3-manifolds with abelian fundamental groups . J. Mod. Dyn. 2(4) (2008), 541–580.CrossRefGoogle Scholar
Brunella, M.. Separating the basic sets of a nontransitive Anosov flow. Bull. Lond. Math. Soc. 25(5) (1993), 487–490.CrossRefGoogle Scholar
Calegari, D.. The geometry of R-covered foliations. Geom. Topol. 4 (2000), 457–515.CrossRefGoogle Scholar
Calegari, D.. Foliations and the Geometry of 3-Manifolds (Oxford Mathematical Monographs). Oxford University Press, Oxford, 2007.Google Scholar
Calegari, D.. Leafwise smoothing laminations. Algebr. Geom. Topol. 1 (2001), 579–585.CrossRefGoogle Scholar
Candel, A.. Uniformization of surface laminations. Ann. Sci. Éc. Norm. Supér. (4) 26(4) (1993), 489–516.CrossRefGoogle Scholar
Candel, A. and Conlon, L.. Foliations. I (Graduate Studies Mathematics, 23). American Mathematical Society, Providence, RI, 2000.Google Scholar
Fenley, S. R.. Anosov flows in 3-manifolds. Ann. of Math. (2) 139(1) (1994), 79–115.CrossRefGoogle Scholar
Fenley, S. R.. Foliations, topology and geometry of 3-manifolds: R-covered foliations and transverse pseudo-Anosov flows. Comment. Math. Helv. 77(3) (2002), 415–490.CrossRefGoogle Scholar
Fenley, S. and Mosher, L.. Quasigeodesic flows in hyperbolic 3-manifolds. Topology 40(3) (2001), 503–537.CrossRefGoogle Scholar
Franks, J. and Williams, B.. Anomalous Anosov flows. Global Theory of Dynamical Systems (Proceedings of an International Conference Held at Northwestern University, Evanston, Illinois, June 18-22, 1979) (Lecture Notes in Mathematics, 819). Springer, Berlin, 1980, pp. 158–174.Google Scholar
Gromov, M.. Hyperbolic groups. Essays in Group Theory (Mathematical Sciences Research Institute Publications, 8). Springer, New York, 1987, pp. 75–263.CrossRefGoogle Scholar
Inaba, T. and Matsumoto, S.. Nonsingular expansive flows on $3$ -manifolds and foliations with circle prong singularities. Jpn. J. Math. (N.S.) 16(2) (1990), 329–340.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and Its Applications, 54). Cambridge University Press, Cambridge, 1995. With a supplementary chapter by A. Katok and L. Mendoza.CrossRefGoogle Scholar
Paternain, M.. Expansive flows and the fundamental group. Bol. Soc. Brasil. Mat. (N.S.) 24(2) (1993), 179–199.CrossRefGoogle Scholar
Plante, J. F.. Foliations with measure preserving holonomy. Ann. of Math. (2) 102(2) (1975), 327–361.CrossRefGoogle Scholar
Shannon, M.. Dehn surgeries and smooth structures on 3-dimensional transitive Anosov flows. PhD Thesis, 2020, https://tel.archives-ouvertes.fr/tel-02951219/document.Google Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. (N.S.) 73 (1967), 747–817.CrossRefGoogle Scholar
Thurston, W. P.. Three-dimensional manifolds, Kleinian groups and hyperbolic geometry. Bull. Amer. Math. Soc. (N.S.) 6(3) (1982), 357–381.CrossRefGoogle Scholar
Thurston, W. P.. Three Dimensional Geometry and Topology (Princeton Mathematical Series, 35). Vol. 1. Princeton University Press, Princeton, NJ, 1997.CrossRefGoogle Scholar