Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-08T19:27:40.516Z Has data issue: false hasContentIssue false
  • English
  • Français

KMS states on the crossed product $C^*$-algebra of a homeomorphism

Part of: Selfadjoint operator algebras Ergodic theory

Published online by Cambridge University Press:  15 February 2021

JOHANNES CHRISTENSEN Open the ORCID record for JOHANNES CHRISTENSEN [Opens in a new window]  and
KLAUS THOMSEN
JOHANNES CHRISTENSEN*
Affiliation:
Department of Mathematics, Aarhus University, Ny Munkegade, 8000Aarhus C, Denmark (e-mail: [email protected])
KLAUS THOMSEN
Affiliation:
Department of Mathematics, Aarhus University, Ny Munkegade, 8000Aarhus C, Denmark (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

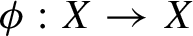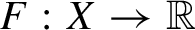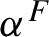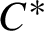Let $\phi :X\to X$ be a homeomorphism of a compact metric space X. For any continuous function $F:X\to \mathbb {R}$ there is a one-parameter group $\alpha ^{F}$ of automorphisms (or a flow) on the crossed product $C^*$ -algebra 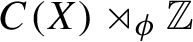$C(X)\rtimes _{\phi }\mathbb {Z}$ defined such that 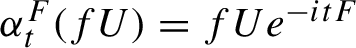$\alpha ^{F}_{t}(fU)=fUe^{-itF}$ when $f \in C(X)$ and U is the canonical unitary in the construction of the crossed product. In this paper we study the Kubo--Martin--Schwinger (KMS) states for these flows by developing an intimate relation to the ergodic theory of non-singular transformations and show that the structure of KMS states can be very rich and complicated. 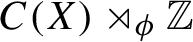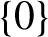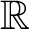Our results are complete concerning the set of possible inverse temperatures; in particular, we show that when $C(X) \rtimes _{\phi } \mathbb Z$ is simple this set is either $\{0\}$ or the whole line $\mathbb R$ .

Keywords

KMS statescrossed productsergodic theory

MSC classification

Primary: 46L30: States
Secondary: 37A55: Relations with the theory of $C^*$-algebras
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 4 , April 2022 , pp. 1373 - 1414
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athanassopoulos, K.. On the existence of absolutely continuous automorphic measures. Preprint, http://users.math.uoc.gr/~athanako/.Google Scholar
Baggett, L. W., Medina, H. A. and Merrill, K. D.. On functions that are trivial cocycles for a set of irrationals. II. Proc. Amer. Math. Soc. 124 (1996), 89–93.CrossRefGoogle Scholar
Bratteli, O. and Robinson, D. W.. Operator Algebras and Quantum Statistical Mechanics I + II (Texts and Monographs in Physics). Springer, New York, 1979 and 1981.CrossRefGoogle Scholar
Christensen, J.. Symmetries of the KMS simplex. Comm. Math. Phys. 364 (2018), 357–383.CrossRefGoogle Scholar
Christensen, J. and Thomsen, K.. Diagonality of actions and KMS weights. J. Operator Theory 76 (2016), 449–471.CrossRefGoogle Scholar
Denjoy, A.. Sur les courbes définies par des équations différentielles a la surface du tore. J. Math. Pures Appl. 9(11) (1932), 333–375.Google Scholar
de la Harpe, P. and Skandalis, G.. Déterminant associé à une trace sur une algébre de Banach. Ann. Inst. Fourier (Grenoble) 34(1) (1984), 169–202.Google Scholar
Denker, M. and Urbanski, M.. On the existence of conformal measures. Trans. Amer. Math. Soc. 328 (1991), 563–587.CrossRefGoogle Scholar
Douady, R. and Yoccoz, J.-C.. Nombre de rotation des difféomorphisms du cercles et mesures automorphes. Regul. Chaotic Dyn. 4 (1999), 3–24.CrossRefGoogle Scholar
Feldman, J. and Moore, C.. Ergodic equivalence relations, cohomology and von Neumann algebras. I. Trans. Amer. Math. Soc. 234(2) (1977), 289–324.CrossRefGoogle Scholar
Gottschalk, W. and Hedlund, G.. Topological Dynamics (American Mathematical Society Colloquium Publications, 36). American Mathematical Society, Providence, RI, 1955.CrossRefGoogle Scholar
Greschonig, G. and Schmidt, K.. Ergodic decomposition of quasi-invariant probability measures. Colloq. Math. 84/85 (2000), 495–514.CrossRefGoogle Scholar
Herman, M. R.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–233.CrossRefGoogle Scholar
Hochman, M.. A ratio ergodic theorem for multiparameter non-singular actions. J. Eur. Math. Soc. 12 (2010), 365–383.CrossRefGoogle Scholar
Katznelson, Y.. Sigma-finite invariant measures for smooth mappings of the circle. J. Anal. Math. 31 (1977), 1–18.CrossRefGoogle Scholar
Kadison, R. V. and Ringrose, J. R.. Fundamentals of the Theory of Operator Algebras II. Academic Press, Toronto, 1986.Google Scholar
Neshveyev, S.. KMS states on the ${C}^{\ast }$ -algebras of non-principal groupoids. J. Operator Theory 70 (2011), 513–530.CrossRefGoogle Scholar
Patterson, S. J.. The limit set of a Fuchsian group. Acta Math. 136 (1976), 241–273.CrossRefGoogle Scholar
Powers, R. T. and Sakai, S.. Existence of ground states and KMS states for approximately inner dynamics. Comm. Math. Phys. 39 (1975), 273–288.CrossRefGoogle Scholar
Sullivan, D.. Conformal dynamical systems. Geometric Dynamics (Lecture Notes in Mathematics, 1007). Springer, Berlin, 1983, pp. 725–752.CrossRefGoogle Scholar
Schmidt, K.. Unique ergodicity for quasi-invariant measures. Math. Z. 167 (1979), 169–172.CrossRefGoogle Scholar
Thomsen, K.. On the ${C}^{\ast }$ -algebra of a locally injective surjection and its KMS states. Comm. Math. Phys. 302 (2011), 403–423.CrossRefGoogle Scholar