Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-02T20:57:34.137Z Has data issue: false hasContentIssue false
  • English
  • Français

Immediate conditional hyperbolicity in dynamical systems

Published online by Cambridge University Press:  19 September 2008

Joseph Rosenblatt  and
Richard Swanson
Joseph Rosenblatt
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, Ohio 43210, USA
Richard Swanson
Affiliation:
Department of Mathematical Sciences, Montana State University, Bozeman, Montana 59717, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For many diffeomorphisms of a compact manifold X, eventual conditional hyperbolicity implies immediate conditional hyperbolicity in some (possibly new) Finsler structures. That is, if A and B are vector bundle isomorphisms over the mapping ƒ of the base X, such that 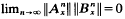uniformly on X, then there exist new norms for A and B such that 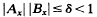uniformly on X, whenever the mapping ƒ satisfies the condition that there exist infinitely many N ≥ 1 such that any ƒ-invariant. For example, this condition on ƒ holds if any one of the following conditions holds: (1) ƒ is periodic; (2) ƒ is periodic on its non-wandering set; (3) ƒ has a finite non-wandering set (for example, ƒ is a Morse-Smale diffeomorphism); (4) ƒ is an almost periodic mapping of a connected base X; (5) ƒ is a mapping of the circle with no periodic points; or (6) ƒ and all its powers are uniquely ergodic. We consider various types of eventually conditionally hyperbolic systems and describe sufficient conditions on ƒ to have immediate conditional hyperbolicity of these systems in some new Finsler structures. Thus, for a sizable class of dynamical systems, we settle, in the affirmative, a question raised by Hirsch, Pugh, and Shub.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 3 , Issue 4 , December 1983 , pp. 627 - 647
Copyright
Copyright © Cambridge University Press 1983

References

REFERENCES

[1]Arnold, V. I. & Avez, A.. Ergodic Problems of Classical Mechanics. W. A. Benjamin, Inc: New York-Amsterdam, 1968.Google Scholar
[2]Chicone, C. & Swanson, R.. Spectral theory for linearizations of dynamical systems. J. Differential Equations 40 No. 2 (1981), 155–167.CrossRefGoogle Scholar
[3]del Junco, A. & Rosenblatt, J.. Counterexamples in ergodic theory and number theory. Math. Ann. 245 (1979), 185–197.CrossRefGoogle Scholar
[4]Derriennic, Y. & Krengel, U.. Subadditive mean ergodic theorems. Ergod. Th. & Dynam. Sys. 1 (1981), 9–32.CrossRefGoogle Scholar
[5]Furstenberg, H.. Strict ergodicity and transformations of the torus. Amer. J. Math. 83 (1961), 573–601.CrossRefGoogle Scholar
[6]Hirsch, M. W., Pugh, C. C. & Shub, M.. Invariant Manifolds. Lecture Notes in Math., No. 583. Springer-Verlag: Berlin-Heidelberg-New York, 1977.CrossRefGoogle Scholar
[7]Kingman, J. F. C.. Subadditive ergodic theory. Ann. Probab. 1 #6 (1973), 883–909.CrossRefGoogle Scholar
[8]Mañe, R.. Persistent manifolds are normally hyperbolic. Bull. Amer. Math. Soc. 80 (1974), 90–91.CrossRefGoogle Scholar
[9]Mather, J.. Characterization of Anosov diffeomorphisms. Indag. Math. 30 (1968), 479–483.CrossRefGoogle Scholar
[10]Nitecki, Z.. Differentiate Dynamics. M.I.T. Press: Cambridge, 1971.Google Scholar
[11]Oseledec, V. I.. A multiplicative ergodic theorem, Lyapunov characteristic numbers for a dynamical system. Trans. Moscow Math. Soc. 19 (1968), 197–231. (AMS, Providence, 1969.)Google Scholar