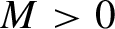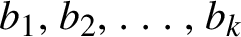1 Prime factors of binomial coefficients: Graham’s question
In the 1970s, Erdős, Graham, Ruzsa, and Straus proved that there are infinitely many integers n such that
 $\binom {2n}{n}$
is coprime with
$\binom {2n}{n}$
is coprime with
![]() $3\times 5=15,$
see [Reference Erdős, Graham, Ruzsa and Straus6]. Later on, Graham asked the following question.
$3\times 5=15,$
see [Reference Erdős, Graham, Ruzsa and Straus6]. Later on, Graham asked the following question.
Question 1.1. (Graham’s binomial coefficients problem)
Are there infinitely many integers
![]() $n\geq 1$
such that the binomial coefficient
$n\geq 1$
such that the binomial coefficient
 $\binom {2n}{n}$
is coprime with
$\binom {2n}{n}$
is coprime with
![]() $105=3\times 5\times 7?$
$105=3\times 5\times 7?$
Remark 1.2. According to [Reference Sloane16], Graham is offering $
![]() $1000$
to the first person with a solution.
$1000$
to the first person with a solution.
This problem turns out to be related to digit expansions of numbers in different bases. To be precise, let
![]() $b_{1},\ldots ,b_{k}\geq 2$
be
$b_{1},\ldots ,b_{k}\geq 2$
be
![]() $k\geq 2$
different integers. For each
$k\geq 2$
different integers. For each
![]() $i\in \{1,\ldots ,k\},$
let
$i\in \{1,\ldots ,k\},$
let
![]() $B_{i}\subset \{0,\ldots ,b_{i}-1\}$
be a subset of digits in base
$B_{i}\subset \{0,\ldots ,b_{i}-1\}$
be a subset of digits in base
![]() $b_{i}.$
Let
$b_{i}.$
Let
![]() $n,b\geq 2$
be integers, we write
$n,b\geq 2$
be integers, we write
![]() $D_{b}(n)$
for the set of digits used in representing n in base
$D_{b}(n)$
for the set of digits used in representing n in base
![]() $b.$
We define the set of integers
$b.$
We define the set of integers
 $$ \begin{align*} N_{b_{1},\ldots,b_{k}}^{B_{1},\ldots,B_{k}}=\{n\in\mathbb{N}: \text{ for all } i\in\{1,\ldots,k\}, D_{b_{i}}(n)\subset B_{i} \}. \end{align*} $$
$$ \begin{align*} N_{b_{1},\ldots,b_{k}}^{B_{1},\ldots,B_{k}}=\{n\in\mathbb{N}: \text{ for all } i\in\{1,\ldots,k\}, D_{b_{i}}(n)\subset B_{i} \}. \end{align*} $$
Thus,
 $N_{b_{1},\ldots ,b_{k}}^{B_{1},\ldots ,B_{k}}$
contains integers with very special digit expansions simultaneously in many different bases. We will call such numbers to be with restricted digits. The original motivation of this type of problem is to study prime factors of
$N_{b_{1},\ldots ,b_{k}}^{B_{1},\ldots ,B_{k}}$
contains integers with very special digit expansions simultaneously in many different bases. We will call such numbers to be with restricted digits. The original motivation of this type of problem is to study prime factors of
 $\binom {2n}{n}.$
The connection between prime factors of
$\binom {2n}{n}.$
The connection between prime factors of
 $\binom {2n}{n}$
and digit expansions of n was established by Kummer in [Reference Kummer13].
$\binom {2n}{n}$
and digit expansions of n was established by Kummer in [Reference Kummer13].
Theorem 1.3. (Kummer)
Let p be a prime number. Then
 $p \not | \binom {2n}{n}$
if and only if the p-ary expansion of n contains only digits
$p \not | \binom {2n}{n}$
if and only if the p-ary expansion of n contains only digits
![]() $\leq (p-1)/2.$
$\leq (p-1)/2.$
Due to Kummer’s theorem, we see that for Graham’s question, one needs to study the set
 $N_{3,5,7}^{B_{3},B_{5},B_{7}}$
, where
$N_{3,5,7}^{B_{3},B_{5},B_{7}}$
, where
It is precisely the set of integers n with
 $\binom {2n}{n}$
being coprime with
$\binom {2n}{n}$
being coprime with
![]() $3,5,7.$
Graham’s question is open, but there has been some progress. In [Reference Burrell and Yu4], it was proved that, under Schanuel’s conjecture (see Conjecture 3.1 below and [Reference Ax3]),
$3,5,7.$
Graham’s question is open, but there has been some progress. In [Reference Burrell and Yu4], it was proved that, under Schanuel’s conjecture (see Conjecture 3.1 below and [Reference Ax3]),
 $$ \begin{align*} \#N_{3,5,7}^{B_{3},B_{5},B_{7}}\cap [1,N]\leq N^{0.026} \end{align*} $$
$$ \begin{align*} \#N_{3,5,7}^{B_{3},B_{5},B_{7}}\cap [1,N]\leq N^{0.026} \end{align*} $$
for all sufficiently large N. So we can say that there are not ‘too many’ integers n such that
 $\binom {2n}{n}$
is coprime with
$\binom {2n}{n}$
is coprime with
![]() $3,5,7.$
Unconditionally, at least one of the results listed below holds for all large enough N:
$3,5,7.$
Unconditionally, at least one of the results listed below holds for all large enough N:
 $$ \begin{align*} \#N_{3,5,7}^{B_{3},B_{5},B_{7}}\cap [1,N]\leq N^{0.026}, \end{align*} $$
$$ \begin{align*} \#N_{3,5,7}^{B_{3},B_{5},B_{7}}\cap [1,N]\leq N^{0.026}, \end{align*} $$
 $$ \begin{align*} \#N_{3,5,11}^{B_{3},B_{5},B_{11}}\cap [1,N]\leq N^{0.061}, \end{align*} $$
$$ \begin{align*} \#N_{3,5,11}^{B_{3},B_{5},B_{11}}\cap [1,N]\leq N^{0.061}, \end{align*} $$
 $$ \begin{align*} \#N_{3,5,13}^{B_{3},B_{5},B_{13}}\cap [1,N]\leq N^{0.073}. \end{align*} $$
$$ \begin{align*} \#N_{3,5,13}^{B_{3},B_{5},B_{13}}\cap [1,N]\leq N^{0.073}. \end{align*} $$
The results in [Reference Burrell and Yu4] suggest a more quantitative conjecture as follows.
Conjecture 1.4. Let
![]() $p_{1},\ldots ,p_{k}$
be
$p_{1},\ldots ,p_{k}$
be
![]() $k\geq 2$
different odd prime numbers. For each
$k\geq 2$
different odd prime numbers. For each
![]() $i\in \{1,\ldots ,k\},$
let
$i\in \{1,\ldots ,k\},$
let
Consider the number
 $$ \begin{align*} s=\sum_{i=1}^{k} \frac{\log \#B_{i}}{\log p_{i}}=\sum_{i=1}^{k} \frac{\log (p_{i}+1)-\log 2}{\log p_{i}}. \end{align*} $$
$$ \begin{align*} s=\sum_{i=1}^{k} \frac{\log \#B_{i}}{\log p_{i}}=\sum_{i=1}^{k} \frac{\log (p_{i}+1)-\log 2}{\log p_{i}}. \end{align*} $$
If
![]() $s\in (k-1,k),$
then for each
$s\in (k-1,k),$
then for each
![]() $\epsilon>0$
, there is a constant
$\epsilon>0$
, there is a constant
![]() $C_{\epsilon }>1$
such that
$C_{\epsilon }>1$
such that
 $$ \begin{align} C^{-1}_{\epsilon} N^{s-(k-1)-\epsilon}\leq \# N_{p_{1},\ldots,p_{k}}^{B_{1},\ldots,B_{k}}\cap [1,N]\leq C_{\epsilon} N^{s-(k-1)+\epsilon} \end{align} $$
$$ \begin{align} C^{-1}_{\epsilon} N^{s-(k-1)-\epsilon}\leq \# N_{p_{1},\ldots,p_{k}}^{B_{1},\ldots,B_{k}}\cap [1,N]\leq C_{\epsilon} N^{s-(k-1)+\epsilon} \end{align} $$
for all integers
![]() $N\geq 2.$
If
$N\geq 2.$
If
![]() $s<k-1$
, then
$s<k-1$
, then
 $N_{p_{1},\ldots ,p_{k}}^{B_{1},\ldots ,B_{k}}$
is finite.
$N_{p_{1},\ldots ,p_{k}}^{B_{1},\ldots ,B_{k}}$
is finite.
Remark 1.5. The rightmost inequality of equation
![]() $(1)$
was proved in [Reference Burrell and Yu4] under Schanuel’s conjecture. Thus the open problem is the leftmost inequality of equation
$(1)$
was proved in [Reference Burrell and Yu4] under Schanuel’s conjecture. Thus the open problem is the leftmost inequality of equation
![]() $(1)$
and the finiteness statement. This is closely related to a Furstenberg’s problem, see [Reference Furstenberg8, Reference Shmerkin17, Reference Wu18].
$(1)$
and the finiteness statement. This is closely related to a Furstenberg’s problem, see [Reference Furstenberg8, Reference Shmerkin17, Reference Wu18].
2 Results in this paper
In this paper, we consider Graham’s question and other problems related to digit expansions of numbers in different bases. We relate it to projections of fractal sets, a well-studied topic in geometric measure theory. This connection does not directly provide us with new results. It merely represents some number-theoretic problems using fractals (self-similar sets) and translates the problems into geometric properties (intersections, slices, projections) of those fractals. We will provide a more detailed discussion on this topic in §§3 and 4. Here, we only need to know that
![]() $\Pi _{x}$
for
$\Pi _{x}$
for
![]() $x\in \mathbb {R}^{d}$
stands for the map
$x\in \mathbb {R}^{d}$
stands for the map
 $$ \begin{align*} y\in\mathbb{R}^{d}\setminus \{x\}\to \Pi_{x}(y)=\frac{x-y}{\lvert x-y\rvert}\in S^{d-1}. \end{align*} $$
$$ \begin{align*} y\in\mathbb{R}^{d}\setminus \{x\}\to \Pi_{x}(y)=\frac{x-y}{\lvert x-y\rvert}\in S^{d-1}. \end{align*} $$
Intuitively speaking, let
![]() $A\subset \mathbb {R}^{d}.$
Then
$A\subset \mathbb {R}^{d}.$
Then
![]() $\Pi _{x}(A)$
is what an observer can see of A at a certain position
$\Pi _{x}(A)$
is what an observer can see of A at a certain position
![]() $x\in \mathbb {R}^{d}.$
In what follows, we say that a list of numbers
$x\in \mathbb {R}^{d}.$
In what follows, we say that a list of numbers
![]() $a_{1},\ldots ,a_{d}$
are multiplicatively independent if they are not
$a_{1},\ldots ,a_{d}$
are multiplicatively independent if they are not
![]() $0$
or
$0$
or
![]() $1$
, and
$1$
, and
![]() $1,\log a_{2}/\log a_{1},\ldots ,\log a_{d}/\log a_{1}$
are linearly independent over the field of rational numbers. See §3.2 for the definition of self-similar sets and the open set condition. See [Reference Falconer7, Ch. 2] for the definition of the Hausdorff dimension (
$1,\log a_{2}/\log a_{1},\ldots ,\log a_{d}/\log a_{1}$
are linearly independent over the field of rational numbers. See §3.2 for the definition of self-similar sets and the open set condition. See [Reference Falconer7, Ch. 2] for the definition of the Hausdorff dimension (
![]() ${\dim _{\mathrm {H}}}$
).
${\dim _{\mathrm {H}}}$
).
Conjecture 2.1. Let
![]() $A\subset \mathbb {R}^{d},d\geq 2$
be a Cartesian product of self-similar sets in
$A\subset \mathbb {R}^{d},d\geq 2$
be a Cartesian product of self-similar sets in
![]() $\mathbb {R}$
with the open set condition and uniform contraction ratios. Suppose further that the contraction ratios are multiplicatively independent. If
$\mathbb {R}$
with the open set condition and uniform contraction ratios. Suppose further that the contraction ratios are multiplicatively independent. If
![]() ${\dim _{\mathrm {H}}} A>d-1,$
then
${\dim _{\mathrm {H}}} A>d-1,$
then
![]() $\Pi _{x}(A)$
has a non-empty interior for all
$\Pi _{x}(A)$
has a non-empty interior for all
![]() $x\in \mathbb {R}^{d}.$
$x\in \mathbb {R}^{d}.$
In §4, we will provide more details. Conjecture 2.1 turns out to be closely related to Graham’s question. We do not need the full strength of this conjecture. A special case will be enough. See Conjecture 4.2.
Theorem 2.2. Assuming Conjecture 2.1 and Schanuel’s conjecture, there are infinitely many integers n such that
 $\binom {2n}{n}$
is coprime with
$\binom {2n}{n}$
is coprime with
![]() $3\times 5\times 7.$
$3\times 5\times 7.$
Remark 2.3. We do not need the full strength of Schanuel’s conjecture. It is enough only to assume that
 $$ \begin{align*} 1,\frac{\log 3}{\log 5}, \frac{\log 3}{\log 7} \end{align*} $$
$$ \begin{align*} 1,\frac{\log 3}{\log 5}, \frac{\log 3}{\log 7} \end{align*} $$
are
![]() $\mathbb {Q}$
-linearly independent.
$\mathbb {Q}$
-linearly independent.
Currently, we are not able to prove Conjecture 2.1. Nonetheless, the strategy for proving Theorem 2.2 can be adapted to prove many other (unconditional) results concerning numbers with restricted digits.
First, we prove a quantitative version of a result in [Reference Erdős, Graham, Ruzsa and Straus6].
Theorem 2.4. Let
![]() $p,q$
be two different odd primes. Consider the set
$p,q$
be two different odd primes. Consider the set
 $$ \begin{align*} A=\bigg\{n\in\mathbb{N}: \mathrm{gcd}\bigg(pq,\binom{2n}{n}\bigg)=1\bigg\}. \end{align*} $$
$$ \begin{align*} A=\bigg\{n\in\mathbb{N}: \mathrm{gcd}\bigg(pq,\binom{2n}{n}\bigg)=1\bigg\}. \end{align*} $$
Then there is a constant
![]() $c>0$
depending on
$c>0$
depending on
![]() $p,q$
such that
$p,q$
such that
holds for all large enough integers N.
Next, we prove a result concerning linear forms of numbers with restricted digits.
Theorem 2.5. There are infinitely many integer triples
 $(x,y,z)\in N_{3}^{\{0,1\}}\times N_{4}^{\{0,1\}}\times N_{5}^{\{0,1\}}$
with
$(x,y,z)\in N_{3}^{\{0,1\}}\times N_{4}^{\{0,1\}}\times N_{5}^{\{0,1\}}$
with
Remark 2.6. This result says that there are infinitely many sums of powers of five that can be written as sums of powers of three and four. We list a few examples:
 $$ \begin{align*} 5&=4+1, \\ 5^{2}&=4^{2}+3^{2}, \\ 5^{3}+5^{2}&=3^{4}+4^{3}+4+1, \\ 5^{4}+5^{2}&=3^{5}+4^{4}+3^{4}+4^{3}+4+1+1. \end{align*} $$
$$ \begin{align*} 5&=4+1, \\ 5^{2}&=4^{2}+3^{2}, \\ 5^{3}+5^{2}&=3^{4}+4^{3}+4+1, \\ 5^{4}+5^{2}&=3^{5}+4^{4}+3^{4}+4^{3}+4+1+1. \end{align*} $$
It is perhaps possible that all large enough integers can be written as a sum of form
 $N^{\{0,1\}}_{3}+N^{\{0,1\}}_{4}.$
If so, this theorem would follow as a direct consequence. We believe that the conclusion does not hold for general triples
$N^{\{0,1\}}_{3}+N^{\{0,1\}}_{4}.$
If so, this theorem would follow as a direct consequence. We believe that the conclusion does not hold for general triples
![]() $(b_{1},b_{2},b_{3})$
in the place of
$(b_{1},b_{2},b_{3})$
in the place of
![]() $(3,4,5).$
For example, we suspect that there are only finitely many integer triples
$(3,4,5).$
For example, we suspect that there are only finitely many integer triples
 $(x,y,z)\in N_{9}^{\{0,1\}}\times N_{10}^{\{0,1\}}\times N_{11}^{\{0,1\}}$
with
$(x,y,z)\in N_{9}^{\{0,1\}}\times N_{10}^{\{0,1\}}\times N_{11}^{\{0,1\}}$
with
![]() $x+y=z.$
A partial result towards this direction is [Reference Yu20, Theorem 1.5] which says that for each
$x+y=z.$
A partial result towards this direction is [Reference Yu20, Theorem 1.5] which says that for each
![]() $\epsilon>0$
and large enough integer
$\epsilon>0$
and large enough integer
![]() $N,$
the amount of integer triples in
$N,$
the amount of integer triples in
![]() $[1,N]^{3}$
with the above property is
$[1,N]^{3}$
with the above property is
![]() $O(N^{\epsilon }).$
$O(N^{\epsilon }).$
Another very natural question to consider is whether there are infinite numbers with missing digits in many different bases at the same time. For example, are there integers
![]() $b_{1}>\cdots >b_{100}>2$
such that there are infinitely many integers whose base
$b_{1}>\cdots >b_{100}>2$
such that there are infinitely many integers whose base
![]() $b_{1},\ldots ,b_{100}$
expansions do not have digit zero? Our next result answers this question.
$b_{1},\ldots ,b_{100}$
expansions do not have digit zero? Our next result answers this question.
Theorem 2.7. Let
![]() $k\geq 2$
be an integer. Then there is an integer
$k\geq 2$
be an integer. Then there is an integer
![]() $M\geq 1$
such that for all k-tuples of multiplicative independent integers
$M\geq 1$
such that for all k-tuples of multiplicative independent integers
![]() $b_{1},\ldots ,b_{k}$
that are at least M, there are infinitely many integers whose base
$b_{1},\ldots ,b_{k}$
that are at least M, there are infinitely many integers whose base
![]() $b_{1},\ldots ,b_{k}$
expansions all omit the digit zero.
$b_{1},\ldots ,b_{k}$
expansions all omit the digit zero.
Remark 2.8. The missing digit zero is not a special choice. In fact, one can choose an integer
![]() $m\geq 1$
and consider digit expansions in different bases with an arbitrary choice of m missing digits for each base. Of course, this only makes sense if the bases in consideration are all greater than
$m\geq 1$
and consider digit expansions in different bases with an arbitrary choice of m missing digits for each base. Of course, this only makes sense if the bases in consideration are all greater than
![]() $m.$
$m.$
This brings us closer to Graham’s question. However, we are still far away. Kummer’s theorem indicates that for considering prime divisors of binomial coefficients, one needs to consider numbers that miss at least half of the digits in many different prime bases.
To prove the above results, we use Newhouse’s gap lemma. See §3.3. It is possible to prove Theorems 2.5, 2.7 without having the geometry of self-similar sets in mind. In fact, it is possible to prove those results by directly using arithmetic of integers and some well-known facts of irrational rotations just like the original arguments in [Reference Erdős, Graham, Ruzsa and Straus6, Lemma on p. 84]. For example, [Reference Erdős, Graham, Ruzsa and Straus6, Lemma on p. 84] can be viewed as an integer version of Newhouse’s gap lemma applied to ‘integer self-similar sets’. The point of using the fractal geometric point of view in this paper is to make the ideas behind the proofs more transparent. In fact, the core of the proof of Theorem 2.4 essentially uses the same ideas as in [Reference Erdős, Graham, Ruzsa and Straus6, Lemma on p. 84] but expresses them in a more geometric way.
3 Preliminaries
3.1 A remark for Schanuel’s conjecture
We need Schanuel’s conjecture because in some of the proofs, we will use properties of (irrational) rotations on a torus. Let
![]() $n\geq 1$
be an integer. Let
$n\geq 1$
be an integer. Let
![]() $\mathbb {T}^{n}=\mathbb {R}^{n}/\mathbb {Z}^{n}$
. Let
$\mathbb {T}^{n}=\mathbb {R}^{n}/\mathbb {Z}^{n}$
. Let
![]() $\alpha =(\alpha _{1},\ldots ,\alpha _{n})\in \mathbb {R}^{n}.$
We define the map
$\alpha =(\alpha _{1},\ldots ,\alpha _{n})\in \mathbb {R}^{n}.$
We define the map
![]() $T_{\alpha }:\mathbb {T}^{n}\to \mathbb {T}^{n}$
to be
$T_{\alpha }:\mathbb {T}^{n}\to \mathbb {T}^{n}$
to be
We say that
![]() $T_{\alpha }$
is the rotation on
$T_{\alpha }$
is the rotation on
![]() $\mathbb {T}^{n}$
with the rotation angle
$\mathbb {T}^{n}$
with the rotation angle
![]() $\alpha .$
If
$\alpha .$
If
![]() $1,\alpha _{1},\ldots ,\alpha _{n}$
are
$1,\alpha _{1},\ldots ,\alpha _{n}$
are
![]() $\mathbb {Q}$
-linearly independent, then we say that
$\mathbb {Q}$
-linearly independent, then we say that
![]() $T_{\alpha }$
is an irrational rotation. In this case, it is well known that for each
$T_{\alpha }$
is an irrational rotation. In this case, it is well known that for each
![]() $x\in \mathbb {T}^{n},$
$x\in \mathbb {T}^{n},$
 $$ \begin{align*} \overline{\{T^{k}_{\alpha}(x)\}_{k\geq 1}}=\mathbb{T}^{n}. \end{align*} $$
$$ \begin{align*} \overline{\{T^{k}_{\alpha}(x)\}_{k\geq 1}}=\mathbb{T}^{n}. \end{align*} $$
See [Reference Einsiedler and Ward5, Corollary 4.15].
Let
![]() $b_{1},b_{2}\ldots ,b_{n}$
be
$b_{1},b_{2}\ldots ,b_{n}$
be
![]() $n\geq 2$
integers. To study digit expansions with respect to these integers, it is often useful to consider the rotation on
$n\geq 2$
integers. To study digit expansions with respect to these integers, it is often useful to consider the rotation on
![]() $\mathbb {T}^{n-1}$
with the rotation angle,
$\mathbb {T}^{n-1}$
with the rotation angle,
To do this, it is useful to know whether the above vector generates an irrational rotation. This is the case if
 $$ \begin{align*} \Lambda^{\prime}=\bigg(\frac{\prod_{i=1}^{n} \log b_{i}}{\log b_{1}},\ldots, \frac{\prod_{i=1}^{n} \log b_{i}}{\log b_{n}}\bigg) \end{align*} $$
$$ \begin{align*} \Lambda^{\prime}=\bigg(\frac{\prod_{i=1}^{n} \log b_{i}}{\log b_{1}},\ldots, \frac{\prod_{i=1}^{n} \log b_{i}}{\log b_{n}}\bigg) \end{align*} $$
are
![]() $\mathbb {Q}$
-linearly independent. If
$\mathbb {Q}$
-linearly independent. If
![]() $n=2$
, then the situation is simple. For
$n=2$
, then the situation is simple. For
![]() $n\geq 3,$
the problem becomes challenging. For example, it is not known whether
$n\geq 3,$
the problem becomes challenging. For example, it is not known whether
![]() $1,\log 2/\log 3$
,
$1,\log 2/\log 3$
,
![]() $\log 2/\log 5$
are
$\log 2/\log 5$
are
![]() $\mathbb {Q}$
-linearly independent. Problems of this kind are related to Schanuel’s conjecture, see [Reference Ax3].
$\mathbb {Q}$
-linearly independent. Problems of this kind are related to Schanuel’s conjecture, see [Reference Ax3].
Conjecture 3.1. (Schanuel)
Let
![]() $n\geq 2$
be an integer. Let
$n\geq 2$
be an integer. Let
![]() $x_{1},\ldots ,x_{n}$
be
$x_{1},\ldots ,x_{n}$
be
![]() $\mathbb {Q}$
-linearly independent complex numbers. Then the transcendence degree of
$\mathbb {Q}$
-linearly independent complex numbers. Then the transcendence degree of
is at least n.
In the case when
![]() $e^{x_{1}},\ldots ,e^{x_{n}}$
are integers, the conjectures reduce to saying that
$e^{x_{1}},\ldots ,e^{x_{n}}$
are integers, the conjectures reduce to saying that
![]() $x_{1},\ldots ,x_{n}$
are algebraically independent over
$x_{1},\ldots ,x_{n}$
are algebraically independent over
![]() $\mathbb {Q}.$
This implies that
$\mathbb {Q}.$
This implies that
![]() $\Lambda ^{\prime }$
is indeed
$\Lambda ^{\prime }$
is indeed
![]() $\mathbb {Q}$
-linearly independent if
$\mathbb {Q}$
-linearly independent if
![]() $1,\log b_{1},\ldots ,\log b_{n}$
are
$1,\log b_{1},\ldots ,\log b_{n}$
are
![]() $\mathbb {Q}$
-linearly independent. This is the reason that whenever we are dealing with digit expansions with more than two bases, Schanuel’s conjecture is likely to appear. We are not using the full power of Schanuel’s conjecture here. However, this conjecture is so difficult that even the homogeneous quadratic case is not known. The only known result in this direction is Baker’s theory on linear forms of logarithms, see also [Reference Ax3] and the references therein for more details.
$\mathbb {Q}$
-linearly independent. This is the reason that whenever we are dealing with digit expansions with more than two bases, Schanuel’s conjecture is likely to appear. We are not using the full power of Schanuel’s conjecture here. However, this conjecture is so difficult that even the homogeneous quadratic case is not known. The only known result in this direction is Baker’s theory on linear forms of logarithms, see also [Reference Ax3] and the references therein for more details.
We should nonetheless remark that although we are dealing with digit expansions with more than two bases in this paper, the
![]() $\mathbb {Q}$
-linear independence of
$\mathbb {Q}$
-linear independence of
![]() $\Lambda ^{\prime }$
is not always involved. In fact, we will only need Schanuel’s conjecture for proving Theorem 2.2. For Theorem 2.5, the proof would be much simpler by assuming Schanuel’s conjecture. Additional efforts need to be taken to get rid of it. For Theorem 2.7, we simply do not meet the situation where Schanuel’s conjecture is needed.
$\Lambda ^{\prime }$
is not always involved. In fact, we will only need Schanuel’s conjecture for proving Theorem 2.2. For Theorem 2.5, the proof would be much simpler by assuming Schanuel’s conjecture. Additional efforts need to be taken to get rid of it. For Theorem 2.7, we simply do not meet the situation where Schanuel’s conjecture is needed.
3.2 Self-similar sets and the open set condition
Let
![]() $\mathcal {F}=\{f_{i}\}_{i\in \Lambda }$
be a finite collection of linear maps on
$\mathcal {F}=\{f_{i}\}_{i\in \Lambda }$
be a finite collection of linear maps on
![]() $\mathbb {R}.$
We can write down each linear map explicitly as
$\mathbb {R}.$
We can write down each linear map explicitly as
![]() $f_{i}(x)=r_{i}x+a_{i}.$
We assume that
$f_{i}(x)=r_{i}x+a_{i}.$
We assume that
![]() $r_{i}\in (0,1)$
for all
$r_{i}\in (0,1)$
for all
![]() $i\in \Lambda .$
We call such a collection of linear maps to be a linear iterated function system (IFS). The parameters
$i\in \Lambda .$
We call such a collection of linear maps to be a linear iterated function system (IFS). The parameters
![]() $r_{i},i\in \Lambda $
are called contraction ratios and
$r_{i},i\in \Lambda $
are called contraction ratios and
![]() $a_{i},i\in \Lambda $
are called translations. In the case when all the contraction ratios are equal to
$a_{i},i\in \Lambda $
are called translations. In the case when all the contraction ratios are equal to
![]() $r\in (0,1)$
, we call r to be the uniform contraction ratio.
$r\in (0,1)$
, we call r to be the uniform contraction ratio.
By [Reference Hutchinson11], there is a unique non-empty compact set F such that
 $$ \begin{align*} F=\bigcup_{i\in\Lambda} f_{i}(F). \end{align*} $$
$$ \begin{align*} F=\bigcup_{i\in\Lambda} f_{i}(F). \end{align*} $$
We call such a set F to be a self-similar set determined by
![]() $\mathcal {F}$
. We say that
$\mathcal {F}$
. We say that
![]() $\mathcal {F}$
satisfies the open set condition if there is a bounded open set
$\mathcal {F}$
satisfies the open set condition if there is a bounded open set
![]() $U\subset \mathbb {R}$
such that
$U\subset \mathbb {R}$
such that
![]() $f_{i}(U)\subset U$
for each
$f_{i}(U)\subset U$
for each
![]() $i\in \Lambda $
and
$i\in \Lambda $
and
as long as
![]() $i\neq j.$
The open set condition is a condition on
$i\neq j.$
The open set condition is a condition on
![]() $\mathcal {F}$
rather than
$\mathcal {F}$
rather than
![]() $F.$
However, we also say that F satisfies the open set condition if there is an IFS
$F.$
However, we also say that F satisfies the open set condition if there is an IFS
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $\mathcal {F}$
determines F and has the open set condition.
$\mathcal {F}$
determines F and has the open set condition.
Let
![]() $b>1$
be an integer and
$b>1$
be an integer and
![]() $B\subset \{0,\ldots ,b-1\}.$
Let
$B\subset \{0,\ldots ,b-1\}.$
Let
 $A_{b}^{B}$
be the set
$A_{b}^{B}$
be the set
 $$ \begin{align*} &\overline{\{x\in [0,1]\setminus\mathbb{Q}:\text{ the }{b}\text{-ary expansion of }{x}\text{ contains only digits in }B \}}\\ &\ \ ={\{x\in [0,1]:\text{ some }{b}\text{-ary expansion of }{x}\text{ contains only digits in }B \}}. \end{align*} $$
$$ \begin{align*} &\overline{\{x\in [0,1]\setminus\mathbb{Q}:\text{ the }{b}\text{-ary expansion of }{x}\text{ contains only digits in }B \}}\\ &\ \ ={\{x\in [0,1]:\text{ some }{b}\text{-ary expansion of }{x}\text{ contains only digits in }B \}}. \end{align*} $$
Then
 $A_{b}^{B}$
is self-similar with
$A_{b}^{B}$
is self-similar with
![]() $\Lambda =B$
, and for
$\Lambda =B$
, and for
![]() $z\in B,$
the linear map
$z\in B,$
the linear map
![]() $f_{z}$
is as follows:
$f_{z}$
is as follows:
 $$ \begin{align*} x\in\mathbb{R}\to f_{z}(x)=\frac{1}{b}x+\frac{z}{b}. \end{align*} $$
$$ \begin{align*} x\in\mathbb{R}\to f_{z}(x)=\frac{1}{b}x+\frac{z}{b}. \end{align*} $$
To verify that
![]() $\mathcal {F}=\{f_{z}\}_{z\in B}$
has the open set condition, we can choose
$\mathcal {F}=\{f_{z}\}_{z\in B}$
has the open set condition, we can choose
![]() $U=(0,1).$
A famous example of this kind is the middle third Cantor set
$U=(0,1).$
A famous example of this kind is the middle third Cantor set
 $A^{\{0,2\}}_{3}$
.
$A^{\{0,2\}}_{3}$
.
3.3 Thickness, intersection, and sums of Cantor sets
Let
![]() $A\subset \mathbb {R}$
be a compact, totally disconnected set without isolated points. We shall call A a Cantor set. First, we assume that
$A\subset \mathbb {R}$
be a compact, totally disconnected set without isolated points. We shall call A a Cantor set. First, we assume that
![]() $A\subset [0,1]$
and the convex hull of A is
$A\subset [0,1]$
and the convex hull of A is
![]() $[0,1].$
In this case, we see that
$[0,1].$
In this case, we see that
![]() $\mathbb {R}\setminus A$
is a countable union of disjoint open intervals
$\mathbb {R}\setminus A$
is a countable union of disjoint open intervals
![]() $\{I_{i}\}_{i\geq 1}$
. Notice that
$\{I_{i}\}_{i\geq 1}$
. Notice that
![]() $(-\infty ,0), (1,\infty )$
are the only unbounded intervals in
$(-\infty ,0), (1,\infty )$
are the only unbounded intervals in
![]() $\{I_{i}\}_{i\geq 1}.$
We call bounded intervals in
$\{I_{i}\}_{i\geq 1}.$
We call bounded intervals in
![]() $\{I_{i}\}_{i\geq 1}$
to be bounded gaps of
$\{I_{i}\}_{i\geq 1}$
to be bounded gaps of
![]() $A.$
Thus, A can be constructed by iteratively chopping out open intervals from
$A.$
Thus, A can be constructed by iteratively chopping out open intervals from
![]() $\mathbb {R}.$
Let
$\mathbb {R}.$
Let
![]() $I=(a,b)$
be one of those bounded open intervals. We find the interval
$I=(a,b)$
be one of those bounded open intervals. We find the interval
![]() $I^{-}\in \{I_{i}\}_{i\geq 0}$
and
$I^{-}\in \{I_{i}\}_{i\geq 0}$
and
![]() $I^{-}\subset (-\infty , a)$
such that
$I^{-}\subset (-\infty , a)$
such that
![]() $\lvert I^{-}\rvert \geq \lvert I\rvert $
and there is no other such interval between
$\lvert I^{-}\rvert \geq \lvert I\rvert $
and there is no other such interval between
![]() $I^{-}$
and
$I^{-}$
and
![]() $I.$
Similarly, we can find
$I.$
Similarly, we can find
![]() $I^{+}\subset (b,\infty )$
to the right of
$I^{+}\subset (b,\infty )$
to the right of
![]() $I.$
Suppose that
$I.$
Suppose that
![]() $I^{-}=(c,d)$
and
$I^{-}=(c,d)$
and
![]() $I^{+}=(e,f).$
We see that
$I^{+}=(e,f).$
We see that
Let
![]() $b_{L}=a-d$
,
$b_{L}=a-d$
,
![]() $b_{R}=e-b$
and
$b_{R}=e-b$
and
We define
![]() $C(A)=\inf _{I\in \{I_{i}\}_{i\geq 1}, I \text { bounded}} C(I).$
This number
$C(A)=\inf _{I\in \{I_{i}\}_{i\geq 1}, I \text { bounded}} C(I).$
This number
![]() $C(A)$
is called the thickness of
$C(A)$
is called the thickness of
![]() $A.$
We also define the normalized thickness of A to be
$A.$
We also define the normalized thickness of A to be
 $$ \begin{align*} S(A)=\frac{C(A)}{C(A)+1}. \end{align*} $$
$$ \begin{align*} S(A)=\frac{C(A)}{C(A)+1}. \end{align*} $$
For a general Cantor set A, we can perform a uniquely determined orientation-preserving affine transformation T which maps the convex hull of A to the unit interval. Then we define
We have the following result due to Newhouse. See [Reference Newhouse14].
Theorem 3.2. (Newhouse’s gap lemma)
Let
![]() $A,B$
be two compact, totally disconnected sets. Suppose that A is not contained in any of the gaps of B and vice versa. If
$A,B$
be two compact, totally disconnected sets. Suppose that A is not contained in any of the gaps of B and vice versa. If
![]() $S(A)+S(B)\geq 1,$
then
$S(A)+S(B)\geq 1,$
then
![]() $A\cap B\neq \emptyset .$
$A\cap B\neq \emptyset .$
Newhouse proved the above result with the condition
![]() $S(A)+S(B)>1.$
Astels [Reference Astels1, Theorem 2.2] showed that the above result holds for
$S(A)+S(B)>1.$
Astels [Reference Astels1, Theorem 2.2] showed that the above result holds for
![]() $S(A)+S(B)=1$
as well.
$S(A)+S(B)=1$
as well.
In the case when we have two very thick Cantor sets, we expect that their intersection could also be very thick. In this direction, we have [Reference Hunt, Kan and Yorke10, Theorem 1, and the discussion at the beginning of p. 882, and the discussion before Corollary 6].
Theorem 3.3. Let
![]() $A,B$
be two compact, totally disconnected sets. Suppose that A is not contained in any of the gaps of B and vice versa. For each
$A,B$
be two compact, totally disconnected sets. Suppose that A is not contained in any of the gaps of B and vice versa. For each
![]() $\delta>0,$
there is an
$\delta>0,$
there is an
![]() $\epsilon>0$
such that if
$\epsilon>0$
such that if
![]() $S(A), S(B)$
are greater than
$S(A), S(B)$
are greater than
![]() $1-\epsilon ,$
then there is a compact set
$1-\epsilon ,$
then there is a compact set
![]() $C\subset A\cap B$
such that
$C\subset A\cap B$
such that
![]() $S(C)$
is greater than
$S(C)$
is greater than
![]() $1-\delta .$
Moreover, suppose that the convex hulls
$1-\delta .$
Moreover, suppose that the convex hulls
![]() $\mathrm{Conv(A),Conv(B)}$
are such that
$\mathrm{Conv(A),Conv(B)}$
are such that
![]() $\mathrm{Conv(A)}\cap \mathrm{Conv(B)}$
contains neither A nor B. Then by making
$\mathrm{Conv(A)}\cap \mathrm{Conv(B)}$
contains neither A nor B. Then by making
![]() $\epsilon $
smaller if necessary, C can be chosen so that
$\epsilon $
smaller if necessary, C can be chosen so that
![]() $\lvert \mathrm{Conv(C)}\rvert $
is at least
$\lvert \mathrm{Conv(C)}\rvert $
is at least
![]() $(1-\delta )\lvert \mathrm{Conv(A)}\cap \mathrm{Conv(B)}\rvert $
.
$(1-\delta )\lvert \mathrm{Conv(A)}\cap \mathrm{Conv(B)}\rvert $
.
Recently, there are some further development on the intersecting structures of thick Cantor sets. See [Reference Yavicoli19].
The following result was proved in [Reference Astels1, Theorem 2.4].
Theorem 3.4. Let
![]() $A_{1},\ldots ,A_{k}$
be
$A_{1},\ldots ,A_{k}$
be
![]() $k\geq 2$
Cantor sets. Suppose that their convex hulls are
$k\geq 2$
Cantor sets. Suppose that their convex hulls are
![]() $I_{1},I_{2},\ldots ,I_{k}$
and the size of their largest bounded gaps are
$I_{1},I_{2},\ldots ,I_{k}$
and the size of their largest bounded gaps are
![]() $g_{1},\ldots ,g_{k}$
respectively. Suppose further that
$g_{1},\ldots ,g_{k}$
respectively. Suppose further that
 $\sum _{i=1}^{k} S(A_{i})\geq 1$
and
$\sum _{i=1}^{k} S(A_{i})\geq 1$
and
![]() $\min \{\lvert I_{1}\rvert ,\ldots ,\lvert I_{k}\rvert \}> \max \{g_{1},\ldots ,g_{k}\}.$
Then
$\min \{\lvert I_{1}\rvert ,\ldots ,\lvert I_{k}\rvert \}> \max \{g_{1},\ldots ,g_{k}\}.$
Then
![]() $A_{1}+\cdots +A_{k}$
is an interval.
$A_{1}+\cdots +A_{k}$
is an interval.
For later use, we reformulate the above result in terms of intersections. Let
![]() $A_{1},A_{2},A_{3}$
be three Cantor sets satisfying the hypothesis of the above theorem. Consider the Cartesian product
$A_{1},A_{2},A_{3}$
be three Cantor sets satisfying the hypothesis of the above theorem. Consider the Cartesian product
![]() $A=A_{1}\times A_{2}\times A_{3}.$
Let
$A=A_{1}\times A_{2}\times A_{3}.$
Let
![]() $v\in S^{2}$
be a direction vector of
$v\in S^{2}$
be a direction vector of
![]() $\mathbb {R}^{3}$
and let
$\mathbb {R}^{3}$
and let
![]() $H_{v}$
be the plane passing through the origin and normal to
$H_{v}$
be the plane passing through the origin and normal to
![]() $v.$
The family of planes parallel to
$v.$
The family of planes parallel to
![]() $H_{v}$
can be parameterized by
$H_{v}$
can be parameterized by
![]() $\mathbb {R},$
more precisely,
$\mathbb {R},$
more precisely,
![]() $\{H_{v}(a)=H_{v}+av\}_{a\in \mathbb {R}}.$
Denote
$\{H_{v}(a)=H_{v}+av\}_{a\in \mathbb {R}}.$
Denote
![]() $P_{v}:\mathbb {R}^{3}\to \mathbb {R}v$
to be the corresponding orthogonal projection in direction v. The above theorem says that
$P_{v}:\mathbb {R}^{3}\to \mathbb {R}v$
to be the corresponding orthogonal projection in direction v. The above theorem says that
![]() $P_{(1/\sqrt {3},1/\sqrt {3},1/\sqrt {3})}(A)$
is an interval. Moreover, notice that the normalized thickness is invariant under affine maps. In addition, there is a non-empty open neighborhood O of
$P_{(1/\sqrt {3},1/\sqrt {3},1/\sqrt {3})}(A)$
is an interval. Moreover, notice that the normalized thickness is invariant under affine maps. In addition, there is a non-empty open neighborhood O of
![]() $(1/\sqrt {3},1/\sqrt {3},1/\sqrt {3})$
in
$(1/\sqrt {3},1/\sqrt {3},1/\sqrt {3})$
in
![]() $S^{2}$
such that whenever
$S^{2}$
such that whenever
![]() $v=(v_{1},v_{2},v_{3})\in O,$
the size of the minimum convex hull of
$v=(v_{1},v_{2},v_{3})\in O,$
the size of the minimum convex hull of
![]() $v_{1}A_{1}, v_{2}A_{2}, v_{3}A_{3}$
is larger than the size of their maximum gap. This implies that
$v_{1}A_{1}, v_{2}A_{2}, v_{3}A_{3}$
is larger than the size of their maximum gap. This implies that
![]() $P_{v}(A)$
is an interval.
$P_{v}(A)$
is an interval.
Now if
![]() $\Pi _{v}(A)$
is an interval, then we see that
$\Pi _{v}(A)$
is an interval, then we see that
is an interval. More precisely, if
![]() $H_{v}(a)\cap I_{1}\times I_{2}\times I_{3}\neq \emptyset $
, then we have
$H_{v}(a)\cap I_{1}\times I_{2}\times I_{3}\neq \emptyset $
, then we have
![]() $H_{v}(a)\cap A\neq \emptyset .$
From here, we have the following corollary.
$H_{v}(a)\cap A\neq \emptyset .$
From here, we have the following corollary.
Corollary 3.5. Let
![]() $A_{1},A_{2},A_{3}$
be
$A_{1},A_{2},A_{3}$
be
![]() $3$
Cantor sets with
$3$
Cantor sets with
![]() $S(A_{1})+S(A_{2})+S(A_{3})\geq 1.$
Suppose that their convex hulls are
$S(A_{1})+S(A_{2})+S(A_{3})\geq 1.$
Suppose that their convex hulls are
![]() $I_{1},I_{2},I_{3}$
and the size of their largest gaps are
$I_{1},I_{2},I_{3}$
and the size of their largest gaps are
![]() $g_{1},g_{2},g_{3}$
respectively. If
$g_{1},g_{2},g_{3}$
respectively. If
then there is a non-empty open set
![]() $O\subset S^{2}$
such that whenever
$O\subset S^{2}$
such that whenever
![]() $v\in O,$
we have
$v\in O,$
we have
We now compute the normalized thickness of some examples of Cantor sets. First, let
![]() $b>2$
be an integer and let
$b>2$
be an integer and let
![]() $B=\{0,1,\ldots ,l\}$
where
$B=\{0,1,\ldots ,l\}$
where
![]() $l<b-1.$
We consider the set
$l<b-1.$
We consider the set
 $$ \begin{align*} A^{B}_{b}=\{x\in [0,1]: \text{ some }{b}\text{-ary expansion of }{x}\text{ contains only digits in }B \}. \end{align*} $$
$$ \begin{align*} A^{B}_{b}=\{x\in [0,1]: \text{ some }{b}\text{-ary expansion of }{x}\text{ contains only digits in }B \}. \end{align*} $$
Lemma 3.6. Let
 $b,B, A^{B}_{b}$
be as above. The normalized thickness of
$b,B, A^{B}_{b}$
be as above. The normalized thickness of
 $A^{B}_{b}$
is
$A^{B}_{b}$
is
 $$ \begin{align*} S(A^{B}_{b})=\frac{l}{b-1}. \end{align*} $$
$$ \begin{align*} S(A^{B}_{b})=\frac{l}{b-1}. \end{align*} $$
Proof. The convex hull of
 $A^{B}_{b}$
is
$A^{B}_{b}$
is
![]() $[0,a]$
, where
$[0,a]$
, where
 $$ \begin{align*} a=\sum_{i=1}^{\infty} \frac{l}{b^{i}}=\frac{l}{b-1}. \end{align*} $$
$$ \begin{align*} a=\sum_{i=1}^{\infty} \frac{l}{b^{i}}=\frac{l}{b-1}. \end{align*} $$
The largest gaps of
 $A^{B}_{b}$
are of size
$A^{B}_{b}$
are of size
 $$ \begin{align*} \frac{b-1-l}{b(b-1)}. \end{align*} $$
$$ \begin{align*} \frac{b-1-l}{b(b-1)}. \end{align*} $$
Those gaps are located in each of the intervals
Let I be one of those gaps. Then we see that
 $$ \begin{align*} C(I)=\frac{l}{b-1-l}. \end{align*} $$
$$ \begin{align*} C(I)=\frac{l}{b-1-l}. \end{align*} $$
From here and the fact that
 $A^{B}_{b}$
is self-similar, we see that
$A^{B}_{b}$
is self-similar, we see that
 $C(A^{B}_{b})=l/(b-1-l)$
and
$C(A^{B}_{b})=l/(b-1-l)$
and
 $S(A^{B}_{b})=l/(b-1).$
$S(A^{B}_{b})=l/(b-1).$
Next, we consider the middle third Cantor set
 $C_{3}=A^{\{0,2\}}_{3}.$
Following the above steps, we see that
$C_{3}=A^{\{0,2\}}_{3}.$
Following the above steps, we see that
![]() $C(C_{3})=1, S(C_{3})=1/2.$
Let
$C(C_{3})=1, S(C_{3})=1/2.$
Let
![]() $k>1$
. We consider the image of
$k>1$
. We consider the image of
![]() $C_{3}$
under the map
$C_{3}$
under the map
![]() $x\to x^{k}.$
We write this image as
$x\to x^{k}.$
We write this image as
 $C^{k}_{3}.$
We record here a simple observation which illustrates an application of the thickness of the Cantor set.
$C^{k}_{3}.$
We record here a simple observation which illustrates an application of the thickness of the Cantor set.
Theorem 3.7. For all
![]() $x\in [0,4]$
, there exist
$x\in [0,4]$
, there exist
![]() $x_{1},x_{2},x_{3},x_{4}\in C_{3}$
such that
$x_{1},x_{2},x_{3},x_{4}\in C_{3}$
such that
 $$ \begin{align*} x=x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}. \end{align*} $$
$$ \begin{align*} x=x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}. \end{align*} $$
More generally, for each number
![]() $k>1$
, there is an integer
$k>1$
, there is an integer
![]() $1<n(k)\leq 2^{k}$
such that all
$1<n(k)\leq 2^{k}$
such that all
![]() $x\in [0,n(k)]$
can be written as
$x\in [0,n(k)]$
can be written as
 $$ \begin{align*} x=\sum_{i=1}^{n(k)}x_{i}^{k}, \end{align*} $$
$$ \begin{align*} x=\sum_{i=1}^{n(k)}x_{i}^{k}, \end{align*} $$
where
![]() $x_{1},\ldots ,x_{n(k)}\in C_{3}.$
$x_{1},\ldots ,x_{n(k)}\in C_{3}.$
(We were told by S. Chow that this result (for
![]() $k=2$
) was conjectured in [Reference Athreya, Reznick and Tyson2, Conjecture 13] and answered in [Reference Jiang, Li, Wang and Zhao12]. We thank him for providing the references.)
$k=2$
) was conjectured in [Reference Athreya, Reznick and Tyson2, Conjecture 13] and answered in [Reference Jiang, Li, Wang and Zhao12]. We thank him for providing the references.)
Lemma 3.8. Let
 $k,C^{k}_{3}$
be as above. Then
$k,C^{k}_{3}$
be as above. Then
 $$ \begin{align*} S(C^{k}_{3})=\frac{1}{2^{k}}. \end{align*} $$
$$ \begin{align*} S(C^{k}_{3})=\frac{1}{2^{k}}. \end{align*} $$
Proof. Suppose that
![]() $I=(a,a+\Delta )$
is a bounded gap of
$I=(a,a+\Delta )$
is a bounded gap of
![]() $C_{3}.$
Then we see that the next gap on the right of I which is not smaller than I has a left endpoint
$C_{3}.$
Then we see that the next gap on the right of I which is not smaller than I has a left endpoint
![]() $a+2\Delta .$
Similarly, the next gap on the left of I which is not smaller than I has a right endpoint
$a+2\Delta .$
Similarly, the next gap on the left of I which is not smaller than I has a right endpoint
![]() $a-\Delta .$
For the middle third Cantor set
$a-\Delta .$
For the middle third Cantor set
![]() $C_{3},$
we always have
$C_{3},$
we always have
![]() $a\geq \Delta .$
$a\geq \Delta .$
After taking the k-th power map, we have points
The gap I is now transformed into a gap of size
This length is increasing as a function of a as well as
![]() $\Delta .$
Thus we see that the number
$\Delta .$
Thus we see that the number
![]() $b_{L}$
in the definition of thickness is at least
$b_{L}$
in the definition of thickness is at least
![]() $\lvert (a-\Delta )^{k}-a^{k}\rvert $
. We need to take care of
$\lvert (a-\Delta )^{k}-a^{k}\rvert $
. We need to take care of
![]() $b_{R}.$
By the above argument, we see that
$b_{R}.$
By the above argument, we see that
![]() $b_{R}$
is at most
$b_{R}$
is at most
![]() $(a+2\Delta )^{k}-(a+\Delta )^{k}.$
However, we need a lower bound for
$(a+2\Delta )^{k}-(a+\Delta )^{k}.$
However, we need a lower bound for
![]() $b_{R}.$
To do this, we need to study how the gaps of
$b_{R}.$
To do this, we need to study how the gaps of
![]() $C_{3}$
in
$C_{3}$
in
![]() $[a+\Delta ,a+2\Delta ]$
are transformed under the map
$[a+\Delta ,a+2\Delta ]$
are transformed under the map
![]() $x\to x^{k}.$
Notice that a gap inside
$x\to x^{k}.$
Notice that a gap inside
![]() $[a+\Delta , a+2\Delta ]$
might become larger than
$[a+\Delta , a+2\Delta ]$
might become larger than
![]() $\lvert a^{k}- (a+\Delta )^{k}\rvert $
after taking the k-th power. Note that by the convexity of
$\lvert a^{k}- (a+\Delta )^{k}\rvert $
after taking the k-th power. Note that by the convexity of
![]() $x\to x^{k},$
there is a
$x\to x^{k},$
there is a
![]() $\delta \in (0,\Delta ]$
such that
$\delta \in (0,\Delta ]$
such that
Let
![]() $(a+\Delta +\alpha ,a+\Delta +\alpha +\beta )$
be a bounded gap of
$(a+\Delta +\alpha ,a+\Delta +\alpha +\beta )$
be a bounded gap of
![]() $C_{3}\cap [a+\Delta ,a+2\Delta ]$
with
$C_{3}\cap [a+\Delta ,a+2\Delta ]$
with
![]() $\alpha , \beta>0$
and
$\alpha , \beta>0$
and
![]() $\alpha +\beta \leq \Delta .$
Then we have
$\alpha +\beta \leq \Delta .$
Then we have
![]() $\beta \leq \alpha .$
This follows by self-similarity, since
$\beta \leq \alpha .$
This follows by self-similarity, since
![]() $[a+\Delta ,a+2\Delta ]$
is a similar copy of
$[a+\Delta ,a+2\Delta ]$
is a similar copy of
![]() $C_{3}$
with contraction factor
$C_{3}$
with contraction factor
![]() $\Delta .$
From here, we see that to find gaps of
$\Delta .$
From here, we see that to find gaps of
![]() $C^{k}_{3}$
on the right side of
$C^{k}_{3}$
on the right side of
![]() $(a+\Delta )^{k}$
with length at least
$(a+\Delta )^{k}$
with length at least
![]() $\lvert a^{k}-(a+\Delta )^{k}\rvert $
, one has to search the gaps of
$\lvert a^{k}-(a+\Delta )^{k}\rvert $
, one has to search the gaps of
![]() $C^{k}_{3}$
in
$C^{k}_{3}$
in
![]() $[(a+\Delta +\delta )^{k},\infty ).$
Thus
$[(a+\Delta +\delta )^{k},\infty ).$
Thus
![]() $b_{R}$
is at least
$b_{R}$
is at least
Observe that for
![]() $x=\delta /(a+\Delta ),$
$x=\delta /(a+\Delta ),$
 $$ \begin{align*} \frac{b_{R}}{(a+\Delta)^{k}-a^{k}}\geq\frac{(a+\Delta+\delta)^{k}-(a+\Delta)^{k}}{(a+\Delta+2\delta)^{k}-(a+\Delta+\delta)^{k}} = \frac{(1+x)^{k}-1}{(1+2x)^{k}-(1+x)^{k}}. \end{align*} $$
$$ \begin{align*} \frac{b_{R}}{(a+\Delta)^{k}-a^{k}}\geq\frac{(a+\Delta+\delta)^{k}-(a+\Delta)^{k}}{(a+\Delta+2\delta)^{k}-(a+\Delta+\delta)^{k}} = \frac{(1+x)^{k}-1}{(1+2x)^{k}-(1+x)^{k}}. \end{align*} $$
Since
![]() $0<\delta \leq \Delta \leq a,$
we see that the above is at least (the value when
$0<\delta \leq \Delta \leq a,$
we see that the above is at least (the value when
![]() $x=1/2$
)
$x=1/2$
)
 $$ \begin{align*} c_{k}=\frac{1.5^{k}-1}{2^{k}-1.5^{k}}. \end{align*} $$
$$ \begin{align*} c_{k}=\frac{1.5^{k}-1}{2^{k}-1.5^{k}}. \end{align*} $$
It follows that
![]() $b_{R}\geq c_{k}((a+\Delta )^{k}-a^{k}).$
We see that
$b_{R}\geq c_{k}((a+\Delta )^{k}-a^{k}).$
We see that
 $$ \begin{align} \min\{b_{L},b_{R}\}/\lvert a^{k}- (a+\Delta)^{k}\rvert \geq\min\bigg\{\frac{a^{k}-(a-\Delta)^{k}}{(a+\Delta)^{k}-a^{k}},c_{k}\bigg\}\geq \frac{1}{2^{k}-1}. \end{align} $$
$$ \begin{align} \min\{b_{L},b_{R}\}/\lvert a^{k}- (a+\Delta)^{k}\rvert \geq\min\bigg\{\frac{a^{k}-(a-\Delta)^{k}}{(a+\Delta)^{k}-a^{k}},c_{k}\bigg\}\geq \frac{1}{2^{k}-1}. \end{align} $$
For the last inequality, notice that
 $$ \begin{align*} \frac{a^{k}-(a-\Delta)^{k}}{(a+\Delta)^{k}-a^{k}}=\frac{1-(1-\Delta/a)^{k}}{(1+\Delta/a)^{k}-1}. \end{align*} $$
$$ \begin{align*} \frac{a^{k}-(a-\Delta)^{k}}{(a+\Delta)^{k}-a^{k}}=\frac{1-(1-\Delta/a)^{k}}{(1+\Delta/a)^{k}-1}. \end{align*} $$
As
![]() $(a,a+\Delta )$
is a bounded gap of
$(a,a+\Delta )$
is a bounded gap of
![]() $C_{3},$
we see that
$C_{3},$
we see that
![]() $0<\Delta \leq a.$
The function
$0<\Delta \leq a.$
The function
 $$ \begin{align*} x\in [0,1]\to \frac{1-(1-x)^{k}}{(1+x)^{k}-1} \end{align*} $$
$$ \begin{align*} x\in [0,1]\to \frac{1-(1-x)^{k}}{(1+x)^{k}-1} \end{align*} $$
takes the minimum at
![]() $x=1$
with the value
$x=1$
with the value
![]() $1/(2^{k}-1).$
For all
$1/(2^{k}-1).$
For all
![]() $k>1,$
we have
$k>1,$
we have
 $$ \begin{align*} \frac{1}{2^{k}-1}\leq \frac{1.5^{k}-1}{2^{k}-1.5^{k}}. \end{align*} $$
$$ \begin{align*} \frac{1}{2^{k}-1}\leq \frac{1.5^{k}-1}{2^{k}-1.5^{k}}. \end{align*} $$
From here, we conclude (2). As (2) holds for all bounded gaps of
![]() $C^{k}_{3}$
, we see that
$C^{k}_{3}$
, we see that
 $$ \begin{align*} C(C^{k}_{3})\geq \frac{1}{2^{k}-1} \end{align*} $$
$$ \begin{align*} C(C^{k}_{3})\geq \frac{1}{2^{k}-1} \end{align*} $$
and
 $$ \begin{align*} S(C^{k}_{3})\geq \frac{1}{2^{k}}. \end{align*} $$
$$ \begin{align*} S(C^{k}_{3})\geq \frac{1}{2^{k}}. \end{align*} $$
However, let
![]() $n\geq 1$
be an integer. Then
$n\geq 1$
be an integer. Then
![]() $I=(3^{-n},2\times 3^{-n})$
is a bounded gap of
$I=(3^{-n},2\times 3^{-n})$
is a bounded gap of
![]() $C_{3}.$
Now, in
$C_{3}.$
Now, in
![]() $C_{3},$
the next gap on the left of I with length at least
$C_{3},$
the next gap on the left of I with length at least
![]() $\lvert I\rvert $
is an infinite gap, that is,
$\lvert I\rvert $
is an infinite gap, that is,
![]() $(-\infty ,0).$
Thus in
$(-\infty ,0).$
Thus in
 $C_{3}^{k},$
the next gap on the left of
$C_{3}^{k},$
the next gap on the left of
![]() $(3^{-kn},2^{k}3^{-kn})$
with at least the same length is again
$(3^{-kn},2^{k}3^{-kn})$
with at least the same length is again
![]() $(-\infty ,0).$
This shows that the inequality (2) is sharp and the proof concludes.
$(-\infty ,0).$
This shows that the inequality (2) is sharp and the proof concludes.
From here, we see that Theorem 3.7 follows.
4 Radial projections of fractal sets: general overview
Let
![]() $d\geq 2$
be an integer. Let
$d\geq 2$
be an integer. Let
![]() $x\in \mathbb {R}^{d}$
be a point. Recall that
$x\in \mathbb {R}^{d}$
be a point. Recall that
![]() $\Pi _{x}$
is defined as follows:
$\Pi _{x}$
is defined as follows:
 $$ \begin{align*} \Pi_{x}(y)=\frac{y-x}{\lvert x-y\rvert}\in S^{d-1} \end{align*} $$
$$ \begin{align*} \Pi_{x}(y)=\frac{y-x}{\lvert x-y\rvert}\in S^{d-1} \end{align*} $$
for
![]() $y\neq x.$
The following result was proved in [Reference Orponen15].
$y\neq x.$
The following result was proved in [Reference Orponen15].
Theorem 4.1. Let
![]() $d\geq 2$
be an integer. Let
$d\geq 2$
be an integer. Let
![]() $A\subset \mathbb {R}^{d}$
be a Borel set with
$A\subset \mathbb {R}^{d}$
be a Borel set with
![]() ${\dim _{\mathrm {H}}} A>d-1.$
Then
${\dim _{\mathrm {H}}} A>d-1.$
Then
![]() $\Pi _{x}(A)$
has positive Lebesgue measure for almost all
$\Pi _{x}(A)$
has positive Lebesgue measure for almost all
![]() $x\in \mathbb {R}^{d}.$
$x\in \mathbb {R}^{d}.$
Intuitively speaking, the above theorem says that if
![]() $A\subset \mathbb {R}^{d}$
is large enough, then
$A\subset \mathbb {R}^{d}$
is large enough, then
![]() $\Pi _{x}(A)$
should also be large enough, at least generically. If the set A is a Cartesian product of self-similar sets with the open set condition, we believe that a much stronger result should hold. See Conjecture 2.1. In our situation, it is convenient to explicitly state a special case.
$\Pi _{x}(A)$
should also be large enough, at least generically. If the set A is a Cartesian product of self-similar sets with the open set condition, we believe that a much stronger result should hold. See Conjecture 2.1. In our situation, it is convenient to explicitly state a special case.
Conjecture 4.2. Let
![]() $d>1$
be an integer. Let
$d>1$
be an integer. Let
![]() $b_{1},\ldots ,b_{d}>1$
be integers. For each
$b_{1},\ldots ,b_{d}>1$
be integers. For each
![]() $i\in \{1,\ldots ,d\}$
, let
$i\in \{1,\ldots ,d\}$
, let
![]() $B_{1}\in \{0,\ldots ,b_{i}-1\}$
be a choice of digits in base
$B_{1}\in \{0,\ldots ,b_{i}-1\}$
be a choice of digits in base
![]() $b_{i}$
and
$b_{i}$
and
Consider the set
![]() $A=A_{1}\times \cdots \times A_{d}.$
If
$A=A_{1}\times \cdots \times A_{d}.$
If
![]() ${\dim _{\mathrm {H}}} A>d-1,$
then
${\dim _{\mathrm {H}}} A>d-1,$
then
![]() $\Pi _{x} (A)$
has positive Lebesgue measure for all
$\Pi _{x} (A)$
has positive Lebesgue measure for all
![]() $x\in \mathbb {R}^{d}.$
If moreover
$x\in \mathbb {R}^{d}.$
If moreover
![]() $b_{1},\ldots ,b_{d}$
are multiplicatively independent, then
$b_{1},\ldots ,b_{d}$
are multiplicatively independent, then
![]() $\Pi _{x}(A)$
contains a non-empty interior for all
$\Pi _{x}(A)$
contains a non-empty interior for all
![]() $x\in \mathbb {R}^{d}.$
$x\in \mathbb {R}^{d}.$
As
![]() $A_{1},\ldots ,A_{d}$
are self-similar sets with the open set condition, this conjecture is indeed a special case of Conjecture 2.1 under the multiplicative independence of
$A_{1},\ldots ,A_{d}$
are self-similar sets with the open set condition, this conjecture is indeed a special case of Conjecture 2.1 under the multiplicative independence of
![]() $b_{1},\ldots ,b_{d}.$
We believe that for the positivity of the Lebesgue measure, it is not necessary to require the multiplicative independence of
$b_{1},\ldots ,b_{d}.$
We believe that for the positivity of the Lebesgue measure, it is not necessary to require the multiplicative independence of
![]() $b_{1},\ldots ,b_{d}.$
Currently, almost nothing is known towards Conjectures 2.1, 4.2. For Conjecture 2.1, see [Reference Hochman and Shmerkin9] or [Reference Shmerkin17] for related results. Although results in [Reference Hochman and Shmerkin9, Reference Shmerkin17] are for linear projections rather than radial projections, it is possible to use the arguments to prove results for linear projections. For example, let A be as in Conjecture 2.1 with
$b_{1},\ldots ,b_{d}.$
Currently, almost nothing is known towards Conjectures 2.1, 4.2. For Conjecture 2.1, see [Reference Hochman and Shmerkin9] or [Reference Shmerkin17] for related results. Although results in [Reference Hochman and Shmerkin9, Reference Shmerkin17] are for linear projections rather than radial projections, it is possible to use the arguments to prove results for linear projections. For example, let A be as in Conjecture 2.1 with
![]() $d=2.$
Results in [Reference Shmerkin17] provide estimates of the size
$d=2.$
Results in [Reference Shmerkin17] provide estimates of the size
![]() $l^{\delta }\cap A$
(
$l^{\delta }\cap A$
(
![]() $l^{\delta }$
is the
$l^{\delta }$
is the
![]() $\delta $
-neighborhood of l) uniformly across
$\delta $
-neighborhood of l) uniformly across
![]() $\delta>0$
and lines
$\delta>0$
and lines
![]() $l\subset \mathbb {R}^{2}$
with direction strictly away from being parallel with the coordinate axes. In particular, for each
$l\subset \mathbb {R}^{2}$
with direction strictly away from being parallel with the coordinate axes. In particular, for each
![]() $\epsilon>0,$
for all small enough
$\epsilon>0,$
for all small enough
![]() $\delta>0$
and all lines l, to cover
$\delta>0$
and all lines l, to cover
![]() $l^{\delta }\cap A,$
it is enough to use at most
$l^{\delta }\cap A,$
it is enough to use at most
![]() $\delta ^{-({\dim _{\mathrm {H}}} A-1+\epsilon )}$
many
$\delta ^{-({\dim _{\mathrm {H}}} A-1+\epsilon )}$
many
![]() $\delta $
-balls. Using this estimate, we can conclude that
$\delta $
-balls. Using this estimate, we can conclude that
![]() $\Pi _{(0,0)}A$
cannot be small. In fact, suppose that
$\Pi _{(0,0)}A$
cannot be small. In fact, suppose that
![]() $\Pi _{(0,0)}A$
can be covered by at most
$\Pi _{(0,0)}A$
can be covered by at most
![]() $0.0001\delta ^{-(1-2\epsilon )}$
many
$0.0001\delta ^{-(1-2\epsilon )}$
many
![]() $\delta $
-balls. Then we are forced to have a fiber of
$\delta $
-balls. Then we are forced to have a fiber of
![]() $\Pi _{(0,0)}(A)$
which cannot be covered by
$\Pi _{(0,0)}(A)$
which cannot be covered by
many
![]() $\delta $
-balls. Fibers of
$\delta $
-balls. Fibers of
![]() $\Pi _{(0,0)}(A)$
are lines passing through the origin. In particular, this contradicts with the results in [Reference Shmerkin17]. From here, we conclude that
$\Pi _{(0,0)}(A)$
are lines passing through the origin. In particular, this contradicts with the results in [Reference Shmerkin17]. From here, we conclude that
![]() ${\dim _{\mathrm {B}}} \Pi _{(0,0)}A=1.$
Here,
${\dim _{\mathrm {B}}} \Pi _{(0,0)}A=1.$
Here,
![]() ${\dim _{\mathrm {B}}} \Pi _{(0,0)}A$
is the box dimension of
${\dim _{\mathrm {B}}} \Pi _{(0,0)}A$
is the box dimension of
![]() $\Pi _{(0,0)}A$
. It is possible to upgrade this result to
$\Pi _{(0,0)}A$
. It is possible to upgrade this result to
![]() ${\dim _{\mathrm {H}}} \Pi _{(0,0)}A=1$
by carefully studying a certain regular measure
${\dim _{\mathrm {H}}} \Pi _{(0,0)}A=1$
by carefully studying a certain regular measure
![]() $\mu $
supported on A and its image under
$\mu $
supported on A and its image under
![]() $\Pi _{(0,0)}.$
Of course,
$\Pi _{(0,0)}.$
Of course,
![]() $(0,0)$
can be replaced with any other point in
$(0,0)$
can be replaced with any other point in
![]() $\mathbb {R}^{2}.$
$\mathbb {R}^{2}.$
5 Proofs of Theorems 2.2, 2.4, 2.5, and 2.7
Now we prove Theorem 2.2.
Proof of Theorem 2.2
Consider the set
 $N_{3}^{B_{3}}\times N_{5}^{B_{5}}\times N_{7}^{B_{7}}$
, where
$N_{3}^{B_{3}}\times N_{5}^{B_{5}}\times N_{7}^{B_{7}}$
, where
Now we construct the sets
Then we see that [Reference Falconer7, §7.1]
![]() ${\dim _{\mathrm {H}}} A_{3}\times A_{5}\times A_{7}=\log 2/\log 3+\log 3/\log 5+\log 4/ \log 7>2.$
Let
${\dim _{\mathrm {H}}} A_{3}\times A_{5}\times A_{7}=\log 2/\log 3+\log 3/\log 5+\log 4/ \log 7>2.$
Let
![]() $\{\}$
be the fractional part symbol, that is, for a real number
$\{\}$
be the fractional part symbol, that is, for a real number
![]() $a, \{a\}\in [0,1)$
is the unique number t in
$a, \{a\}\in [0,1)$
is the unique number t in
![]() $[0,1)$
so that
$[0,1)$
so that
![]() $t-a\in \mathbb {Z}.$
For each integer
$t-a\in \mathbb {Z}.$
For each integer
![]() $k\geq 1$
, consider the line
$k\geq 1$
, consider the line
![]() $l_{k}$
passing through the origin with direction vector
$l_{k}$
passing through the origin with direction vector
If
![]() $l_{k}\cap A_{3}\times A_{5}\times A_{7}\neq \emptyset $
, then we take a point
$l_{k}\cap A_{3}\times A_{5}\times A_{7}\neq \emptyset $
, then we take a point
![]() $(x,y,z)\in l_{k}\cap A_{3}\times A_{5}\times A_{7}.$
Consider the point
$(x,y,z)\in l_{k}\cap A_{3}\times A_{5}\times A_{7}.$
Consider the point
Since
![]() $y=5^{\{k\log 3/\log 5\}} x, z=7^{\{k\log 3/\log 7\}}x$
, we see that
$y=5^{\{k\log 3/\log 5\}} x, z=7^{\{k\log 3/\log 7\}}x$
, we see that
Thus we see that
![]() $x^{\prime }=y^{\prime }=z^{\prime }.$
It is straightforward to see that the
$x^{\prime }=y^{\prime }=z^{\prime }.$
It is straightforward to see that the
![]() $3$
-ary expansion of
$3$
-ary expansion of
![]() $x^{\prime }$
contains only digits in
$x^{\prime }$
contains only digits in
![]() $B_{3}$
, the
$B_{3}$
, the
![]() $5$
-ary expansion of
$5$
-ary expansion of
![]() $y^{\prime }$
contains only digits in
$y^{\prime }$
contains only digits in
![]() $B_{5}$
, and the
$B_{5}$
, and the
![]() $7$
-ary expansion of
$7$
-ary expansion of
![]() $z^{\prime }$
contains only digits in
$z^{\prime }$
contains only digits in
![]() $B_{7}.$
Taking the integer part, we see that
$B_{7}.$
Taking the integer part, we see that
 $$ \begin{align*} [x^{\prime}]=[y^{\prime}]=[z^{\prime}] \in N_{3,5,7}^{B_{3},B_{5},B_{7}}. \end{align*} $$
$$ \begin{align*} [x^{\prime}]=[y^{\prime}]=[z^{\prime}] \in N_{3,5,7}^{B_{3},B_{5},B_{7}}. \end{align*} $$
Under Conjecture 2.1, we see that there are infinitely many integers
![]() $k\geq 1$
such that
$k\geq 1$
such that
Indeed, the direction vector of
![]() $l_{k}$
is
$l_{k}$
is
Under Schanuel’s conjecture,
![]() $1,\log 3/\log 5, \log 3/\log 7$
are linearly independent over
$1,\log 3/\log 5, \log 3/\log 7$
are linearly independent over
![]() $\mathbb {Q},$
and therefore the sequence
$\mathbb {Q},$
and therefore the sequence
equidistributes in
![]() $[0,1]^{2}.$
Thus the closure of
$[0,1]^{2}.$
Thus the closure of
![]() $\bigcup _{k\geq 0} l_{k}$
contains the cone C spanned by the origin and the set
$\bigcup _{k\geq 0} l_{k}$
contains the cone C spanned by the origin and the set
Now if
![]() $\Pi _{(0,0,0)}(A_{3}\times A_{5}\times A_{7} \cap C )$
has a non-empty interior, then
$\Pi _{(0,0,0)}(A_{3}\times A_{5}\times A_{7} \cap C )$
has a non-empty interior, then
![]() $l_{k}$
will intersect
$l_{k}$
will intersect
![]() $A_{3}\times A_{5}\times A_{7} \cap C$
infinitely often. Observe that
$A_{3}\times A_{5}\times A_{7} \cap C$
infinitely often. Observe that
![]() $A_{3}\times A_{5}\times A_{7}$
intersects the interior of
$A_{3}\times A_{5}\times A_{7}$
intersects the interior of
![]() $C.$
Thus there is a point
$C.$
Thus there is a point
![]() $a\in A_{3}\times A_{5}\times A_{7}$
and a
$a\in A_{3}\times A_{5}\times A_{7}$
and a
![]() $r>0$
such that
$r>0$
such that
![]() $B_{a}(r)\subset C.$
Since
$B_{a}(r)\subset C.$
Since
![]() $A_{3}\cap [1,2],A_{5}\cap [1,2],A_{7}\cap [1,2]$
are self-similar with contraction ratios
$A_{3}\cap [1,2],A_{5}\cap [1,2],A_{7}\cap [1,2]$
are self-similar with contraction ratios
![]() $1/3,1/5,1/7$
respectively, it is possible to find linear maps
$1/3,1/5,1/7$
respectively, it is possible to find linear maps
![]() $f_{3},f_{5},f_{7}:\mathbb {R}\to \mathbb {R}:$
$f_{3},f_{5},f_{7}:\mathbb {R}\to \mathbb {R}:$
for some positive integers
![]() $l_{3},l_{5},l_{7}$
and real numbers
$l_{3},l_{5},l_{7}$
and real numbers
![]() $t_{3},t_{5},t_{7}$
such that
$t_{3},t_{5},t_{7}$
such that
and
We denote
![]() $A^{\prime }_{3}=f_{3}(A_{3}\cap [1,2]), A^{\prime }_{5}=f_{5}(A_{5}\cap [1,2]), A^{\prime }_{7}=f_{7}(A_{7}\cap [1,2]).$
Then we see that
$A^{\prime }_{3}=f_{3}(A_{3}\cap [1,2]), A^{\prime }_{5}=f_{5}(A_{5}\cap [1,2]), A^{\prime }_{7}=f_{7}(A_{7}\cap [1,2]).$
Then we see that
Moreover, since
![]() $f_{3}\times f_{5}\times f_{7}$
is linear and invertible and thus bi-Lipschitz, by [Reference Falconer7, Corollary 2.4], we have
$f_{3}\times f_{5}\times f_{7}$
is linear and invertible and thus bi-Lipschitz, by [Reference Falconer7, Corollary 2.4], we have
 $$ \begin{align*} {\dim_{\mathrm{H}}} (A^{\prime}_{3}\times A^{\prime}_{5}\times A^{\prime}_{7})={\dim_{\mathrm{H}}}(A_{3}\times A_{5}\times A_{7}\cap [1,2]^{3}). \end{align*} $$
$$ \begin{align*} {\dim_{\mathrm{H}}} (A^{\prime}_{3}\times A^{\prime}_{5}\times A^{\prime}_{7})={\dim_{\mathrm{H}}}(A_{3}\times A_{5}\times A_{7}\cap [1,2]^{3}). \end{align*} $$
Next, observe that
![]() $A_{3}\times A_{5}\times A_{7}\cap [1,2]^{3}$
is a translation of
$A_{3}\times A_{5}\times A_{7}\cap [1,2]^{3}$
is a translation of
![]() $K_{3}\times K_{5}\times K_{7}$
, where
$K_{3}\times K_{5}\times K_{7}$
, where
By [Reference Falconer7, §7.1], we see that
![]() ${\dim _{\mathrm {H}}} K_{3}\times K_{5}\times K_{7}={\dim _{\mathrm {H}}} A_{3}\times A_{5}\times A_{7}.$
Now Conjecture 2.1 tells us that
${\dim _{\mathrm {H}}} K_{3}\times K_{5}\times K_{7}={\dim _{\mathrm {H}}} A_{3}\times A_{5}\times A_{7}.$
Now Conjecture 2.1 tells us that
![]() $\Pi _{(0,0,0)}(A^{\prime }_{3}\times A^{\prime }_{5}\times A^{\prime }_{7})$
has a non-empty interior. This proves the result.
$\Pi _{(0,0,0)}(A^{\prime }_{3}\times A^{\prime }_{5}\times A^{\prime }_{7})$
has a non-empty interior. This proves the result.
Theorem 2.4 follows by using a similar argument.
Proof of Theorem 2.4
The proof is very similar to the previous one. Let
![]() $p,q$
be two distinct odd primes. Then we see that
$p,q$
be two distinct odd primes. Then we see that
![]() $\log p/\log q$
is irrational. Consider the set
$\log p/\log q$
is irrational. Consider the set
 $N^{B_{p}}_{p}\times N^{B_{q}}_{q}$
, where
$N^{B_{p}}_{p}\times N^{B_{q}}_{q}$
, where
We also construct the sets
Now by Lemma 3.6 (applied to suitable affine copies of
![]() $A_{p},A_{q}$
), we see that
$A_{p},A_{q}$
), we see that
![]() $S(A_{p})=S(A_{q})=1/2.$
We now use Theorem 3.4. Since
$S(A_{p})=S(A_{q})=1/2.$
We now use Theorem 3.4. Since
![]() $S(A_{p})+S(A_{q})=1,$
we see that the difference set
$S(A_{p})+S(A_{q})=1,$
we see that the difference set
![]() $A_{p}-A_{q}$
is an interval (for the gap condition, observe that the largest gaps of
$A_{p}-A_{q}$
is an interval (for the gap condition, observe that the largest gaps of
![]() $A_{p},A_{q}$
are shorter than the unit interval). This says that
$A_{p},A_{q}$
are shorter than the unit interval). This says that
 $P_{(-1/\sqrt {2},1/\sqrt {2})}(A_{p}\cap A_{q})$
is an interval. The convex hull of
$P_{(-1/\sqrt {2},1/\sqrt {2})}(A_{p}\cap A_{q})$
is an interval. The convex hull of
![]() $A_{p}\cap A_{q}$
is a rectangle not contained on only one side of the line
$A_{p}\cap A_{q}$
is a rectangle not contained on only one side of the line
![]() $\{x=y\}.$
This implies that
$\{x=y\}.$
This implies that
 $P_{(-1/\sqrt {2},1/\sqrt {2})}(A_{p}\cap A_{q})$
contains
$P_{(-1/\sqrt {2},1/\sqrt {2})}(A_{p}\cap A_{q})$
contains
![]() $(0,0)$
as an interior point. Since the gap condition is preserved under linear perturbations close to the identity, as a result, we see that there is a non-trivial open set
$(0,0)$
as an interior point. Since the gap condition is preserved under linear perturbations close to the identity, as a result, we see that there is a non-trivial open set
![]() $O\subset S^{1}$
containing
$O\subset S^{1}$
containing
![]() $(-1/\sqrt {2},1/\sqrt {2})$
such that if
$(-1/\sqrt {2},1/\sqrt {2})$
such that if
![]() $v\in O,$
the linear projection
$v\in O,$
the linear projection
![]() $P_{v}(A_{p}\times A_{q})\subset \mathbb {R}v$
is an interval containing
$P_{v}(A_{p}\times A_{q})\subset \mathbb {R}v$
is an interval containing
![]() $(0,0).$
This implies that
$(0,0).$
This implies that
![]() $l_{v^{\perp }}\cap A_{p}\cap A_{q}\neq \emptyset .$
Thus we see that
$l_{v^{\perp }}\cap A_{p}\cap A_{q}\neq \emptyset .$
Thus we see that
![]() $\Pi _{(0,0)}(A_{p}\times A_{q})$
contains a non-empty interior around
$\Pi _{(0,0)}(A_{p}\times A_{q})$
contains a non-empty interior around
![]() $(1/\sqrt {2}),1/\sqrt {2})$
. We can now apply the same argument as in the proof of Theorem 2.2. For each integer
$(1/\sqrt {2}),1/\sqrt {2})$
. We can now apply the same argument as in the proof of Theorem 2.2. For each integer
![]() $k\geq 1,$
consider the line
$k\geq 1,$
consider the line
![]() $l_{k}$
passing through the origin with direction vector
$l_{k}$
passing through the origin with direction vector
![]() $(1,q^{\{k\log p/\log q\}}).$
If
$(1,q^{\{k\log p/\log q\}}).$
If
![]() $l_{k}\cap A_{p}\times A_{q}\neq \emptyset $
, then we find a point
$l_{k}\cap A_{p}\times A_{q}\neq \emptyset $
, then we find a point
![]() $(x,y)\in l_{k}\cap A_{p}\times A_{q}.$
Next, consider the point
$(x,y)\in l_{k}\cap A_{p}\times A_{q}.$
Next, consider the point
As before, we see that
 $$ \begin{align*} [x^{\prime}]=[y^{\prime}]\in N^{B_{p},B_{q}}_{p,q}. \end{align*} $$
$$ \begin{align*} [x^{\prime}]=[y^{\prime}]\in N^{B_{p},B_{q}}_{p,q}. \end{align*} $$
After replacing
![]() $A_{p}\times A_{q}$
with a suitable affine copy
$A_{p}\times A_{q}$
with a suitable affine copy
 $A^{\prime }_{p}\times A^{\prime }_{q}$
if necessary, as in the previous proof, we see that there is an interval
$A^{\prime }_{p}\times A^{\prime }_{q}$
if necessary, as in the previous proof, we see that there is an interval
![]() $I\subset [0,1]$
such that whenever
$I\subset [0,1]$
such that whenever
![]() $\{k \log p/ \log q\}\in I$
, there is a number
$\{k \log p/ \log q\}\in I$
, there is a number
 $n\in N^{B_{p},B_{q}}_{p,q}\cap [p^{k},p^{k+1}].$
Since
$n\in N^{B_{p},B_{q}}_{p,q}\cap [p^{k},p^{k+1}].$
Since
![]() $\{k \log p/\log q\}\in I$
happens for k inside a subset of integers with positive density, we see that there is a
$\{k \log p/\log q\}\in I$
happens for k inside a subset of integers with positive density, we see that there is a
![]() $c>0$
and for all large enough integers
$c>0$
and for all large enough integers
![]() $N,$
there are at least
$N,$
there are at least
![]() $cN$
many intervals among
$cN$
many intervals among
intersecting
 $N^{B_{p},B_{q}}_{p,q}.$
Thus the result follows by applying Kummer’s theorem (Theorem 1.3).
$N^{B_{p},B_{q}}_{p,q}.$
Thus the result follows by applying Kummer’s theorem (Theorem 1.3).
At this stage, Theorem 2.5 seems to be clear, at least under Schanuel’s conjecture. We will first prove this theorem under Schanuel’s conjecture and then explain how to get rid of it.
Proof of Theorem 2.5
Consider the set
 $N_{3}^{B_{3}}\times N_{4}^{B_{4}}\times N_{5}^{B_{5}}$
, where
$N_{3}^{B_{3}}\times N_{4}^{B_{4}}\times N_{5}^{B_{5}}$
, where
Now we construct the self-similar sets
By Lemma 3.6 (applied to suitable affine copies of
![]() $A_{3},A_{4},A_{5}$
), we see that
$A_{3},A_{4},A_{5}$
), we see that
![]() $S(A_{3})=1/2, S(A_{4})=1/3$
, and
$S(A_{3})=1/2, S(A_{4})=1/3$
, and
![]() $S(A_{5})=1/4.$
Thus we see that
$S(A_{5})=1/4.$
Thus we see that
 $$ \begin{align} S(A_{3})+S(A_{4})+S(A_{5})=\frac{13}{12}>1. \end{align} $$
$$ \begin{align} S(A_{3})+S(A_{4})+S(A_{5})=\frac{13}{12}>1. \end{align} $$
The convex hulls of
![]() $A_{3},A_{4},A_{5}$
are
$A_{3},A_{4},A_{5}$
are
![]() $[1/3,1/2],[1/4,1/3],[1/5,1/4].$
Let
$[1/3,1/2],[1/4,1/3],[1/5,1/4].$
Let
![]() $j_{1},j_{2}$
be integers. For the time being, we treat
$j_{1},j_{2}$
be integers. For the time being, we treat
![]() $j_{1}, j_{2}$
as being general. Later on, we will see that for the proof of this theorem, it is enough to choose
$j_{1}, j_{2}$
as being general. Later on, we will see that for the proof of this theorem, it is enough to choose
![]() $j_{1}=j_{2}=1.$
Let
$j_{1}=j_{2}=1.$
Let
![]() $k\geq 1$
be an integer and let
$k\geq 1$
be an integer and let
![]() $H_{j_{1},j_{2},k}$
be the plane
$H_{j_{1},j_{2},k}$
be the plane
Suppose that
![]() $H_{j_{1},j_{2},k}\cap A_{3}\times A_{4}\times A_{5}\neq \emptyset .$
We take a point
$H_{j_{1},j_{2},k}\cap A_{3}\times A_{4}\times A_{5}\neq \emptyset .$
We take a point
![]() $(x,y,z)$
in this intersection. Consider the point
$(x,y,z)$
in this intersection. Consider the point
Since we have
we see that
Thus we have
We assume Schanuel’s conjecture for the time being. Later on, we will remove this dependence.
From (3) and the discussion above Corollary 3.5, we claim that there exist
![]() $j_{1},j_{2}$
so that
$j_{1},j_{2}$
so that
![]() $H_{j_{1},j_{2},k}$
intersects
$H_{j_{1},j_{2},k}$
intersects
![]() $A_{3}\times A_{4}\times A_{5}$
for infinitely many integers
$A_{3}\times A_{4}\times A_{5}$
for infinitely many integers
![]() $k.$
More precisely, consider the plane
$k.$
More precisely, consider the plane
where
![]() $k_{1}\in [4^{j_{1}-1},4^{j_{1}}], k_{2}\in [5^{j_{2}-1},5^{j_{2}}]$
. It’s normal vector is
$k_{1}\in [4^{j_{1}-1},4^{j_{1}}], k_{2}\in [5^{j_{2}-1},5^{j_{2}}]$
. It’s normal vector is
![]() $(1,k_{1},-k_{2}).$
Then, as long as
$(1,k_{1},-k_{2}).$
Then, as long as
the Cartesian product of the convex hulls of
![]() $A_{3},A_{4},A_{5}$
intersects the plane
$A_{3},A_{4},A_{5}$
intersects the plane
![]() $H.$
In this case, we see that
$H.$
In this case, we see that
![]() $H\cap A_{3}\times A_{4}\times A_{5}$
is not empty if the minimal hull/maximal gap condition in Corollary 3.5 is satisfied. The lengths of the convex hulls of
$H\cap A_{3}\times A_{4}\times A_{5}$
is not empty if the minimal hull/maximal gap condition in Corollary 3.5 is satisfied. The lengths of the convex hulls of
![]() $A_{3},A_{4},A_{5}$
are
$A_{3},A_{4},A_{5}$
are
![]() $1/6,1/12,1/20.$
The lengths of the largest gaps are
$1/6,1/12,1/20.$
The lengths of the largest gaps are
![]() $1/18,1/24,3/100.$
The minimal hull/maximal gap condition can be now written as
$1/18,1/24,3/100.$
The minimal hull/maximal gap condition can be now written as
This is equivalent to the conditions
The region determined by (4), (6) is illustrated in Figure 1. From Figure 1, it is possible to see that
![]() $j_{1}=j_{2}=1$
will satisfy the claim. For later use, we write D for the set of pairs
$j_{1}=j_{2}=1$
will satisfy the claim. For later use, we write D for the set of pairs
![]() $(k_{1},k_{2})$
with conditions (4), (6), and
$(k_{1},k_{2})$
with conditions (4), (6), and
![]() $k_{1}\in [1,4],k_{2}\in [1,5].$
See the shaded region covered by vertical lines in Figure 2. Next, observe that the normal vector of
$k_{1}\in [1,4],k_{2}\in [1,5].$
See the shaded region covered by vertical lines in Figure 2. Next, observe that the normal vector of
![]() $H_{1,1,k}$
is
$H_{1,1,k}$
is
namely, in terms of
![]() $k_{1},k_{2}$
above,
$k_{1},k_{2}$
above,
By Schanuel’s conjecture, we see that the set
 $$ \begin{align*} \{(k\log 3/\log 4,k\log 3/\log 5)\ \mod \mathbb{Z}^{2}\}_{k\geq 1}\subset [0,1]^{2} \end{align*} $$
$$ \begin{align*} \{(k\log 3/\log 4,k\log 3/\log 5)\ \mod \mathbb{Z}^{2}\}_{k\geq 1}\subset [0,1]^{2} \end{align*} $$
is the orbit of an irrational rotation. Therefore, it is dense in
![]() $[0,1]^{2}.$
From here, we see that there are infinitely many k such that
$[0,1]^{2}.$
From here, we see that there are infinitely many k such that
![]() $(k_{1}(k),k_{2}(k))\in D.$
For such a
$(k_{1}(k),k_{2}(k))\in D.$
For such a
![]() $k,$
we have
$k,$
we have
![]() $H_{1,1,k}\cap A_{3}\times A_{4}\times A_{5}\neq \emptyset .$
This proves the claim with
$H_{1,1,k}\cap A_{3}\times A_{4}\times A_{5}\neq \emptyset .$
This proves the claim with
![]() $j_{1}=j_{2}=1.$
$j_{1}=j_{2}=1.$

Figure 2 The region
![]() ${\mathrm {Log}}(D)$
.
${\mathrm {Log}}(D)$
.
Now we know that there are infinitely many integers k so that
![]() $H_{1,1,k}\cap A_{3}\times A_{4}\times A_{5}\neq \emptyset .$
Now
$H_{1,1,k}\cap A_{3}\times A_{4}\times A_{5}\neq \emptyset .$
Now
![]() $x^{\prime },y^{\prime },z^{\prime }$
contains only
$x^{\prime },y^{\prime },z^{\prime }$
contains only
![]() $\{0,1\}$
in their
$\{0,1\}$
in their
![]() $3,4,5$
-ary expansions respectively. However, they might not be integers. If we take the integer parts, we see that
$3,4,5$
-ary expansions respectively. However, they might not be integers. If we take the integer parts, we see that
![]() $[x^{\prime }],[y^{\prime }],[z^{\prime }]$
contains only
$[x^{\prime }],[y^{\prime }],[z^{\prime }]$
contains only
![]() $\{0,1\}$
in their
$\{0,1\}$
in their
![]() $3,4,5$
-ary expansions respectively and
$3,4,5$
-ary expansions respectively and
The above equation tells us that
is an integer. Observe that
![]() $\{x^{\prime }\}, \{y^{\prime }\}, \{z^{\prime }\}$
are positive numbers whose
$\{x^{\prime }\}, \{y^{\prime }\}, \{z^{\prime }\}$
are positive numbers whose
![]() $3,4,5$
-ary expansions (respectively) contain only digits
$3,4,5$
-ary expansions (respectively) contain only digits
![]() $0$
and
$0$
and
![]() $1$
. Thus we see that
$1$
. Thus we see that
This implies that
 $$ \begin{align*} -\tfrac{5}{6}<\{z^{\prime}\}-\{x^{\prime}\}-\{y^{\prime}\}\leq \tfrac{1}{4}. \end{align*} $$
$$ \begin{align*} -\tfrac{5}{6}<\{z^{\prime}\}-\{x^{\prime}\}-\{y^{\prime}\}\leq \tfrac{1}{4}. \end{align*} $$
The only integer in this range is
![]() $0.$
Thus, we see that
$0.$
Thus, we see that
and
From here, the result follows from Schanuel’s conjecture.
Now, although we strongly do not believe it, it can be the case that
![]() $1$
,
$1$
,
![]() $\log 3/\log 4$
,
$\log 3/\log 4$
,
![]() $\log 3/\log 5$
are
$\log 3/\log 5$
are
![]() $\mathbb {Q}$
-dependent. Then the rotation on
$\mathbb {Q}$
-dependent. Then the rotation on
![]() $\mathbb {T}^{2}$
generated by the translation vector
$\mathbb {T}^{2}$
generated by the translation vector
![]() $(\log 3/\log 4, \log 3/\log 5)$
degenerates to an irrational rotation on a subtorus of dimension one. To be more precise, suppose that there are integers
$(\log 3/\log 4, \log 3/\log 5)$
degenerates to an irrational rotation on a subtorus of dimension one. To be more precise, suppose that there are integers
![]() $k_{1},k_{2},k_{3}$
such that
$k_{1},k_{2},k_{3}$
such that
 $$ \begin{align*} k_{1}\frac{\log 3}{\log 4}+k_{2}\frac{\log 3}{\log 5}+k_{3}=0. \end{align*} $$
$$ \begin{align*} k_{1}\frac{\log 3}{\log 4}+k_{2}\frac{\log 3}{\log 5}+k_{3}=0. \end{align*} $$
Neither
![]() $k_{1}$
nor
$k_{1}$
nor
![]() $k_{2}$
is zero. For example, suppose that
$k_{2}$
is zero. For example, suppose that
![]() $k_{1}=0,$
then this implies that
$k_{1}=0,$
then this implies that
![]() $1,\log 3,\log 5$
are not
$1,\log 3,\log 5$
are not
![]() $\mathbb {Q}$
-linearly independent, which is not possible. For convenience, we write
$\mathbb {Q}$
-linearly independent, which is not possible. For convenience, we write
![]() $a=\log 3/\log 4, b=\log 3/\log 5.$
We see that
$a=\log 3/\log 4, b=\log 3/\log 5.$
We see that
We can find non-zero coprime integers
![]() $l_{1},l_{2}$
such that
$l_{1},l_{2}$
such that
Here,
![]() $c\neq 0$
since otherwise
$c\neq 0$
since otherwise
![]() $\log 5/\log 4=a/b\in \mathbb {Q}$
, which is not the case. Since
$\log 5/\log 4=a/b\in \mathbb {Q}$
, which is not the case. Since
![]() $\gcd (l_{1},l_{2})=1$
, it is possible to find
$\gcd (l_{1},l_{2})=1$
, it is possible to find
![]() $S\in SL_{2}(\mathbb {Z})$
with entries
$S\in SL_{2}(\mathbb {Z})$
with entries
 $$ \begin{align*} S= \begin{pmatrix} l_{1} & l_{2} \\ l^{\prime}_{1} & l^{\prime}_{2} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} S= \begin{pmatrix} l_{1} & l_{2} \\ l^{\prime}_{1} & l^{\prime}_{2} \end{pmatrix}. \end{align*} $$
Thus, S is a well-defined invertible map
![]() $\mathbb {T}^{2}\to \mathbb {T}^{2}.$
Let k be an integer and consider the point
$\mathbb {T}^{2}\to \mathbb {T}^{2}.$
Let k be an integer and consider the point
![]() $(ka,kb)\in \mathbb {T}^{2}.$
Now, we see that
$(ka,kb)\in \mathbb {T}^{2}.$
Now, we see that
 $$ \begin{align*} S(ka,kb)&=(l_{1}ka+l_{2}kb,l^{\prime}_{1}ka+l^{\prime}_{2}kb)\ \mod \mathbb{Z}^{2}\\ &= (kc,k(l^{\prime}_{1}a+l^{\prime}_{2}b))\ \mod \mathbb{Z}^{2}. \end{align*} $$
$$ \begin{align*} S(ka,kb)&=(l_{1}ka+l_{2}kb,l^{\prime}_{1}ka+l^{\prime}_{2}kb)\ \mod \mathbb{Z}^{2}\\ &= (kc,k(l^{\prime}_{1}a+l^{\prime}_{2}b))\ \mod \mathbb{Z}^{2}. \end{align*} $$
It is simple to check that
![]() $l^{\prime }_{1}a+l^{\prime }_{2}b\notin \mathbb {Q}$
for otherwise, both
$l^{\prime }_{1}a+l^{\prime }_{2}b\notin \mathbb {Q}$
for otherwise, both
![]() $a,b$
are rational, which is impossible.
$a,b$
are rational, which is impossible.
We identify
![]() $\mathbb {T}^{2}$
with
$\mathbb {T}^{2}$
with
![]() $[0,1]^{2}$
by letting
$[0,1]^{2}$
by letting
be the unique point
![]() $(x^{\prime },y^{\prime })\in [0,1)^{2}$
such that
$(x^{\prime },y^{\prime })\in [0,1)^{2}$
such that
![]() $(x^{\prime },y^{\prime })-(x,y)\in \mathbb {Z}^{2}.$
Under this identification, the closure
$(x^{\prime },y^{\prime })-(x,y)\in \mathbb {Z}^{2}.$
Under this identification, the closure
![]() $\overline {\{S(ka,kb)\}_{k\geq 0}}$
is a union of vertical line segments in
$\overline {\{S(ka,kb)\}_{k\geq 0}}$
is a union of vertical line segments in
![]() $[0,1]^{2}$
. In particular, it contains the vertical line
$[0,1]^{2}$
. In particular, it contains the vertical line
![]() $\{x=0\}\cap [0,1]^{2}.$
Performing
$\{x=0\}\cap [0,1]^{2}.$
Performing
![]() $S^{-1},$
we see that
$S^{-1},$
we see that
![]() $\overline {\{(ka,kb)\}_{k\geq 0}}$
contains the line
$\overline {\{(ka,kb)\}_{k\geq 0}}$
contains the line
Although, in general,
![]() $L_{0}$
is a union of line segments in
$L_{0}$
is a union of line segments in
![]() $[0,1]^{2}$
, we will call it to be a line. In fact, it is actually a line in
$[0,1]^{2}$
, we will call it to be a line. In fact, it is actually a line in
![]() $\mathbb {T}^{2}.$
Since
$\mathbb {T}^{2}.$
Since
![]() $c\neq 0,$
we write
$c\neq 0,$
we write
![]() $c=p/q$
or
$c=p/q$
or
![]() $c=-p/q$
with positive integers
$c=-p/q$
with positive integers
![]() $p,q$
so that
$p,q$
so that
![]() $\gcd (p,q)=1.$
Then, with similar arguments as above, we see that
$\gcd (p,q)=1.$
Then, with similar arguments as above, we see that
![]() $\overline {\{(ka,kb)\}_{k\geq 0}}$
also contains
$\overline {\{(ka,kb)\}_{k\geq 0}}$
also contains
for
![]() $t\in \{1/q,2/q,\ldots ,(q-1)/q\}.$
$t\in \{1/q,2/q,\ldots ,(q-1)/q\}.$
Next, we use our knowledge of the set D in Figure 1. We want to choose an integer k such that
The closure of
![]() $V_{k},k\geq 1$
is a union of curves. After performing the logarithmic map
$V_{k},k\geq 1$
is a union of curves. After performing the logarithmic map
![]() $\mathrm {Log}:(x,y)\to (1-\log x/\log 4,1-\log y/\log 5)$
, those curves become line segments. As we discussed above,
$\mathrm {Log}:(x,y)\to (1-\log x/\log 4,1-\log y/\log 5)$
, those curves become line segments. As we discussed above,
![]() $\overline {\{V_{k}\}_{k\geq 1}}$
contains the line
$\overline {\{V_{k}\}_{k\geq 1}}$
contains the line
![]() $L_{0}.$
$L_{0}.$
Recall that neither
![]() $l_{1}$
nor
$l_{1}$
nor
![]() $l_{2}$
is zero. To find
$l_{2}$
is zero. To find
![]() $V_{k}\in D,$
it is enough to find k so that
$V_{k}\in D,$
it is enough to find k so that
To do this, it is enough to show that at least one of the lines
intersect the interior of
![]() ${\mathrm {Log}}(D).$
If this is done, then we can find infinitely many k so that
${\mathrm {Log}}(D).$
If this is done, then we can find infinitely many k so that
![]() $V_{k}\in D.$
The region
$V_{k}\in D.$
The region
![]() ${\mathrm {Log}}(D)$
is illustrated in Figure 2.
${\mathrm {Log}}(D)$
is illustrated in Figure 2.
In order that the line
![]() $L_{0}$
avoids
$L_{0}$
avoids
![]() ${\mathrm {Log}}(D)$
, both
${\mathrm {Log}}(D)$
, both
![]() $l_{1},l_{2}$
cannot be too large. First,
$l_{1},l_{2}$
cannot be too large. First,
![]() ${\mathrm {Log}}(D)\cap \{y=0\}$
has length bigger than
${\mathrm {Log}}(D)\cap \{y=0\}$
has length bigger than
![]() $0.5.$
Since
$0.5.$
Since
![]() $L_{0}$
contains points
$L_{0}$
contains points
![]() $(0,1),(1/\lvert l_{1}\rvert ,1),\ldots , ((\lvert l_{1}\rvert -1)/\lvert l_{1}\rvert ,1),(1,1),$
we see that
$(0,1),(1/\lvert l_{1}\rvert ,1),\ldots , ((\lvert l_{1}\rvert -1)/\lvert l_{1}\rvert ,1),(1,1),$
we see that
![]() $\lvert l_{1}\rvert <2.$
Therefore,
$\lvert l_{1}\rvert <2.$
Therefore,
![]() $l_{1}=\pm 1.$
Without loss of generality, we can assume that
$l_{1}=\pm 1.$
Without loss of generality, we can assume that
![]() $l_{1}=1.$
Then we can consider possible values for
$l_{1}=1.$
Then we can consider possible values for
![]() $l_{2}.$
We see that
$l_{2}.$
We see that
![]() $l_{2}<0$
. Otherwise if
$l_{2}<0$
. Otherwise if
![]() $l_{2}>0, L_{0}$
must contain a line segment starting from
$l_{2}>0, L_{0}$
must contain a line segment starting from
![]() $(1,0)$
to the boundary
$(1,0)$
to the boundary
![]() $\{x=0\}$
and this line segment must intersect the interior of
$\{x=0\}$
and this line segment must intersect the interior of
![]() ${\mathrm {Log}}(D)$
unless it is horizontal, which is not possible. Similarly, as long as
${\mathrm {Log}}(D)$
unless it is horizontal, which is not possible. Similarly, as long as
![]() $l_{2}\leq -3, L_{0}$
contains a line segment starting from a point
$l_{2}\leq -3, L_{0}$
contains a line segment starting from a point
![]() $(1,r), r\in [0,1/3]$
to the boundary
$(1,r), r\in [0,1/3]$
to the boundary
![]() $\{x=0\}$
and this line segment must intersect the interior of
$\{x=0\}$
and this line segment must intersect the interior of
![]() ${\mathrm {Log}}(D).$
Thus we see that all possible values for
${\mathrm {Log}}(D).$
Thus we see that all possible values for
![]() $l_{2}$
are
$l_{2}$
are
![]() $-1,-2.$
$-1,-2.$
Now, we consider all possible values for
![]() $c=p/q.$
We see that
$c=p/q.$
We see that
![]() $(t,0)\in L_{t}$
for
$(t,0)\in L_{t}$
for
![]() $t\in \{1/q,\ldots ,(q-1)/q\}.$
Then with a similar argument as above, we see that
$t\in \{1/q,\ldots ,(q-1)/q\}.$
Then with a similar argument as above, we see that
![]() $q< 2.$
Therefore,
$q< 2.$
Therefore,
![]() $q=1.$
This implies that
$q=1.$
This implies that
![]() $c\in \mathbb {Z}.$
$c\in \mathbb {Z}.$
In conclusion, in order that
![]() $V_{k}\in D$
for at most finitely many integers
$V_{k}\in D$
for at most finitely many integers
![]() $k,$
we must have
$k,$
we must have
for
![]() $l_{1}=1,l_{2}=-1 \text { or } -2.$
It can be checked directly that
$l_{1}=1,l_{2}=-1 \text { or } -2.$
It can be checked directly that
 $$ \begin{align*} \frac{\log 3}{\log 4}-\frac{\log 3}{\log 5}=0.109875+e_{1}, \end{align*} $$
$$ \begin{align*} \frac{\log 3}{\log 4}-\frac{\log 3}{\log 5}=0.109875+e_{1}, \end{align*} $$
 $$ \begin{align*} \frac{\log 3}{\log 4}-2\frac{\log 3}{\log 5}=-0.572731+e_{2}, \end{align*} $$
$$ \begin{align*} \frac{\log 3}{\log 4}-2\frac{\log 3}{\log 5}=-0.572731+e_{2}, \end{align*} $$
where
![]() $\lvert e_{1}\rvert , \lvert e_{2}\rvert <0.001$
. Thus, the numbers on the left-hand side above are not integers. From here, the proof is finished.
$\lvert e_{1}\rvert , \lvert e_{2}\rvert <0.001$
. Thus, the numbers on the left-hand side above are not integers. From here, the proof is finished.
We discuss more on Theorem 2.5. First, we remark that with the same proof, one can also show that the conclusion holds with
![]() $(3,4,5)$
being replaced with
$(3,4,5)$
being replaced with
![]() $(3,4,7).$
More generally, let
$(3,4,7).$
More generally, let
![]() $l\geq 1$
be an integer. Let
$l\geq 1$
be an integer. Let
![]() $D=\{0,\ldots ,l\}.$
We want to consider the set (
$D=\{0,\ldots ,l\}.$
We want to consider the set (
 $N^{D}_{b_{1}}+N^{D}_{b_{2}})\cap N^{D}_{b_{3}}$
for
$N^{D}_{b_{1}}+N^{D}_{b_{2}})\cap N^{D}_{b_{3}}$
for
![]() $b_{1},b_{2},b_{3}\geq l+1.$
In this case, under Schanuel’s conjecture, it is possible to show that
$b_{1},b_{2},b_{3}\geq l+1.$
In this case, under Schanuel’s conjecture, it is possible to show that
 $$ \begin{align*}(N^{D}_{b_{1}}+N^{D}_{b_{2}})\cap N^{D}_{b_{3}}\end{align*} $$
$$ \begin{align*}(N^{D}_{b_{1}}+N^{D}_{b_{2}})\cap N^{D}_{b_{3}}\end{align*} $$
is infinite as long as
 $$ \begin{align*} \frac{l}{b_{1}-1}+\frac{l}{b_{2}-1}+\frac{l}{b_{3}-1}\geq 1, \end{align*} $$
$$ \begin{align*} \frac{l}{b_{1}-1}+\frac{l}{b_{2}-1}+\frac{l}{b_{3}-1}\geq 1, \end{align*} $$
and
![]() $1,\log b_{1},\log b_{2},\log b_{3}$
are
$1,\log b_{1},\log b_{2},\log b_{3}$
are
![]() $\mathbb {Q}$
-linearly independent. Again, for specific cases, Schanuel’s conjecture may not be required. For example, when
$\mathbb {Q}$
-linearly independent. Again, for specific cases, Schanuel’s conjecture may not be required. For example, when
![]() $l=2,$
it is possible to check that the above statement holds for
$l=2,$
it is possible to check that the above statement holds for
![]() $(b_{1},b_{2},b_{3})=(4,5,6).$
$(b_{1},b_{2},b_{3})=(4,5,6).$
Lastly, we are going to prove Theorem 2.7. Before that, we first show the following results.
Lemma 5.1. Let
![]() $b\geq 3$
be an integer and let
$b\geq 3$
be an integer and let
![]() $B=\{1,2,\ldots ,b-1\}.$
Consider the set
$B=\{1,2,\ldots ,b-1\}.$
Consider the set
 $$ \begin{align*} A^{B}_{b}=\{x\in [0,1]: \text{ some }{b}\text{-ary expansion of }{x}\text{ contains only digits in }B \}. \end{align*} $$
$$ \begin{align*} A^{B}_{b}=\{x\in [0,1]: \text{ some }{b}\text{-ary expansion of }{x}\text{ contains only digits in }B \}. \end{align*} $$
Then we have
 $S(A^{B}_{b})=(b-2)/(b-1).$
Moreover, let
$S(A^{B}_{b})=(b-2)/(b-1).$
Moreover, let
![]() $k\in \{0,1,\ldots ,b-2\}$
. Consider the set
$k\in \{0,1,\ldots ,b-2\}$
. Consider the set
 $$ \begin{align*} \tilde{A}^{B}_{b}=A^{B}_{b}\cap [0,(b-k)/b]. \end{align*} $$
$$ \begin{align*} \tilde{A}^{B}_{b}=A^{B}_{b}\cap [0,(b-k)/b]. \end{align*} $$
Then,
 $S(\tilde {A}^{B}_{b})=S(A^{B}_{b}).$
$S(\tilde {A}^{B}_{b})=S(A^{B}_{b}).$
Remark 5.2. The second conclusion is special for our self-similar set
 $A^{B}_{b}.$
We need to cut
$A^{B}_{b}.$
We need to cut
 $A^{B}_{b}$
at the ‘right places’. For general Cantor sets, cutting out a small portion may decrease the thickness dramatically.
$A^{B}_{b}$
at the ‘right places’. For general Cantor sets, cutting out a small portion may decrease the thickness dramatically.
Proof. The first conclusion follows from Lemma 3.6. Indeed, by applying the symmetry
![]() $x\in \mathbb {R}\to -x\in \mathbb {R}$
to the set
$x\in \mathbb {R}\to -x\in \mathbb {R}$
to the set
 $A^{B}_{b},$
we obtain a set for which Lemma 3.6 can be used.
$A^{B}_{b},$
we obtain a set for which Lemma 3.6 can be used.
For the second conclusion, we can use the self-similarity of
 $A^{B}_{b}.$
First, let
$A^{B}_{b}.$
First, let
![]() $[a,1]$
be the convex hull of
$[a,1]$
be the convex hull of
 $A^{B}_{b}$
(this determines the value for
$A^{B}_{b}$
(this determines the value for
![]() $a\in (0,1/b)$
). Then we see that
$a\in (0,1/b)$
). Then we see that
![]() $[a,(b-k)/b]$
is the convex hull of
$[a,(b-k)/b]$
is the convex hull of
 $\tilde {A}^{B}_{b}$
. Observe that
$\tilde {A}^{B}_{b}$
. Observe that
 $A^{B}_{b}\cap [1/b,2/b],\ldots ,A^{B}_{b}\cap [(b-k-1)/b,(b-k)/b]$
are translated copies of each other. The largest gaps of
$A^{B}_{b}\cap [1/b,2/b],\ldots ,A^{B}_{b}\cap [(b-k-1)/b,(b-k)/b]$
are translated copies of each other. The largest gaps of
 $\tilde {A}^{B}_{b}$
are located inside each of those copies. From here, we see that
$\tilde {A}^{B}_{b}$
are located inside each of those copies. From here, we see that
 $$ \begin{align*} S(\tilde{A}^{B}_{b})=(b-2)/(b-1).\\[-3.1pc] \end{align*} $$
$$ \begin{align*} S(\tilde{A}^{B}_{b})=(b-2)/(b-1).\\[-3.1pc] \end{align*} $$
Lemma 5.3. Let
![]() $\delta _{1},\delta _{2}\in (0,1)$
numbers so that
$\delta _{1},\delta _{2}\in (0,1)$
numbers so that
![]() $\delta _{1}<\delta _{2}.$
Let
$\delta _{1}<\delta _{2}.$
Let
![]() $C\subset [0,1]$
be a Cantor set with
$C\subset [0,1]$
be a Cantor set with
![]() $\mathrm{Conv(C)}\neq [0,1], S(C)>1-\delta _{1}$
, and
$\mathrm{Conv(C)}\neq [0,1], S(C)>1-\delta _{1}$
, and
![]() $\lvert \mathrm{Conv(C)}\rvert>1-\delta _{1}.$
Consider the set
$\lvert \mathrm{Conv(C)}\rvert>1-\delta _{1}.$
Consider the set
 $A_{b}^{B}$
as in Lemma 5.1. Then for each
$A_{b}^{B}$
as in Lemma 5.1. Then for each
![]() $\delta _{2}\in (0,1),$
as long as
$\delta _{2}\in (0,1),$
as long as
![]() $\delta _{1}$
is small enough, for all sufficiently large
$\delta _{1}$
is small enough, for all sufficiently large
![]() $b>1,$
there is a compact set
$b>1,$
there is a compact set
 $C^{\prime }\subset C\cap A_{b}^{B}$
satisfying
$C^{\prime }\subset C\cap A_{b}^{B}$
satisfying
 $$ \begin{align*} \lvert \mathrm{Conv(C^{\prime})}\rvert &> 1-\delta_{2},\\ S(C^{\prime}) &>1-\delta_{2}. \end{align*} $$
$$ \begin{align*} \lvert \mathrm{Conv(C^{\prime})}\rvert &> 1-\delta_{2},\\ S(C^{\prime}) &>1-\delta_{2}. \end{align*} $$
Moreover, there is a number
![]() $c>0$
such that for linear maps
$c>0$
such that for linear maps
![]() $T:x\to rx+t, T^{\prime }:x\to r^{\prime }x+t^{\prime }$
with
$T:x\to rx+t, T^{\prime }:x\to r^{\prime }x+t^{\prime }$
with
![]() $r,r^{\prime }\in (1-c,1+c)$
and
$r,r^{\prime }\in (1-c,1+c)$
and
![]() $t,t^{\prime }\in (-c,c),$
there is a compact set
$t,t^{\prime }\in (-c,c),$
there is a compact set
 $C^{\prime }\subset T(C)\cap T^{\prime }(A_{b}^{B})\cap [0,1]$
satisfying the above properties as well.
$C^{\prime }\subset T(C)\cap T^{\prime }(A_{b}^{B})\cap [0,1]$
satisfying the above properties as well.
Proof. We want to use Theorem 3.3. The issue is that
 $\mathrm{Conv(C)}\cap \mathrm{Conv(A_{b}^{B})}$
may contain C or
$\mathrm{Conv(C)}\cap \mathrm{Conv(A_{b}^{B})}$
may contain C or
 $A_{b}^{B}.$
Observe that
$A_{b}^{B}.$
Observe that
 $\mathrm{Conv(A_{b}^{B})}=[a_{b},1]$
with
$\mathrm{Conv(A_{b}^{B})}=[a_{b},1]$
with
![]() $\lim _{b\to \infty } a_{b}\to 0$
, and that
$\lim _{b\to \infty } a_{b}\to 0$
, and that
 $\lim _{b\to \infty } S(A_{b}^{B})\to 1.$
So as long as b is large enough,
$\lim _{b\to \infty } S(A_{b}^{B})\to 1.$
So as long as b is large enough,
 $C, A_{b}^{B}$
are not contained in each other’s gaps. Let
$C, A_{b}^{B}$
are not contained in each other’s gaps. Let
![]() $\mathrm{Conv(C)}=[c,d]\subset [0,1].$
$\mathrm{Conv(C)}=[c,d]\subset [0,1].$
If
![]() $c=0,$
then
$c=0,$
then
![]() $d<1$
and we see that
$d<1$
and we see that
 $\mathrm{Conv(C)}\cap \mathrm{Conv(A_{b}^{B})}$
contains neither C nor
$\mathrm{Conv(C)}\cap \mathrm{Conv(A_{b}^{B})}$
contains neither C nor
 $A_{b}^{B}.$
Using Theorem 3.3, we conclude that as long as
$A_{b}^{B}.$
Using Theorem 3.3, we conclude that as long as
![]() $\delta _{1}$
is small enough and b is large enough, there is a compact set
$\delta _{1}$
is small enough and b is large enough, there is a compact set
 $C^{\prime }\subset C\cap A^{B}_{b}$
such that
$C^{\prime }\subset C\cap A^{B}_{b}$
such that
are both greater than
![]() $1-\delta _{2}.$
$1-\delta _{2}.$
If
![]() $c>0,$
by making b sufficiently large, we can then assume that
$c>0,$
by making b sufficiently large, we can then assume that
![]() $a_{b}<c.$
As
$a_{b}<c.$
As
![]() $\lvert \mathrm{Conv(C)}\rvert>1-\delta _{1}$
, we see that
$\lvert \mathrm{Conv(C)}\rvert>1-\delta _{1}$
, we see that
![]() $d> 1-\delta _{1}.$
Let k be the smallest integer with
$d> 1-\delta _{1}.$
Let k be the smallest integer with
![]() $(b-k)/b< d.$
Consider the set
$(b-k)/b< d.$
Consider the set
 $\tilde {A}_{b}^{B}$
as in Lemma 5.1. We see that
$\tilde {A}_{b}^{B}$
as in Lemma 5.1. We see that
 $$ \begin{align*} \lvert \mathrm{Conv}(\tilde{\mathrm{A}}_{\mathrm{b}}^{\mathrm{B}})\rvert =\frac{b-k}{b}-a_{b}>1-\delta_{1}-\frac{1}{b}-a_{b}. \end{align*} $$
$$ \begin{align*} \lvert \mathrm{Conv}(\tilde{\mathrm{A}}_{\mathrm{b}}^{\mathrm{B}})\rvert =\frac{b-k}{b}-a_{b}>1-\delta_{1}-\frac{1}{b}-a_{b}. \end{align*} $$
This number can be made arbitrarily close to
![]() $1-\delta _{1}$
by making b sufficiently large (in a manner that depends on
$1-\delta _{1}$
by making b sufficiently large (in a manner that depends on
![]() $\delta _{1}$
). Now since
$\delta _{1}$
). Now since
 $\mathrm{Conv(C)}\cap \mathrm{Conv}(\tilde {\mathrm{A}}_{\mathrm{b}}^{\mathrm{B}})$
contains neither C nor
$\mathrm{Conv(C)}\cap \mathrm{Conv}(\tilde {\mathrm{A}}_{\mathrm{b}}^{\mathrm{B}})$
contains neither C nor
 $\tilde {A}_{b}^{B},$
by Theorem 3.3, we see that (for small enough
$\tilde {A}_{b}^{B},$
by Theorem 3.3, we see that (for small enough
![]() $\delta _{1}$
and large enough b) there is a compact set
$\delta _{1}$
and large enough b) there is a compact set
 $C^{\prime }\subset C\cap \tilde {A}^{B}_{b}\subset C\cap A^{B}_{b}$
such that
$C^{\prime }\subset C\cap \tilde {A}^{B}_{b}\subset C\cap A^{B}_{b}$
such that
are both greater than
![]() $1-\delta _{2}.$
$1-\delta _{2}.$
For the second conclusion, notice that if
 $\mathrm{Conv(C)}\cap \mathrm{Conv(A_{b}^{B})}$
does not contain
$\mathrm{Conv(C)}\cap \mathrm{Conv(A_{b}^{B})}$
does not contain
 $C, A_{b}^{B},$
then as long as c is small enough,
$C, A_{b}^{B},$
then as long as c is small enough,
 $\mathrm{Conv(T(C))}\cap \mathrm{Conv(T^{\prime }(A_{b}^{B}))}$
does not contain
$\mathrm{Conv(T(C))}\cap \mathrm{Conv(T^{\prime }(A_{b}^{B}))}$
does not contain
 $T(C), T^{\prime }(A_{b}^{B}).$
The same conclusion holds with
$T(C), T^{\prime }(A_{b}^{B}).$
The same conclusion holds with
 $A_{b}^{B}$
being replaced with
$A_{b}^{B}$
being replaced with
 $\tilde {A}_{b}^{B}$
. Thus it is possible to find a compact subset
$\tilde {A}_{b}^{B}$
. Thus it is possible to find a compact subset
 $C^{\prime }\subset T(C)\cap T^{\prime }(A_{b}^{B})$
satisfying the desired properties. However, later on, it is more convenient to consider
$C^{\prime }\subset T(C)\cap T^{\prime }(A_{b}^{B})$
satisfying the desired properties. However, later on, it is more convenient to consider
 $T(C)\cap T^{\prime }(A_{b}^{B})\cap [0,1].$
We cannot simply take
$T(C)\cap T^{\prime }(A_{b}^{B})\cap [0,1].$
We cannot simply take
![]() $C^{\prime }\cap [0,1]$
as the thickness can decrease significantly. Instead, we consider the set
$C^{\prime }\cap [0,1]$
as the thickness can decrease significantly. Instead, we consider the set
 $T^{\prime }(A_{b}^{B})\cap [0,1].$
The set
$T^{\prime }(A_{b}^{B})\cap [0,1].$
The set
 $T^{\prime }(A_{b}^{B})$
is a self-similar set. The scaling ratio is still
$T^{\prime }(A_{b}^{B})$
is a self-similar set. The scaling ratio is still
![]() $1/b.$
The first level branches are intervals of length
$1/b.$
The first level branches are intervals of length
![]() $r^{\prime }/b.$
It can happen that some of the first level branches are not contained in
$r^{\prime }/b.$
It can happen that some of the first level branches are not contained in
![]() $[0,1].$
If this is the case, we simply ignore them. We can choose c to be so small that we only need to ignore at most one first level branch. As a result, as long as c is small enough, we obtain a subset
$[0,1].$
If this is the case, we simply ignore them. We can choose c to be so small that we only need to ignore at most one first level branch. As a result, as long as c is small enough, we obtain a subset
 $\tilde {\tilde {A}}_{b}^{B}\subset T^{\prime }(A_{b}^{B})\cap [0,1]$
whose thickness is the same as
$\tilde {\tilde {A}}_{b}^{B}\subset T^{\prime }(A_{b}^{B})\cap [0,1]$
whose thickness is the same as
 $A_{b}^{B}$
and whose diameter is at least
$A_{b}^{B}$
and whose diameter is at least
![]() $1-3r^{\prime }/b$
. We can then consider the intersection between
$1-3r^{\prime }/b$
. We can then consider the intersection between
![]() $T(C)$
and
$T(C)$
and
 $\tilde {\tilde {A}}_{b}^{B}$
as in the case when
$\tilde {\tilde {A}}_{b}^{B}$
as in the case when
![]() $T,T^{\prime }$
are the identity map. From here, the result follows.
$T,T^{\prime }$
are the identity map. From here, the result follows.
Proof of Theorem 2.7
Let
![]() $3\leq b_{1}\leq \cdots \leq b_{k}$
be (not necessarily distinct) integers. We need them to be sufficiently large in a manner that will be discussed later in the proof.
$3\leq b_{1}\leq \cdots \leq b_{k}$
be (not necessarily distinct) integers. We need them to be sufficiently large in a manner that will be discussed later in the proof.
For each
![]() $i\in \{1,\ldots ,k\}$
, we construct the set
$i\in \{1,\ldots ,k\}$
, we construct the set
If x has two possible
![]() $b_{i}$
-ary expansions, we will take the finite expansion. Thus the
$b_{i}$
-ary expansions, we will take the finite expansion. Thus the
![]() $b_{i}$
-ary expansion for
$b_{i}$
-ary expansion for
![]() $x>0$
is well defined. It is sufficient to consider the set
$x>0$
is well defined. It is sufficient to consider the set
We claim that it is enough to prove that A is unbounded. Indeed, if A is unbounded, then we can find arbitrarily large x whose base
![]() $b_{1},\ldots ,b_{k}$
expansions do not have digit zero. We simply take the integer part of x to obtain an integer
$b_{1},\ldots ,b_{k}$
expansions do not have digit zero. We simply take the integer part of x to obtain an integer
![]() $[x]$
whose base
$[x]$
whose base
![]() $b_{1},\ldots ,b_{k}$
expansions do not have digit zero. Since A is unbounded, the proof finishes.
$b_{1},\ldots ,b_{k}$
expansions do not have digit zero. Since A is unbounded, the proof finishes.
Now it is enough to prove that A is unbounded. We define the integer sequence
by starting with
For
![]() $j\geq 1,$
define
$j\geq 1,$
define
![]() $a_{1,j}=b_{1}a_{1,j-1}.$
For
$a_{1,j}=b_{1}a_{1,j-1}.$
For
![]() $i\in \{2,\ldots ,k\},$
we define
$i\in \{2,\ldots ,k\},$
we define
![]() $a_{i,j}=b_{i}a_{i,j-1}$
if
$a_{i,j}=b_{i}a_{i,j-1}$
if
 $a_{i,j-1}/a_{1,j}<b^{-1}_{i}$
and
$a_{i,j-1}/a_{1,j}<b^{-1}_{i}$
and
![]() $a_{i,j}=a_{i,j-1}$
otherwise. In this way, we have
$a_{i,j}=a_{i,j-1}$
otherwise. In this way, we have
 $$ \begin{align*} \mathbf{a}_{j}=(b^{j}_{1},b^{[j\log_{b_{2}} b_{1}]}_{2},\ldots,b^{[j\log_{b_{k}} b_{1}]}_{k})=b^{j}_{1}(1,b^{-\{j\log {}_{b_{2}} b_{1}\}}_{2},\ldots,b^{-\{j\log {}_{b_{k}} b_{1}\}}_{k}). \end{align*} $$
$$ \begin{align*} \mathbf{a}_{j}=(b^{j}_{1},b^{[j\log_{b_{2}} b_{1}]}_{2},\ldots,b^{[j\log_{b_{k}} b_{1}]}_{k})=b^{j}_{1}(1,b^{-\{j\log {}_{b_{2}} b_{1}\}}_{2},\ldots,b^{-\{j\log {}_{b_{k}} b_{1}\}}_{k}). \end{align*} $$
The rotation on
![]() $\mathbb {T}^{k-1}$
with the rotation angle
$\mathbb {T}^{k-1}$
with the rotation angle
 $$ \begin{align*} v=\bigg(\frac{\log b_{1}}{\log b_{2}},\ldots,\frac{\log b_{1}}{\log b_{k}}\bigg) \end{align*} $$
$$ \begin{align*} v=\bigg(\frac{\log b_{1}}{\log b_{2}},\ldots,\frac{\log b_{1}}{\log b_{k}}\bigg) \end{align*} $$
may not be an irrational rotation on
![]() $\mathbb {T}^{k-1}$
. Nonetheless, we claim that the orbit
$\mathbb {T}^{k-1}$
. Nonetheless, we claim that the orbit
can be close to the origin, that is,
![]() $d(nv,\mathbb {Z}^{k-1})$
can be arbitrarily small. In fact,
$d(nv,\mathbb {Z}^{k-1})$
can be arbitrarily small. In fact,
 $\overline {\{nv\ \mod \mathbb {Z}^{k-1}\}_{k\geq 0}}$
is a set of form
$\overline {\{nv\ \mod \mathbb {Z}^{k-1}\}_{k\geq 0}}$
is a set of form
![]() ${T^{\prime }}+P$
, where
${T^{\prime }}+P$
, where
![]() $T^{\prime }$
is a (possibly trivial) subtorus and P is a finite set of rational points containing
$T^{\prime }$
is a (possibly trivial) subtorus and P is a finite set of rational points containing
![]() $(0,\ldots ,0)$
. It is possible that
$(0,\ldots ,0)$
. It is possible that
![]() $T^{\prime }$
is a singleton in which case,
$T^{\prime }$
is a singleton in which case,
![]() $nv\ \mod \mathbb {Z}^{k-1}$
is periodic. In any case,
$nv\ \mod \mathbb {Z}^{k-1}$
is periodic. In any case,
![]() $T^{\prime }$
contains the origin and this proves the claim.
$T^{\prime }$
contains the origin and this proves the claim.
Let
![]() $\delta ^{\prime }\in (0,1/2).$
Let
$\delta ^{\prime }\in (0,1/2).$
Let
![]() $\epsilon>0$
be a small number such that
$\epsilon>0$
be a small number such that
Notice that there are infinitely many n such that
![]() $d(nv,\mathbb {Z}^{k-1})<\epsilon .$
Let n be such an integer. Then we see that
$d(nv,\mathbb {Z}^{k-1})<\epsilon .$
Let n be such an integer. Then we see that
where
![]() $v_{i}\in (1-\delta ^{\prime },1].$
For each
$v_{i}\in (1-\delta ^{\prime },1].$
For each
![]() $i\in \{1,2,\ldots ,k\}$
, let
$i\in \{1,2,\ldots ,k\}$
, let
We claim that if
![]() $b_{1},b_{2},\ldots ,b_{k}$
are sufficiently large, then
$b_{1},b_{2},\ldots ,b_{k}$
are sufficiently large, then
![]() $B_{1,n}\cap B_{2,n}\cap \cdots \cap B_{k,n}\neq \emptyset .$
The most convenient way to look at this is to rescale the whole situation by a factor of
$B_{1,n}\cap B_{2,n}\cap \cdots \cap B_{k,n}\neq \emptyset .$
The most convenient way to look at this is to rescale the whole situation by a factor of
![]() $b^{-n}_{1}.$
After doing this,
$b^{-n}_{1}.$
After doing this,
![]() $B_{1,n}$
fits to the interval
$B_{1,n}$
fits to the interval
![]() $[1,b_{1}]$
while
$[1,b_{1}]$
while
![]() $B_{2,n},\ldots , B_{k,n}$
fit to the intervals
$B_{2,n},\ldots , B_{k,n}$
fit to the intervals
![]() $[v_{2},b_{2}v_{2}],\ldots , [v_{k},b_{k}v_{k}].$
As one can choose
$[v_{2},b_{2}v_{2}],\ldots , [v_{k},b_{k}v_{k}].$
As one can choose
![]() $\delta ^{\prime }$
to be arbitrarily small,
$\delta ^{\prime }$
to be arbitrarily small,
![]() $v_{1},v_{2},\ldots ,v_{k}$
can be arbitrarily close to one. It is enough to consider the situation with
$v_{1},v_{2},\ldots ,v_{k}$
can be arbitrarily close to one. It is enough to consider the situation with
![]() $1=v_{1}=v_{2}=v_{3}=\cdots =v_{k}.$
Indeed, both the thickness and the gap conditions in Theorems 3.2, 3.3 are preserved if one rescales and translates each Cantor set slightly. We will come back to this point shortly. If
$1=v_{1}=v_{2}=v_{3}=\cdots =v_{k}.$
Indeed, both the thickness and the gap conditions in Theorems 3.2, 3.3 are preserved if one rescales and translates each Cantor set slightly. We will come back to this point shortly. If
![]() $v_{1},v_{2},\ldots , v_{k}$
are exactly
$v_{1},v_{2},\ldots , v_{k}$
are exactly
![]() $1,$
we see that it is enough to consider the intersection
$1,$
we see that it is enough to consider the intersection
where
![]() $C_{i}=A_{i}\cap [1,b_{i}].$
The idea is to use Theorem 3.3 and Lemma 5.3 inductively. We find large (in diameter) and thick (in normalized thickness) Cantor sets contained in
$C_{i}=A_{i}\cap [1,b_{i}].$
The idea is to use Theorem 3.3 and Lemma 5.3 inductively. We find large (in diameter) and thick (in normalized thickness) Cantor sets contained in
![]() $C_{1}\cap C_{2}, C_{1}\cap C_{2}\cap C_{3},\ldots , C_{1}\cap \cdots \cap C_{k}.$
After that, we show that this procedure still goes through if one changes
$C_{1}\cap C_{2}, C_{1}\cap C_{2}\cap C_{3},\ldots , C_{1}\cap \cdots \cap C_{k}.$
After that, we show that this procedure still goes through if one changes
![]() $C_{1},\ldots ,C_{k}$
by applying affine maps. This helps us to restore the information when
$C_{1},\ldots ,C_{k}$
by applying affine maps. This helps us to restore the information when
![]() $v_{1},\ldots ,v_{k}$
are almost but not exactly one.
$v_{1},\ldots ,v_{k}$
are almost but not exactly one.
Now,
![]() $C_{i}$
is a self-similar set with contraction ratio
$C_{i}$
is a self-similar set with contraction ratio
![]() $1/b_{i}.$
Indeed,
$1/b_{i}.$
Indeed,
are all scaled copies of
![]() $C_{i}.$
The largest bounded gaps of
$C_{i}.$
The largest bounded gaps of
![]() $C_{i}$
are of length
$C_{i}$
are of length
![]() $1/(b_{i}-1)$
and
$1/(b_{i}-1)$
and
![]() $S(C_{i})=(b_{i}-2)/(b_{i}-1).$
$S(C_{i})=(b_{i}-2)/(b_{i}-1).$
We now start to show the base step for the inductive argument. It is simple to check that
![]() $C_{1}\cap [1,2],C_{2}\cap [1,2]$
satisfy the gap condition of Theorem 3.3. Thus for each
$C_{1}\cap [1,2],C_{2}\cap [1,2]$
satisfy the gap condition of Theorem 3.3. Thus for each
![]() $\delta>0,$
we can find a compact subset
$\delta>0,$
we can find a compact subset
![]() $C_{1,2}\subset C_{1}\cap C_{2}\cap [1,2]$
with
$C_{1,2}\subset C_{1}\cap C_{2}\cap [1,2]$
with
![]() $S(C_{1,2})>1-\delta $
as long as
$S(C_{1,2})>1-\delta $
as long as
![]() $b_{1},b_{2}$
are sufficiently large.
$b_{1},b_{2}$
are sufficiently large.
We now show that the diameter of
![]() $C_{1,2}$
can be arbitrarily close to one at the cost of making
$C_{1,2}$
can be arbitrarily close to one at the cost of making
![]() $b_{1},b_{2}$
sufficiently large. By Lemma 5.3, we see that as long as
$b_{1},b_{2}$
sufficiently large. By Lemma 5.3, we see that as long as
![]() $b_{1},b_{2}$
are large enough, there is a compact set
$b_{1},b_{2}$
are large enough, there is a compact set
![]() $C_{1,2}\subset C_{1}\cap C_{2}\cap [1,2]$
with thickness and diameter both at least
$C_{1,2}\subset C_{1}\cap C_{2}\cap [1,2]$
with thickness and diameter both at least
![]() $1-\delta .$
$1-\delta .$
We can apply the same argument inside the intervals
![]() $[2,3],[3,4],\ldots ,[b_{1}-1,b_{1}].$
We now replace
$[2,3],[3,4],\ldots ,[b_{1}-1,b_{1}].$
We now replace
![]() $C_{1,2}$
with the union of all such compact sets (in
$C_{1,2}$
with the union of all such compact sets (in
![]() $[1,2], [2,3],\ldots $
).
$[1,2], [2,3],\ldots $
).
To summarize, for each
![]() $\delta>0,$
as long as
$\delta>0,$
as long as
![]() $b_{1},b_{2}$
are large enough, we can find a compact set
$b_{1},b_{2}$
are large enough, we can find a compact set
![]() $C_{1,2}\subset C_{1}\cap C_{2}$
so that for each
$C_{1,2}\subset C_{1}\cap C_{2}$
so that for each
![]() $l\in \{1,\ldots ,b_{1}-1\}$
,
$l\in \{1,\ldots ,b_{1}-1\}$
,
![]() $S(C_{1,2}\cap [l,l+1]), \lvert \mathrm{Conv(C_{1,2}\cap [l,l+1])}\rvert $
are at least
$S(C_{1,2}\cap [l,l+1]), \lvert \mathrm{Conv(C_{1,2}\cap [l,l+1])}\rvert $
are at least
![]() $1-\delta .$
$1-\delta .$
From the second part of Lemma 5.3, we conclude that for each
![]() $\delta>0,$
as long as
$\delta>0,$
as long as
![]() $b_{1},b_{2}$
are large enough, there is a number
$b_{1},b_{2}$
are large enough, there is a number
![]() $c>0$
such that for all affine maps
$c>0$
such that for all affine maps
![]() $T_{1},T_{2}$
with scaling ratios c-close to one and translations c-close to zero, there is a compact set
$T_{1},T_{2}$
with scaling ratios c-close to one and translations c-close to zero, there is a compact set
![]() $C_{1,2}\subset T_{1}(C_{1})\cap T_{2}(C_{2})$
such that for each
$C_{1,2}\subset T_{1}(C_{1})\cap T_{2}(C_{2})$
such that for each
![]() $l\in \{1,\ldots ,b_{1}-1\}$
,
$l\in \{1,\ldots ,b_{1}-1\}$
,
![]() $S(C_{1,2}\cap [l,l+1])$
and
$S(C_{1,2}\cap [l,l+1])$
and
![]() $\lvert \mathrm{Conv(C_{1,2}\cap [l,l+1])}\rvert $
are both larger than
$\lvert \mathrm{Conv(C_{1,2}\cap [l,l+1])}\rvert $
are both larger than
![]() $1-\delta $
. Moreover, it is possible to see that
$1-\delta $
. Moreover, it is possible to see that
![]() $\mathrm{Conv(C_{1,2}\cap [l,l+1])}\neq [l,l+1].$
This is because if c is small enough, then
$\mathrm{Conv(C_{1,2}\cap [l,l+1])}\neq [l,l+1].$
This is because if c is small enough, then
![]() $\mathrm{Conv(T_{1}(C_{1})\cap [l,l+1])}\neq [l,l+1], \mathrm{Conv(T_{2}(C_{2})\cap [l,l+1])}\neq [l,l+1]$
. This finishes the base step.
$\mathrm{Conv(T_{1}(C_{1})\cap [l,l+1])}\neq [l,l+1], \mathrm{Conv(T_{2}(C_{2})\cap [l,l+1])}\neq [l,l+1]$
. This finishes the base step.
We now perform the induction. Let
![]() $j\in \{2,3\ldots ,k-1\}$
. Suppose that for each
$j\in \{2,3\ldots ,k-1\}$
. Suppose that for each
![]() $\delta>0,$
as long as
$\delta>0,$
as long as
![]() $b_{1},\ldots ,b_{j}$
are large enough, there is a number
$b_{1},\ldots ,b_{j}$
are large enough, there is a number
![]() $c>0$
such that as long as
$c>0$
such that as long as
![]() $r_{1},\ldots ,r_{j}\in (1-c,1+c)$
,
$r_{1},\ldots ,r_{j}\in (1-c,1+c)$
,
![]() $t_{1},\ldots ,t_{j}\in (-c,c)$
, we can find a compact set
$t_{1},\ldots ,t_{j}\in (-c,c)$
, we can find a compact set
 $$ \begin{align*} C_{1,2,\ldots,j}\subset \bigcap_{i=1}^{j} T_{i}(C_{i}) \end{align*} $$
$$ \begin{align*} C_{1,2,\ldots,j}\subset \bigcap_{i=1}^{j} T_{i}(C_{i}) \end{align*} $$
such that for each
![]() $l\in \{1,\ldots ,b_{1}-1\}$
, we have that
$l\in \{1,\ldots ,b_{1}-1\}$
, we have that
![]() $\mathrm{Conv(C_{1,2\ldots ,j}\cap [l,l+1])}\neq [l,l+1]$
, and that
$\mathrm{Conv(C_{1,2\ldots ,j}\cap [l,l+1])}\neq [l,l+1]$
, and that
are greater than
![]() $1-\delta $
, where
$1-\delta $
, where
![]() $T_{i},i\in \{1,\ldots ,j\}$
are linear maps
$T_{i},i\in \{1,\ldots ,j\}$
are linear maps
![]() $x\to r_{i}x+t_{1}.$
We call this statement to be
$x\to r_{i}x+t_{1}.$
We call this statement to be
![]() $ST(j).$
Under
$ST(j).$
Under
![]() $ST(j),$
inside each interval
$ST(j),$
inside each interval
![]() $[l,l+1],l\in \{1,\ldots ,b_{1}-1\}$
, it is possible to use Lemma 5.3 for
$[l,l+1],l\in \{1,\ldots ,b_{1}-1\}$
, it is possible to use Lemma 5.3 for
![]() $C_{1,2\ldots ,j}$
and
$C_{1,2\ldots ,j}$
and
![]() $C_{j+1}$
. From here, we see that
$C_{j+1}$
. From here, we see that
![]() $ST(j+1)$
holds.
$ST(j+1)$
holds.
Finally, by induction, we see that
![]() $ST(k)$
holds. Thus there is a small number
$ST(k)$
holds. Thus there is a small number
![]() $c>0$
such that as long as
$c>0$
such that as long as
![]() $r_{1},r_{2},\ldots ,r_{k}\in (1-c,1+c)$
and
$r_{1},r_{2},\ldots ,r_{k}\in (1-c,1+c)$
and
![]() $t_{1},t_{2},\ldots ,t_{k}\in (-c,c)$
, we can find a compact set
$t_{1},t_{2},\ldots ,t_{k}\in (-c,c)$
, we can find a compact set
 $$ \begin{align*} C_{1,2,\ldots,k}\subset \bigcap_{i=1}^{k} T_{i}(C_{i}) \end{align*} $$
$$ \begin{align*} C_{1,2,\ldots,k}\subset \bigcap_{i=1}^{k} T_{i}(C_{i}) \end{align*} $$
such that for each
![]() $l\in \{1,\ldots ,b_{1}-1\}, C_{1,2,\ldots ,k}\cap [l,l+1]$
has thickness at least
$l\in \{1,\ldots ,b_{1}-1\}, C_{1,2,\ldots ,k}\cap [l,l+1]$
has thickness at least
![]() $1-\delta $
and diameter at least
$1-\delta $
and diameter at least
![]() $1-\delta ,$
where
$1-\delta ,$
where
![]() $T_{i}:x\to r_{i}x+t_{i}$
. In particular, we see that
$T_{i}:x\to r_{i}x+t_{i}$
. In particular, we see that
 $\bigcap _{i=1}^{k} T_{i}(C_{i})\neq \emptyset .$
Now we can choose
$\bigcap _{i=1}^{k} T_{i}(C_{i})\neq \emptyset .$
Now we can choose
![]() $\delta ^{\prime }$
in equation (8) to be small enough according to c. We can then rescale this situation by
$\delta ^{\prime }$
in equation (8) to be small enough according to c. We can then rescale this situation by
![]() $b^{n}_{1}$
and conclude that
$b^{n}_{1}$
and conclude that
We proved that for sufficiently large
![]() $b_{1},\ldots ,b_{k},$
there are infinitely many
$b_{1},\ldots ,b_{k},$
there are infinitely many
![]() $n\geq 0$
such that
$n\geq 0$
such that
This implies that
![]() $A=A_{1}\cap A_{2}\cap \cdots \cap A_{k}$
is unbounded, and the proof of the theorem is finished.
$A=A_{1}\cap A_{2}\cap \cdots \cap A_{k}$
is unbounded, and the proof of the theorem is finished.
Acknowledgements
H.Y. was financially supported by the University of Cambridge and the Corpus Christi College, Cambridge. H.Y. has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 803711). H.Y. especially thanks an anonymous referee for many instructive comments, which helped to improve the manuscript significantly.