Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-30T05:04:19.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansion properties of double standard maps

Part of: Low-dimensional dynamical systems Smooth dynamical systems: general theory

Published online by Cambridge University Press:  05 July 2022

MICHAEL BENEDICKS Open the ORCID record for MICHAEL BENEDICKS [Opens in a new window] ,
MICHAL MISIUREWICZ Open the ORCID record for MICHAL MISIUREWICZ [Opens in a new window]  and
ANA RODRIGUES
MICHAEL BENEDICKS*
Affiliation:
Matematiska Institutionen, KTH, Lindstedtsvägen 25, S-100 44 Stockholm, Sweden
MICHAL MISIUREWICZ
Affiliation:
Department of Mathematical Sciences, IUPUI, 402 N. Blackford Street, Indianapolis, IN 46202, USA (e-mail: [email protected])
ANA RODRIGUES
Affiliation:
Department of Mathematics, Exeter University, Exeter EX4 4QF, UK (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For the family of double standard maps 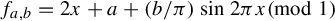$f_{a,b}=2x+a+({b}/{\pi }) \sin 2\pi x \pmod {1}$ we investigate the structure of the space of parameters a when 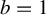$b=1$ and when $b\in [0,1)$. In the first case the maps have a critical point, but for a set of parameters 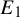$E_1$ of positive Lebesgue measure there is an invariant absolutely continuous measure for 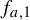$f_{a,1}$. In the second case there is an open non-empty set 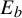$E_b$ of parameters for which the map 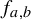$f_{a,b}$ is expanding. 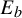We show that as $b\nearrow 1$, the set $E_b$ accumulates on many points of 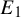$E_1$ in a regular way from the measure point of view.

Keywords

double standards mapsabsolutely continuous invariant measureexpansion

MSC classification

Primary: 37E10: Maps of the circle
Secondary: 37C40: Smooth ergodic theory, invariant measures
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 8 , August 2023 , pp. 2549 - 2588
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, V. I.. Small denominators. I. Mappings of the circumference onto itself. Amer. Math. Soc. Transl. 46 (1965), 213–284.Google Scholar
Benedicks, M. and Carleson, L.. On iterations of $1-a{x}^2$ on $\left(-1,1\right)$ . Ann. of Math. (2) 122(1) (1985), 1–25.CrossRefGoogle Scholar
Benedicks, M. and Carleson, L.. The dynamics of the Hénon map. Ann. of Math. (2) 133(1) (1991), 73–169.10.2307/2944326CrossRefGoogle Scholar
Benedicks, M. and Rodrigues, A.. Kneading sequences for double standard maps. Fund. Math. 206 (2009), 61–75.CrossRefGoogle Scholar
Bruin, H., Luzzatto, S. and van Strien, S.. Decay of correlations in one-dimensional dynamics. Ann. Sci. Éc. Norm. Supér. (4) 36(4) (2003), 621–646.CrossRefGoogle Scholar
Bruin, H., Rivera-Letelier, J., van Strien, S. and Shen, W.. Large derivatives, backward contraction and invariant densities for interval maps. Invent. Math. 172(3) (2008), 509–533.CrossRefGoogle Scholar
Collet, P. and Eckmann, J.-P.. On the abundance of aperiodic behaviour for maps on the interval. Comm. Math. Phys. 73 (1980) 115–160.CrossRefGoogle Scholar
de Melo, W. and van Strien, S.. One-Dimensional Dynamics (Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 25). Springer-Verlag, Berlin, 1993.CrossRefGoogle Scholar
Dezotti, A.. Connectedness of the Arnold tongues for double standard maps. Proc. Amer. Math. Soc. 138 (2010), 3569–3583.CrossRefGoogle Scholar
Fagella, N. and Garijo, A.. The parameter planes of $\lambda {z}^m\exp (z)$ for $m\ge 2$ . Comm. Math. Phys. 273 (2007), 755–783.10.1007/s00220-007-0265-8CrossRefGoogle Scholar
Jakobson, M.. Absolutely continuous invariant measures for one-parameter families of one-dimensional maps. Comm. Math. Phys. 81 (1981), 39–88.CrossRefGoogle Scholar
Krzyżewski, K. and Szlenk, W.. On invariant measures for expanding differentiable mappings. Studia Math. 33 (1969), 83–92.CrossRefGoogle Scholar
Lasota, A. and Yorke, J. A.. On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc. 186 (1973), 481–488.10.1090/S0002-9947-1973-0335758-1CrossRefGoogle Scholar
Levin, G. and Świątek, G.. Universality of critical circle covers. Comm. Math. Phys. 228 (2002), 371–399.CrossRefGoogle Scholar
Levin, G. and van Strien, S.. Bounds for maps of an interval with one critical point of inflection type. II. Invent. Math. 141(2) (2000), 399–465.CrossRefGoogle Scholar
Mañé, R.. Hyperbolicity, sinks and measure in one-dimensional dynamics. Comm. Math. Phys. 100 (1985), 495–524.CrossRefGoogle Scholar
Misiurewicz, M.. Absolutely continuous measures for certain maps of an interval. Publ. Math. Inst. Hautes Études Sci. 53 (1981), 17–51.10.1007/BF02698686CrossRefGoogle Scholar
Misiurewicz, M.,Iooss, G.,Helleman, R. H. G. andStora, R. (eds.)Maps of an interval. Chaotic Behaviour of Deterministic Systems. North-Holland, Amsterdam, 1983, pp. 565–590.Google Scholar
Misiurewicz, M. and Rodrigues, A.. Double standard maps. Comm. Math. Phys. 273 (2007), 37–65.CrossRefGoogle Scholar
Misiurewicz, M. and Rodrigues, A.. On the tip of the tongue. J. Fixed Point Theory Appl. 3 (2008), 131–141.CrossRefGoogle Scholar
Misiurewicz, M. and Rodrigues, A.. Non-generic cusps. Trans. Amer. Math. Soc. 363 (2011), 3553–3572.CrossRefGoogle Scholar
Nowicki, T. and van Strien, S.. Absolutely continuous invariant measures for ${C}^2$ unimodal maps satisfying the Collet–Eckmann conditions. Invent. Math. 93 (1988), 619–635.CrossRefGoogle Scholar
Shub, M. and Sullivan, D.. Expanding endomorphisms of the circle revisited. Ergod. Th. & Dynam. Sys. 5 (1985), 285–289.CrossRefGoogle Scholar
Thieullen, P., Tresser, C. and Young, L.-S.. Positive Lyapunov exponent for generic one-parameter families of unimodal maps. J. Anal. Math. 64 (1994), 121–172.CrossRefGoogle Scholar
van Strien, S.. Hyperbolicity and invariant measures for general ${C}^2$ interval maps satisfying the Misiurewicz condition. Comm. Math. Phys. 128 (1990), 437–496.CrossRefGoogle Scholar