Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T21:09:52.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Divergent trajectories in arithmetic homogeneous spaces of rational rank two

Part of: Diophantine approximation, transcendental number theory Lie groups

Published online by Cambridge University Press:  05 November 2020

NATTALIE TAMAM
NATTALIE TAMAM*
Affiliation:
Department of Mathematics, Tel Aviv University, Tel Aviv, Israel (e-mail: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a semisimple real algebraic group defined over 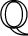${\mathbb {Q}}$ , $\Gamma $ be an arithmetic subgroup of G, and T be a maximal 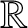${\mathbb {R}}$ -split torus. A trajectory in 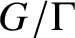$G/\Gamma $ is divergent if eventually it leaves every compact subset. In some cases there is a finite collection of explicit algebraic data which accounts for the divergence. If this is the case, the divergent trajectory is called obvious. Given a closed cone in T, we study the existence of non-obvious divergent trajectories under its action in 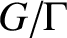$G\kern-1pt{/}\kern-1pt\Gamma $ . We get a sufficient condition for the existence of a non-obvious divergence trajectory in the general case, and a full classification under the assumption that 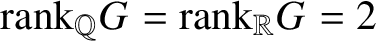$\mathrm {rank}_{{\mathbb {Q}}}G=\mathrm {rank}_{{\mathbb {R}}}G=2$ .

Keywords

group actionshomogeneous dynamicsarithmetic groupsLie groups representation

MSC classification

Primary: 22E40: Discrete subgroups of Lie groups
Secondary: 11J13: Simultaneous homogeneous approximation, linear forms
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 10 , October 2021 , pp. 3116 - 3141
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

REFERENCES

Borel, A.. Linear Algebraic Groups (Graduate texts in Mathematics, 126), 2nd enlarged edn. Springer, New York 1991.CrossRefGoogle Scholar
Bourbaki, N.. Lie Groups and Lie Algebras. Springer, Berlin, 2002, Chs. 4–6.CrossRefGoogle Scholar
Bourbaki, N.. Lie Groups and Lie Algebras . Springer, Berlin, 2005, Chs. 7–9.Google Scholar
Borel, A. and Tits, J.. Groupes réductifs. Publ. Math. Inst. Hautes Études Sci. 27 (1965), 55–150.CrossRefGoogle Scholar
Dani, G.. Divergent trajectories of flows on homogeneous spaces and diophantine approximation. J. Reine Angew. Math. 359 (1985), 55–89.Google Scholar
Goluzin, G. M.. Geometric Theory of Functions of a Complex Variable. American Mathematical Society, Providence, RI, 1969.CrossRefGoogle Scholar
Hall, B. C.. Lie Groups, Lie Algebras, and Representations: An Elementary Introduction ( Graduate Texts in Mathematics , 222), 2nd edn. Springer, New York, 2015.CrossRefGoogle Scholar
Helgason, S.. Differential Geometry, Lie Groups and Symmetric Spaces. Academic Press, New York, 1978.Google Scholar
Hoffman, K. and Kunze, R.. Linear Algebra, 2nd edn. Prentice-Hall, Englewood Cliffs, NJ, 1971.Google Scholar
Humphreys, J. E.. Linear Algebraic Groups ( Graduate Texts in Mathematics , 21). Springer, New York, 1975.CrossRefGoogle Scholar
Karasev, R. N.. Covering dimension using toric varieties. Topology Appl. 177 (2014), 59–65.CrossRefGoogle Scholar
Knapp, A. W.. Lie Groups Beyond an Introduction, 2nd edn. Birkhäuser, Boston, MA, 1996.CrossRefGoogle Scholar
Kleinbock, D., Shah, N. A. and Starkov, A. N.. Dynamics of subgroup actions on homogeneous spaces of Lie groups and applications to number theory. Handbook of Dynamical Systems. Vol. 1A. North-Holland, Amsterdam, 2002, pp. 813–930.Google Scholar
Kleinbock, D. and Weiss, B.. Modified Schmidt games and a conjecture of Margulis. J. Mod. Dyn. 7 (2013), 429–460.CrossRefGoogle Scholar
Spivak, M.. A Comprehensive Introduction to Differential Geometry. Vol. I, 2nd edn. Publish or Perish, Wilmington, DE, 1979.Google Scholar
Tomanov, G. and Weiss, B.. Closed orbits for actions of maximal tori on homogeneous spaces. Duke Math. J. 119(2) (2003), 367–392.10.1215/S0012-7094-03-11926-2CrossRefGoogle Scholar
Weiss, B.. Divergent trajectories on noncompact parameter spaces. Geom. Funct. Anal. 14(1) (2004), 94–149.CrossRefGoogle Scholar
Weiss, B.. Divergent trajectories and $\mathbb{Q}$ -rank . Israel J. Math. 152 (2006), 221–227.CrossRefGoogle Scholar
Yokonuma, T.. Tensor Spaces and Exterior Algebra. American Mathematical Society, Providence, RI, 1992.CrossRefGoogle Scholar