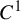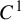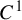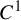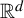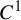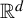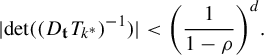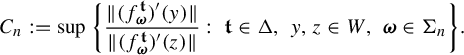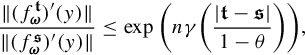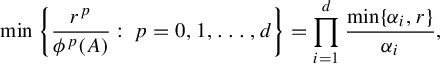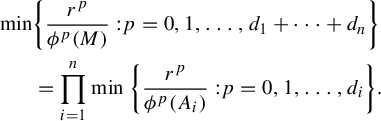1 Introduction
The present paper is a continuation of our work in [Reference Feng and Simon24] for studying the dimension theory of
![]() $C^1$
iterated function systems (IFSs) and repellers.
$C^1$
iterated function systems (IFSs) and repellers.
One of the fundamental problems in fractal geometry and dynamical systems is to compute various fractal dimensions of attractors of IFSs and associated invariant measures. The corresponding problem has been well understood when the underlying IFSs consist of similitudes or conformal maps satisfying certain separation conditions (see e.g. [Reference Bowen7, Reference Gatzouras and Peres25, Reference Hochman26, Reference Hutchinson30, Reference Patzschke39, Reference Przytycki and Urbański41, Reference Ruelle44]). The problem becomes substantially more difficult when the underlying IFSs are non-conformal. In the last three decades, much significant progress has been achieved for affine IFSs, see e.g. [Reference Bárány, Hochman and Rapaport2, Reference Bedford5, Reference Das and Simmons11, Reference Falconer13, Reference Falconer and Kempton19, Reference Feng and Shmerkin23, Reference Hochman and Rapaport27, Reference Jordan, Pollicott and Simon32, Reference Käenmäki34, Reference McMullen37], the references in the survey papers [Reference Chen and Pesin10, Reference Falconer17] and an upcoming book [Reference Bárány, Simon and Solomyak3].
In contrast to the extensive studies on affine IFSs, there have been relatively few results on those IFSs which are neither conformal nor affine. In 1994, Falconer [Reference Falconer15] introduced a quantity (known as the singularity dimension) in terms of sub-additive topological pressure, and showed that it is an upper bound for the upper box-counting dimension of repellers of
![]() $C^2$
expanding maps satisfying a ‘bunching’ condition. Later, in 1997, Zhang [Reference Zhang50] proved that this upper bound holds for the Hausdorff dimension of repellers of arbitrary
$C^2$
expanding maps satisfying a ‘bunching’ condition. Later, in 1997, Zhang [Reference Zhang50] proved that this upper bound holds for the Hausdorff dimension of repellers of arbitrary
![]() $C^1$
expanding maps. We remark that the results of Falconer and Zhang extend directly to the IFS setting. Recently, Cao, Pesin and Zhao [Reference Cao, Pesin and Zhao9] also gave an upper bound for the upper box-counting dimension of repellers of
$C^1$
expanding maps. We remark that the results of Falconer and Zhang extend directly to the IFS setting. Recently, Cao, Pesin and Zhao [Reference Cao, Pesin and Zhao9] also gave an upper bound for the upper box-counting dimension of repellers of
![]() $C^{1+\alpha }$
expanding maps satisfying a certain dominated splitting property. However that upper bound depends on the splitting involved and is usually strictly larger than the singularity dimension. In [Reference Feng and Simon24], the authors proved that the singularity dimension is an upper bound of the upper box-counting dimension of the attractor of every
$C^{1+\alpha }$
expanding maps satisfying a certain dominated splitting property. However that upper bound depends on the splitting involved and is usually strictly larger than the singularity dimension. In [Reference Feng and Simon24], the authors proved that the singularity dimension is an upper bound of the upper box-counting dimension of the attractor of every
![]() $C^1$
IFS or the repeller of every
$C^1$
IFS or the repeller of every
![]() $C^1$
expanding map, which improved the aforementioned results in [Reference Cao, Pesin and Zhao9, Reference Falconer15, Reference Zhang50]. The authors also established a measure analogue of this result, that is, the upper packing dimension of every ergodic invariant measure associated with a
$C^1$
expanding map, which improved the aforementioned results in [Reference Cao, Pesin and Zhao9, Reference Falconer15, Reference Zhang50]. The authors also established a measure analogue of this result, that is, the upper packing dimension of every ergodic invariant measure associated with a
![]() $C^1$
IFS or repeller is bounded above by its Lyapunov dimension, which improved an earlier result of Jordan and Pollicott [Reference Jordan and Pollicott31] for the upper Hausdorff dimension of measures. The reader is referred to §2.2 for the definitions of singularity dimension and Lyapunov dimension.
$C^1$
IFS or repeller is bounded above by its Lyapunov dimension, which improved an earlier result of Jordan and Pollicott [Reference Jordan and Pollicott31] for the upper Hausdorff dimension of measures. The reader is referred to §2.2 for the definitions of singularity dimension and Lyapunov dimension.
In [Reference Hu29], Hu computed the box-counting dimension of repellers of
![]() $C^2$
maps on
$C^2$
maps on
![]() ${\Bbb R}^2$
which have an invariant strong unstable foliation along which they expand more strongly than in the complementary directions. Very recently, Falconer, Fraser and Lee [Reference Falconer, Fraser and Lee18] computed the
${\Bbb R}^2$
which have an invariant strong unstable foliation along which they expand more strongly than in the complementary directions. Very recently, Falconer, Fraser and Lee [Reference Falconer, Fraser and Lee18] computed the
![]() $L^q$
-spectra of Bernoulli measures associated with a class of planar IFSs consisting of
$L^q$
-spectra of Bernoulli measures associated with a class of planar IFSs consisting of
![]() $C^{1+\alpha }$
maps for which the Jacobian is a lower triangular matrix subject to a domination condition and satisfying the rectangular open set condition. As a corollary, they obtained a formula for the box-counting dimension of the attractors of such planar IFSs. In another recent paper [Reference Jurga and Lee33], Jurga and Lee proved that, under slightly stronger assumptions, these Bernoulli measures (and more generally, quasiBernoulli measures) on the attractors are exact dimensional with dimension given by a Ledrappier–Young-type formula. In earlier related works, Bedford and Urbański [Reference Bedford and Urbański6] calculated the box-counting and Hausdorff dimensions of the attractors of a very special class of planar nonlinear triangular
$C^{1+\alpha }$
maps for which the Jacobian is a lower triangular matrix subject to a domination condition and satisfying the rectangular open set condition. As a corollary, they obtained a formula for the box-counting dimension of the attractors of such planar IFSs. In another recent paper [Reference Jurga and Lee33], Jurga and Lee proved that, under slightly stronger assumptions, these Bernoulli measures (and more generally, quasiBernoulli measures) on the attractors are exact dimensional with dimension given by a Ledrappier–Young-type formula. In earlier related works, Bedford and Urbański [Reference Bedford and Urbański6] calculated the box-counting and Hausdorff dimensions of the attractors of a very special class of planar nonlinear triangular
![]() $C^{1+\alpha }$
IFSs (of which the attractors are curves), Manning and Simon [Reference Manning and Simon36] and Bárány [Reference Bárány1] studied the sub-additive pressure associated with nonlinear
$C^{1+\alpha }$
IFSs (of which the attractors are curves), Manning and Simon [Reference Manning and Simon36] and Bárány [Reference Bárány1] studied the sub-additive pressure associated with nonlinear
![]() $C^{1+\alpha }$
IFSs whose maps have triangular Jacobians.
$C^{1+\alpha }$
IFSs whose maps have triangular Jacobians.
In this paper, we introduce a generalized transversality condition (GTC) for parameterized families of
![]() $C^1$
IFSs on
$C^1$
IFSs on
![]() ${\Bbb R}^d$
, and show that if the GTC is satisfied, then for almost every (a.e.) (in an appropriate sense) parameter, the Hausdorff and box-counting dimensions of the IFS attractor are indeed given by the singularity dimension, and the dimension of ergodic invariant measures on the attractor is given by its Lyapunov dimension. Moreover, we will verify the GTC for several classes of translational families of
${\Bbb R}^d$
, and show that if the GTC is satisfied, then for almost every (a.e.) (in an appropriate sense) parameter, the Hausdorff and box-counting dimensions of the IFS attractor are indeed given by the singularity dimension, and the dimension of ergodic invariant measures on the attractor is given by its Lyapunov dimension. Moreover, we will verify the GTC for several classes of translational families of
![]() $C^1$
IFSs.
$C^1$
IFSs.
Before formulating our results precisely, we first recall some basic notation and definitions. By a
![]() $C^1$
IFS on a compact set
$C^1$
IFS on a compact set
![]() $Z\subset {\Bbb R}^d$
, we mean a finite collection
$Z\subset {\Bbb R}^d$
, we mean a finite collection
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
of self-maps on Z, such that there exists an open set
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
of self-maps on Z, such that there exists an open set
![]() $U\supset Z$
so that each
$U\supset Z$
so that each
![]() $f_i$
extends to a
$f_i$
extends to a
![]() $C^1$
-diffeomorphism
$C^1$
-diffeomorphism
![]() $f_i: U\to f_i(U)\subset U$
with
$f_i: U\to f_i(U)\subset U$
with
where
![]() $D_xf$
stands for the differential of f at x and
$D_xf$
stands for the differential of f at x and
![]() $\|\cdot \|$
is the standard matrix norm (that is,
$\|\cdot \|$
is the standard matrix norm (that is,
![]() $\|A\|$
is the largest singular value of A).
$\|A\|$
is the largest singular value of A).
Let K be the attractor of the IFS
![]() $\mathcal F$
, that is, K is the unique non-empty compact subset of Z such that
$\mathcal F$
, that is, K is the unique non-empty compact subset of Z such that
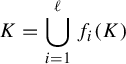 $$ \begin{align} K=\bigcup_{i=1}^{\ell} f_i(K) \end{align} $$
$$ \begin{align} K=\bigcup_{i=1}^{\ell} f_i(K) \end{align} $$
(cf. [Reference Hutchinson30]).
Let
![]() $(\Sigma ,\sigma )$
be the one-sided full shift over the alphabet
$(\Sigma ,\sigma )$
be the one-sided full shift over the alphabet
![]() $\{1,\ldots , \ell \}$
. Let
$\{1,\ldots , \ell \}$
. Let
![]() $\Pi : \Sigma \to K$
denote the corresponding coding map associated with the IFS
$\Pi : \Sigma \to K$
denote the corresponding coding map associated with the IFS
![]() $\mathcal F$
, that is,
$\mathcal F$
, that is,
It is well known that
![]() $\Pi $
is continuous and surjective [Reference Hutchinson30]. For a
$\Pi $
is continuous and surjective [Reference Hutchinson30]. For a
![]() $\sigma $
-invariant Borel probability measure
$\sigma $
-invariant Borel probability measure
![]() $\mu $
on
$\mu $
on
![]() $\Sigma $
, let
$\Sigma $
, let
![]() $\Pi _*\mu $
denote the push-forward of
$\Pi _*\mu $
denote the push-forward of
![]() $\mu $
by
$\mu $
by
![]() $\Pi $
, that is,
$\Pi $
, that is,
![]() $\Pi _*\mu (E)=\mu (\Pi ^{-1}(E))$
for each Borel subset E of
$\Pi _*\mu (E)=\mu (\Pi ^{-1}(E))$
for each Borel subset E of
![]() ${\Bbb R}^d$
.
${\Bbb R}^d$
.
For a Borel probability measure
![]() $\xi $
on
$\xi $
on
![]() ${\Bbb R}^d$
, we call
${\Bbb R}^d$
, we call
the lower and upper local dimensions of
![]() $\xi $
at x, where
$\xi $
at x, where
![]() $B(x,r)$
stands for the closed ball centered at x of radius r. Moreover, we call
$B(x,r)$
stands for the closed ball centered at x of radius r. Moreover, we call
the lower Hausdorff dimension and upper packing dimension of
![]() $\xi $
, respectively. If
$\xi $
, respectively. If
![]() $\underline {\dim }_H\xi =\overline {\dim }_P\xi $
, we say that
$\underline {\dim }_H\xi =\overline {\dim }_P\xi $
, we say that
![]() $\xi $
is exact dimensional and write
$\xi $
is exact dimensional and write
![]() $\dim \xi $
or
$\dim \xi $
or
![]() $\dim _H \xi $
for this common value.
$\dim _H \xi $
for this common value.
To introduce the notion of GTC, let
![]() $\ell \geq 2$
and let
$\ell \geq 2$
and let
![]() ${\mathcal F}^t=\{f_1^t,\ldots , f_{\ell }^t\}$
,
${\mathcal F}^t=\{f_1^t,\ldots , f_{\ell }^t\}$
,
![]() $t\in {\Omega }$
, be a parameterized family of
$t\in {\Omega }$
, be a parameterized family of
![]() $C^1$
IFSs defined on a common compact subset Z of
$C^1$
IFSs defined on a common compact subset Z of
![]() ${\Bbb R}^d$
, where
${\Bbb R}^d$
, where
![]() $({\Omega }, \rho )$
is a separable metric space, such that the following two conditions hold.
$({\Omega }, \rho )$
is a separable metric space, such that the following two conditions hold.
-
(C1) The maps
 $f_i^t$
have a common Lipschitz constant
$f_i^t$
have a common Lipschitz constant
 $\theta \in (0,1)$
, that is, (1.3)for all
$\theta \in (0,1)$
, that is, (1.3)for all $$ \begin{align} |f^t_i(x)-f^t_i(y)| \leq \theta |x-y| \end{align} $$
$$ \begin{align} |f^t_i(x)-f^t_i(y)| \leq \theta |x-y| \end{align} $$
 $1\leq i\leq \ell $
,
$1\leq i\leq \ell $
,
 $t\in {\Omega }$
and
$t\in {\Omega }$
and
 $x,y\in Z$
.
$x,y\in Z$
.
-
(C2) The mapping
 $t\mapsto f^t_i(x)$
is continuous over
$t\mapsto f^t_i(x)$
is continuous over
 ${\Omega }$
for every given
${\Omega }$
for every given
 $x\in Z$
and
$x\in Z$
and
 $1\leq i\leq \ell $
.
$1\leq i\leq \ell $
.
For each
![]() $t\in {\Omega }$
, let
$t\in {\Omega }$
, let
![]() $K^t$
denote the attractor of
$K^t$
denote the attractor of
![]() $\mathcal F^t$
, and let
$\mathcal F^t$
, and let
![]() $\Pi ^t:\; \Sigma \to {\Bbb R}^d$
denote the coding map associated with the IFS
$\Pi ^t:\; \Sigma \to {\Bbb R}^d$
denote the coding map associated with the IFS
![]() ${\mathcal F}^t$
. Due to the conditions (C1) and (C2), the mapping
${\mathcal F}^t$
. Due to the conditions (C1) and (C2), the mapping
![]() $(t,\mathbf {i})\mapsto \Pi ^t(\mathbf {i})$
is continuous over the product space
$(t,\mathbf {i})\mapsto \Pi ^t(\mathbf {i})$
is continuous over the product space
![]() ${\Omega }\times \Sigma $
.
${\Omega }\times \Sigma $
.
For
![]() $t\in {\Omega }$
,
$t\in {\Omega }$
,
![]() $r>0$
and
$r>0$
and
![]() ${\textbf {i}}\in \Sigma _*:=\bigcup _{n=0}^{\infty } \{1,\ldots , \ell \}^n$
, set
${\textbf {i}}\in \Sigma _*:=\bigcup _{n=0}^{\infty } \{1,\ldots , \ell \}^n$
, set
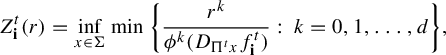 $$ \begin{align} Z_{\textbf{i}}^t(r)= \inf_{x\in \Sigma} \min\bigg \{ \frac{r^k}{ \phi^k (D_{\Pi^t x}f^t_{{\textbf{i}}} ) }:\; k=0, 1,\ldots, d\bigg\} , \end{align} $$
$$ \begin{align} Z_{\textbf{i}}^t(r)= \inf_{x\in \Sigma} \min\bigg \{ \frac{r^k}{ \phi^k (D_{\Pi^t x}f^t_{{\textbf{i}}} ) }:\; k=0, 1,\ldots, d\bigg\} , \end{align} $$
where
![]() $f^t_{{\textbf {i}}}:=f^t_{i_1}\circ \cdots \circ f^t_{i_n}$
for
$f^t_{{\textbf {i}}}:=f^t_{i_1}\circ \cdots \circ f^t_{i_n}$
for
![]() ${\textbf { i}}=i_1\ldots i_n$
,
${\textbf { i}}=i_1\ldots i_n$
,
![]() $f^t_{\varepsilon }$
denotes the identity map on
$f^t_{\varepsilon }$
denotes the identity map on
![]() ${\Bbb R}^d$
and
${\Bbb R}^d$
and
![]() $\phi ^s(\cdot )$
stands for the singular value function (see (2.5) for the definition).
$\phi ^s(\cdot )$
stands for the singular value function (see (2.5) for the definition).
Definition 1.1. Let
![]() $\eta $
be a locally finite Borel measure on
$\eta $
be a locally finite Borel measure on
![]() ${\Omega }$
. We say that the family
${\Omega }$
. We say that the family
![]() ${\mathcal F}^t$
,
${\mathcal F}^t$
,
![]() $t\in {\Omega }$
, satisfies a GTC with respect to
$t\in {\Omega }$
, satisfies a GTC with respect to
![]() $\eta $
if there exist
$\eta $
if there exist
![]() $\delta _0>0$
and a function
$\delta _0>0$
and a function
![]() $\psi : (0,\delta _0)\to [0,\infty )$
with
$\psi : (0,\delta _0)\to [0,\infty )$
with
![]() $\lim _{\delta \to 0}\psi (\delta )=0$
such that the following statement holds: for every
$\lim _{\delta \to 0}\psi (\delta )=0$
such that the following statement holds: for every
![]() $t_0\in {\Omega }$
and every
$t_0\in {\Omega }$
and every
![]() $0<\delta <\delta _0$
, there exists a constant
$0<\delta <\delta _0$
, there exists a constant
![]() $C=C(t_0, \delta )>0$
such that for all distinct
$C=C(t_0, \delta )>0$
such that for all distinct
![]() ${\textbf {i}}, {\textbf {j}}\in \Sigma $
and
${\textbf {i}}, {\textbf {j}}\in \Sigma $
and
![]() $r>0$
,
$r>0$
,
where
![]() $B(t_0,\delta )$
denotes the closed ball in
$B(t_0,\delta )$
denotes the closed ball in
![]() ${\Omega }$
of radius
${\Omega }$
of radius
![]() $\delta $
centered at t,
$\delta $
centered at t,
![]() $\mathbf {i}\wedge \mathbf {j}$
denotes the common initial segment of
$\mathbf {i}\wedge \mathbf {j}$
denotes the common initial segment of
![]() $\mathbf {i}$
and
$\mathbf {i}$
and
![]() $\mathbf {j}$
, and
$\mathbf {j}$
, and
![]() $|\mathbf {i}\wedge \mathbf {j}|$
is the length of the word
$|\mathbf {i}\wedge \mathbf {j}|$
is the length of the word
![]() $\mathbf {i}\wedge \mathbf {j}$
.
$\mathbf {i}\wedge \mathbf {j}$
.
The introduction of the GTC is inspired by the work of Jordan, Pollicott and Simon [Reference Jordan, Pollicott and Simon32], who defined the self-affine transversality condition for certain translational families of affine IFSs. The new feature here is that the upper bound term on the right-hand side of (1.5) depends upon
![]() $t_0$
,
$t_0$
,
![]() $\delta $
and
$\delta $
and
![]() $|{\textbf {i}}\wedge {\textbf {j}}|$
, while in the setting of [Reference Jordan, Pollicott and Simon32], the corresponding upper bound term is independent of these parameters and is determined by the linear parts of one pre-given affine IFS.
$|{\textbf {i}}\wedge {\textbf {j}}|$
, while in the setting of [Reference Jordan, Pollicott and Simon32], the corresponding upper bound term is independent of these parameters and is determined by the linear parts of one pre-given affine IFS.
For
![]() $t\in {\Omega }$
and a
$t\in {\Omega }$
and a
![]() $\sigma $
-invariant measure
$\sigma $
-invariant measure
![]() $\mu $
on
$\mu $
on
![]() $\Sigma $
, we write
$\Sigma $
, we write
for the singularity dimension of
![]() $\mathcal F^t$
and the Lyapunov dimension of
$\mathcal F^t$
and the Lyapunov dimension of
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $\mathcal F^t$
, respectively; see Definitions 2.3–2.4. For
$\mathcal F^t$
, respectively; see Definitions 2.3–2.4. For
![]() $E\subset {\Bbb R}^d$
, let
$E\subset {\Bbb R}^d$
, let
![]() $\dim _HE$
denote the Hausdorff dimension of E, and let
$\dim _HE$
denote the Hausdorff dimension of E, and let
![]() $\overline {\dim }_BE, \;\underline {\dim }_BE$
denote the upper and lower box-counting dimensions of E, respectively (cf. [Reference Falconer16]). When
$\overline {\dim }_BE, \;\underline {\dim }_BE$
denote the upper and lower box-counting dimensions of E, respectively (cf. [Reference Falconer16]). When
![]() $\overline {\dim }_BE=\underline {\dim }_BE$
, the common value is said to be the box-counting dimension of E and is denoted by
$\overline {\dim }_BE=\underline {\dim }_BE$
, the common value is said to be the box-counting dimension of E and is denoted by
![]() $\dim _BE$
.
$\dim _BE$
.
The first result of the present paper is the following.
Theorem 1.2. Let
![]() ${\mathcal F}^t=\{f_1^t,\ldots , f_{\ell }^t\}$
,
${\mathcal F}^t=\{f_1^t,\ldots , f_{\ell }^t\}$
,
![]() $t\in {\Omega }$
, be a parameterized family of
$t\in {\Omega }$
, be a parameterized family of
![]() $C^1$
IFSs defined on a common compact subset Z of
$C^1$
IFSs defined on a common compact subset Z of
![]() ${\Bbb R}^d$
, such that the conditions (C1)–(C2) hold. Let
${\Bbb R}^d$
, such that the conditions (C1)–(C2) hold. Let
![]() $\eta $
be a locally finite Borel measure on
$\eta $
be a locally finite Borel measure on
![]() ${\Omega }$
. Assume that
${\Omega }$
. Assume that
![]() $({\mathcal F}^t)_{t\in {\Omega }}$
satisfies the GTC with respect to
$({\mathcal F}^t)_{t\in {\Omega }}$
satisfies the GTC with respect to
![]() $\eta $
. Then the following properties hold.
$\eta $
. Then the following properties hold.
-
(i) Let
 $\mu $
be a
$\mu $
be a
 $\sigma $
-invariant ergodic measure on
$\sigma $
-invariant ergodic measure on
 $\Sigma $
. For
$\Sigma $
. For
 $\eta $
-a.e.
$\eta $
-a.e.
 $t\in {\Omega }$
,
$t\in {\Omega }$
,
 $\Pi ^t_*\mu $
is exact dimensional and Moreover,
$\Pi ^t_*\mu $
is exact dimensional and Moreover, $$ \begin{align*}\dim_H \Pi^t_*\mu=\min\{d, d_{\mu}(t)\}. \end{align*} $$
$$ \begin{align*}\dim_H \Pi^t_*\mu=\min\{d, d_{\mu}(t)\}. \end{align*} $$
 $\Pi ^t_*\mu \ll {\mathcal L}_d$
for
$\Pi ^t_*\mu \ll {\mathcal L}_d$
for
 $\eta $
-a.e.
$\eta $
-a.e.
 $t\in \{t'\in {\Omega }: d_{\mu }(t')>d\}$
, where
$t\in \{t'\in {\Omega }: d_{\mu }(t')>d\}$
, where
 ${\mathcal L}_d$
denotes the Lebesgue measure on
${\mathcal L}_d$
denotes the Lebesgue measure on
 ${\Bbb R}^d$
.
${\Bbb R}^d$
.
-
(ii) For
 $\eta $
-a.e.
$\eta $
-a.e.
 $t\in {\Omega }$
, Moreover,
$t\in {\Omega }$
, Moreover, $$ \begin{align*}\dim_H K^t=\dim_BK^t=\min\{d, d(t)\}. \end{align*} $$
$$ \begin{align*}\dim_H K^t=\dim_BK^t=\min\{d, d(t)\}. \end{align*} $$
 ${\mathcal L}_d(K^t)>0$
for
${\mathcal L}_d(K^t)>0$
for
 $\eta $
-a.e.
$\eta $
-a.e.
 $t\in \{t'\in {\Omega }: \; d(t')>d\}$
.
$t\in \{t'\in {\Omega }: \; d(t')>d\}$
.
The above theorem is a nonlinear analogue of the results of Jordan, Pollicott and Simon [Reference Jordan, Pollicott and Simon32, Theorems 4.2 and 4.3] for affine IFSs. We emphasize that in the nonlinear case, the singularity and Lyapunov dimensions depend on the parameter t, while in the affine case, the corresponding quantities are constant. This is a key difference between the affine case and the nonlinear case. We remark that Theorem 1.2 also extends and generalizes the corresponding results of Simon, Solomyak and Urbański ([Reference Simon, Solomyak and Urbański45, Theorem 3.1], [Reference Simon, Solomyak and Urbański46, Theorem 2.3]) for
![]() $C^{1+\alpha }$
conformal IFSs on
$C^{1+\alpha }$
conformal IFSs on
![]() ${\Bbb R}$
.
${\Bbb R}$
.
Now a natural question arises of how to verify the GTC for a parameterized family of
![]() $C^1$
IFSs. In what follows, we investigate this question for certain translational families of
$C^1$
IFSs. In what follows, we investigate this question for certain translational families of
![]() $C^1$
IFSs.
$C^1$
IFSs.
First we introduce some definitions.
Definition 1.3. Let
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
![]() $C^1$
IFS on a compact set
$C^1$
IFS on a compact set
![]() $Z\subset {\Bbb R}^d$
such that
$Z\subset {\Bbb R}^d$
such that
![]() $f_i(Z)\subset \mathrm {int}(Z)$
for each i. Set
$f_i(Z)\subset \mathrm {int}(Z)$
for each i. Set
where
![]() $\boldsymbol {\mathfrak {t}}=(\mathbf {t}_1,\ldots , \mathbf {t}_{\ell })\in {\Bbb R}^{\ell d}$
with
$\boldsymbol {\mathfrak {t}}=(\mathbf {t}_1,\ldots , \mathbf {t}_{\ell })\in {\Bbb R}^{\ell d}$
with
![]() ${\textbf {t}}_i\in {\Bbb R}^d$
. By continuity, there is a small
${\textbf {t}}_i\in {\Bbb R}^d$
. By continuity, there is a small
![]() $r_0>0$
such that
$r_0>0$
such that
![]() $f_i^{\boldsymbol {\mathfrak {t}}}(Z)\subset \mathrm {int}(Z)$
for every
$f_i^{\boldsymbol {\mathfrak {t}}}(Z)\subset \mathrm {int}(Z)$
for every
![]() $\boldsymbol {\mathfrak {t}}$
with
$\boldsymbol {\mathfrak {t}}$
with
![]() $|\boldsymbol {\mathfrak {t}}|<r_0$
and every i, where
$|\boldsymbol {\mathfrak {t}}|<r_0$
and every i, where
![]() $|\cdot |$
is the Euclidean norm. Set
$|\cdot |$
is the Euclidean norm. Set
![]() $\mathcal F^{\boldsymbol {\mathfrak {t}}}=\{f_i^{\boldsymbol {\mathfrak {t}}}\}_{i=1}^{\ell }$
for each
$\mathcal F^{\boldsymbol {\mathfrak {t}}}=\{f_i^{\boldsymbol {\mathfrak {t}}}\}_{i=1}^{\ell }$
for each
![]() $\boldsymbol {\mathfrak {t}}$
with
$\boldsymbol {\mathfrak {t}}$
with
![]() $|\boldsymbol {\mathfrak {t}}|<r_0$
. We call
$|\boldsymbol {\mathfrak {t}}|<r_0$
. We call
![]() $(\mathcal F^{\boldsymbol {\mathfrak {t}}})_{\boldsymbol {\mathfrak {t}}\in \Delta }$
, where
$(\mathcal F^{\boldsymbol {\mathfrak {t}}})_{\boldsymbol {\mathfrak {t}}\in \Delta }$
, where
![]() $\Delta :=\{\boldsymbol {\mathfrak {s}}\in {\Bbb R}^{\ell d}:\; |\boldsymbol {\mathfrak {s}}|<r_0\}$
, a translational family of IFSs generated by
$\Delta :=\{\boldsymbol {\mathfrak {s}}\in {\Bbb R}^{\ell d}:\; |\boldsymbol {\mathfrak {s}}|<r_0\}$
, a translational family of IFSs generated by
![]() $\mathcal F$
.
$\mathcal F$
.
Definition 1.4. Let
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
![]() $C^1$
IFS on a compact set
$C^1$
IFS on a compact set
![]() $Z\subset {\Bbb R}^d$
. We say that
$Z\subset {\Bbb R}^d$
. We say that
![]() $\mathcal F$
is dominated lower triangular, if for each
$\mathcal F$
is dominated lower triangular, if for each
![]() $z\in Z$
and
$z\in Z$
and
![]() $i\in \{1,\ldots , \ell \}$
, the Jacobian
$i\in \{1,\ldots , \ell \}$
, the Jacobian
![]() $D_zf_i$
of
$D_zf_i$
of
![]() $f_i$
at z is a lower triangular matrix such that
$f_i$
at z is a lower triangular matrix such that
We remark that in the above definition, the condition for an IFS to be dominated lower triangular is slightly weaker than that required in [Reference Falconer, Fraser and Lee18, Reference Jurga and Lee33].
Definition 1.5. Let
![]() $\ell \in {\Bbb N}$
with
$\ell \in {\Bbb N}$
with
![]() $\ell \geq 2$
. Assume for
$\ell \geq 2$
. Assume for
![]() $j=1,\ldots , n$
,
$j=1,\ldots , n$
,
![]() $\mathcal F_j=\{f_{i,j}\}_{i=1}^{\ell }$
is an IFS on
$\mathcal F_j=\{f_{i,j}\}_{i=1}^{\ell }$
is an IFS on
![]() $Z_j\subset {\Bbb R}^{q_j}$
. Let
$Z_j\subset {\Bbb R}^{q_j}$
. Let
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
be an IFS on
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
be an IFS on
![]() $Z_1\times \cdots \times Z_n\subset {\Bbb R}^{q_1}\times \cdots \times {\Bbb R}^{q_n}$
given by
$Z_1\times \cdots \times Z_n\subset {\Bbb R}^{q_1}\times \cdots \times {\Bbb R}^{q_n}$
given by
We say that
![]() $\mathcal F$
is the direct product of
$\mathcal F$
is the direct product of
![]() $\mathcal F_1,\ldots , \mathcal F_n$
, and write
$\mathcal F_1,\ldots , \mathcal F_n$
, and write
![]() $\mathcal F=\mathcal F_1\times \cdots \times \mathcal F_n$
.
$\mathcal F=\mathcal F_1\times \cdots \times \mathcal F_n$
.
Now we are ready to state the second main result of the paper.
Theorem 1.6. Let
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
![]() $C^1$
IFS on a compact set
$C^1$
IFS on a compact set
![]() $Z\subset {\Bbb R}^d$
such that
$Z\subset {\Bbb R}^d$
such that
![]() $f_i(Z)\subset \mathrm {int} (Z)$
for each i. Suppose either one of the following three conditions holds.
$f_i(Z)\subset \mathrm {int} (Z)$
for each i. Suppose either one of the following three conditions holds.
-
(i)
 $\mathcal F$
is dominated lower triangular on Z satisfying (1.8)and Z is convex.
$\mathcal F$
is dominated lower triangular on Z satisfying (1.8)and Z is convex. $$ \begin{align} \max_{i\neq j}\Big(\sup_{y,z\in Z} \|D_yf_i\|+\|D_zf_j\|\Big)<1, \end{align} $$
$$ \begin{align} \max_{i\neq j}\Big(\sup_{y,z\in Z} \|D_yf_i\|+\|D_zf_j\|\Big)<1, \end{align} $$
-
(ii)
 $\mathcal F$
is a
$\mathcal F$
is a
 $C^1$
conformal IFS on Z satisfying (1.8), and Z is connected.
$C^1$
conformal IFS on Z satisfying (1.8), and Z is connected. -
(iii)
 $\mathcal F=\mathcal F_1\times \cdots \times \mathcal F_n$
, where for each
$\mathcal F=\mathcal F_1\times \cdots \times \mathcal F_n$
, where for each
 $k\in \{1,\ldots , n\}$
,
$k\in \{1,\ldots , n\}$
,
 $\mathcal F_k$
is a
$\mathcal F_k$
is a
 $C^1$
IFS on a compact
$C^1$
IFS on a compact
 $Z_k\subset {\Bbb R}^{d_k}$
satisfying either (i) or (ii), in which
$Z_k\subset {\Bbb R}^{d_k}$
satisfying either (i) or (ii), in which
 $\mathcal F$
and Z are replaced by
$\mathcal F$
and Z are replaced by
 $\mathcal F_k$
and
$\mathcal F_k$
and
 $Z_k$
, respectively.
$Z_k$
, respectively.
Then there is a small
![]() $r_0>0$
such that the translational family
$r_0>0$
such that the translational family
satisfies the GTC with respect to the Lebesgue measure
![]() $\mathcal L_{\ell d}$
on
$\mathcal L_{\ell d}$
on
![]() $\Delta $
. As a consequence, the conclusions of Theorem 1.2 hold for the family
$\Delta $
. As a consequence, the conclusions of Theorem 1.2 hold for the family
![]() $(\mathcal F^{\boldsymbol {\mathfrak {t}}})_{\boldsymbol {\mathfrak {t}}\in \Delta }$
.
$(\mathcal F^{\boldsymbol {\mathfrak {t}}})_{\boldsymbol {\mathfrak {t}}\in \Delta }$
.
The above theorem is a (partial) nonlinear extension of the corresponding results in [Reference Falconer13, Reference Jordan, Pollicott and Simon32, Reference Solomyak47] for affine IFSs. Recall that in the case when
![]() $\mathcal F=\{f_i(x)=A_ix+a_i\}_{i=1}^{\ell }$
is an affine IFS on
$\mathcal F=\{f_i(x)=A_ix+a_i\}_{i=1}^{\ell }$
is an affine IFS on
![]() ${\Bbb R}^d$
, under the assumption that
${\Bbb R}^d$
, under the assumption that
Falconer [Reference Falconer13] proved that the dimension of the attractor of
![]() $\mathcal F^{\boldsymbol {\mathfrak {t}}}=\{f_i+{\textbf {t}}_i\}_{i=1}^{\ell }$
is equal to its affinity dimension for
$\mathcal F^{\boldsymbol {\mathfrak {t}}}=\{f_i+{\textbf {t}}_i\}_{i=1}^{\ell }$
is equal to its affinity dimension for
![]() ${\mathcal L}_{\ell d}$
-a.e.
${\mathcal L}_{\ell d}$
-a.e.
![]() $\boldsymbol {\mathfrak {t}}=({\textbf {t}}_1,\ldots , {\textbf {t}}_{\ell })\in {\Bbb R}^{\ell d}$
. Later, Solomyak [Reference Solomyak47] pointed out that the bound
$\boldsymbol {\mathfrak {t}}=({\textbf {t}}_1,\ldots , {\textbf {t}}_{\ell })\in {\Bbb R}^{\ell d}$
. Later, Solomyak [Reference Solomyak47] pointed out that the bound
![]() $1/3$
in (1.9) can be replaced by
$1/3$
in (1.9) can be replaced by
![]() $1/2$
. By an observation of Edgar [Reference Edgar12],
$1/2$
. By an observation of Edgar [Reference Edgar12],
![]() $1/2$
is optimal. Under the same assumption that
$1/2$
is optimal. Under the same assumption that
Jordan, Pollicott and Simon [Reference Jordan, Pollicott and Simon32] showed that the translational family
![]() $(\mathcal F^{\boldsymbol {\mathfrak {t}}})_{\boldsymbol {\mathfrak {t}}\in {\Bbb R}^{\ell d}}$
satisfies the self-affine transversality condition. It was pointed out in [Reference Bárány, Simon and Solomyak3, Theorem 9.1.2] that the assumption (1.10) can by further replaced by a slightly more general condition
$(\mathcal F^{\boldsymbol {\mathfrak {t}}})_{\boldsymbol {\mathfrak {t}}\in {\Bbb R}^{\ell d}}$
satisfies the self-affine transversality condition. It was pointed out in [Reference Bárány, Simon and Solomyak3, Theorem 9.1.2] that the assumption (1.10) can by further replaced by a slightly more general condition
![]() $\max _{i\neq j}(\|A_i\|+\|A_j\|)<1$
.
$\max _{i\neq j}(\|A_i\|+\|A_j\|)<1$
.
We remark that Theorem 1.6 also extends the results of Simon, Solomyak and Urbański ([Reference Simon, Solomyak and Urbański45, Proposition 7.1], [Reference Simon, Solomyak and Urbański46, Corollary 7.3]) for translational families of
![]() $C^{1+\alpha }$
conformal IFSs on
$C^{1+\alpha }$
conformal IFSs on
![]() ${\Bbb R}$
. It is worth pointing out that for every
${\Bbb R}$
. It is worth pointing out that for every
![]() $C^1$
conformal IFS satisfying the open set condition (or
$C^1$
conformal IFS satisfying the open set condition (or
![]() $C^1$
conformal expanding map), the dimension of its attractor (or repeller) satisfies the Bowen–Ruelle formula, and is equal to the singularity dimension; meanwhile, the dimension of ergodic invariant measures on the attractor (repeller) is given by the Lyapunov dimension (see [Reference Bowen7, Reference Gatzouras and Peres25, Reference Patzschke39, Reference Ruelle44]).
$C^1$
conformal expanding map), the dimension of its attractor (or repeller) satisfies the Bowen–Ruelle formula, and is equal to the singularity dimension; meanwhile, the dimension of ergodic invariant measures on the attractor (repeller) is given by the Lyapunov dimension (see [Reference Bowen7, Reference Gatzouras and Peres25, Reference Patzschke39, Reference Ruelle44]).
The paper is organized as follows. In §2, we give some preliminaries, including the variational principle for sub-additive topological pressure, and the definitions and properties of singularity dimension and Lyapunov dimension. In §3, we prove Theorem 1.2. The proof of Theorem 1.6 is rather long and will be given in §§4–7, where we divide the whole proof into three different parts, by considering the conditions (i)–(iii) in Theorem 1.6 separately.
2 Preliminaries
2.1 Variational principle for sub-additive pressure
In order to define the singularity and Lyapunov dimensions, we require some elements from the sub-additive thermodynamic formalism.
Let
![]() $(\Sigma ,\sigma )$
be the one-sided full shift over the alphabet
$(\Sigma ,\sigma )$
be the one-sided full shift over the alphabet
![]() $\{1,\ldots , \ell \}$
. That is,
$\{1,\ldots , \ell \}$
. That is,
![]() $\Sigma =\{1,\ldots , \ell \}^{\Bbb N}$
, which is endowed with the product topology, and
$\Sigma =\{1,\ldots , \ell \}^{\Bbb N}$
, which is endowed with the product topology, and
![]() $\sigma :\Sigma \to \Sigma $
is the left shift defined by
$\sigma :\Sigma \to \Sigma $
is the left shift defined by
![]() $(x_i)_{i=1}^{\infty }\mapsto (x_{i+1})_{i=1}^{\infty }$
. Write
$(x_i)_{i=1}^{\infty }\mapsto (x_{i+1})_{i=1}^{\infty }$
. Write
![]() $\Sigma _n=\{1,\ldots , \ell \}^n$
for
$\Sigma _n=\{1,\ldots , \ell \}^n$
for
![]() $n\geq 0$
, with the convention
$n\geq 0$
, with the convention
![]() $\Sigma _0=\{\varepsilon \}$
, where
$\Sigma _0=\{\varepsilon \}$
, where
![]() $\varepsilon $
stands for the empty word. Set
$\varepsilon $
stands for the empty word. Set
![]() $\Sigma _*=\bigcup _{n=0}^{\infty } \Sigma _n$
. For
$\Sigma _*=\bigcup _{n=0}^{\infty } \Sigma _n$
. For
![]() $x=(x_i)_{i=1}^{\infty }\in \Sigma $
and
$x=(x_i)_{i=1}^{\infty }\in \Sigma $
and
![]() $n\in {\Bbb N}$
, write
$n\in {\Bbb N}$
, write
![]() $x|n=x_1\ldots x_n$
.
$x|n=x_1\ldots x_n$
.
Let
![]() $C(\Sigma )$
denote the set of real-valued continuous functions on
$C(\Sigma )$
denote the set of real-valued continuous functions on
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $\mathcal {G}=\{g_n\}_{n=1}^{\infty }$
be a sub-additive potential on
$\mathcal {G}=\{g_n\}_{n=1}^{\infty }$
be a sub-additive potential on
![]() $\Sigma $
, that is,
$\Sigma $
, that is,
![]() $g_n\in C(\Sigma )$
for all
$g_n\in C(\Sigma )$
for all
![]() $n\geq 1$
such that
$n\geq 1$
such that
The topological pressure of
![]() $\mathcal G$
is defined by
$\mathcal G$
is defined by
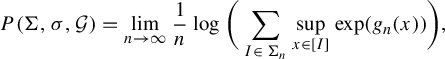 $$ \begin{align} P(\Sigma,\sigma, \mathcal G)= \lim_{n\to\infty} \frac{1}{n}\log\bigg( \sum_{I\in\, \Sigma_n} \sup_{x\in [I]} \exp(g_n(x)) \bigg), \end{align} $$
$$ \begin{align} P(\Sigma,\sigma, \mathcal G)= \lim_{n\to\infty} \frac{1}{n}\log\bigg( \sum_{I\in\, \Sigma_n} \sup_{x\in [I]} \exp(g_n(x)) \bigg), \end{align} $$
where
![]() $[I]:=\{x\in \Sigma :\; x|n=I\}$
for
$[I]:=\{x\in \Sigma :\; x|n=I\}$
for
![]() $I\in \Sigma _n$
. The limit can be seen to exist by using a standard sub-additivity argument.
$I\in \Sigma _n$
. The limit can be seen to exist by using a standard sub-additivity argument.
If the potential
![]() $\mathcal G$
is additive, that is,
$\mathcal G$
is additive, that is,
![]() $g_n=\sum _{k=0}^{n-1}g\circ \sigma ^k$
for some
$g_n=\sum _{k=0}^{n-1}g\circ \sigma ^k$
for some
![]() $g\in C(\Sigma )$
, then
$g\in C(\Sigma )$
, then
![]() $P(\Sigma , \sigma , \mathcal G)$
recovers the classical topological pressure
$P(\Sigma , \sigma , \mathcal G)$
recovers the classical topological pressure
![]() $P(\Sigma , \sigma , g)$
of g (see e.g. [Reference Walters49]).
$P(\Sigma , \sigma , g)$
of g (see e.g. [Reference Walters49]).
Let
![]() $\mathcal {M}(\Sigma ,\sigma )$
denote the set of
$\mathcal {M}(\Sigma ,\sigma )$
denote the set of
![]() $\sigma $
-invariant Borel probability measures on
$\sigma $
-invariant Borel probability measures on
![]() $\Sigma $
. For
$\Sigma $
. For
![]() $\mu \in \mathcal {M}(\Sigma ,\sigma )$
, let
$\mu \in \mathcal {M}(\Sigma ,\sigma )$
, let
![]() $h_{\mu }(\sigma )$
denote the measure-theoretic entropy of
$h_{\mu }(\sigma )$
denote the measure-theoretic entropy of
![]() $\mu $
(cf. [Reference Walters49]). Moreover, for
$\mu $
(cf. [Reference Walters49]). Moreover, for
![]() $\mu \in \mathcal M(\Sigma , \sigma )$
, by sub-additivity,
$\mu \in \mathcal M(\Sigma , \sigma )$
, by sub-additivity,
See e.g. [Reference Walters49, Theorem 10.1]. We call
![]() $\mathcal {G}_*(\mu )$
the Lyapunov exponent of
$\mathcal {G}_*(\mu )$
the Lyapunov exponent of
![]() $\mathcal {G}$
with respect to
$\mathcal {G}$
with respect to
![]() $\mu $
.
$\mu $
.
The following variational principle for the topological pressure of sub-additive potentials generalizes the classical variational principle for additive potentials [Reference Ruelle43, Reference Walters48].
Theorem 2.1. [Reference Cao, Feng and Huang8]
Let
![]() $\mathcal {G}=\{g_n\}_{n=1}^{\infty }$
be a sub-additive potential on
$\mathcal {G}=\{g_n\}_{n=1}^{\infty }$
be a sub-additive potential on
![]() $(\Sigma ,\sigma )$
. Then
$(\Sigma ,\sigma )$
. Then
Although in [Reference Cao, Feng and Huang8] this is proved for sub-additive potentials on an arbitrary continuous dynamical system on a compact space, we state it only for shift spaces. Particular cases of the above result, under stronger assumptions on the potentials, were previously obtained by many authors, see for example [Reference Barreira4, Reference Falconer14, Reference Feng20, Reference Feng and Lau22, Reference Käenmäki34, Reference Mummert38] and references therein.
Measures that achieve the supremum in (2.4) are called equilibrium measures for the potential
![]() ${\mathcal G}$
. There exists at least one ergodic equilibrium measure; see e.g. [Reference Feng21, Proposition 3.5] and the remark there.
${\mathcal G}$
. There exists at least one ergodic equilibrium measure; see e.g. [Reference Feng21, Proposition 3.5] and the remark there.
2.2 Singularity dimension and Lyapunov dimension with respect to
 $C^1$
IFSs
$C^1$
IFSs
In this subsection, we define the singularity and Lyapunov dimensions with respect to
![]() $C^1$
IFSs.
$C^1$
IFSs.
Let
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
![]() $C^1$
IFS on a compact set
$C^1$
IFS on a compact set
![]() $Z\subset {\Bbb R}^d$
and let K denote the attractor of
$Z\subset {\Bbb R}^d$
and let K denote the attractor of
![]() $\mathcal F$
(cf. §1). Let
$\mathcal F$
(cf. §1). Let
![]() $(\Sigma ,\sigma )$
be the one-sided full shift over the alphabet
$(\Sigma ,\sigma )$
be the one-sided full shift over the alphabet
![]() $\{1,\ldots , \ell \}$
and let
$\{1,\ldots , \ell \}$
and let
![]() $\Pi : \Sigma \to K$
be the coding map defined as in (1.2).
$\Pi : \Sigma \to K$
be the coding map defined as in (1.2).
Let
![]() ${\Bbb R}^{d\times d}$
denote the collection of
${\Bbb R}^{d\times d}$
denote the collection of
![]() $d\times d$
real matrices. For
$d\times d$
real matrices. For
![]() $T\in {\Bbb R}^{d\times d}$
, let
$T\in {\Bbb R}^{d\times d}$
, let
denote the singular values of T. Following [Reference Falconer13], for
![]() $s\geq 0$
, we define the singular value function
$s\geq 0$
, we define the singular value function
![]() $\phi ^s:\; {\Bbb R}^{d \times d}\to [0,\infty )$
as
$\phi ^s:\; {\Bbb R}^{d \times d}\to [0,\infty )$
as
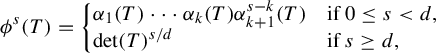 $$ \begin{align} \phi^s(T)=\left\{ \begin{array}{@{}ll} \alpha_1(T)\cdots \alpha_k(T) \alpha_{k+1}^{s-k}(T) & \text{if }0\leq s< d,\\ \det(T)^{s/d} & \text{if } s\geq d, \end{array} \right. \end{align} $$
$$ \begin{align} \phi^s(T)=\left\{ \begin{array}{@{}ll} \alpha_1(T)\cdots \alpha_k(T) \alpha_{k+1}^{s-k}(T) & \text{if }0\leq s< d,\\ \det(T)^{s/d} & \text{if } s\geq d, \end{array} \right. \end{align} $$
where
![]() $k=[s]$
is the integral part of s. Here we make the convention that
$k=[s]$
is the integral part of s. Here we make the convention that
![]() $0^0=1$
. The following result on
$0^0=1$
. The following result on
![]() $\phi ^s$
is well known; see e.g. [Reference Falconer13].
$\phi ^s$
is well known; see e.g. [Reference Falconer13].
Lemma 2.2.
-
(i)
 $\phi ^s(ST)\leq \phi ^s(S)\phi ^s(T)$
for all
$\phi ^s(ST)\leq \phi ^s(S)\phi ^s(T)$
for all
 $S, T\in {\Bbb R}^{d\times d}$
and
$S, T\in {\Bbb R}^{d\times d}$
and
 $s\geq 0$
.
$s\geq 0$
. -
(ii)
 $\phi ^{s+t}(T)\leq \phi ^s(T)\|T\|^t$
for all
$\phi ^{s+t}(T)\leq \phi ^s(T)\|T\|^t$
for all
 $T\in {\Bbb R}^{d\times d}$
,
$T\in {\Bbb R}^{d\times d}$
,
 $s,t\geq 0$
.
$s,t\geq 0$
.
For a differentiable mapping
![]() $f:\; U\subset {\Bbb R}^d\to {\Bbb R}^d$
, let
$f:\; U\subset {\Bbb R}^d\to {\Bbb R}^d$
, let
![]() $D_zf$
denote the differential of f at
$D_zf$
denote the differential of f at
![]() $z\in U$
. Sometimes we also write
$z\in U$
. Sometimes we also write
![]() $f'(z)$
for
$f'(z)$
for
![]() $D_zf$
, and also call
$D_zf$
, and also call
![]() $D_zf$
the Jacobian matrix of f at z. Below we introduce the concepts of singularity and Lyapunov dimensions.
$D_zf$
the Jacobian matrix of f at z. Below we introduce the concepts of singularity and Lyapunov dimensions.
Definition 2.3. The singularity dimension of
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
, written as
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
, written as
![]() $\dim _S\mathcal F$
, is the unique non-negative value s for which
$\dim _S\mathcal F$
, is the unique non-negative value s for which
where
![]() $\mathcal G^s=\{g_n^s\}_{n=1}^{\infty }$
is the sub-additive potential on
$\mathcal G^s=\{g_n^s\}_{n=1}^{\infty }$
is the sub-additive potential on
![]() $\Sigma $
defined by
$\Sigma $
defined by
with
![]() $f_{x|n}:=f_{x_1}\circ \cdots \circ f_{x_n}$
for
$f_{x|n}:=f_{x_1}\circ \cdots \circ f_{x_n}$
for
![]() $x=(x_n)_{n=1}^{\infty }$
.
$x=(x_n)_{n=1}^{\infty }$
.
Definition 2.4. Let
![]() $\mu $
be a
$\mu $
be a
![]() $\sigma $
-invariant Borel probability measure on
$\sigma $
-invariant Borel probability measure on
![]() $\Sigma $
. The Lyapunov dimension of
$\Sigma $
. The Lyapunov dimension of
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
, written as
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
, written as
![]() $\dim _{\mathrm {L}, {\mathcal F}} \mu $
, is the unique non-negative value s for which
$\dim _{\mathrm {L}, {\mathcal F}} \mu $
, is the unique non-negative value s for which
where
![]() $\mathcal G^s=\{g^s_n\}_{n=1}^{\infty }$
is defined as in (2.6) and
$\mathcal G^s=\{g^s_n\}_{n=1}^{\infty }$
is defined as in (2.6) and
![]() $\mathcal G^s_*(\mu ):=\lim _{n\to \infty } ({1}/{n})\int g^s_n\; d\mu $
.
$\mathcal G^s_*(\mu ):=\lim _{n\to \infty } ({1}/{n})\int g^s_n\; d\mu $
.
Remark 2.5.
-
(i) It is not hard to show that there exist
 $a<b<0$
such that for all
$a<b<0$
such that for all $$ \begin{align*}nsa\leq g_n^s(x)\leq ns b,\quad g_n^{s+t}(x)\leq g_n^s(x)+ntb \end{align*} $$
$$ \begin{align*}nsa\leq g_n^s(x)\leq ns b,\quad g_n^{s+t}(x)\leq g_n^s(x)+ntb \end{align*} $$
 $x\in \Sigma $
,
$x\in \Sigma $
,
 $n\in {\Bbb N}$
and
$n\in {\Bbb N}$
and
 $s,t\geq 0$
, where
$s,t\geq 0$
, where
 $g_n^s(x)$
is defined as in (2.6). The existence and uniqueness of s in Definitions 2.3–2.4 just follow from this fact.
$g_n^s(x)$
is defined as in (2.6). The existence and uniqueness of s in Definitions 2.3–2.4 just follow from this fact.
-
(ii) The concept of singularity dimension was first introduced by Falconer [Reference Falconer13, Reference Falconer15]; see also [Reference Käenmäki and Vilppolainen35]. It is also called affinity dimension in the case when the IFS
 $\{f_i\}_{i=1}^{\ell }$
is affine, that is, each map
$\{f_i\}_{i=1}^{\ell }$
is affine, that is, each map
 $f_i$
is affine.
$f_i$
is affine. -
(iii) The definition of Lyapunov dimension of invariant measures with respect to an IFS presented above was adopted from [Reference Jordan and Pollicott31]. It is a generalization of that given in [Reference Jordan, Pollicott and Simon32] for affine IFSs.
The following result describes the relation between the singularity dimension and the Lyapunov dimension.
Lemma 2.6. Let
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
![]() $C^1$
IFS on a compact subset Z of
$C^1$
IFS on a compact subset Z of
![]() ${\Bbb R}^d$
. Suppose
${\Bbb R}^d$
. Suppose
![]() $\theta \in (0,1)$
is a common Lipschitz constant for
$\theta \in (0,1)$
is a common Lipschitz constant for
![]() $f_1,\ldots , f_{\ell }$
. That is,
$f_1,\ldots , f_{\ell }$
. That is,
Then the following properties hold.
-
(i)
 $\dim _S\mathcal F=\sup \{\dim _{L,\mathcal F}\mu :\; \mu \in \mathcal M(\Sigma ,\sigma )\}$
. The supremum is attained by at least one ergodic measure.
$\dim _S\mathcal F=\sup \{\dim _{L,\mathcal F}\mu :\; \mu \in \mathcal M(\Sigma ,\sigma )\}$
. The supremum is attained by at least one ergodic measure. -
(ii)
 $\dim _S\mathcal F\leq ({\log \ell }/{\log (1/\theta )})$
.
$\dim _S\mathcal F\leq ({\log \ell }/{\log (1/\theta )})$
.
Proof Since
![]() $\theta $
is a common Lipschitz constant for
$\theta $
is a common Lipschitz constant for
![]() $f_1,\ldots , f_{\ell }$
,
$f_1,\ldots , f_{\ell }$
,
![]() $\|D_zf_i\|\leq \theta $
for each
$\|D_zf_i\|\leq \theta $
for each
![]() $1\leq i\leq \ell $
and
$1\leq i\leq \ell $
and
![]() $z\in Z$
. It follows from Lemma 2.2(ii) that for
$z\in Z$
. It follows from Lemma 2.2(ii) that for
![]() $s_2>s_1\geq 0$
,
$s_2>s_1\geq 0$
,
from which we see that
Hence
![]() $P(\Sigma , \sigma , \mathcal G^s)$
is strictly decreasing in s.
$P(\Sigma , \sigma , \mathcal G^s)$
is strictly decreasing in s.
Now let
![]() $\mu \in \mathcal M(\Sigma ,\sigma )$
. Write
$\mu \in \mathcal M(\Sigma ,\sigma )$
. Write
![]() $s=\dim _{L,\mathcal F}\mu $
. Then
$s=\dim _{L,\mathcal F}\mu $
. Then
![]() $h_{\mu }(\sigma )+\mathcal G^s_*(\mu )=0$
. Applying Theorem 2.1 to the sub-additive potential
$h_{\mu }(\sigma )+\mathcal G^s_*(\mu )=0$
. Applying Theorem 2.1 to the sub-additive potential
![]() $\mathcal G^s$
yields that
$\mathcal G^s$
yields that
![]() $P(\Sigma , \sigma , \mathcal G^s)\geq 0$
. Hence
$P(\Sigma , \sigma , \mathcal G^s)\geq 0$
. Hence
![]() $\dim _S\mathcal F\geq s=\dim _{L,\mathcal F}\mu $
. It follows that
$\dim _S\mathcal F\geq s=\dim _{L,\mathcal F}\mu $
. It follows that
To show that equality holds, write
![]() $s'=\dim _S\mathcal F$
. Let
$s'=\dim _S\mathcal F$
. Let
![]() $\nu $
be an ergodic equilibrium measure for the potential
$\nu $
be an ergodic equilibrium measure for the potential
![]() $\mathcal G^{s'}$
. Then
$\mathcal G^{s'}$
. Then
which implies that
![]() $\dim _{L, \mathcal F}\nu =s'$
. That is,
$\dim _{L, \mathcal F}\nu =s'$
. That is,
![]() $\dim _{L, \mathcal F}\nu =\dim _S\mathcal F$
. This completes the proof of (i).
$\dim _{L, \mathcal F}\nu =\dim _S\mathcal F$
. This completes the proof of (i).
To see (ii), notice that
![]() $\phi ^{s'}(D_{\Pi \sigma ^n x} f_{x|n})\leq \theta ^{ns'}$
for all
$\phi ^{s'}(D_{\Pi \sigma ^n x} f_{x|n})\leq \theta ^{ns'}$
for all
![]() $x\in \Sigma $
and
$x\in \Sigma $
and
![]() $n\in {\Bbb N}$
. It follows from the definition of
$n\in {\Bbb N}$
. It follows from the definition of
![]() $P(\Sigma , \sigma , \mathcal G^{s'})$
that
$P(\Sigma , \sigma , \mathcal G^{s'})$
that
from which we obtain
![]() $s'\leq ({\log \ell }/{\log (1/\theta )})$
. This completes the proof of (ii).
$s'\leq ({\log \ell }/{\log (1/\theta )})$
. This completes the proof of (ii).
For a
![]() $\sigma $
-invariant ergodic measure
$\sigma $
-invariant ergodic measure
![]() $\mu $
on
$\mu $
on
![]() $\Sigma $
, let
$\Sigma $
, let
![]() $\Pi _*\mu $
denote the push-forward of
$\Pi _*\mu $
denote the push-forward of
![]() $\mu $
by
$\mu $
by
![]() $\Pi $
. In the following, we present the main result obtained in the first part [Reference Feng and Simon24] of our study on the dimension of
$\Pi $
. In the following, we present the main result obtained in the first part [Reference Feng and Simon24] of our study on the dimension of
![]() $C^1$
IFSs: the upper box-counting dimension of the attractor of
$C^1$
IFSs: the upper box-counting dimension of the attractor of
![]() $\mathcal F$
is bounded above by the singularity dimension of
$\mathcal F$
is bounded above by the singularity dimension of
![]() $\mathcal F$
, whilst the upper packing dimension of
$\mathcal F$
, whilst the upper packing dimension of
![]() $\Pi _*\mu $
is bounded above by the Lyapunov dimension of
$\Pi _*\mu $
is bounded above by the Lyapunov dimension of
![]() $\mu $
.
$\mu $
.
Theorem 2.7. [Reference Feng and Simon24]
Let
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
be a
![]() $C^1$
IFS with attractor K, and let
$C^1$
IFS with attractor K, and let
![]() $\mu $
be a
$\mu $
be a
![]() $\sigma $
-invariant ergodic measure on
$\sigma $
-invariant ergodic measure on
![]() $\Sigma $
. Then the following properties hold.
$\Sigma $
. Then the following properties hold.
-
(i)
 $\overline {\dim }_B K\leq \dim _S \mathcal F$
.
$\overline {\dim }_B K\leq \dim _S \mathcal F$
. -
(ii)
 $\overline {\dim }_P \Pi _*\mu \leq \dim _{L,\mathcal F}(\mu )$
.
$\overline {\dim }_P \Pi _*\mu \leq \dim _{L,\mathcal F}(\mu )$
.
3 The proof of Theorem 1.2
In this section, we prove Theorem 1.2. A key part of the proof is the following proposition.
Proposition 3.1. Assume that
![]() $\mathcal F^t$
,
$\mathcal F^t$
,
![]() $t\in {\Omega }$
, satisfies the GTC with respect to a locally finite Borel measure
$t\in {\Omega }$
, satisfies the GTC with respect to a locally finite Borel measure
![]() $\eta $
on
$\eta $
on
![]() ${\Omega }$
. Let
${\Omega }$
. Let
![]() $\mu $
be a
$\mu $
be a
![]() $\sigma $
-invariant ergodic measure on
$\sigma $
-invariant ergodic measure on
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $t_0\in {\Omega }$
and
$t_0\in {\Omega }$
and
![]() $0<\delta <\delta _0$
, where
$0<\delta <\delta _0$
, where
![]() $\delta _0$
is given as in Definition 1.1, Then the following properties hold.
$\delta _0$
is given as in Definition 1.1, Then the following properties hold.
-
(i) For
 $\eta $
-a.e.
$\eta $
-a.e.
 $t\in B(t_0,\delta )$
, (3.1)where
$t\in B(t_0,\delta )$
, (3.1)where $$ \begin{align} \underline{\dim}_H\Pi^t_*\mu\geq \min\{d, d_{\mu}(t_0)\}-\frac{\psi(\delta)}{\log (1/\theta)}, \end{align} $$
$$ \begin{align} \underline{\dim}_H\Pi^t_*\mu\geq \min\{d, d_{\mu}(t_0)\}-\frac{\psi(\delta)}{\log (1/\theta)}, \end{align} $$
 $\psi (\cdot )$
is given as in Definition 1.1, and
$\psi (\cdot )$
is given as in Definition 1.1, and
 $\theta $
is given as in (1.3).
$\theta $
is given as in (1.3).
-
(ii) If
 $d_{\mu }(t_0)>d+({\psi (\delta )}/{\log (1/\theta )})$
, then
$d_{\mu }(t_0)>d+({\psi (\delta )}/{\log (1/\theta )})$
, then
 $\Pi ^t_*\mu \ll \mathcal L_d$
for
$\Pi ^t_*\mu \ll \mathcal L_d$
for
 $\eta $
-a.e.
$\eta $
-a.e.
 $t\in B(t_0,\delta )$
.
$t\in B(t_0,\delta )$
.
The proof of the above proposition is adapted from an argument used in [Reference Jordan, Pollicott and Simon32, Propositions 4.3 and 4.4]. For the reader’s convenience, we include a full proof. We begin with the following.
Lemma 3.2. Assume that
![]() $(\mathcal F^t)_{t\in {\Omega }}$
satisfies the GTC with respect to a locally finite Borel measure
$(\mathcal F^t)_{t\in {\Omega }}$
satisfies the GTC with respect to a locally finite Borel measure
![]() $\eta $
on
$\eta $
on
![]() ${\Omega }$
. Let s be non-integral with
${\Omega }$
. Let s be non-integral with
![]() $0<s<d$
. Let
$0<s<d$
. Let
![]() $t_0\in {\Omega }$
and
$t_0\in {\Omega }$
and
![]() $0<\delta <\delta _0$
, where
$0<\delta <\delta _0$
, where
![]() $\delta _0$
is given as in Definition 1.1. Then there exists a number
$\delta _0$
is given as in Definition 1.1. Then there exists a number
![]() $c>0$
, dependent on s and
$c>0$
, dependent on s and
![]() $\delta $
, such that for all distinct
$\delta $
, such that for all distinct
![]() $\mathbf {i},\mathbf {j}\in \Sigma $
,
$\mathbf {i},\mathbf {j}\in \Sigma $
,
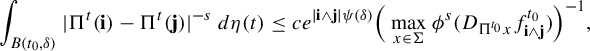 $$ \begin{align} \int_{B(t_0,\delta)} |\Pi^t({\textbf{i}})-\Pi^t(\mathbf{j}) |^{-s} \;d\eta(t)\leq c e^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} \Big( \max_{x\in \Sigma} \phi^s (D_{\Pi^{t_0} x} f^{t_0}_{\mathbf{i}\wedge \mathbf{j}})\Big)^{-1}, \end{align} $$
$$ \begin{align} \int_{B(t_0,\delta)} |\Pi^t({\textbf{i}})-\Pi^t(\mathbf{j}) |^{-s} \;d\eta(t)\leq c e^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} \Big( \max_{x\in \Sigma} \phi^s (D_{\Pi^{t_0} x} f^{t_0}_{\mathbf{i}\wedge \mathbf{j}})\Big)^{-1}, \end{align} $$
where
![]() $\psi (\cdot )$
is given as in Definition 1.1.
$\psi (\cdot )$
is given as in Definition 1.1.
Proof Take
![]() $y\in \Sigma $
so that
$y\in \Sigma $
so that
![]() $ \phi ^s (D_{\Pi ^{t_0} y} f^{t_0}_{\mathbf {i}\wedge \mathbf {j}})= \max _{x\in \Sigma } \phi ^s (D_{\Pi ^{t_0} x} f^t_{\mathbf {i}\wedge \mathbf {j}}). $
Let k be the unique integer such that
$ \phi ^s (D_{\Pi ^{t_0} y} f^{t_0}_{\mathbf {i}\wedge \mathbf {j}})= \max _{x\in \Sigma } \phi ^s (D_{\Pi ^{t_0} x} f^t_{\mathbf {i}\wedge \mathbf {j}}). $
Let k be the unique integer such that
![]() $s\in (k, k+1)$
. Clearly
$s\in (k, k+1)$
. Clearly
![]() $k\in \{0,1,\ldots , d-1\}$
. For convenience, write
$k\in \{0,1,\ldots , d-1\}$
. For convenience, write
where
![]() $\phi ^s(\cdot )$
stands for the singular value function (see (2.5) for the definition). A direct check shows that
$\phi ^s(\cdot )$
stands for the singular value function (see (2.5) for the definition). A direct check shows that
Observe that
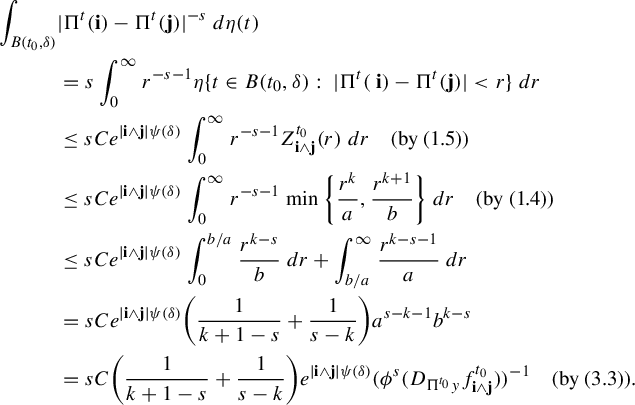 $$ \begin{align*} \int_{B(t_0,\delta)} & |\Pi^t({\textbf{i}})-\Pi^t(\mathbf{j}) |^{-s} \;d\eta(t)\\ &=s\int_0^{\infty} r^{-s-1} \eta \{t\in B(t_0,\delta):\; |\Pi^t({\textbf{ i}})-\Pi^t({\textbf{j}}) |< r\}\; dr\\ &\leq sCe^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} \int_0^{\infty} r^{-s-1} Z^{t_0}_{\mathbf{i}\wedge \mathbf{j}}(r) \; dr \quad (\text{by (1.5)})\\ &\leq sCe^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} \int_0^{\infty} r^{-s-1} \min\bigg\{ \frac{r^k}{a}, \frac{r^{k+1}}{b} \bigg\} \; dr \quad (\text{by (1.4)})\\ &\leq sCe^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} \int_0^{b/a} \frac{r^{k-s}}{b} \;dr+ \int_{b/a}^{\infty} \frac{r^{k-s-1}}{a}\; dr\\ &=sCe^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} \bigg(\frac{1}{k+1-s}+\frac{1}{s-k}\bigg)a^{s-k-1}b^{k-s}\\ &=sC\bigg(\frac{1}{k+1-s}+\frac{1}{s-k}\bigg)e^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} (\phi^s (D_{\Pi^{t_0} y}f^{t_0}_{\mathbf{i}\wedge \mathbf{ j}}))^{-1}\quad (\text{by (3.3))}. \end{align*} $$
$$ \begin{align*} \int_{B(t_0,\delta)} & |\Pi^t({\textbf{i}})-\Pi^t(\mathbf{j}) |^{-s} \;d\eta(t)\\ &=s\int_0^{\infty} r^{-s-1} \eta \{t\in B(t_0,\delta):\; |\Pi^t({\textbf{ i}})-\Pi^t({\textbf{j}}) |< r\}\; dr\\ &\leq sCe^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} \int_0^{\infty} r^{-s-1} Z^{t_0}_{\mathbf{i}\wedge \mathbf{j}}(r) \; dr \quad (\text{by (1.5)})\\ &\leq sCe^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} \int_0^{\infty} r^{-s-1} \min\bigg\{ \frac{r^k}{a}, \frac{r^{k+1}}{b} \bigg\} \; dr \quad (\text{by (1.4)})\\ &\leq sCe^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} \int_0^{b/a} \frac{r^{k-s}}{b} \;dr+ \int_{b/a}^{\infty} \frac{r^{k-s-1}}{a}\; dr\\ &=sCe^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} \bigg(\frac{1}{k+1-s}+\frac{1}{s-k}\bigg)a^{s-k-1}b^{k-s}\\ &=sC\bigg(\frac{1}{k+1-s}+\frac{1}{s-k}\bigg)e^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)} (\phi^s (D_{\Pi^{t_0} y}f^{t_0}_{\mathbf{i}\wedge \mathbf{ j}}))^{-1}\quad (\text{by (3.3))}. \end{align*} $$
This proves (3.2) by setting
![]() $c=sC(({1}/({k+1-s}))+({1}/({s-k})))$
.
$c=sC(({1}/({k+1-s}))+({1}/({s-k})))$
.
Proof of Proposition 3.1 Fix
![]() $t_0\in {\Omega }$
and
$t_0\in {\Omega }$
and
![]() $\delta \in (0,\delta _0)$
. We first prove part (i). Let
$\delta \in (0,\delta _0)$
. We first prove part (i). Let
![]() $\epsilon>0$
and let s be non-integral so that
$\epsilon>0$
and let s be non-integral so that
To show that (3.1) holds for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in B(t_0,\delta )$
, it suffices to show that
$t\in B(t_0,\delta )$
, it suffices to show that
For this purpose, we write
We first prove that
To see this, according to the definition of
![]() $d_{\mu }(t_0)$
(cf. (1.6) and Definition 2.4),
$d_{\mu }(t_0)$
(cf. (1.6) and Definition 2.4),
It follows from (3.8), the Shannon–McMillan–Breiman theorem and Kingman’s sub-additive ergodic theorem (see [Reference Walters49, pp. 93 and 231]) that
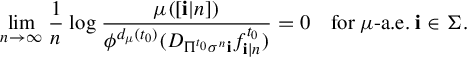 $$ \begin{align} \lim_{n\to \infty}\frac{1}{n}\log \frac{\mu([\mathbf{i}|n])}{\phi^{d_{\mu}(t_0)} (D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n})}=0 \quad \text{for } \mu\text{-a.e.~}\mathbf{i}\in \Sigma. \end{align} $$
$$ \begin{align} \lim_{n\to \infty}\frac{1}{n}\log \frac{\mu([\mathbf{i}|n])}{\phi^{d_{\mu}(t_0)} (D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n})}=0 \quad \text{for } \mu\text{-a.e.~}\mathbf{i}\in \Sigma. \end{align} $$
Observe that for each
![]() $\mathbf {i}\in \Sigma $
and
$\mathbf {i}\in \Sigma $
and
![]() $n\in {\Bbb N}$
,
$n\in {\Bbb N}$
,
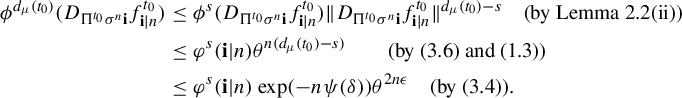 $$ \begin{align*} \phi^{d_{\mu}(t_0)} (D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}) &\leq \phi^{s} (D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}) \|D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}\|^{d_{\mu}(t_0)-s} \quad \text{(by Lemma 2.2(ii))}\\ &\leq \varphi^{s} (\mathbf{i}|n) \theta^{n(d_{\mu}(t_0)-s)}\quad\quad \text{(by (3.6) and (1.3))}\\ &\leq \varphi^s(\mathbf{i}|n) \exp(-n \psi(\delta))\theta^{2n\epsilon} \quad \text{(by (3.4))}. \end{align*} $$
$$ \begin{align*} \phi^{d_{\mu}(t_0)} (D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}) &\leq \phi^{s} (D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}) \|D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}\|^{d_{\mu}(t_0)-s} \quad \text{(by Lemma 2.2(ii))}\\ &\leq \varphi^{s} (\mathbf{i}|n) \theta^{n(d_{\mu}(t_0)-s)}\quad\quad \text{(by (3.6) and (1.3))}\\ &\leq \varphi^s(\mathbf{i}|n) \exp(-n \psi(\delta))\theta^{2n\epsilon} \quad \text{(by (3.4))}. \end{align*} $$
Combining the above inequality with (3.9) yields (3.7).
By (3.7), we may find a countable disjoint collection of Borel subsets
![]() $E_j$
of
$E_j$
of
![]() $\Sigma $
with
$\Sigma $
with
![]() $\mu (\Sigma \backslash \bigcup _{j=1}^{\infty } E_j)=0$
and numbers
$\mu (\Sigma \backslash \bigcup _{j=1}^{\infty } E_j)=0$
and numbers
![]() $c_j>0$
such that
$c_j>0$
such that
where
![]() $\mu _j$
stands for the restriction of
$\mu _j$
stands for the restriction of
![]() $\mu $
to
$\mu $
to
![]() $E_j$
defined by
$E_j$
defined by
![]() $\mu _j(A)=\mu (E_j\cap A)$
. Clearly,
$\mu _j(A)=\mu (E_j\cap A)$
. Clearly,
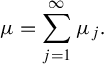 $$ \begin{align} \mu=\sum_{j=1}^{\infty} \mu_j. \end{align} $$
$$ \begin{align} \mu=\sum_{j=1}^{\infty} \mu_j. \end{align} $$
Hence, to prove (3.5), it suffices to show that for each j,
By the potential theoretic characterization of the Hausdorff dimension (see e.g. [Reference Falconer16, Theorem 4.13]), it is enough to show that for each j and
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in B(t_0,\delta )$
,
$t\in B(t_0,\delta )$
,
![]() $\Pi ^t_*\mu _j$
has finite s-energy:
$\Pi ^t_*\mu _j$
has finite s-energy:
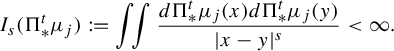 $$ \begin{align*}I_s(\Pi^t_*\mu_j):=\iint \frac{ d \Pi^t_*\mu_j (x)d \Pi^t_*\mu_j (y)}{|x-y|^{s}}<\infty. \end{align*} $$
$$ \begin{align*}I_s(\Pi^t_*\mu_j):=\iint \frac{ d \Pi^t_*\mu_j (x)d \Pi^t_*\mu_j (y)}{|x-y|^{s}}<\infty. \end{align*} $$
Integrating over
![]() $B(t_0,\delta )$
with respect to
$B(t_0,\delta )$
with respect to
![]() $\eta $
and using Fubini’s theorem,
$\eta $
and using Fubini’s theorem,
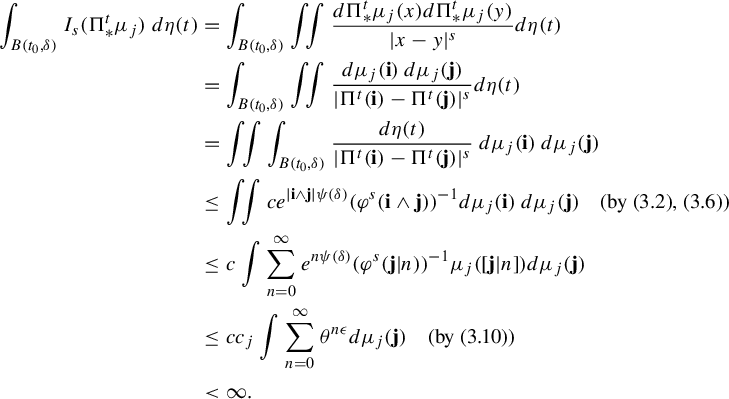 $$ \begin{align*} \int_{B(t_0,\delta)}I_s(\Pi^t_*\mu_j)\; d\eta(t)&=\int_{B(t_0,\delta)} \iint \frac{ d \Pi^t_*\mu_j (x)d \Pi^t_*\mu_j (y)}{|x-y|^{s}} d\eta(t)\\ &=\int_{B(t_0,\delta)} \iint \frac{ d\mu_j (\mathbf{i})\,d \mu_j (\mathbf{j})}{|\Pi^t(\mathbf{i})-\Pi^t(\mathbf{j})|^{s}} d\eta(t)\\ &= \iint \int_{B(t_0,\delta)} \frac{d\eta(t)}{|\Pi^t(\mathbf{i})-\Pi^t(\mathbf{j})|^{s}} \ d\mu_j (\mathbf{i})\,d \mu_j (\mathbf{j})\\ &\leq \iint c e^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)}(\varphi^s(\mathbf{i}\wedge \mathbf{j}))^{-1} d\mu_j (\mathbf{i})\,d \mu_j (\mathbf{ j})\quad \text{(by (3.2), (3.6))}\\ &\leq c\int \sum_{n=0}^{\infty} e^{n\psi(\delta)} (\varphi^s(\mathbf{j}|n))^{-1} \mu_j([\mathbf{j}|n])d \mu_j (\mathbf{j})\\ &\leq cc_j\int \sum_{n=0}^{\infty} \theta^{n\epsilon} d \mu_j (\mathbf{j})\quad \text{(by (3.10))}\\ &<\infty. \end{align*} $$
$$ \begin{align*} \int_{B(t_0,\delta)}I_s(\Pi^t_*\mu_j)\; d\eta(t)&=\int_{B(t_0,\delta)} \iint \frac{ d \Pi^t_*\mu_j (x)d \Pi^t_*\mu_j (y)}{|x-y|^{s}} d\eta(t)\\ &=\int_{B(t_0,\delta)} \iint \frac{ d\mu_j (\mathbf{i})\,d \mu_j (\mathbf{j})}{|\Pi^t(\mathbf{i})-\Pi^t(\mathbf{j})|^{s}} d\eta(t)\\ &= \iint \int_{B(t_0,\delta)} \frac{d\eta(t)}{|\Pi^t(\mathbf{i})-\Pi^t(\mathbf{j})|^{s}} \ d\mu_j (\mathbf{i})\,d \mu_j (\mathbf{j})\\ &\leq \iint c e^{|\mathbf{i}\wedge \mathbf{j}|\psi(\delta)}(\varphi^s(\mathbf{i}\wedge \mathbf{j}))^{-1} d\mu_j (\mathbf{i})\,d \mu_j (\mathbf{ j})\quad \text{(by (3.2), (3.6))}\\ &\leq c\int \sum_{n=0}^{\infty} e^{n\psi(\delta)} (\varphi^s(\mathbf{j}|n))^{-1} \mu_j([\mathbf{j}|n])d \mu_j (\mathbf{j})\\ &\leq cc_j\int \sum_{n=0}^{\infty} \theta^{n\epsilon} d \mu_j (\mathbf{j})\quad \text{(by (3.10))}\\ &<\infty. \end{align*} $$
It follows that
![]() $I_s(\Pi ^t_*\mu _j)<\infty $
for
$I_s(\Pi ^t_*\mu _j)<\infty $
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in B(t_0,\delta )$
. This completes the proof of part (i).
$t\in B(t_0,\delta )$
. This completes the proof of part (i).
Next we prove part (ii). Take a small
![]() $\epsilon>0$
so that
$\epsilon>0$
so that
Then for every
![]() $\mathbf {i}\in \Sigma $
and
$\mathbf {i}\in \Sigma $
and
![]() $n\in {\Bbb N}$
,
$n\in {\Bbb N}$
,
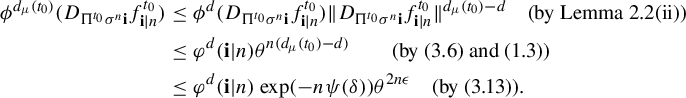 $$ \begin{align*} \phi^{d_{\mu}(t_0)} (D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}) &\leq \phi^{d} (D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}) \|D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}\|^{d_{\mu}(t_0)-d} \quad \text{(by Lemma 2.2(ii))}\\ &\leq \varphi^{d} (\mathbf{i}|n) \theta^{n(d_{\mu}(t_0)-d)}\quad\quad \text{(by (3.6) and (1.3))}\\ &\leq \varphi^d(\mathbf{i}|n) \exp(-n \psi(\delta))\theta^{2n\epsilon} \quad \text{(by (3.13))}. \end{align*} $$
$$ \begin{align*} \phi^{d_{\mu}(t_0)} (D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}) &\leq \phi^{d} (D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}) \|D_{\Pi^{t_0}\sigma^n\mathbf{i}} f^{t_0}_{\mathbf{i}|n}\|^{d_{\mu}(t_0)-d} \quad \text{(by Lemma 2.2(ii))}\\ &\leq \varphi^{d} (\mathbf{i}|n) \theta^{n(d_{\mu}(t_0)-d)}\quad\quad \text{(by (3.6) and (1.3))}\\ &\leq \varphi^d(\mathbf{i}|n) \exp(-n \psi(\delta))\theta^{2n\epsilon} \quad \text{(by (3.13))}. \end{align*} $$
Combining the above inequality with (3.9) yields that
Hence, there exist finite positive measures
![]() $\nu _j$
and numbers
$\nu _j$
and numbers
![]() $a_j$
(
$a_j$
(
![]() $j\geq 1)$
such that
$j\geq 1)$
such that
![]() $\mu =\sum _{j=1}^{\infty } \nu _j$
and
$\mu =\sum _{j=1}^{\infty } \nu _j$
and
Since
![]() $\mu =\sum _{j=1}^{\infty } \nu _j$
, to show that
$\mu =\sum _{j=1}^{\infty } \nu _j$
, to show that
![]() $\Pi ^t_*\mu \ll \mathcal L_d$
for
$\Pi ^t_*\mu \ll \mathcal L_d$
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in B(t_0,\delta )$
, it suffices to show that for each j,
$t\in B(t_0,\delta )$
, it suffices to show that for each j,
To this end, fix j. We will follow a standard approach (introduced by Peres and Solomyak in [Reference Peres and Solomyak40]). In particular, it suffices to show that
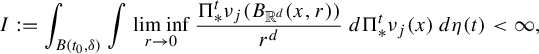 $$ \begin{align*}I:=\int_{B(t_0,\delta)} \int \liminf_{r\to 0} \frac{\Pi^t_*\nu_j(B_{{\Bbb R}^d}(x,r)) }{r^d}\; d\Pi^t_*\nu_j(x)\,d\eta(t) <\infty, \end{align*} $$
$$ \begin{align*}I:=\int_{B(t_0,\delta)} \int \liminf_{r\to 0} \frac{\Pi^t_*\nu_j(B_{{\Bbb R}^d}(x,r)) }{r^d}\; d\Pi^t_*\nu_j(x)\,d\eta(t) <\infty, \end{align*} $$
where
![]() $B_{{\Bbb R}^d}(x,r)$
stands for the closed ball in
$B_{{\Bbb R}^d}(x,r)$
stands for the closed ball in
![]() ${\Bbb R}^d$
centered at x of radius r. Observe that by (1.4) and (3.6),
${\Bbb R}^d$
centered at x of radius r. Observe that by (1.4) and (3.6),
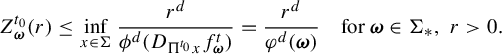 $$ \begin{align} Z^{t_0}_{\boldsymbol{\omega}}(r)\leq \inf_{x\in \Sigma} \frac{r^d}{ \phi^d (D_{\Pi^{t_0} x}f^t_{\boldsymbol{\omega}} ) }=\frac{r^d}{\varphi^d(\boldsymbol{\omega})}\quad \text{for }\boldsymbol{\omega}\in \Sigma_*,\; r>0. \end{align} $$
$$ \begin{align} Z^{t_0}_{\boldsymbol{\omega}}(r)\leq \inf_{x\in \Sigma} \frac{r^d}{ \phi^d (D_{\Pi^{t_0} x}f^t_{\boldsymbol{\omega}} ) }=\frac{r^d}{\varphi^d(\boldsymbol{\omega})}\quad \text{for }\boldsymbol{\omega}\in \Sigma_*,\; r>0. \end{align} $$
Applying Fatou’s Lemma and Fubini’s Theorem,
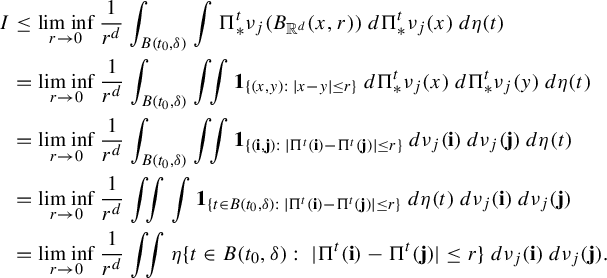 $$ \begin{align*} I&\leq \liminf_{r\to 0}\frac{1}{r^d} \int_{B(t_0,\delta)} \int \Pi^t_*\nu_j(B_{{\Bbb R}^d}(x,r)) \; d\Pi^t_*\nu_j(x)\,d\eta(t)\\ &=\liminf_{r\to 0}\frac{1}{r^d} \int_{B(t_0,\delta)} \iint {\textbf{1}}_{\{ (x,y): \; |x-y|\leq r\}} \; d\Pi^t_*\nu_j(x)\,d\Pi^t_*\nu_j(y)\,d\eta(t)\\ &=\liminf_{r\to 0}\frac{1}{r^d} \int_{B(t_0,\delta)} \iint {\textbf{1}}_{\{(\mathbf{i}, \mathbf{j}):\; |\Pi^t(\mathbf{i})-\Pi^t(\mathbf{j})|\leq r\}} \; d\nu_j(\mathbf{i})\,d\nu_j(\mathbf{j})\,d\eta(t) \\ &=\liminf_{r\to 0}\frac{1}{r^d} \iint \int {\textbf{1}}_{\{ t\in B(t_0,\delta):\; |\Pi^t(\mathbf{i})-\Pi^t(\mathbf{j})|\leq r\}} \; d\eta(t)\,d\nu_j(\mathbf{i})\,d\nu_j(\mathbf{j}) \\ &=\liminf_{r\to 0}\frac{1}{r^d} \iint \eta\{t\in B(t_0,\delta):\; |\Pi^t(\mathbf{i})-\Pi^t(\mathbf{j})|\leq r\} \; d\nu_j(\mathbf{i})\,d\nu_j(\mathbf{j}). \end{align*} $$
$$ \begin{align*} I&\leq \liminf_{r\to 0}\frac{1}{r^d} \int_{B(t_0,\delta)} \int \Pi^t_*\nu_j(B_{{\Bbb R}^d}(x,r)) \; d\Pi^t_*\nu_j(x)\,d\eta(t)\\ &=\liminf_{r\to 0}\frac{1}{r^d} \int_{B(t_0,\delta)} \iint {\textbf{1}}_{\{ (x,y): \; |x-y|\leq r\}} \; d\Pi^t_*\nu_j(x)\,d\Pi^t_*\nu_j(y)\,d\eta(t)\\ &=\liminf_{r\to 0}\frac{1}{r^d} \int_{B(t_0,\delta)} \iint {\textbf{1}}_{\{(\mathbf{i}, \mathbf{j}):\; |\Pi^t(\mathbf{i})-\Pi^t(\mathbf{j})|\leq r\}} \; d\nu_j(\mathbf{i})\,d\nu_j(\mathbf{j})\,d\eta(t) \\ &=\liminf_{r\to 0}\frac{1}{r^d} \iint \int {\textbf{1}}_{\{ t\in B(t_0,\delta):\; |\Pi^t(\mathbf{i})-\Pi^t(\mathbf{j})|\leq r\}} \; d\eta(t)\,d\nu_j(\mathbf{i})\,d\nu_j(\mathbf{j}) \\ &=\liminf_{r\to 0}\frac{1}{r^d} \iint \eta\{t\in B(t_0,\delta):\; |\Pi^t(\mathbf{i})-\Pi^t(\mathbf{j})|\leq r\} \; d\nu_j(\mathbf{i})\,d\nu_j(\mathbf{j}). \end{align*} $$
By (1.5) and (3.16), we obtain that
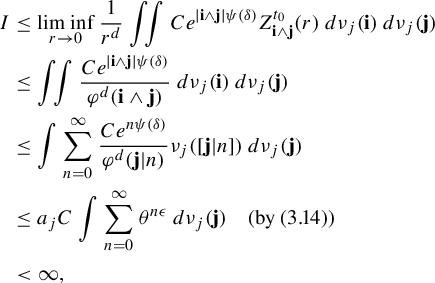 $$ \begin{align*} I &\leq \liminf_{r\to 0}\frac{1}{r^d} \iint C e^{|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)} Z_{{\textbf{i}}\wedge {\textbf{j}}}^{t_0}(r) \; d\nu_j(\mathbf{i})\,d\nu_j(\mathbf{j})\\ &\leq \iint \frac{C e^{|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)}}{\varphi^d(\mathbf{i}\wedge \mathbf{j})} \; d\nu_j(\mathbf{i})\,d\nu_j(\mathbf{j})\\ &\leq \int \sum_{n=0}^{\infty} \frac{C e^{n \psi(\delta)}}{\varphi^d( \mathbf{j}|n)}\nu_j ([\mathbf{j} |n])\; d\nu_j(\mathbf{j})\\ &\leq a_jC\int \sum_{n=0}^{\infty} \theta^{n\epsilon}\; d\nu_j(\mathbf{j}) \quad \text{(by ({3.14}))}\\ &<\infty, \end{align*} $$
$$ \begin{align*} I &\leq \liminf_{r\to 0}\frac{1}{r^d} \iint C e^{|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)} Z_{{\textbf{i}}\wedge {\textbf{j}}}^{t_0}(r) \; d\nu_j(\mathbf{i})\,d\nu_j(\mathbf{j})\\ &\leq \iint \frac{C e^{|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)}}{\varphi^d(\mathbf{i}\wedge \mathbf{j})} \; d\nu_j(\mathbf{i})\,d\nu_j(\mathbf{j})\\ &\leq \int \sum_{n=0}^{\infty} \frac{C e^{n \psi(\delta)}}{\varphi^d( \mathbf{j}|n)}\nu_j ([\mathbf{j} |n])\; d\nu_j(\mathbf{j})\\ &\leq a_jC\int \sum_{n=0}^{\infty} \theta^{n\epsilon}\; d\nu_j(\mathbf{j}) \quad \text{(by ({3.14}))}\\ &<\infty, \end{align*} $$
which completes the proof of part (ii).
Now we are ready to prove Theorem 1.2.
Proof of Theorem 1.2(i) Let
![]() $\mu $
be a
$\mu $
be a
![]() $\sigma $
-invariant ergodic measure on
$\sigma $
-invariant ergodic measure on
![]() $\Sigma $
. We first show that for
$\Sigma $
. We first show that for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in {\Omega }$
,
$t\in {\Omega }$
,
![]() $\Pi ^t_*\mu $
is exact dimensional with dimension equal to
$\Pi ^t_*\mu $
is exact dimensional with dimension equal to
![]() $\min \{d, d_{\mu }(t)\}$
. Recall that
$\min \{d, d_{\mu }(t)\}$
. Recall that
![]() $\overline {\dim }_P\Pi ^t_*\mu \leq \min \{d, d_{\mu }(t)\}$
for each
$\overline {\dim }_P\Pi ^t_*\mu \leq \min \{d, d_{\mu }(t)\}$
for each
![]() $t\in {\Omega }$
(see Theorem 2.7(ii)). Hence, it is sufficient to show that for
$t\in {\Omega }$
(see Theorem 2.7(ii)). Hence, it is sufficient to show that for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in {\Omega }$
,
$t\in {\Omega }$
,
![]() $\underline {\dim }_H \Pi ^t_*\mu \geq \min \{d, d_{\mu }(t)\}$
. Suppose on the contrary that this is false. Then there exist
$\underline {\dim }_H \Pi ^t_*\mu \geq \min \{d, d_{\mu }(t)\}$
. Suppose on the contrary that this is false. Then there exist
![]() $k\in {\Bbb N}$
and
$k\in {\Bbb N}$
and
![]() $A\subset {\Omega }$
with
$A\subset {\Omega }$
with
![]() $\eta (A)>0$
such that
$\eta (A)>0$
such that
Take a number
![]() $\delta \in (0, \delta _0)$
small enough such that
$\delta \in (0, \delta _0)$
small enough such that
Since
![]() ${\Omega }$
is a separable metric space, it has a countable dense subset
${\Omega }$
is a separable metric space, it has a countable dense subset
Notice that by (1.3) and Lemma 2.6,
Due to this fact, for each
![]() $n\in {\Bbb N}$
, we may pick
$n\in {\Bbb N}$
, we may pick
![]() $y_n^*\in B(y_n,\delta /2)$
so that
$y_n^*\in B(y_n,\delta /2)$
so that
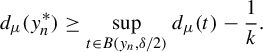 $$ \begin{align} d_{\mu}(y_n^*)\geq \sup_{t\in B(y_n, \delta/2)}d_{\mu}(t)-\frac{1}{k}. \end{align} $$
$$ \begin{align} d_{\mu}(y_n^*)\geq \sup_{t\in B(y_n, \delta/2)}d_{\mu}(t)-\frac{1}{k}. \end{align} $$
Let
![]() $Y^*=\{y_{n}^*:\; n\in {\Bbb N}\}$
. Clearly,
$Y^*=\{y_{n}^*:\; n\in {\Bbb N}\}$
. Clearly,
![]() $Y^*$
is countable. We claim that
$Y^*$
is countable. We claim that
 $$ \begin{align} \sup_{y^*\in B(t, \delta)\cap Y^*} d_{\mu}(y^*)\geq d_{\mu}(t)-\frac1k \quad \text{for all } t\in {\Omega}. \end{align} $$
$$ \begin{align} \sup_{y^*\in B(t, \delta)\cap Y^*} d_{\mu}(y^*)\geq d_{\mu}(t)-\frac1k \quad \text{for all } t\in {\Omega}. \end{align} $$
To see this, let
![]() $t\in {\Omega }$
. Since Y is dense in
$t\in {\Omega }$
. Since Y is dense in
![]() ${\Omega }$
, there exists an integer m such that
${\Omega }$
, there exists an integer m such that
![]() $\rho (y_m, t)\leq \delta /2$
. Then
$\rho (y_m, t)\leq \delta /2$
. Then
Meanwhile, by (3.19),
 $$ \begin{align*}d_{\mu}(y_m^*)\geq \sup_{t'\in B(y_m, \delta/2)}d_{\mu}(t')-\frac{1}{k}\geq d_{\mu}(t)-\frac1k, \end{align*} $$
$$ \begin{align*}d_{\mu}(y_m^*)\geq \sup_{t'\in B(y_m, \delta/2)}d_{\mu}(t')-\frac{1}{k}\geq d_{\mu}(t)-\frac1k, \end{align*} $$
where in the last inequality, we use the fact that
![]() $t\in B(y_m, \delta /2)$
(since
$t\in B(y_m, \delta /2)$
(since
![]() $\rho (y_m, t)\leq \delta /2$
). This proves (3.20), since
$\rho (y_m, t)\leq \delta /2$
). This proves (3.20), since
![]() $y^*_{m}\in B(t,\delta )\cap Y^*$
by (3.21).
$y^*_{m}\in B(t,\delta )\cap Y^*$
by (3.21).
Set for
![]() $n\in {\Bbb N}$
,
$n\in {\Bbb N}$
,
By (3.20),
![]() ${\Omega }=\bigcup _{n=1}^{\infty } {\Omega }_n$
. Define
${\Omega }=\bigcup _{n=1}^{\infty } {\Omega }_n$
. Define
By (3.17), we see that
![]() $A\cap {\Omega }_n\subset E_n$
for each
$A\cap {\Omega }_n\subset E_n$
for each
![]() $n\in {\Bbb N}$
. However, by Proposition 3.1(i) and (3.18), for each
$n\in {\Bbb N}$
. However, by Proposition 3.1(i) and (3.18), for each
![]() $n\in {\Bbb N}$
and
$n\in {\Bbb N}$
and
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in B(y_n^*,\delta )$
,
$t\in B(y_n^*,\delta )$
,
It follows that
![]() $\eta (E_n)=0$
for each
$\eta (E_n)=0$
for each
![]() $n\in {\Bbb N}$
. Hence
$n\in {\Bbb N}$
. Hence
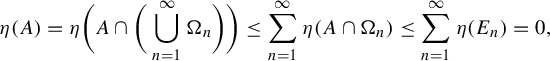 $$ \begin{align*}\eta(A)=\eta\bigg(A\cap \bigg( \bigcup_{n=1}^{\infty} {\Omega}_n\bigg)\bigg)\leq \sum_{n=1}^{\infty} \eta(A\cap {\Omega}_n)\leq \sum_{n=1}^{\infty} \eta(E_n)=0, \end{align*} $$
$$ \begin{align*}\eta(A)=\eta\bigg(A\cap \bigg( \bigcup_{n=1}^{\infty} {\Omega}_n\bigg)\bigg)\leq \sum_{n=1}^{\infty} \eta(A\cap {\Omega}_n)\leq \sum_{n=1}^{\infty} \eta(E_n)=0, \end{align*} $$
leading to a contradiction. This proves the statement that for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in {\Omega }$
,
$t\in {\Omega }$
,
![]() $\Pi ^t_*\mu $
is exact dimensional with dimension
$\Pi ^t_*\mu $
is exact dimensional with dimension
![]() $\min \{d, d_{\mu }(t)\}$
.
$\min \{d, d_{\mu }(t)\}$
.
Next we prove that
![]() $\Pi ^t_*\mu \ll \mathcal L_d$
for
$\Pi ^t_*\mu \ll \mathcal L_d$
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in \{t'\in {\Omega }:\; d_{\mu }(t')>d\}$
. Again we use a contradiction. Suppose on the contrary that this result is false. Then there exist
$t\in \{t'\in {\Omega }:\; d_{\mu }(t')>d\}$
. Again we use a contradiction. Suppose on the contrary that this result is false. Then there exist
![]() $k\in {\Bbb N}$
and
$k\in {\Bbb N}$
and
![]() $A'\subset {\Omega }$
with
$A'\subset {\Omega }$
with
![]() $\eta (A')>0$
such that
$\eta (A')>0$
such that
Set
Clearly,
![]() $A'\cap {\Omega }_n\subset F_n$
for each
$A'\cap {\Omega }_n\subset F_n$
for each
![]() $n\in {\Bbb N}$
. Since
$n\in {\Bbb N}$
. Since
![]() ${\Omega }=\bigcup _{n=1}^{\infty } {\Omega }_n$
and
${\Omega }=\bigcup _{n=1}^{\infty } {\Omega }_n$
and
![]() $\eta (A')>0$
, there exists
$\eta (A')>0$
, there exists
![]() $m\in {\Bbb N}$
so that
$m\in {\Bbb N}$
so that
![]() $\eta (A'\cap {\Omega }_m)>0$
. Hence
$\eta (A'\cap {\Omega }_m)>0$
. Hence
![]() $A'\cap {\Omega }_m\neq \emptyset $
. Pick
$A'\cap {\Omega }_m\neq \emptyset $
. Pick
![]() $t\in A'\cap {\Omega }_m$
. By (3.22), (3.23) and (3.18),
$t\in A'\cap {\Omega }_m$
. By (3.22), (3.23) and (3.18),
Hence
![]() $\eta (F_m)=0$
by Proposition 3.1(ii). Since
$\eta (F_m)=0$
by Proposition 3.1(ii). Since
![]() $A'\cap {\Omega }_m\subset F_m$
, it follows that
$A'\cap {\Omega }_m\subset F_m$
, it follows that
![]() $\eta (A'\cap {\Omega }_m)=0$
, leading to a contradiction.
$\eta (A'\cap {\Omega }_m)=0$
, leading to a contradiction.
Proof of Theorem 1.2(ii) By Lemma 2.6, for each
![]() $t\in {\Omega }$
, we can find a
$t\in {\Omega }$
, we can find a
![]() $\sigma $
-invariant ergodic measure
$\sigma $
-invariant ergodic measure
![]() $\mu _t$
on
$\mu _t$
on
![]() $\Sigma $
such that
$\Sigma $
such that
Moreover,
![]() $0\leq d(t)\leq (\log \ell /\log (1/\theta ))$
.
$0\leq d(t)\leq (\log \ell /\log (1/\theta ))$
.
Next we prove that
![]() $\dim _H K^t=\dim _BK^t=\min \{d, d(t)\}$
for
$\dim _H K^t=\dim _BK^t=\min \{d, d(t)\}$
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in {\Omega }$
. By Theorem 2.7,
$t\in {\Omega }$
. By Theorem 2.7,
![]() $\overline {\dim }_B K^t\leq \min \{d, d(t)\}$
for every
$\overline {\dim }_B K^t\leq \min \{d, d(t)\}$
for every
![]() $t\in {\Omega }$
. Hence it is sufficient to show that
$t\in {\Omega }$
. Hence it is sufficient to show that
Suppose on the contrary that this statement is false. Then there exist
![]() $k\in {\Bbb N}$
and
$k\in {\Bbb N}$
and
![]() $H\subset {\Omega }$
with
$H\subset {\Omega }$
with
![]() $\eta (H)>0$
such that
$\eta (H)>0$
such that
Take a number
![]() $\delta \in (0,\delta _0)$
such that (3.18) holds. Since
$\delta \in (0,\delta _0)$
such that (3.18) holds. Since
![]() $d(t)$
is uniformly bounded from above, similar to the construction of
$d(t)$
is uniformly bounded from above, similar to the construction of
![]() $Y^*$
in the proof of part (i), we can construct a countable dense subset
$Y^*$
in the proof of part (i), we can construct a countable dense subset
![]() $Y'=\{y^{\prime }_n\}_{n=1}^{\infty }$
of
$Y'=\{y^{\prime }_n\}_{n=1}^{\infty }$
of
![]() ${\Omega }$
such that
${\Omega }$
such that
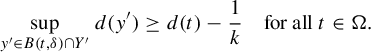 $$ \begin{align} \sup_{y'\in B(t, \delta)\cap Y'} d(y')\geq d(t)-\frac1k \quad \text{for all } t\in {\Omega}. \end{align} $$
$$ \begin{align} \sup_{y'\in B(t, \delta)\cap Y'} d(y')\geq d(t)-\frac1k \quad \text{for all } t\in {\Omega}. \end{align} $$
Write
By (3.25),
![]() ${\Omega }=\bigcup _{n=1}^{\infty } {\Omega }_n'$
. Notice that for each
${\Omega }=\bigcup _{n=1}^{\infty } {\Omega }_n'$
. Notice that for each
![]() $n\in {\Bbb N}$
,
$n\in {\Bbb N}$
,
 $$ \begin{align*} {\Omega}_n'\cap H&\subset \{t\in B(y_n', \delta):\; \dim_H K^t<\min\{d, d(y_n')\}-1/k\}\\ &\subset \{t\in B(y_n', \delta):\; \underline{\dim}_H \Pi^t_*(\mu_{y_n'})<\min\{d, d_{\mu_{y_n'}} (y_n')\}-1/k\}\\ &\subset \bigg\{t\in B(y_n', \delta):\; \underline{\dim}_H \Pi^t_*(\mu_{y_n'})<\min\{d, d_{\mu_{y_n'}} (y_n')\}-\frac{ \psi(\delta)}{\log (1/\theta)}\bigg\}, \end{align*} $$
$$ \begin{align*} {\Omega}_n'\cap H&\subset \{t\in B(y_n', \delta):\; \dim_H K^t<\min\{d, d(y_n')\}-1/k\}\\ &\subset \{t\in B(y_n', \delta):\; \underline{\dim}_H \Pi^t_*(\mu_{y_n'})<\min\{d, d_{\mu_{y_n'}} (y_n')\}-1/k\}\\ &\subset \bigg\{t\in B(y_n', \delta):\; \underline{\dim}_H \Pi^t_*(\mu_{y_n'})<\min\{d, d_{\mu_{y_n'}} (y_n')\}-\frac{ \psi(\delta)}{\log (1/\theta)}\bigg\}, \end{align*} $$
where we have used the facts that
![]() $\dim _H K^t\geq \underline {\dim }_H \Pi ^t_*(\mu _{y_n'})$
and
$\dim _H K^t\geq \underline {\dim }_H \Pi ^t_*(\mu _{y_n'})$
and
![]() $d(y_n')=d_{\mu _{y_n'}} (y_n')$
in the second inclusion, and (3.18) in the last inclusion. Hence
$d(y_n')=d_{\mu _{y_n'}} (y_n')$
in the second inclusion, and (3.18) in the last inclusion. Hence
![]() $\eta ({\Omega }_n'\cap H)=0$
for each n by applying Proposition 3.1(i). It follows that
$\eta ({\Omega }_n'\cap H)=0$
for each n by applying Proposition 3.1(i). It follows that
![]() $\eta (H)\leq \sum _{n=1}^{\infty } \eta ({\Omega }_n'\cap H)=0$
, leading to a contradiction. This completes the proof of the statement that
$\eta (H)\leq \sum _{n=1}^{\infty } \eta ({\Omega }_n'\cap H)=0$
, leading to a contradiction. This completes the proof of the statement that
![]() $\dim _H K^t=\min \{d, d(t)\}$
for
$\dim _H K^t=\min \{d, d(t)\}$
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in {\Omega }$
.
$t\in {\Omega }$
.
Finally, we prove that
![]() $\mathcal L_d(K^t)>0$
for
$\mathcal L_d(K^t)>0$
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in \{t'\in {\Omega }:\; d(t')>d\}$
. Suppose on the contrary that this result is false. Then there exist
$t\in \{t'\in {\Omega }:\; d(t')>d\}$
. Suppose on the contrary that this result is false. Then there exist
![]() $k\in {\Bbb N}$
and
$k\in {\Bbb N}$
and
![]() $H'\subset {\Omega }$
with
$H'\subset {\Omega }$
with
![]() $\eta (H')>0$
such that
$\eta (H')>0$
such that
Set
Clearly,
![]() $H'\cap {\Omega }_n'\subset F^{\prime }_n$
for each
$H'\cap {\Omega }_n'\subset F^{\prime }_n$
for each
![]() $n\in {\Bbb N}$
. Since
$n\in {\Bbb N}$
. Since
![]() ${\Omega }=\bigcup _{n=1}^{\infty } {\Omega }_n'$
and
${\Omega }=\bigcup _{n=1}^{\infty } {\Omega }_n'$
and
![]() $\eta (H')>0$
, there exists
$\eta (H')>0$
, there exists
![]() $m\in {\Bbb N}$
so that
$m\in {\Bbb N}$
so that
![]() $\eta (H'\cap {\Omega }_m')>0$
. Hence
$\eta (H'\cap {\Omega }_m')>0$
. Hence
![]() $H'\cap {\Omega }_m'\neq \emptyset $
. Taking
$H'\cap {\Omega }_m'\neq \emptyset $
. Taking
![]() $t\in H'\cap {\Omega }_m'$
and applying (3.26), (3.27) and (3.18) gives
$t\in H'\cap {\Omega }_m'$
and applying (3.26), (3.27) and (3.18) gives
Now by Proposition 3.1(ii),
![]() $\Pi ^t_*(\mu _{y_m'})\ll \mathcal L_d$
for
$\Pi ^t_*(\mu _{y_m'})\ll \mathcal L_d$
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $t\in B(y_m', \delta )$
. This implies that
$t\in B(y_m', \delta )$
. This implies that
![]() $\eta (F_m')=0$
. Since
$\eta (F_m')=0$
. Since
![]() $H'\cap {\Omega }_m'\subset F_m'$
, it follows that
$H'\cap {\Omega }_m'\subset F_m'$
, it follows that
![]() $\eta (H'\cap {\Omega }_m')=0$
, leading to a contradiction.
$\eta (H'\cap {\Omega }_m')=0$
, leading to a contradiction.
4 Translational family of IFSs generated by a dominated lower triangular
 $C^1$
IFS
$C^1$
IFS
In this section, we show that under mild assumptions, a translational family of
![]() $C^1$
IFSs, generated by a dominated lower triangular
$C^1$
IFSs, generated by a dominated lower triangular
![]() $C^1$
IFS, satisfies the GTC. To begin with, let S be a compact subset of
$C^1$
IFS, satisfies the GTC. To begin with, let S be a compact subset of
![]() ${\Bbb R}^d$
with non-empty interior.
${\Bbb R}^d$
with non-empty interior.
Definition 4.1. Let
![]() $\ell \in {\Bbb N}$
with
$\ell \in {\Bbb N}$
with
![]() $\ell \geq 2$
. We say that
$\ell \geq 2$
. We say that
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
is a dominated lower triangular
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
is a dominated lower triangular
![]() $C^1$
IFS on S if the following conditions hold.
$C^1$
IFS on S if the following conditions hold.
-
(i)
 $f_i(S)\subset \mathrm {int} (S)$
,
$f_i(S)\subset \mathrm {int} (S)$
,
 $i=1,\ldots , \ell $
.
$i=1,\ldots , \ell $
. -
(ii) There exists a bounded open connected set
 $U\supset S$
such that each
$U\supset S$
such that each
 $f_i$
extends to a contracting
$f_i$
extends to a contracting
 $C^1$
diffeomorphism
$C^1$
diffeomorphism
 $f_i: U\to f_i(U)$
with
$f_i: U\to f_i(U)$
with
 $\overline {f_i(U)}\subset U$
.
$\overline {f_i(U)}\subset U$
. -
(iii) For each
 $z\in S$
and
$z\in S$
and
 $i\in \{1,\ldots , \ell \}$
, the Jacobian matrix
$i\in \{1,\ldots , \ell \}$
, the Jacobian matrix
 $D_zf_i$
of
$D_zf_i$
of
 $f_i$
at z is a lower triangular matrix such that
$f_i$
at z is a lower triangular matrix such that  $$ \begin{align*}|(D_zf_i)_{\mathit{jj}}|\leq |(D_zf_i)_{kk}|\quad \text{for all }1\leq k\leq j\leq d. \end{align*} $$
$$ \begin{align*}|(D_zf_i)_{\mathit{jj}}|\leq |(D_zf_i)_{kk}|\quad \text{for all }1\leq k\leq j\leq d. \end{align*} $$
In the remaining part of this section, we fix a dominated lower triangular
![]() $C^1$
IFS
$C^1$
IFS
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
on S.
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
on S.
By continuity, there exists a small
![]() $r_0>0$
such that the following holds. Setting
$r_0>0$
such that the following holds. Setting
for
![]() $1\leq i\leq \ell $
and
$1\leq i\leq \ell $
and
![]() $\boldsymbol {\mathfrak {t}}=(\mathbf {t}_1,\ldots , \mathbf {t}_{\ell })\in {\Bbb R}^{\ell d}$
with
$\boldsymbol {\mathfrak {t}}=(\mathbf {t}_1,\ldots , \mathbf {t}_{\ell })\in {\Bbb R}^{\ell d}$
with
![]() $|\boldsymbol {\mathfrak {t}}|< r_0$
, we have
$|\boldsymbol {\mathfrak {t}}|< r_0$
, we have
![]() $f_i^{\boldsymbol {\mathfrak {t}}}(S)\subset \mathrm {int}(S)$
for each i.
$f_i^{\boldsymbol {\mathfrak {t}}}(S)\subset \mathrm {int}(S)$
for each i.
Write
![]() $\Delta :=\{\boldsymbol {\mathfrak {t}}\in {\Bbb R}^{\ell d}:\; |\boldsymbol {\mathfrak {t}}|<r_0\}$
and set
$\Delta :=\{\boldsymbol {\mathfrak {t}}\in {\Bbb R}^{\ell d}:\; |\boldsymbol {\mathfrak {t}}|<r_0\}$
and set
We call
![]() $\mathcal F^{\boldsymbol {\mathfrak {t}}}$
,
$\mathcal F^{\boldsymbol {\mathfrak {t}}}$
,
![]() ${\boldsymbol {\mathfrak {t}}\in \Delta }$
, a translational family of IFSs generated by
${\boldsymbol {\mathfrak {t}}\in \Delta }$
, a translational family of IFSs generated by
![]() $\mathcal F$
. For
$\mathcal F$
. For
![]() $\mathbf {i}=i_1\ldots i_n\in \Sigma _n$
, we write
$\mathbf {i}=i_1\ldots i_n\in \Sigma _n$
, we write
![]() $f_{\mathbf { i}}^{\boldsymbol {\mathfrak {t}}}=f_{i_1}^{\boldsymbol {\mathfrak {t}}}\circ \cdots \circ f_{i_n}^{\boldsymbol {\mathfrak {t}}}$
.
$f_{\mathbf { i}}^{\boldsymbol {\mathfrak {t}}}=f_{i_1}^{\boldsymbol {\mathfrak {t}}}\circ \cdots \circ f_{i_n}^{\boldsymbol {\mathfrak {t}}}$
.
For a
![]() $C^1$
map
$C^1$
map
![]() $g: S\to {\Bbb R}^d$
and
$g: S\to {\Bbb R}^d$
and
![]() $z_1,\ldots , z_d\in S$
, we write
$z_1,\ldots , z_d\in S$
, we write
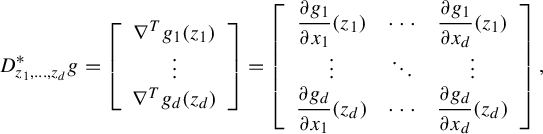 $$ \begin{align} D_{z_1,\ldots, z_d}^*g=\left[\begin{array}{c} \nabla^Tg_1(z_1) \\ \vdots \\ \nabla^Tg_d(z_d) \end{array}\right]=\left[ \begin{array}{ccc} \displaystyle\frac{\partial g_1}{\partial x_1}(z_1) & \cdots &\displaystyle\frac{\partial g_1}{\partial x_d}(z_1)\\ \vdots & \ddots & \vdots \\ \displaystyle\frac{\partial g_d}{\partial x_1}(z_d) & \cdots &\displaystyle\frac{\partial g_d}{\partial x_d}(z_d) \end{array} \right], \end{align} $$
$$ \begin{align} D_{z_1,\ldots, z_d}^*g=\left[\begin{array}{c} \nabla^Tg_1(z_1) \\ \vdots \\ \nabla^Tg_d(z_d) \end{array}\right]=\left[ \begin{array}{ccc} \displaystyle\frac{\partial g_1}{\partial x_1}(z_1) & \cdots &\displaystyle\frac{\partial g_1}{\partial x_d}(z_1)\\ \vdots & \ddots & \vdots \\ \displaystyle\frac{\partial g_d}{\partial x_1}(z_d) & \cdots &\displaystyle\frac{\partial g_d}{\partial x_d}(z_d) \end{array} \right], \end{align} $$
where
![]() $g_i$
is the ith component of the map g,
$g_i$
is the ith component of the map g,
![]() $i=1,\ldots , d$
. Clearly,
$i=1,\ldots , d$
. Clearly,
The main result in this section is the following.
Theorem 4.2. Let
![]() $\mathcal F^{\boldsymbol {\mathfrak {t}}}$
,
$\mathcal F^{\boldsymbol {\mathfrak {t}}}$
,
![]() ${\boldsymbol {\mathfrak {t}}\in \Delta }$
, be a translational family of IFSs generated by a dominated lower triangular
${\boldsymbol {\mathfrak {t}}\in \Delta }$
, be a translational family of IFSs generated by a dominated lower triangular
![]() $C^1$
IFS
$C^1$
IFS
![]() $\mathcal F$
defined on a compact convex subset S of
$\mathcal F$
defined on a compact convex subset S of
![]() ${\Bbb R}^d$
. Suppose in addition that
${\Bbb R}^d$
. Suppose in addition that
Then
![]() $\mathcal F^{\boldsymbol {\mathfrak {t}}}$
,
$\mathcal F^{\boldsymbol {\mathfrak {t}}}$
,
![]() $\boldsymbol {\mathfrak {t}}\in \Delta $
, satisfies the GTC with respect to
$\boldsymbol {\mathfrak {t}}\in \Delta $
, satisfies the GTC with respect to
![]() $\ell d$
-dimensional Lebesgue measure
$\ell d$
-dimensional Lebesgue measure
![]() $\mathcal L_{\ell d}$
restricted to
$\mathcal L_{\ell d}$
restricted to
![]() $\Delta $
.
$\Delta $
.
The proof of the above theorem is based on the following.
Proposition 4.3. Let
![]() $\mathcal F^{\boldsymbol {\mathfrak {t}}}$
,
$\mathcal F^{\boldsymbol {\mathfrak {t}}}$
,
![]() ${\boldsymbol {\mathfrak {t}}\in \Delta }$
, be a translational family of IFSs generated by a dominated lower triangular
${\boldsymbol {\mathfrak {t}}\in \Delta }$
, be a translational family of IFSs generated by a dominated lower triangular
![]() $C^1$
IFS
$C^1$
IFS
![]() $\mathcal F$
on a compact subset S of
$\mathcal F$
on a compact subset S of
![]() ${\Bbb R}^d$
. Then there exists a function
${\Bbb R}^d$
. Then there exists a function
![]() $h: (0, r_0)\to (0,\infty )$
with
$h: (0, r_0)\to (0,\infty )$
with
![]() $\lim _{\delta \to 0} h(\delta )=0$
such that for each
$\lim _{\delta \to 0} h(\delta )=0$
such that for each
![]() $\delta \in (0,r_0)$
, there is
$\delta \in (0,r_0)$
, there is
![]() $C(\delta )\geq 1$
so that
$C(\delta )\geq 1$
so that
for every
![]() $n\in {\Bbb N}$
,
$n\in {\Bbb N}$
,
![]() $\boldsymbol {\omega }\in \Sigma _n$
,
$\boldsymbol {\omega }\in \Sigma _n$
,
![]() $y, z_1,\ldots , z_d\in S$
and
$y, z_1,\ldots , z_d\in S$
and
![]() $\boldsymbol {\mathfrak {s}},\boldsymbol {\mathfrak {t}}\in \Delta $
with
$\boldsymbol {\mathfrak {s}},\boldsymbol {\mathfrak {t}}\in \Delta $
with
![]() $|\boldsymbol {\mathfrak {s}}-\boldsymbol {\mathfrak {t}}|<\delta $
.
$|\boldsymbol {\mathfrak {s}}-\boldsymbol {\mathfrak {t}}|<\delta $
.
In the next two subsections, we prove Proposition 4.3 and Theorem 4.2, respectively.
4.1 Proof of Proposition 4.3
We first prove several auxiliary lemmas.
Lemma 4.4. Let
![]() $c\geq 1$
and
$c\geq 1$
and
![]() $d\in {\Bbb N}$
. Let A be a real
$d\in {\Bbb N}$
. Let A be a real
![]() $d\times d$
non-singular lower triangular matrix such that
$d\times d$
non-singular lower triangular matrix such that
Then
Proof It is well known (see e.g. [Reference Horn and Johnson28]) that
![]() $A^{-1}=({1}/{\det (A)}) \text {adj}(A)$
, where
$A^{-1}=({1}/{\det (A)}) \text {adj}(A)$
, where
![]() $\text {adj}(A)$
is the adjugate matrix of A defined by
$\text {adj}(A)$
is the adjugate matrix of A defined by
where
![]() $A(j,i)$
is the
$A(j,i)$
is the
![]() $(d-1)\times (d-1)$
matrix that results from A by removing the jth row and ith column. By the Hadamard’s inequality (see e.g. [Reference Horn and Johnson28, Corollary 7.8.2]),
$(d-1)\times (d-1)$
matrix that results from A by removing the jth row and ith column. By the Hadamard’s inequality (see e.g. [Reference Horn and Johnson28, Corollary 7.8.2]),
![]() $|\!\det (A(j,i))|$
is bounded above by the product of the Euclidean norms of the columns of
$|\!\det (A(j,i))|$
is bounded above by the product of the Euclidean norms of the columns of
![]() $A(j,i)$
. In particular, this implies that
$A(j,i)$
. In particular, this implies that
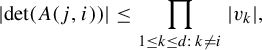 $$ \begin{align*}|\!\det(A(j,i))|\leq \prod_{1\leq k\leq d:\; k\neq i}|v_k|, \end{align*} $$
$$ \begin{align*}|\!\det(A(j,i))|\leq \prod_{1\leq k\leq d:\; k\neq i}|v_k|, \end{align*} $$
where
![]() $v_k$
denotes the kth column vector of A. By (4.5),
$v_k$
denotes the kth column vector of A. By (4.5),
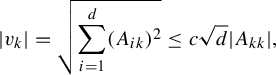 $$ \begin{align*}|v_k|=\sqrt{\sum_{i=1}^d(A_{ik})^2}\leq c\sqrt{d}|A_{kk}|,\end{align*} $$
$$ \begin{align*}|v_k|=\sqrt{\sum_{i=1}^d(A_{ik})^2}\leq c\sqrt{d}|A_{kk}|,\end{align*} $$
so
![]() $|\!\det (A(j,i))|\leq (c\sqrt {d})^{d-1} \prod _{1\leq k\leq d:\; k\neq i} |A_{kk}|$
. Hence for given
$|\!\det (A(j,i))|\leq (c\sqrt {d})^{d-1} \prod _{1\leq k\leq d:\; k\neq i} |A_{kk}|$
. Hence for given
![]() $1\leq i,j\leq d$
,
$1\leq i,j\leq d$
,
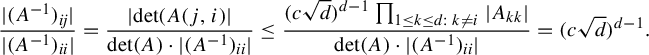 $$ \begin{align*}\frac{|(A^{-1})_{\mathit{ij}}|}{|(A^{-1})_{\mathit{ii}}|}=\frac{|\!\det(A(j,i)|}{\det(A)\cdot |(A^{-1})_{\mathit{ii}}|}\leq \frac{(c\sqrt{d})^{d-1} \prod_{1\leq k\leq d:\; k\neq i} |A_{kk}|}{\det(A)\cdot |(A^{-1})_{\mathit{ii}}|}=(c\sqrt{d})^{d-1}.\\[-42pt] \end{align*} $$
$$ \begin{align*}\frac{|(A^{-1})_{\mathit{ij}}|}{|(A^{-1})_{\mathit{ii}}|}=\frac{|\!\det(A(j,i)|}{\det(A)\cdot |(A^{-1})_{\mathit{ii}}|}\leq \frac{(c\sqrt{d})^{d-1} \prod_{1\leq k\leq d:\; k\neq i} |A_{kk}|}{\det(A)\cdot |(A^{-1})_{\mathit{ii}}|}=(c\sqrt{d})^{d-1}.\\[-42pt] \end{align*} $$
For
![]() $c\geq 1$
and
$c\geq 1$
and
![]() $d\in {\Bbb N}$
, let
$d\in {\Bbb N}$
, let
![]() $\mathcal T_c(d)$
denote the collection of real
$\mathcal T_c(d)$
denote the collection of real
![]() $d\times d$
lower triangular matrices
$d\times d$
lower triangular matrices
![]() $A=(a_{\mathit {ij}})$
satisfying the following two conditions:
$A=(a_{\mathit {ij}})$
satisfying the following two conditions:
-
(i)
 $|a_{11}|\geq |a_{22}|\geq \cdots \geq |a_{dd}|>0$
;
$|a_{11}|\geq |a_{22}|\geq \cdots \geq |a_{dd}|>0$
; -
(ii)
 $|a_{\mathit {ij}}|\leq c|a_{\mathit {jj}}|$
for all
$|a_{\mathit {ij}}|\leq c|a_{\mathit {jj}}|$
for all
 $ 1\leq i,j\leq d$
.
$ 1\leq i,j\leq d$
.
Then we have the following estimates.
Lemma 4.5. Let
![]() $n\in {\Bbb N}$
and
$n\in {\Bbb N}$
and
![]() $A_1,\ldots , A_n\in \mathcal T_c(d)$
. Then for
$A_1,\ldots , A_n\in \mathcal T_c(d)$
. Then for
![]() $1\leq j\leq i\leq d$
,
$1\leq j\leq i\leq d$
,
Proof We prove by induction on n. Since
![]() $A_1\in \mathcal T_c(d)$
, the inequality (4.6) holds when
$A_1\in \mathcal T_c(d)$
, the inequality (4.6) holds when
![]() $n=1$
. Now assume that (4.6) holds when
$n=1$
. Now assume that (4.6) holds when
![]() $n=k$
. Below we show that it also holds when
$n=k$
. Below we show that it also holds when
![]() $n=k+1$
.
$n=k+1$
.
Given
![]() $A_1,\ldots , A_{k+1}\in \mathcal T_c(d)$
, we write
$A_1,\ldots , A_{k+1}\in \mathcal T_c(d)$
, we write
![]() $A=A_1$
and
$A=A_1$
and
![]() $B=A_2\cdots A_{k+1}$
. Clearly B is lower triangular. By the induction assumption,
$B=A_2\cdots A_{k+1}$
. Clearly B is lower triangular. By the induction assumption,
![]() $|B_{\mathit {ij}}|\leq (ck)^{i-j} |B_{\mathit {jj}}|$
for each pair
$|B_{\mathit {ij}}|\leq (ck)^{i-j} |B_{\mathit {jj}}|$
for each pair
![]() $(i,j)$
with
$(i,j)$
with
![]() $1\leq j\leq i\leq d$
.
$1\leq j\leq i\leq d$
.
Now fix a pair
![]() $(i,j)$
with
$(i,j)$
with
![]() $1\leq j\leq i\leq d$
. Observe that
$1\leq j\leq i\leq d$
. Observe that
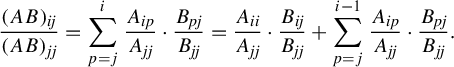 $$ \begin{align} \frac{(AB)_{\mathit{ij}}}{(AB)_{\mathit{jj}}}=\sum_{ p=j}^i\frac{A_{\mathit{ip}}}{A_{\mathit{\mathit{jj}}}} \cdot \frac{B_{\mathit{pj}}}{B_{\mathit{jj}}}=\frac{A_{\mathit{ii}}}{A_{\mathit{jj}}} \cdot \frac{B_{\mathit{ij}}}{B_{\mathit{jj}}}+\sum_{p=j}^{i-1} \frac{A_{\mathit{ip}}}{A_{\mathit{jj}}} \cdot \frac{B_{\mathit{pj}}}{B_{\mathit{jj}}}. \end{align} $$
$$ \begin{align} \frac{(AB)_{\mathit{ij}}}{(AB)_{\mathit{jj}}}=\sum_{ p=j}^i\frac{A_{\mathit{ip}}}{A_{\mathit{\mathit{jj}}}} \cdot \frac{B_{\mathit{pj}}}{B_{\mathit{jj}}}=\frac{A_{\mathit{ii}}}{A_{\mathit{jj}}} \cdot \frac{B_{\mathit{ij}}}{B_{\mathit{jj}}}+\sum_{p=j}^{i-1} \frac{A_{\mathit{ip}}}{A_{\mathit{jj}}} \cdot \frac{B_{\mathit{pj}}}{B_{\mathit{jj}}}. \end{align} $$
Applying the inequalities
![]() $|A_{\mathit {ii}}|\leq |A_{\mathit {jj}}|$
,
$|A_{\mathit {ii}}|\leq |A_{\mathit {jj}}|$
,
![]() $|B_{\mathit {ij}}|\leq (ck)^{i-j}|B_{\mathit {jj}}|$
,
$|B_{\mathit {ij}}|\leq (ck)^{i-j}|B_{\mathit {jj}}|$
,
![]() $|A_{\mathit {ip}}|\leq c|A_{pp}|\leq c|A_{\mathit {jj}}|$
and
$|A_{\mathit {ip}}|\leq c|A_{pp}|\leq c|A_{\mathit {jj}}|$
and
![]() $|B_{\mathit {pj}}|\leq (ck)^{p-j}|B_{\mathit {jj}}|$
to (4.7) gives
$|B_{\mathit {pj}}|\leq (ck)^{p-j}|B_{\mathit {jj}}|$
to (4.7) gives
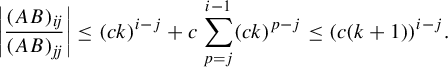 $$ \begin{align*}\bigg|\frac{(AB)_{\mathit{ij}}}{(AB)_{\mathit{jj}}}\bigg|\leq (ck)^{i-j} + c\sum_{p=j}^{i-1}(ck)^{p-j}\leq (c(k+1))^{i-j}. \end{align*} $$
$$ \begin{align*}\bigg|\frac{(AB)_{\mathit{ij}}}{(AB)_{\mathit{jj}}}\bigg|\leq (ck)^{i-j} + c\sum_{p=j}^{i-1}(ck)^{p-j}\leq (c(k+1))^{i-j}. \end{align*} $$
Hence (4.6) holds for
![]() $n=k+1$
.
$n=k+1$
.
Lemma 4.6. Let
![]() $\mathcal F^{\boldsymbol {\mathfrak {t}}}=\{f_i^{\boldsymbol {\mathfrak {t}}}\}_{i=1}^{\ell }$
,
$\mathcal F^{\boldsymbol {\mathfrak {t}}}=\{f_i^{\boldsymbol {\mathfrak {t}}}\}_{i=1}^{\ell }$
,
![]() ${\boldsymbol {\mathfrak {t}}\in \Delta }$
, be a translational family of IFSs on a compact subset S of
${\boldsymbol {\mathfrak {t}}\in \Delta }$
, be a translational family of IFSs on a compact subset S of
![]() ${\Bbb R}^d$
generated by a
${\Bbb R}^d$
generated by a
![]() $C^1$
IFS
$C^1$
IFS
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
. Let
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
. Let
![]() $\theta \in (0,1)$
be a common Lipschitz constant of
$\theta \in (0,1)$
be a common Lipschitz constant of
![]() $f_1,\ldots , f_{\ell }$
on S. That is,
$f_1,\ldots , f_{\ell }$
on S. That is,
Then for
![]() ${\mathfrak {s}}, {\mathfrak {t}}\in \Delta $
,
${\mathfrak {s}}, {\mathfrak {t}}\in \Delta $
,
![]() $u,v\in S$
,
$u,v\in S$
,
![]() $n\in {\Bbb N}$
and
$n\in {\Bbb N}$
and
![]() $\boldsymbol {\tau }\in \Sigma _{n}$
,
$\boldsymbol {\tau }\in \Sigma _{n}$
,
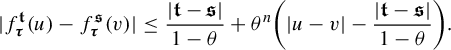 $$ \begin{align} | f^{\boldsymbol{\mathfrak{t}} }_{\boldsymbol{\tau}}(u) - f^{\boldsymbol{\mathfrak{s}} }_{\boldsymbol{\tau}}(v) | \leq \frac{|\boldsymbol{\mathfrak{t}} -\boldsymbol{\mathfrak{s}}|}{1-\theta} + \theta^{n} \bigg( |u-v|- \frac{|\boldsymbol{\mathfrak{t}} -\boldsymbol{\mathfrak{s}}|}{1-\theta} \bigg). \end{align} $$
$$ \begin{align} | f^{\boldsymbol{\mathfrak{t}} }_{\boldsymbol{\tau}}(u) - f^{\boldsymbol{\mathfrak{s}} }_{\boldsymbol{\tau}}(v) | \leq \frac{|\boldsymbol{\mathfrak{t}} -\boldsymbol{\mathfrak{s}}|}{1-\theta} + \theta^{n} \bigg( |u-v|- \frac{|\boldsymbol{\mathfrak{t}} -\boldsymbol{\mathfrak{s}}|}{1-\theta} \bigg). \end{align} $$
In particular,
Proof To verify (4.8), we let
![]() $i\in \{1,\ldots , \ell \}$
. Then
$i\in \{1,\ldots , \ell \}$
. Then
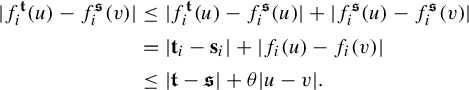 $$ \begin{align*} | f^{\boldsymbol{\mathfrak{t}} }_i(u)-f^{\boldsymbol{\mathfrak{s}}}_i(v) | &\leq | f^{\boldsymbol{\mathfrak{t}} }_i(u)-f^{\boldsymbol{\mathfrak{s}} }_i(u) | + | f^{\boldsymbol{\mathfrak{s}} }_i(u)-f^{\boldsymbol{\mathfrak{s}} }_i(v) | \\ &= | \mathbf{t}_i-\mathbf{s}_i | + | f_i(u)-f_i(v) | \\ &\leq | \boldsymbol{\mathfrak{t}}-\boldsymbol{\mathfrak{s}} | +\theta|u-v|. \end{align*} $$
$$ \begin{align*} | f^{\boldsymbol{\mathfrak{t}} }_i(u)-f^{\boldsymbol{\mathfrak{s}}}_i(v) | &\leq | f^{\boldsymbol{\mathfrak{t}} }_i(u)-f^{\boldsymbol{\mathfrak{s}} }_i(u) | + | f^{\boldsymbol{\mathfrak{s}} }_i(u)-f^{\boldsymbol{\mathfrak{s}} }_i(v) | \\ &= | \mathbf{t}_i-\mathbf{s}_i | + | f_i(u)-f_i(v) | \\ &\leq | \boldsymbol{\mathfrak{t}}-\boldsymbol{\mathfrak{s}} | +\theta|u-v|. \end{align*} $$
Let
![]() $\varphi :\;{\Bbb R}\to {\Bbb R}$
be a contracting affine map defined by
$\varphi :\;{\Bbb R}\to {\Bbb R}$
be a contracting affine map defined by
![]() $\varphi (x)= | \boldsymbol {\mathfrak {t}}-\boldsymbol {\mathfrak {s}} | +\theta x$
for given
$\varphi (x)= | \boldsymbol {\mathfrak {t}}-\boldsymbol {\mathfrak {s}} | +\theta x$
for given
![]() $\boldsymbol {\mathfrak {s}}$
and
$\boldsymbol {\mathfrak {s}}$
and
![]() $\boldsymbol {\mathfrak {t}}$
. Then for every
$\boldsymbol {\mathfrak {t}}$
. Then for every
![]() $1\leq i\leq \ell $
,
$1\leq i\leq \ell $
,
Now we can prove (4.8) by using the above inequality. Indeed, using (4.10) and the fact that
![]() $\varphi (\cdot )$
is monotone increasing, we obtain that for
$\varphi (\cdot )$
is monotone increasing, we obtain that for
![]() $1\leq i,j\leq \ell $
,
$1\leq i,j\leq \ell $
,
Successive application of this implies that for every
![]() $\boldsymbol {\tau }\in \Sigma _{n}$
and
$\boldsymbol {\tau }\in \Sigma _{n}$
and
![]() $u,v\in S$
,
$u,v\in S$
,
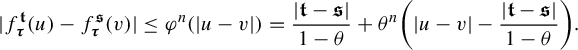 $$ \begin{align*}| f^{\boldsymbol{\mathfrak{t}} }_{\boldsymbol{\tau}}(u) - f^{\boldsymbol{\mathfrak{s}} }_{\boldsymbol{\tau}}(v) | \leq \varphi^{n}(|u-v|)=\frac{|\boldsymbol{\mathfrak{t}} -\boldsymbol{\mathfrak{s}}|}{1-\theta} + \theta^{n} \bigg( |u-v|- \frac{|\boldsymbol{\mathfrak{t}} -\boldsymbol{\mathfrak{s}}|}{1-\theta} \bigg). \end{align*} $$
$$ \begin{align*}| f^{\boldsymbol{\mathfrak{t}} }_{\boldsymbol{\tau}}(u) - f^{\boldsymbol{\mathfrak{s}} }_{\boldsymbol{\tau}}(v) | \leq \varphi^{n}(|u-v|)=\frac{|\boldsymbol{\mathfrak{t}} -\boldsymbol{\mathfrak{s}}|}{1-\theta} + \theta^{n} \bigg( |u-v|- \frac{|\boldsymbol{\mathfrak{t}} -\boldsymbol{\mathfrak{s}}|}{1-\theta} \bigg). \end{align*} $$
This proves (4.8). The assertions in (4.9) then follow directly from (4.8).
Now we are ready to prove Proposition 4.3.
Proof of Proposition 4.3 We divide the proof into five small steps.
Step 1. Write
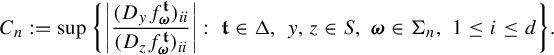 $$ \begin{align} C_n:=\sup\bigg\{ \bigg|\frac{(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}{(D_zf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}\bigg|:\; \boldsymbol{\mathfrak{t}}\in \Delta,\; y,z\in S, \;{\boldsymbol{\omega}}\in \Sigma_n,\; 1\leq i\leq d\bigg\}. \end{align} $$
$$ \begin{align} C_n:=\sup\bigg\{ \bigg|\frac{(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}{(D_zf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}\bigg|:\; \boldsymbol{\mathfrak{t}}\in \Delta,\; y,z\in S, \;{\boldsymbol{\omega}}\in \Sigma_n,\; 1\leq i\leq d\bigg\}. \end{align} $$
We claim that
To prove this claim, for each
![]() $p\in \{1,\ldots , \ell \}$
and
$p\in \{1,\ldots , \ell \}$
and
![]() $i\in \{1,\ldots , d\}$
, we define a function
$i\in \{1,\ldots , d\}$
, we define a function
![]() $a_{p,i}:\; S\to {\Bbb R}$
by
$a_{p,i}:\; S\to {\Bbb R}$
by
Clearly, the functions
![]() $a_{p,i}$
are continuous on S. Since the matrix
$a_{p,i}$
are continuous on S. Since the matrix
![]() $D_zf_p$
is lower triangular for each
$D_zf_p$
is lower triangular for each
![]() $z\in S$
and
$z\in S$
and
![]() $1\leq p\leq \ell $
, it follows that for
$1\leq p\leq \ell $
, it follows that for
![]() $\boldsymbol {\mathfrak {t}}\in \Delta $
,
$\boldsymbol {\mathfrak {t}}\in \Delta $
,
![]() $y,z\in S$
,
$y,z\in S$
,
![]() ${\boldsymbol {\omega }}=\omega _1\cdots \omega _n\in \Sigma _n$
and
${\boldsymbol {\omega }}=\omega _1\cdots \omega _n\in \Sigma _n$
and
![]() $1\leq i\leq d$
,
$1\leq i\leq d$
,
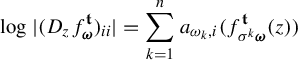 $$ \begin{align} \log |(D_zf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}|=\sum_{k=1}^n a_{\omega_k,i}(f^{\boldsymbol{\mathfrak{t}}}_{\sigma^k{{\boldsymbol{\omega}}}}(z)) \end{align} $$
$$ \begin{align} \log |(D_zf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}|=\sum_{k=1}^n a_{\omega_k,i}(f^{\boldsymbol{\mathfrak{t}}}_{\sigma^k{{\boldsymbol{\omega}}}}(z)) \end{align} $$
and
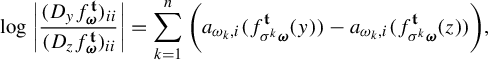 $$ \begin{align} \log \bigg|\frac{(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}{(D_zf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}\bigg|=\sum_{k=1}^n \bigg(a_{\omega_k,i}(f^{\boldsymbol{\mathfrak{t}}}_{\sigma^k{{\boldsymbol{\omega}}}}(y))- a_{\omega_k,i}(f^{\boldsymbol{\mathfrak{t}}}_{\sigma^k{{\boldsymbol{\omega}}}}(z))\bigg), \end{align} $$
$$ \begin{align} \log \bigg|\frac{(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}{(D_zf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}\bigg|=\sum_{k=1}^n \bigg(a_{\omega_k,i}(f^{\boldsymbol{\mathfrak{t}}}_{\sigma^k{{\boldsymbol{\omega}}}}(y))- a_{\omega_k,i}(f^{\boldsymbol{\mathfrak{t}}}_{\sigma^k{{\boldsymbol{\omega}}}}(z))\bigg), \end{align} $$
where
![]() $\sigma ^k{{\boldsymbol {\omega }}}:=\omega _{k+1}\cdots \omega _n$
for
$\sigma ^k{{\boldsymbol {\omega }}}:=\omega _{k+1}\cdots \omega _n$
for
![]() $1\leq k\leq n-1$
,
$1\leq k\leq n-1$
,
![]() $\sigma ^n{{\boldsymbol {\omega }}}:=\varepsilon $
(here
$\sigma ^n{{\boldsymbol {\omega }}}:=\varepsilon $
(here
![]() $\varepsilon $
stands for the empty word) and
$\varepsilon $
stands for the empty word) and
![]() $f^{\boldsymbol {\mathfrak {t}}}_{\varepsilon }(y):=y$
. Define
$f^{\boldsymbol {\mathfrak {t}}}_{\varepsilon }(y):=y$
. Define
![]() $\gamma : (0,\infty )\to (0,\infty )$
by
$\gamma : (0,\infty )\to (0,\infty )$
by
Since S is compact and
![]() $a_{p,i}$
are continuous, it follows that
$a_{p,i}$
are continuous, it follows that
![]() $\lim _{u\to 0}\gamma (u)=0$
. To estimate the term in the left-hand side of the equality (4.14), by Lemma 4.6 we obtain that
$\lim _{u\to 0}\gamma (u)=0$
. To estimate the term in the left-hand side of the equality (4.14), by Lemma 4.6 we obtain that
where
![]() $\theta \in (0,1)$
is a common Lipschitz constant of
$\theta \in (0,1)$
is a common Lipschitz constant of
![]() $f_1,\ldots , f_{\ell }$
on S. Hence by (4.14),
$f_1,\ldots , f_{\ell }$
on S. Hence by (4.14),
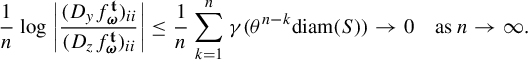 $$ \begin{align*}\frac{1}{n} \log \bigg|\frac{(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}{(D_zf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}\bigg|\leq \frac{1}{n} \sum_{k=1}^n\gamma(\theta^{n-k}\mathrm{diam}(S))\to 0\quad \text{as }n\to \infty. \end{align*} $$
$$ \begin{align*}\frac{1}{n} \log \bigg|\frac{(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}{(D_zf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}\bigg|\leq \frac{1}{n} \sum_{k=1}^n\gamma(\theta^{n-k}\mathrm{diam}(S))\to 0\quad \text{as }n\to \infty. \end{align*} $$
This proves (4.12).
Step 2. For
![]() $\boldsymbol {\mathfrak {s}},\boldsymbol {\mathfrak {t}}\in \Delta $
,
$\boldsymbol {\mathfrak {s}},\boldsymbol {\mathfrak {t}}\in \Delta $
,
![]() $y\in S$
,
$y\in S$
,
![]() $n\in {\Bbb N}$
,
$n\in {\Bbb N}$
,
![]() ${\boldsymbol {\omega }}\in \Sigma _n$
and
${\boldsymbol {\omega }}\in \Sigma _n$
and
![]() $1\leq i\leq d$
,
$1\leq i\leq d$
,
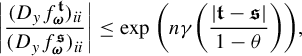 $$ \begin{align} \bigg|\frac{(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}{(D_yf^{\boldsymbol{\mathfrak{s}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}\bigg|\leq \exp\bigg(n\gamma\bigg(\frac{|\boldsymbol{\mathfrak{t}}-\boldsymbol{\mathfrak{s}}|}{1-\theta}\bigg)\bigg), \end{align} $$
$$ \begin{align} \bigg|\frac{(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}{(D_yf^{\boldsymbol{\mathfrak{s}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}\bigg|\leq \exp\bigg(n\gamma\bigg(\frac{|\boldsymbol{\mathfrak{t}}-\boldsymbol{\mathfrak{s}}|}{1-\theta}\bigg)\bigg), \end{align} $$
where
![]() $\gamma (\cdot )$
is defined as in (4.15) and
$\gamma (\cdot )$
is defined as in (4.15) and
![]() $\theta \in (0,1)$
is a common Lipschitz constant for
$\theta \in (0,1)$
is a common Lipschitz constant for
![]() $f_1,\ldots , f_{\ell }$
on S.
$f_1,\ldots , f_{\ell }$
on S.
To prove (4.16), by (4.13) we see that
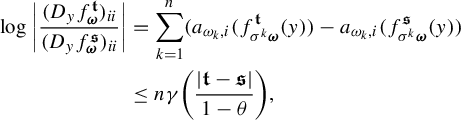 $$ \begin{align*} \log \bigg|\frac{(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}{(D_yf^{\boldsymbol{\mathfrak{s}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}\bigg|&=\sum_{k=1}^n (a_{\omega_k,i}(f^{\boldsymbol{\mathfrak{t}}}_{\sigma^k{{\boldsymbol{\omega}}}}(y))- a_{\omega_k,i}(f^{\boldsymbol{\mathfrak{s}}}_{\sigma^k{{\boldsymbol{\omega}}}}(y))\\ &\leq n \gamma \bigg(\frac{|\boldsymbol{\mathfrak{t}}-\boldsymbol{\mathfrak{s}}|}{1-\theta}\bigg), \end{align*} $$
$$ \begin{align*} \log \bigg|\frac{(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}{(D_yf^{\boldsymbol{\mathfrak{s}}}_{{\boldsymbol{\omega}}} )_{\mathit{ii}}}\bigg|&=\sum_{k=1}^n (a_{\omega_k,i}(f^{\boldsymbol{\mathfrak{t}}}_{\sigma^k{{\boldsymbol{\omega}}}}(y))- a_{\omega_k,i}(f^{\boldsymbol{\mathfrak{s}}}_{\sigma^k{{\boldsymbol{\omega}}}}(y))\\ &\leq n \gamma \bigg(\frac{|\boldsymbol{\mathfrak{t}}-\boldsymbol{\mathfrak{s}}|}{1-\theta}\bigg), \end{align*} $$
where in the second inequality, we have used the fact that
![]() $|f^{\boldsymbol {\mathfrak {t}}}_{\sigma ^k{{\boldsymbol {\omega }}}}(y)-f^{\boldsymbol {\mathfrak {s}}}_{\sigma ^k{{\boldsymbol {\omega }}}}(y)|\leq ({|\boldsymbol {\mathfrak {t}}-\boldsymbol {\mathfrak {s}}|})/({1-\theta })$
(which follows from (4.9)). This proves (4.16).
$|f^{\boldsymbol {\mathfrak {t}}}_{\sigma ^k{{\boldsymbol {\omega }}}}(y)-f^{\boldsymbol {\mathfrak {s}}}_{\sigma ^k{{\boldsymbol {\omega }}}}(y)|\leq ({|\boldsymbol {\mathfrak {t}}-\boldsymbol {\mathfrak {s}}|})/({1-\theta })$
(which follows from (4.9)). This proves (4.16).
Step 3. Set
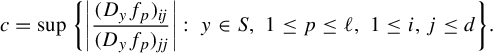 $$ \begin{align} c=\sup\bigg\{\bigg|\frac{(D_yf_p)_{\mathit{ij}}}{(D_yf_p)_{\mathit{jj}}}\bigg|:\; y\in S,\; 1\leq p\leq \ell,\; 1\leq i,j\leq d\bigg\}. \end{align} $$
$$ \begin{align} c=\sup\bigg\{\bigg|\frac{(D_yf_p)_{\mathit{ij}}}{(D_yf_p)_{\mathit{jj}}}\bigg|:\; y\in S,\; 1\leq p\leq \ell,\; 1\leq i,j\leq d\bigg\}. \end{align} $$
Then
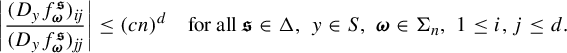 $$ \begin{align} \bigg|\frac{(D_yf_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}})_{\mathit{ij}}}{(D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}})_{\mathit{jj}}} \bigg|\leq (cn)^d \quad \text{for all } \boldsymbol{\mathfrak{s}}\in \Delta,\; y\in S,\; \boldsymbol{\omega}\in \Sigma_n,\; 1\leq i,j\leq d. \end{align} $$
$$ \begin{align} \bigg|\frac{(D_yf_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}})_{\mathit{ij}}}{(D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}})_{\mathit{jj}}} \bigg|\leq (cn)^d \quad \text{for all } \boldsymbol{\mathfrak{s}}\in \Delta,\; y\in S,\; \boldsymbol{\omega}\in \Sigma_n,\; 1\leq i,j\leq d. \end{align} $$
To see this, we simply notice that
![]() $D_yf_{{\boldsymbol {\omega }}}^{\boldsymbol {\mathfrak {s}}}=\prod _{k=1}^n D_{f^{\boldsymbol {\mathfrak {s}}}_{\sigma ^k {\boldsymbol {\omega }}}(y)}f_{\omega _k}$
and apply Lemma 4.5.
$D_yf_{{\boldsymbol {\omega }}}^{\boldsymbol {\mathfrak {s}}}=\prod _{k=1}^n D_{f^{\boldsymbol {\mathfrak {s}}}_{\sigma ^k {\boldsymbol {\omega }}}(y)}f_{\omega _k}$
and apply Lemma 4.5.
Step 4. Let c and
![]() $C_n$
be defined as in (4.17) and (4.11). Then for
$C_n$
be defined as in (4.17) and (4.11). Then for
![]() $\boldsymbol {\mathfrak {t}}\in \Delta $
,
$\boldsymbol {\mathfrak {t}}\in \Delta $
,
![]() $y, z_1,\ldots , z_d\in S$
,
$y, z_1,\ldots , z_d\in S$
,
![]() $\boldsymbol {\omega }\in \Sigma _n$
and
$\boldsymbol {\omega }\in \Sigma _n$
and
![]() $1\leq k,j\leq d$
,
$1\leq k,j\leq d$
,
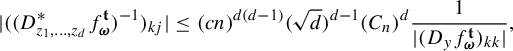 $$ \begin{align} |((D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})^{-1})_{kj}| \leq (cn)^{d(d-1)}(\sqrt{d})^{d-1}(C_n)^d \frac{1}{|(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{kk}|}, \end{align} $$
$$ \begin{align} |((D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})^{-1})_{kj}| \leq (cn)^{d(d-1)}(\sqrt{d})^{d-1}(C_n)^d \frac{1}{|(D_yf^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{kk}|}, \end{align} $$
where
![]() $D_{z_1,\ldots , z_d}^*g$
is defined as in (4.1).
$D_{z_1,\ldots , z_d}^*g$
is defined as in (4.1).
To prove (4.19), notice that for all
![]() $1\leq k,j\leq d$
,
$1\leq k,j\leq d$
,
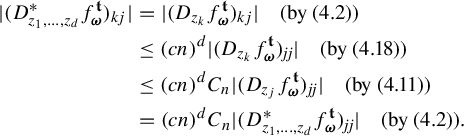 $$ \begin{align*} |(D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{kj}|&= |(D_{z_k}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{kj}| \quad \text{(by (4.2))}\\ &\leq (cn)^d |(D_{z_k}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{\mathit{jj}}| \quad \text{(by (4.18))}\\ &\leq (cn)^d C_n |(D_{z_j}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{\mathit{jj}}| \quad \text{(by (4.11))}\\ &= (cn)^d C_n |(D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{\mathit{jj}}|\quad \text{(by (4.2))}. \end{align*} $$
$$ \begin{align*} |(D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{kj}|&= |(D_{z_k}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{kj}| \quad \text{(by (4.2))}\\ &\leq (cn)^d |(D_{z_k}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{\mathit{jj}}| \quad \text{(by (4.18))}\\ &\leq (cn)^d C_n |(D_{z_j}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{\mathit{jj}}| \quad \text{(by (4.11))}\\ &= (cn)^d C_n |(D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{\mathit{jj}}|\quad \text{(by (4.2))}. \end{align*} $$
Applying Lemma 4.4 (in which we replace c by
![]() $(cn)^dC_n$
and take
$(cn)^dC_n$
and take
![]() $A=D_{z_1,\ldots , z_d}^*f^{\boldsymbol {\mathfrak {t}}}_{{\boldsymbol {\omega }}}$
), we obtain
$A=D_{z_1,\ldots , z_d}^*f^{\boldsymbol {\mathfrak {t}}}_{{\boldsymbol {\omega }}}$
), we obtain
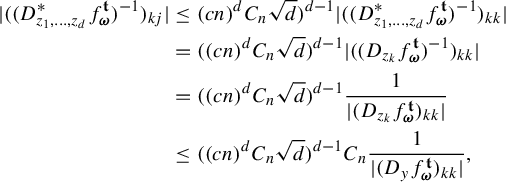 $$ \begin{align*} \begin{split} |((D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})^{-1})_{kj}|&\leq (cn)^dC_n\sqrt{d})^{d-1}|((D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})^{-1})_{kk}|\\ & =((cn)^dC_n\sqrt{d})^{d-1}|((D_{z_k}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})^{-1})_{kk}|\\ & =((cn)^dC_n\sqrt{d})^{d-1}\frac{1}{|(D_{z_k}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{kk}|}\\ &\leq ((cn)^dC_n\sqrt{d})^{d-1}C_n\frac{1}{|(D_{y}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{kk}|}, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} |((D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})^{-1})_{kj}|&\leq (cn)^dC_n\sqrt{d})^{d-1}|((D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})^{-1})_{kk}|\\ & =((cn)^dC_n\sqrt{d})^{d-1}|((D_{z_k}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})^{-1})_{kk}|\\ & =((cn)^dC_n\sqrt{d})^{d-1}\frac{1}{|(D_{z_k}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{kk}|}\\ &\leq ((cn)^dC_n\sqrt{d})^{d-1}C_n\frac{1}{|(D_{y}f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}})_{kk}|}, \end{split} \end{align*} $$
from which (4.19) follows.
Step 5. Now we are ready to prove (4.4). Let
![]() $\delta \in (0,r_0)$
. Write
$\delta \in (0,r_0)$
. Write
Then, for
![]() $\boldsymbol {\mathfrak {s}},\boldsymbol {\mathfrak {t}}\in \Delta $
with
$\boldsymbol {\mathfrak {s}},\boldsymbol {\mathfrak {t}}\in \Delta $
with
![]() $|\boldsymbol {\mathfrak {t}}-\boldsymbol {\mathfrak {s}}|\leq \delta $
and
$|\boldsymbol {\mathfrak {t}}-\boldsymbol {\mathfrak {s}}|\leq \delta $
and
![]() $1\leq i,j\leq d$
,
$1\leq i,j\leq d$
,
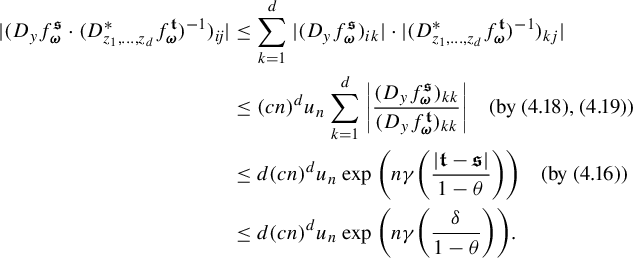 $$ \begin{align*} | (D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}}\cdot(D^*_{z_1,\ldots, z_d} f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{t}}})^{-1})_{\mathit{ij}}| &\leq \sum_{k=1}^d| (D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}})_{ik}|\cdot | (D^*_{z_1,\ldots, z_d} f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{t}}})^{-1})_{kj} |\\ &\leq (cn)^du_n\sum_{k=1}^d\bigg| \frac{(D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}})_{kk}}{(D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{t}}})_{kk}}\bigg|\quad \text{(by (4.18), (4.19))}\\ &\leq d(cn)^du_n\exp\bigg(n \gamma \bigg(\frac{|\boldsymbol{\mathfrak{t}}-\boldsymbol{\mathfrak{s}}|}{1-\theta}\bigg)\bigg)\quad \text{(by (4.16))}\\ &\leq d(cn)^du_n\exp\bigg(n \gamma \bigg(\frac{\delta}{1-\theta}\bigg)\bigg). \end{align*} $$
$$ \begin{align*} | (D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}}\cdot(D^*_{z_1,\ldots, z_d} f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{t}}})^{-1})_{\mathit{ij}}| &\leq \sum_{k=1}^d| (D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}})_{ik}|\cdot | (D^*_{z_1,\ldots, z_d} f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{t}}})^{-1})_{kj} |\\ &\leq (cn)^du_n\sum_{k=1}^d\bigg| \frac{(D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}})_{kk}}{(D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{t}}})_{kk}}\bigg|\quad \text{(by (4.18), (4.19))}\\ &\leq d(cn)^du_n\exp\bigg(n \gamma \bigg(\frac{|\boldsymbol{\mathfrak{t}}-\boldsymbol{\mathfrak{s}}|}{1-\theta}\bigg)\bigg)\quad \text{(by (4.16))}\\ &\leq d(cn)^du_n\exp\bigg(n \gamma \bigg(\frac{\delta}{1-\theta}\bigg)\bigg). \end{align*} $$
This implies that
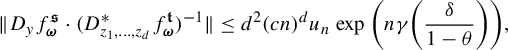 $$ \begin{align} \| D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}}\cdot(D^*_{z_1,\ldots, z_d} f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{t}}})^{-1}\|\leq d^2(cn)^du_n\exp\bigg(n \gamma \bigg(\frac{\delta}{1-\theta}\bigg)\bigg), \end{align} $$
$$ \begin{align} \| D_y f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}}\cdot(D^*_{z_1,\ldots, z_d} f_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{t}}})^{-1}\|\leq d^2(cn)^du_n\exp\bigg(n \gamma \bigg(\frac{\delta}{1-\theta}\bigg)\bigg), \end{align} $$
where we have used an easily checked fact that
for
![]() $A=(A_{\mathit {ij}})\in {\Bbb R}^{d\times d}$
.
$A=(A_{\mathit {ij}})\in {\Bbb R}^{d\times d}$
.
Set
![]() $h:(0,r_0)\to (0,\infty )$
by
$h:(0,r_0)\to (0,\infty )$
by
![]() $h(x)=x+ \gamma ({x}/({1-\theta }))$
. Since
$h(x)=x+ \gamma ({x}/({1-\theta }))$
. Since
there exists
![]() $C(\delta )>0$
such that
$C(\delta )>0$
such that
![]() $d^2(cn)^du_ne^{-n\delta }\leq C(\delta )$
for all
$d^2(cn)^du_ne^{-n\delta }\leq C(\delta )$
for all
![]() $n\geq 1$
. According to this fact and (4.20), we obtain the desired inequality
$n\geq 1$
. According to this fact and (4.20), we obtain the desired inequality
for later convenience, we may assume that
![]() $C(\delta )\geq 1$
.
$C(\delta )\geq 1$
.
4.2 Proof of Theorem 4.2
The following result plays a key part in our proof.
Lemma 4.7. Let
![]() $\{\mathcal F^{\boldsymbol {\mathfrak {t}}}\}_{\boldsymbol {\mathfrak {t}}\in \Delta }$
be a translational family of IFSs on a compact set
$\{\mathcal F^{\boldsymbol {\mathfrak {t}}}\}_{\boldsymbol {\mathfrak {t}}\in \Delta }$
be a translational family of IFSs on a compact set
![]() $S\subset {\Bbb R}^d$
generated by a
$S\subset {\Bbb R}^d$
generated by a
![]() $C^1$
IFS
$C^1$
IFS
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
. Suppose that (4.3) holds. Let
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
. Suppose that (4.3) holds. Let
![]() $\delta>0$
. Then there exists
$\delta>0$
. Then there exists
![]() $\widetilde {C}>0$
, which depends on
$\widetilde {C}>0$
, which depends on
![]() $\mathcal F$
and
$\mathcal F$
and
![]() $\delta $
such that the following holds. Let
$\delta $
such that the following holds. Let
![]() $\mathbf {a}=(a_n)_{n=1}^{\infty },\mathbf {b}=(b_n)_{n=1}^{\infty }\in \Sigma $
with
$\mathbf {a}=(a_n)_{n=1}^{\infty },\mathbf {b}=(b_n)_{n=1}^{\infty }\in \Sigma $
with
![]() $a_1\neq b_1$
, and let A be a real invertible
$a_1\neq b_1$
, and let A be a real invertible
![]() $d\times d$
matrix. Then for
$d\times d$
matrix. Then for
![]() $\boldsymbol {\mathfrak {s}}\in \Delta $
and
$\boldsymbol {\mathfrak {s}}\in \Delta $
and
![]() $r>0$
,
$r>0$
,
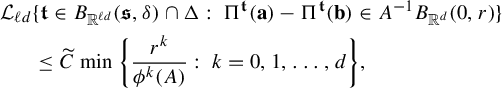 $$ \begin{align} \mathcal L_{\ell d}&\{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}}, \delta)\cap \Delta:\; \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in A^{-1}B_{{\Bbb R}^d}(0,r)\} \nonumber\\ &\leq \widetilde{C}\min\bigg\{\frac{r^k}{\phi^k(A)}:\; k=0,1,\ldots,d\bigg\}, \end{align} $$
$$ \begin{align} \mathcal L_{\ell d}&\{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}}, \delta)\cap \Delta:\; \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in A^{-1}B_{{\Bbb R}^d}(0,r)\} \nonumber\\ &\leq \widetilde{C}\min\bigg\{\frac{r^k}{\phi^k(A)}:\; k=0,1,\ldots,d\bigg\}, \end{align} $$
where
![]() $B_{{\Bbb R}^{\ell d}}(\cdot ,\cdot )$
and
$B_{{\Bbb R}^{\ell d}}(\cdot ,\cdot )$
and
![]() $B_{{\Bbb R}^d}(\cdot ,\cdot )$
stand for closed balls in
$B_{{\Bbb R}^d}(\cdot ,\cdot )$
stand for closed balls in
![]() ${\Bbb R}^{\ell d}$
and
${\Bbb R}^{\ell d}$
and
![]() ${\Bbb R}^{d}$
, respectively.
${\Bbb R}^{d}$
, respectively.
Since the proof of the above lemma is a little long, we will postpone it until we have finished the proof of Theorem 4.2.
Proof of Theorem 4.2 by assuming Lemma 4.7 Fix
![]() $\boldsymbol {\mathfrak {s}}\in \Delta $
and
$\boldsymbol {\mathfrak {s}}\in \Delta $
and
![]() $\delta \in (0,r_0)$
. Let
$\delta \in (0,r_0)$
. Let
![]() $\mathbf {i},\mathbf {j}\in \Sigma $
with
$\mathbf {i},\mathbf {j}\in \Sigma $
with
![]() $\mathbf {i}\neq \mathbf {j}$
. Set
$\mathbf {i}\neq \mathbf {j}$
. Set
Write
![]() $\mathbf {a}=\sigma ^n \mathbf {i}$
and
$\mathbf {a}=\sigma ^n \mathbf {i}$
and
![]() $\mathbf {b}=\sigma ^n \mathbf {j}$
. Clearly
$\mathbf {b}=\sigma ^n \mathbf {j}$
. Clearly
![]() $a_1\neq b_1$
.
$a_1\neq b_1$
.
Fix
![]() $y\in S$
. We claim that for
$y\in S$
. We claim that for
![]() $r>0$
,
$r>0$
,
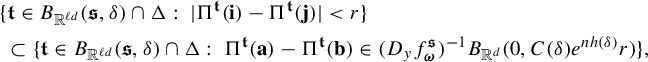 $$ \begin{align} &\{\boldsymbol{\mathfrak{t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{j})|< r\}\nonumber\\ &\text{}\; \subset \{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} B_{{\Bbb R}^d}(0,C(\delta)e^{nh(\delta)}r) \}, \end{align} $$
$$ \begin{align} &\{\boldsymbol{\mathfrak{t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{j})|< r\}\nonumber\\ &\text{}\; \subset \{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} B_{{\Bbb R}^d}(0,C(\delta)e^{nh(\delta)}r) \}, \end{align} $$
where
![]() $C(\delta )$
and
$C(\delta )$
and
![]() $h(\delta )$
are given as in Proposition 4.3.
$h(\delta )$
are given as in Proposition 4.3.
To show (4.22), let
![]() $\boldsymbol {\mathfrak {t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol {\mathfrak {s}},\delta )\cap \Delta $
so that
$\boldsymbol {\mathfrak {t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol {\mathfrak {s}},\delta )\cap \Delta $
so that
![]() $|\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {i})-\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {j})|<r$
. Notice that
$|\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {i})-\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {j})|<r$
. Notice that
Since S is convex, by the mean value theorem, there exist
![]() $z_1,\ldots , z_d\in S$
such that
$z_1,\ldots , z_d\in S$
such that
Hence
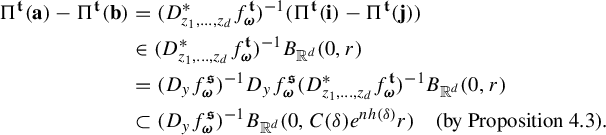 $$ \begin{align*} \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})&=(D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}})^{-1}(\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ j}))\\ &\in (D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}})^{-1}B_{{\Bbb R}^d}(0,r)\\ &= (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}} (D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}})^{-1}B_{{\Bbb R}^d}(0,r)\\ &\subset (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} B_{{\Bbb R}^d}(0,C(\delta)e^{nh(\delta)}r)\quad \text{(by Proposition~4.3).} \end{align*} $$
$$ \begin{align*} \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})&=(D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}})^{-1}(\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ j}))\\ &\in (D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}})^{-1}B_{{\Bbb R}^d}(0,r)\\ &= (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}} (D_{z_1,\ldots, z_d}^*f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}})^{-1}B_{{\Bbb R}^d}(0,r)\\ &\subset (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} B_{{\Bbb R}^d}(0,C(\delta)e^{nh(\delta)}r)\quad \text{(by Proposition~4.3).} \end{align*} $$
This proves (4.22).
By (4.22) and Lemma 4.7, we see that
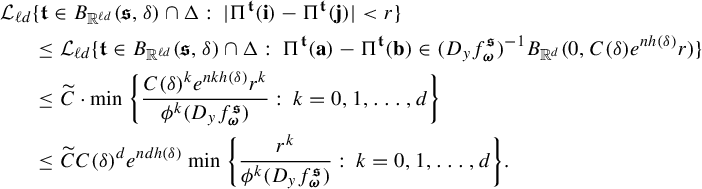 $$ \begin{align*} \begin{split} \mathcal L_{\ell d}&\{\boldsymbol{\mathfrak{t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{j})|< r\}\\ &\leq \mathcal L_{\ell d} \{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} B_{{\Bbb R}^d}(0,C(\delta)e^{nh(\delta)}r) \}\\ &\leq \widetilde{C}\cdot\min\bigg\{\frac{C(\delta)^ke^{nkh(\delta)}r^k}{\phi^k(D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})}:\; k=0,1,\ldots,d\bigg\}\\ &\leq \widetilde{C}C(\delta)^de^{ndh(\delta)}\min\bigg\{\frac{r^k}{\phi^k(D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})}:\; k=0,1,\ldots,d\bigg\}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \mathcal L_{\ell d}&\{\boldsymbol{\mathfrak{t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{j})|< r\}\\ &\leq \mathcal L_{\ell d} \{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} B_{{\Bbb R}^d}(0,C(\delta)e^{nh(\delta)}r) \}\\ &\leq \widetilde{C}\cdot\min\bigg\{\frac{C(\delta)^ke^{nkh(\delta)}r^k}{\phi^k(D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})}:\; k=0,1,\ldots,d\bigg\}\\ &\leq \widetilde{C}C(\delta)^de^{ndh(\delta)}\min\bigg\{\frac{r^k}{\phi^k(D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})}:\; k=0,1,\ldots,d\bigg\}. \end{split} \end{align*} $$
Since
![]() $y\in S$
is arbitrary and
$y\in S$
is arbitrary and
![]() $\Pi ^{\boldsymbol {\mathfrak {s}}}(\Sigma )\subset S$
, recalling
$\Pi ^{\boldsymbol {\mathfrak {s}}}(\Sigma )\subset S$
, recalling
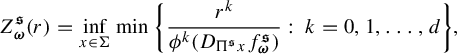 $$ \begin{align*} Z_{{\boldsymbol{\omega}}}^{\boldsymbol{\mathfrak{s}}}(r)= \inf_{x\in \Sigma} \min\bigg \{ \frac{r^k}{ \phi^k (D_{\Pi^{\boldsymbol{\mathfrak{s}}} x}f^{\boldsymbol{\mathfrak{s}}}_{{\boldsymbol{\omega}}} ) }:\; k=0, 1,\ldots, d\bigg\}, \end{align*} $$
$$ \begin{align*} Z_{{\boldsymbol{\omega}}}^{\boldsymbol{\mathfrak{s}}}(r)= \inf_{x\in \Sigma} \min\bigg \{ \frac{r^k}{ \phi^k (D_{\Pi^{\boldsymbol{\mathfrak{s}}} x}f^{\boldsymbol{\mathfrak{s}}}_{{\boldsymbol{\omega}}} ) }:\; k=0, 1,\ldots, d\bigg\}, \end{align*} $$
it follows that
This completes the proof of the theorem by letting
![]() $c_{\delta }=\widetilde {C}C(\delta )^d$
and
$c_{\delta }=\widetilde {C}C(\delta )^d$
and
![]() $\psi (\delta )=dh(\delta )$
.
$\psi (\delta )=dh(\delta )$
.
In what follows we prove Lemma 4.7. To this end, we first prove an elementary geometric lemma.
Lemma 4.8. Let A be a real invertible
![]() $d\times d$
matrix. Then for
$d\times d$
matrix. Then for
![]() $r_1,r_2>0$
,
$r_1,r_2>0$
,
 $$ \begin{align*}\mathcal L_{d}((A^{-1}B_{{\Bbb R}^d}(0,r_1))\cap B_{{\Bbb R}^d}(0,r_2))\leq 2^d \min\bigg\{ \frac{r_1^kr_2^{d-k}}{\phi^k(A)}:\; k=0,1,\ldots, d\bigg\}, \end{align*} $$
$$ \begin{align*}\mathcal L_{d}((A^{-1}B_{{\Bbb R}^d}(0,r_1))\cap B_{{\Bbb R}^d}(0,r_2))\leq 2^d \min\bigg\{ \frac{r_1^kr_2^{d-k}}{\phi^k(A)}:\; k=0,1,\ldots, d\bigg\}, \end{align*} $$
where
![]() $\phi ^s(\cdot )$
is the singular value function defined as in (2.5).
$\phi ^s(\cdot )$
is the singular value function defined as in (2.5).
Proof Let
![]() $\alpha _1\geq \cdots \geq \alpha _d$
be the singular values of A. Clearly the set
$\alpha _1\geq \cdots \geq \alpha _d$
be the singular values of A. Clearly the set
is contained in a rectangular parallelepiped with sides
![]() $2\min \{r_1/\alpha _i, r_2\}$
,
$2\min \{r_1/\alpha _i, r_2\}$
,
![]() $i=1,\ldots , d$
. It follows that
$i=1,\ldots , d$
. It follows that
 $$ \begin{align*} \mathcal L_d((A^{-1}B_{{\Bbb R}^d}(0,r_1))\cap B_{{\Bbb R}^d}(0,r_2))&\leq 2^d\prod_{i=1}^d\min\bigg\{\frac{r_1}{\alpha_i},\; r_2\bigg\}\\ &= 2^d \min\bigg\{\frac{r_1^kr_2^{d-k}}{\alpha_1\ldots \alpha_k}:\; k=0,1,\ldots, d\bigg\}\\ &= 2^d \min\bigg\{\frac{r_1^kr_2^{d-k}}{\phi^k(A)}:\; k=0,1,\ldots, d\bigg\}. \\[-42pt] \end{align*} $$
$$ \begin{align*} \mathcal L_d((A^{-1}B_{{\Bbb R}^d}(0,r_1))\cap B_{{\Bbb R}^d}(0,r_2))&\leq 2^d\prod_{i=1}^d\min\bigg\{\frac{r_1}{\alpha_i},\; r_2\bigg\}\\ &= 2^d \min\bigg\{\frac{r_1^kr_2^{d-k}}{\alpha_1\ldots \alpha_k}:\; k=0,1,\ldots, d\bigg\}\\ &= 2^d \min\bigg\{\frac{r_1^kr_2^{d-k}}{\phi^k(A)}:\; k=0,1,\ldots, d\bigg\}. \\[-42pt] \end{align*} $$
Proof of Lemma 4.7 Let
![]() $\mathbf {a}=(a_n)_{n=1}^{\infty },\mathbf {b}=(b_n)_{n=1}^{\infty }\in \Sigma $
with
$\mathbf {a}=(a_n)_{n=1}^{\infty },\mathbf {b}=(b_n)_{n=1}^{\infty }\in \Sigma $
with
![]() $a_1\neq b_1$
. Without loss of generality, we assume that
$a_1\neq b_1$
. Without loss of generality, we assume that
Define
![]() $g:\Delta \to {\Bbb R}^d$
by
$g:\Delta \to {\Bbb R}^d$
by
Recall that we have used the notation
![]() $ \boldsymbol {\mathfrak {t}} =(\mathbf {t}_1 , \ldots , \mathbf {t}_{\ell } )\in \Delta \subset \mathbb {R}^{\ell d }$
with
$ \boldsymbol {\mathfrak {t}} =(\mathbf {t}_1 , \ldots , \mathbf {t}_{\ell } )\in \Delta \subset \mathbb {R}^{\ell d }$
with
For
![]() $\boldsymbol {\mathfrak {t}} =(\mathbf {t}_1, \ldots , \mathbf {t}_{\ell } )\in \Delta $
and
$\boldsymbol {\mathfrak {t}} =(\mathbf {t}_1, \ldots , \mathbf {t}_{\ell } )\in \Delta $
and
![]() $k\in \{1,\ldots , \ell \}$
, let
$k\in \{1,\ldots , \ell \}$
, let
![]() $({\partial g}/{\partial \mathbf {t} _k})(\boldsymbol {\mathfrak {t}} )$
denote the Jacobian matrix of the following map from
$({\partial g}/{\partial \mathbf {t} _k})(\boldsymbol {\mathfrak {t}} )$
denote the Jacobian matrix of the following map from
![]() ${\Bbb R}^d$
to
${\Bbb R}^d$
to
![]() ${\Bbb R}^d$
:
${\Bbb R}^d$
:
Write
![]() $\mathbf {I}=\mathbf {I}_{d}:=\mathrm {diag}(\underbrace {1,\ldots ,1}_{d})$
. First observe that for every
$\mathbf {I}=\mathbf {I}_{d}:=\mathrm {diag}(\underbrace {1,\ldots ,1}_{d})$
. First observe that for every
![]() $n\in {\Bbb N}$
and
$n\in {\Bbb N}$
and
![]() ${\mathbf {i}=(i_k)_{k=1}^{\infty }\in \Sigma }$
,
${\mathbf {i}=(i_k)_{k=1}^{\infty }\in \Sigma }$
,
It follows that for
![]() $k\in \{1,\ldots , \ell \}$
,
$k\in \{1,\ldots , \ell \}$
,
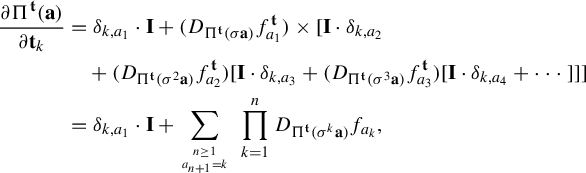 $$ \begin{align} \frac{\partial\Pi^{\boldsymbol{\mathfrak{t}}} (\mathbf{a})}{\partial\mathbf{t}_{k}} &= \delta_{k, a_1} \cdot \mathbf{I}+(D_{\Pi^{\boldsymbol{\mathfrak{t}}}(\sigma\mathbf{a})}f_{a_1}^{\boldsymbol{\mathfrak{t}}}) \times [\mathbf{I}\cdot\delta_{k, a_2}\nonumber\\ &\quad+(D_{\Pi^{\boldsymbol{\mathfrak{t}}} (\sigma^2\mathbf{a})} f_{a_2}^{\boldsymbol{\mathfrak{t}}})[\mathbf{I}\cdot\delta_{k, a_3}+ (D_{\Pi^{\boldsymbol{\mathfrak{t}}}(\sigma^3\mathbf{a})}f_{a_3}^{\boldsymbol{\mathfrak{t}}}) [\mathbf{I}\cdot\delta_{k, a_4}+\cdots] ]] \nonumber\\ &= \delta_{k, a_1} \cdot \mathbf{I}+ \sum\limits_{n \geq 1 \atop a_{n+1}=k}\ \prod_{k=1}^{n}D_{\Pi^{\boldsymbol{\mathfrak{t}} }(\sigma^k\mathbf{a})}f_{a_k}, \end{align} $$
$$ \begin{align} \frac{\partial\Pi^{\boldsymbol{\mathfrak{t}}} (\mathbf{a})}{\partial\mathbf{t}_{k}} &= \delta_{k, a_1} \cdot \mathbf{I}+(D_{\Pi^{\boldsymbol{\mathfrak{t}}}(\sigma\mathbf{a})}f_{a_1}^{\boldsymbol{\mathfrak{t}}}) \times [\mathbf{I}\cdot\delta_{k, a_2}\nonumber\\ &\quad+(D_{\Pi^{\boldsymbol{\mathfrak{t}}} (\sigma^2\mathbf{a})} f_{a_2}^{\boldsymbol{\mathfrak{t}}})[\mathbf{I}\cdot\delta_{k, a_3}+ (D_{\Pi^{\boldsymbol{\mathfrak{t}}}(\sigma^3\mathbf{a})}f_{a_3}^{\boldsymbol{\mathfrak{t}}}) [\mathbf{I}\cdot\delta_{k, a_4}+\cdots] ]] \nonumber\\ &= \delta_{k, a_1} \cdot \mathbf{I}+ \sum\limits_{n \geq 1 \atop a_{n+1}=k}\ \prod_{k=1}^{n}D_{\Pi^{\boldsymbol{\mathfrak{t}} }(\sigma^k\mathbf{a})}f_{a_k}, \end{align} $$
where
![]() $\delta _{i,j}=1$
if
$\delta _{i,j}=1$
if
![]() $i=j$
and
$i=j$
and
![]() $0$
otherwise.
$0$
otherwise.
By (4.25) and the assumption (4.23), we see that for
![]() $k\in \{1,\ldots , \ell \}$
,
$k\in \{1,\ldots , \ell \}$
,
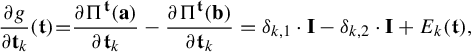 $$ \begin{align} \frac{\partial g}{{\partial\mathbf{t}_{k}}}(\boldsymbol{\mathfrak{t}} )\!&=\! \frac{\partial \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})}{\partial\boldsymbol{\mathfrak{t}} _{k}} - \frac{\partial \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})}{\partial\boldsymbol{\mathfrak{t}} _{k}}= \delta_{k, 1} \cdot \mathbf{I}-\delta_{k, 2} \cdot \mathbf{I} + E_{k}(\boldsymbol{\mathfrak{t}} ) , \end{align} $$
$$ \begin{align} \frac{\partial g}{{\partial\mathbf{t}_{k}}}(\boldsymbol{\mathfrak{t}} )\!&=\! \frac{\partial \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})}{\partial\boldsymbol{\mathfrak{t}} _{k}} - \frac{\partial \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})}{\partial\boldsymbol{\mathfrak{t}} _{k}}= \delta_{k, 1} \cdot \mathbf{I}-\delta_{k, 2} \cdot \mathbf{I} + E_{k}(\boldsymbol{\mathfrak{t}} ) , \end{align} $$
where
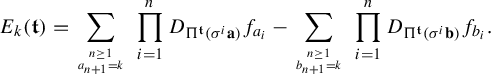 $$ \begin{align} E_{k}(\boldsymbol{\mathfrak{t}} ) = \sum\limits_{n \geq 1 \atop a_{n+1}=k}\ \prod_{i=1}^{n}D_{\Pi^{\boldsymbol{\mathfrak{t}} }(\sigma^i\mathbf{a})}f_{a_i} - \sum\limits_{n \geq 1 \atop b_{n+1}=k}\ \prod_{i=1}^{n}D_{\Pi^{\boldsymbol{\mathfrak{t}} }(\sigma^i\mathbf{b})}f_{b_i}. \end{align} $$
$$ \begin{align} E_{k}(\boldsymbol{\mathfrak{t}} ) = \sum\limits_{n \geq 1 \atop a_{n+1}=k}\ \prod_{i=1}^{n}D_{\Pi^{\boldsymbol{\mathfrak{t}} }(\sigma^i\mathbf{a})}f_{a_i} - \sum\limits_{n \geq 1 \atop b_{n+1}=k}\ \prod_{i=1}^{n}D_{\Pi^{\boldsymbol{\mathfrak{t}} }(\sigma^i\mathbf{b})}f_{b_i}. \end{align} $$
Recall that
![]() $\rho =\max \nolimits _{i\neq j}(\rho _i+\rho _j)<1$
with
$\rho =\max \nolimits _{i\neq j}(\rho _i+\rho _j)<1$
with
![]() $\rho _i:=\max \nolimits _{z\in S}\|D_zf_i\|$
.
$\rho _i:=\max \nolimits _{z\in S}\|D_zf_i\|$
.
Lemma 4.9. There exists
![]() $k^*=k^*(\mathbf {a},\mathbf {b})\in \{1,2\}$
such that
$k^*=k^*(\mathbf {a},\mathbf {b})\in \{1,2\}$
such that
![]() $\|E_{k^*}(\boldsymbol {\mathfrak {t}} )\| < \rho $
for all
$\|E_{k^*}(\boldsymbol {\mathfrak {t}} )\| < \rho $
for all
![]() $\boldsymbol {\mathfrak {t}} \in \Delta $
.
$\boldsymbol {\mathfrak {t}} \in \Delta $
.
Proof Our argument is based on an idea of Boris Solomyak, which was used to prove a corresponding statement for self-affine IFSs [Reference Bárány, Simon and Solomyak3, Theorem 9.1.2].
By (4.27), for each
![]() $k\in \{1,2\}$
and
$k\in \{1,2\}$
and
![]() $\boldsymbol {\mathfrak {t}} \in \Delta $
,
$\boldsymbol {\mathfrak {t}} \in \Delta $
,
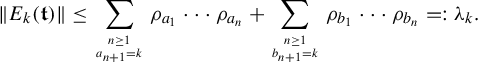
Clearly,
![]() $\unicode{x3bb} _k$
(
$\unicode{x3bb} _k$
(
![]() $k=1,2$
) only depend on
$k=1,2$
) only depend on
![]() $\mathbf {a}$
and
$\mathbf {a}$
and
![]() $\mathbf {b}$
.
$\mathbf {b}$
.
Notice that
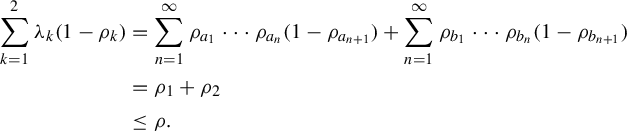
This implies that one of
![]() $\unicode{x3bb} _1,\unicode{x3bb} _2$
is smaller than
$\unicode{x3bb} _1,\unicode{x3bb} _2$
is smaller than
![]() $\rho $
; otherwise, since
$\rho $
; otherwise, since
![]() $\rho _1+\rho _2\leq \rho <1$
, it follows that
$\rho _1+\rho _2\leq \rho <1$
, it follows that
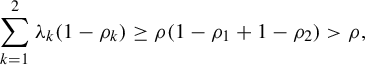
which contradicts (4.29). Now set
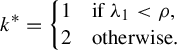
Then
![]() $\unicode{x3bb} _{k^*}<\rho $
. Since
$\unicode{x3bb} _{k^*}<\rho $
. Since
![]() $\unicode{x3bb} _1, \unicode{x3bb} _2$
only depend on
$\unicode{x3bb} _1, \unicode{x3bb} _2$
only depend on
![]() $\mathbf {a}$
and
$\mathbf {a}$
and
![]() $\mathbf {b}$
, so does
$\mathbf {b}$
, so does
![]() $k^*$
. By (4.28),
$k^*$
. By (4.28),
for all
![]() $\boldsymbol {\mathfrak {t}}\in \Delta $
.
$\boldsymbol {\mathfrak {t}}\in \Delta $
.
In what follows, we always let
![]() $k^*=k^*(\mathbf {a}, \mathbf {b})\in \{1,2\}$
be given as in Lemma 4.9.
$k^*=k^*(\mathbf {a}, \mathbf {b})\in \{1,2\}$
be given as in Lemma 4.9.
Lemma 4.10. For all
![]() $\boldsymbol {\mathfrak {t}} \in \Delta $
,
$\boldsymbol {\mathfrak {t}} \in \Delta $
,
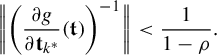 $$ \begin{align} \bigg\|\bigg( \frac{\partial g}{{\partial\mathbf{t}_{k^* }}}(\boldsymbol{\mathfrak{t}} )\bigg)^{-1} \bigg\| < \frac{1}{1-\rho}. \end{align} $$
$$ \begin{align} \bigg\|\bigg( \frac{\partial g}{{\partial\mathbf{t}_{k^* }}}(\boldsymbol{\mathfrak{t}} )\bigg)^{-1} \bigg\| < \frac{1}{1-\rho}. \end{align} $$
Proof Without loss of generality, we assume that
![]() $k^*=1$
. The proof is similar in the case when
$k^*=1$
. The proof is similar in the case when
![]() $k^*=2$
.
$k^*=2$
.
Let
![]() $\boldsymbol {\mathfrak {t}} \in \Delta $
. By Lemma 4.9,
$\boldsymbol {\mathfrak {t}} \in \Delta $
. By Lemma 4.9,
![]() $\|E_1(\boldsymbol {\mathfrak {t}} )\|< \rho <1$
. Thanks to (4.26),
$\|E_1(\boldsymbol {\mathfrak {t}} )\|< \rho <1$
. Thanks to (4.26),
where
![]() $\mathbf {I}=\mathrm {diag}(\underbrace {1,\ldots ,1}_d)$
. Since
$\mathbf {I}=\mathrm {diag}(\underbrace {1,\ldots ,1}_d)$
. Since
![]() $\|E_1(\boldsymbol {\mathfrak {t}} )\|< \rho <1$
, we see that
$\|E_1(\boldsymbol {\mathfrak {t}} )\|< \rho <1$
, we see that
![]() ${\partial g}/{{\partial \mathbf {t}_{1 }}}(\boldsymbol {\mathfrak {t}} )$
is invertible with
${\partial g}/{{\partial \mathbf {t}_{1 }}}(\boldsymbol {\mathfrak {t}} )$
is invertible with
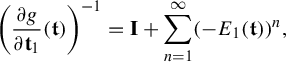 $$ \begin{align*}\bigg(\frac{\partial g}{{\partial\mathbf{t}_{1 }}}(\boldsymbol{\mathfrak{t}})\bigg )^{-1}=\mathbf{I}+ \sum_{n=1}^{\infty} (-E_1(\boldsymbol{\mathfrak{t}} ))^n, \end{align*} $$
$$ \begin{align*}\bigg(\frac{\partial g}{{\partial\mathbf{t}_{1 }}}(\boldsymbol{\mathfrak{t}})\bigg )^{-1}=\mathbf{I}+ \sum_{n=1}^{\infty} (-E_1(\boldsymbol{\mathfrak{t}} ))^n, \end{align*} $$
from which we obtain that
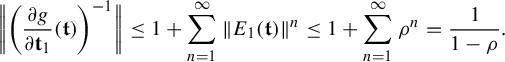 $$ \begin{align} \bigg\|\bigg( \frac{\partial g}{{\partial\mathbf{t}_{1 }}}(\boldsymbol{\mathfrak{t}} )\bigg)^{-1} \bigg\|\leq 1+\sum_{n=1}^{\infty} \|E_1(\boldsymbol{\mathfrak{t}} )\|^n\leq 1+\sum_{n=1}^{\infty} \rho^n=\frac{1}{1-\rho}. \end{align} $$
$$ \begin{align} \bigg\|\bigg( \frac{\partial g}{{\partial\mathbf{t}_{1 }}}(\boldsymbol{\mathfrak{t}} )\bigg)^{-1} \bigg\|\leq 1+\sum_{n=1}^{\infty} \|E_1(\boldsymbol{\mathfrak{t}} )\|^n\leq 1+\sum_{n=1}^{\infty} \rho^n=\frac{1}{1-\rho}. \end{align} $$
Next we introduce two mappings
![]() $T_1, T_2: \Delta \to \mathbb {R}^{\ell d}$
by
$T_1, T_2: \Delta \to \mathbb {R}^{\ell d}$
by
where
![]() $\boldsymbol {\mathfrak {t}}=(\mathbf {t}_{1},\ldots , \mathbf {t}_{\ell })$
. Recall that
$\boldsymbol {\mathfrak {t}}=(\mathbf {t}_{1},\ldots , \mathbf {t}_{\ell })$
. Recall that
![]() $g(\boldsymbol {\mathfrak {t}})=\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {a})-\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {b})$
.
$g(\boldsymbol {\mathfrak {t}})=\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {a})-\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {b})$
.
Lemma 4.11. Let
![]() $k^*=k^*(\mathbf {a}, \mathbf {b})\in \{1,2\}$
be given as in Lemma 4.9. Then the following properties hold.
$k^*=k^*(\mathbf {a}, \mathbf {b})\in \{1,2\}$
be given as in Lemma 4.9. Then the following properties hold.
-
(i) The mapping
 $T_{k^*}:\;\Delta \to {\Bbb R}^{\ell d}$
is injective.
$T_{k^*}:\;\Delta \to {\Bbb R}^{\ell d}$
is injective. -
(ii) For each
 $\boldsymbol {\mathfrak {t}}\in \Delta $
, (4.34)
$\boldsymbol {\mathfrak {t}}\in \Delta $
, (4.34) $$ \begin{align} |\!\det(( D_{\boldsymbol{\mathfrak{t}}}T_{k^*})^{-1}) |<\bigg(\frac{1}{1-\rho}\bigg)^d. \end{align} $$
$$ \begin{align} |\!\det(( D_{\boldsymbol{\mathfrak{t}}}T_{k^*})^{-1}) |<\bigg(\frac{1}{1-\rho}\bigg)^d. \end{align} $$
Proof Without loss of generality, we may assume that
![]() $k^*=1$
. Then by Lemma 4.9 and (4.33),
$k^*=1$
. Then by Lemma 4.9 and (4.33),
for
![]() $\boldsymbol {\mathfrak {t}}=(\mathbf {t}_{1}, \ldots , \mathbf {t}_{\ell })\in \Delta $
. Hence to prove (i), it suffices to show that for given
$\boldsymbol {\mathfrak {t}}=(\mathbf {t}_{1}, \ldots , \mathbf {t}_{\ell })\in \Delta $
. Hence to prove (i), it suffices to show that for given
![]() $\mathbf {t}_{2}, \ldots , \mathbf {t}_{\ell }\in {\Bbb R}^d$
with
$\mathbf {t}_{2}, \ldots , \mathbf {t}_{\ell }\in {\Bbb R}^d$
with
![]() $\sum _{i=2}^{\ell } |\mathbf {t}_{2}|^2<r_0^2$
, the mapping
$\sum _{i=2}^{\ell } |\mathbf {t}_{2}|^2<r_0^2$
, the mapping
is injective on
![]() $\Delta _1:=\{\mathbf {t}_1\in {\Bbb R}^d:\; |\mathbf {t}_1|<\sqrt {r_0^2-\sum _{i=2}^{\ell } |\mathbf {t}_{i}|^2}\}$
. To this end, define
$\Delta _1:=\{\mathbf {t}_1\in {\Bbb R}^d:\; |\mathbf {t}_1|<\sqrt {r_0^2-\sum _{i=2}^{\ell } |\mathbf {t}_{i}|^2}\}$
. To this end, define
![]() $\psi :\; \Delta _1\to {\Bbb R}^d$
by
$\psi :\; \Delta _1\to {\Bbb R}^d$
by
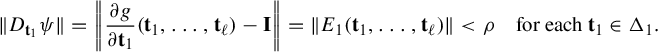 $$ \begin{align*}\|D_{\mathbf{t}_1}\psi\|=\bigg\|\frac{\partial g}{\partial \mathbf{t}_1}(\mathbf{t}_{1}, \ldots, \mathbf{t}_{\ell })-\mathbf{I}\bigg\|=\|E_1(\mathbf{t}_{1}, \ldots, \mathbf{t}_{\ell })\|<\rho \quad \text{for each } \mathbf{t}_{1}\in \Delta_1. \end{align*} $$
$$ \begin{align*}\|D_{\mathbf{t}_1}\psi\|=\bigg\|\frac{\partial g}{\partial \mathbf{t}_1}(\mathbf{t}_{1}, \ldots, \mathbf{t}_{\ell })-\mathbf{I}\bigg\|=\|E_1(\mathbf{t}_{1}, \ldots, \mathbf{t}_{\ell })\|<\rho \quad \text{for each } \mathbf{t}_{1}\in \Delta_1. \end{align*} $$
Since
![]() $\Delta _1$
is a convex open subset of
$\Delta _1$
is a convex open subset of
![]() ${\Bbb R}^d$
, by [Reference Rudin42, Theorem 9.19], the above inequality implies that
${\Bbb R}^d$
, by [Reference Rudin42, Theorem 9.19], the above inequality implies that
for all distinct
![]() $\mathbf {t}_1, \mathbf {s_1}\in \Delta _1$
. It follows that for distinct
$\mathbf {t}_1, \mathbf {s_1}\in \Delta _1$
. It follows that for distinct
![]() $\mathbf {t}_1, \mathbf {s_1}\in \Delta _1$
,
$\mathbf {t}_1, \mathbf {s_1}\in \Delta _1$
,
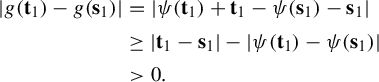 $$ \begin{align*} |g(\mathbf{t}_1)-g(\mathbf{s}_1)|&=|\psi(\mathbf{t}_1)+\mathbf{t}_1-\psi(\mathbf{s}_1)-\mathbf{s}_1|\\ &\geq |\mathbf{t}_1-\mathbf{s}_1|-|\psi(\mathbf{t}_1)-\psi(\mathbf{s}_1)|\\ &> 0. \end{align*} $$
$$ \begin{align*} |g(\mathbf{t}_1)-g(\mathbf{s}_1)|&=|\psi(\mathbf{t}_1)+\mathbf{t}_1-\psi(\mathbf{s}_1)-\mathbf{s}_1|\\ &\geq |\mathbf{t}_1-\mathbf{s}_1|-|\psi(\mathbf{t}_1)-\psi(\mathbf{s}_1)|\\ &> 0. \end{align*} $$
This proves (i).
To prove (ii), notice that
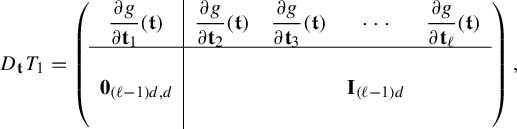 $$ \begin{align*} D_{\boldsymbol{\mathfrak{t}}}T_{1}=\left(\begin{array}{c|cccc} \displaystyle\frac{\partial{g}}{\partial{\mathbf{t}_1}}(\boldsymbol{\mathfrak{t}}) & \displaystyle\frac{\partial{g}}{\partial{\mathbf{t}_2}}(\boldsymbol{\mathfrak{t}}) & \displaystyle\frac{\partial{g}}{\partial{\mathbf{t}_3}}(\boldsymbol{\mathfrak{t}}) & \cdots & \displaystyle\frac{\partial{g}}{\partial{\mathbf{t}_{\ell }}}(\boldsymbol{\mathfrak{t}}) \\\hline & & & & \\ \mathbf{0}_{(\ell -1)d,d} & & & \mathbf{I}_{(\ell -1)d} & \\ & & & & \end{array}\right),\end{align*} $$
$$ \begin{align*} D_{\boldsymbol{\mathfrak{t}}}T_{1}=\left(\begin{array}{c|cccc} \displaystyle\frac{\partial{g}}{\partial{\mathbf{t}_1}}(\boldsymbol{\mathfrak{t}}) & \displaystyle\frac{\partial{g}}{\partial{\mathbf{t}_2}}(\boldsymbol{\mathfrak{t}}) & \displaystyle\frac{\partial{g}}{\partial{\mathbf{t}_3}}(\boldsymbol{\mathfrak{t}}) & \cdots & \displaystyle\frac{\partial{g}}{\partial{\mathbf{t}_{\ell }}}(\boldsymbol{\mathfrak{t}}) \\\hline & & & & \\ \mathbf{0}_{(\ell -1)d,d} & & & \mathbf{I}_{(\ell -1)d} & \\ & & & & \end{array}\right),\end{align*} $$
where
![]() $\mathbf {I}_{(\ell -1)d}:=\mathrm {diag}(\underbrace {1, \ldots , 1}_{(\ell -1)d})$
and
$\mathbf {I}_{(\ell -1)d}:=\mathrm {diag}(\underbrace {1, \ldots , 1}_{(\ell -1)d})$
and
![]() $\mathbf {0}_{(\ell -1)d,d}$
is the
$\mathbf {0}_{(\ell -1)d,d}$
is the
![]() $((\ell -1)d)\times d$
all-zero matrix. That is,
$((\ell -1)d)\times d$
all-zero matrix. That is,
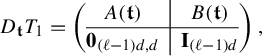 $$ \begin{align*} D_{\boldsymbol{\mathfrak{t}}}T_{1}=\left(\begin{array}{@{}c|c@{}}A(\boldsymbol{\mathfrak{t}})& B(\boldsymbol{\mathfrak{t}})\\ \hline \mathbf{0}_{(\ell-1)d, d}&\mathbf{I}_{(\ell-1)d}\end{array}\right), \end{align*} $$
$$ \begin{align*} D_{\boldsymbol{\mathfrak{t}}}T_{1}=\left(\begin{array}{@{}c|c@{}}A(\boldsymbol{\mathfrak{t}})& B(\boldsymbol{\mathfrak{t}})\\ \hline \mathbf{0}_{(\ell-1)d, d}&\mathbf{I}_{(\ell-1)d}\end{array}\right), \end{align*} $$
where
![]() $A(\boldsymbol {\mathfrak {t}})$
and
$A(\boldsymbol {\mathfrak {t}})$
and
![]() $B(\boldsymbol {\mathfrak {t}})$
are given by
$B(\boldsymbol {\mathfrak {t}})$
are given by
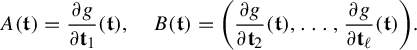 $$ \begin{align*} A(\boldsymbol{\mathfrak{t}})= \frac{\partial{g}}{\partial{\mathbf{t}_1}} (\boldsymbol{\mathfrak{t}} ), \quad B(\boldsymbol{\mathfrak{t}})= \bigg(\frac{\partial{g}}{\partial{\mathbf{t}_2}}(\boldsymbol{\mathfrak{t}}), \ldots, \frac{\partial{g}}{\partial{\mathbf{t}_{\ell }}}(\boldsymbol{\mathfrak{t}})\bigg). \end{align*} $$
$$ \begin{align*} A(\boldsymbol{\mathfrak{t}})= \frac{\partial{g}}{\partial{\mathbf{t}_1}} (\boldsymbol{\mathfrak{t}} ), \quad B(\boldsymbol{\mathfrak{t}})= \bigg(\frac{\partial{g}}{\partial{\mathbf{t}_2}}(\boldsymbol{\mathfrak{t}}), \ldots, \frac{\partial{g}}{\partial{\mathbf{t}_{\ell }}}(\boldsymbol{\mathfrak{t}})\bigg). \end{align*} $$
Hence, by Lemma 4.10,
![]() $A^{-1}(\boldsymbol {\mathfrak {t}} )$
exists and
$A^{-1}(\boldsymbol {\mathfrak {t}} )$
exists and
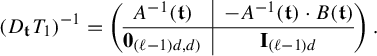 $$ \begin{align*} (D_{\boldsymbol{\mathfrak{t}}}T_{1})^{-1}=\left(\begin{array}{@{}c|c@{}}A^{-1}(\boldsymbol{\mathfrak{t}})&-A^{-1}(\boldsymbol{\mathfrak{t}})\cdot B(\boldsymbol{\mathfrak{t}})\\ \hline \mathbf{0}_{(\ell-1)d,d)} &\mathbf{I}_{(\ell-1)d}\end{array}\right). \end{align*} $$
$$ \begin{align*} (D_{\boldsymbol{\mathfrak{t}}}T_{1})^{-1}=\left(\begin{array}{@{}c|c@{}}A^{-1}(\boldsymbol{\mathfrak{t}})&-A^{-1}(\boldsymbol{\mathfrak{t}})\cdot B(\boldsymbol{\mathfrak{t}})\\ \hline \mathbf{0}_{(\ell-1)d,d)} &\mathbf{I}_{(\ell-1)d}\end{array}\right). \end{align*} $$
It follows that
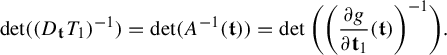 $$ \begin{align*} \det((D_{\boldsymbol{\mathfrak{t}}}T_{1})^{-1})= \det(A^{-1}(\boldsymbol{\mathfrak{t}})) =\det\bigg(\bigg(\frac{\partial g}{\partial\mathbf{t}_1}(\boldsymbol{\mathfrak{t}})\bigg)^{-1}\bigg). \end{align*} $$
$$ \begin{align*} \det((D_{\boldsymbol{\mathfrak{t}}}T_{1})^{-1})= \det(A^{-1}(\boldsymbol{\mathfrak{t}})) =\det\bigg(\bigg(\frac{\partial g}{\partial\mathbf{t}_1}(\boldsymbol{\mathfrak{t}})\bigg)^{-1}\bigg). \end{align*} $$
By the Hadamard’s inequality (see e.g. [Reference Horn and Johnson28, Corollary 7.8.2]),
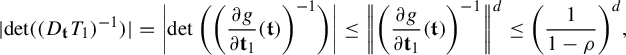 $$ \begin{align*} |\!\det((D_{\boldsymbol{\mathfrak{t}}}T_{1})^{-1})|= \bigg|\!\det\bigg( \bigg(\frac{\partial g}{{\partial\mathbf{t}_{1}}}(\boldsymbol{\mathfrak{t}} )\bigg)^{-1}\bigg)\bigg| \leq \bigg\|\bigg(\frac{\partial g}{{\partial\mathbf{t}_{1}}}(\boldsymbol{\mathfrak{t}} )\bigg)^{-1}\bigg\|^{d} \leq \bigg(\frac{1}{1-\rho}\bigg)^{d}, \end{align*} $$
$$ \begin{align*} |\!\det((D_{\boldsymbol{\mathfrak{t}}}T_{1})^{-1})|= \bigg|\!\det\bigg( \bigg(\frac{\partial g}{{\partial\mathbf{t}_{1}}}(\boldsymbol{\mathfrak{t}} )\bigg)^{-1}\bigg)\bigg| \leq \bigg\|\bigg(\frac{\partial g}{{\partial\mathbf{t}_{1}}}(\boldsymbol{\mathfrak{t}} )\bigg)^{-1}\bigg\|^{d} \leq \bigg(\frac{1}{1-\rho}\bigg)^{d}, \end{align*} $$
where the last inequality follows from Lemma 4.10. This completes the proof of (ii).
To shorten the notation, from now on we write
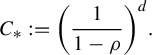 $$ \begin{align} C_{*}:=\bigg(\frac{1}{1-\rho}\bigg)^{d}. \end{align} $$
$$ \begin{align} C_{*}:=\bigg(\frac{1}{1-\rho}\bigg)^{d}. \end{align} $$
Let
![]() $\boldsymbol {\mathfrak {s}}=(\mathbf {s}_1,\ldots , \mathbf {s}_{\ell })\in \Delta $
and
$\boldsymbol {\mathfrak {s}}=(\mathbf {s}_1,\ldots , \mathbf {s}_{\ell })\in \Delta $
and
![]() $\delta , r>0$
. Let A be a given real invertible
$\delta , r>0$
. Let A be a given real invertible
![]() $d\times d$
matrix.
$d\times d$
matrix.
Write
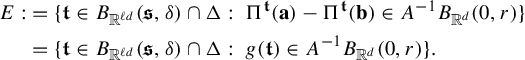 $$ \begin{align*} E:&=\{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}}, \delta)\cap \Delta:\; \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in A^{-1}B_{{\Bbb R}^d}(0,r)\} \\ &= \{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}}, \delta)\cap \Delta:\; g(\boldsymbol{\mathfrak{t}})\in A^{-1}B_{{\Bbb R}^d}(0,r)\}. \end{align*} $$
$$ \begin{align*} E:&=\{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}}, \delta)\cap \Delta:\; \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in A^{-1}B_{{\Bbb R}^d}(0,r)\} \\ &= \{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}}, \delta)\cap \Delta:\; g(\boldsymbol{\mathfrak{t}})\in A^{-1}B_{{\Bbb R}^d}(0,r)\}. \end{align*} $$
Below, we estimate
![]() $\mathcal L_{\ell d}(E)$
.
$\mathcal L_{\ell d}(E)$
.
Notice that
![]() $\mathcal L_{\ell d}(E)=\mathcal L_{\ell d}(T_{k^*}^{-1}(T_{k^*}(E)))$
. Recall that by Lemma 4.11, the mapping
$\mathcal L_{\ell d}(E)=\mathcal L_{\ell d}(T_{k^*}^{-1}(T_{k^*}(E)))$
. Recall that by Lemma 4.11, the mapping
![]() $T_{k^*}: \Delta \to {\Bbb R}^{\ell d}$
is injective and
$T_{k^*}: \Delta \to {\Bbb R}^{\ell d}$
is injective and
![]() $\det ((D_{\boldsymbol {\mathfrak {t}}}T_{k^*})^{-1})\leq C_*$
for
$\det ((D_{\boldsymbol {\mathfrak {t}}}T_{k^*})^{-1})\leq C_*$
for
![]() $\boldsymbol {\mathfrak {t}}\in \Delta $
. So by the substitution rule of multiple integration (see e.g. [Reference Rudin42, Theorem 10.9]),
$\boldsymbol {\mathfrak {t}}\in \Delta $
. So by the substitution rule of multiple integration (see e.g. [Reference Rudin42, Theorem 10.9]),
Next we estimate
![]() $\mathcal L_{\ell d}(T_{k^*}(E))$
. Without loss of generality, we may assume that
$\mathcal L_{\ell d}(T_{k^*}(E))$
. Without loss of generality, we may assume that
![]() $k^*=1$
. Notice that for each
$k^*=1$
. Notice that for each
![]() $\boldsymbol {\mathfrak {t}}\in E$
,
$\boldsymbol {\mathfrak {t}}\in E$
,
in the meantime, since
![]() $\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {a}),\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {b})\in S$
, it follows that
$\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {a}),\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {b})\in S$
, it follows that
Hence, for each
![]() $\boldsymbol {\mathfrak {t}}\in E$
,
$\boldsymbol {\mathfrak {t}}\in E$
,
Since
![]() $T_1(\boldsymbol {\mathfrak {t}})=(g(\boldsymbol {\mathfrak {t}}), \mathbf {t_2},\ldots , \mathbf {t}_{\ell })$
, it follows that
$T_1(\boldsymbol {\mathfrak {t}})=(g(\boldsymbol {\mathfrak {t}}), \mathbf {t_2},\ldots , \mathbf {t}_{\ell })$
, it follows that
where
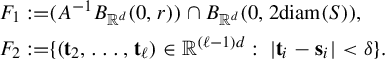 $$ \begin{align*} F_1:=&(A^{-1}B_{{\Bbb R}^d}(0,r))\cap B_{{\Bbb R}^d}(0, 2\mathrm{diam}(S)),\\ F_2:=&\{(\mathbf{t}_2,\ldots, \mathbf{t}_{\ell})\in {\Bbb R}^{(\ell-1)d}:\; |\mathbf{t}_i-\mathbf{s}_i|<\delta\}. \end{align*} $$
$$ \begin{align*} F_1:=&(A^{-1}B_{{\Bbb R}^d}(0,r))\cap B_{{\Bbb R}^d}(0, 2\mathrm{diam}(S)),\\ F_2:=&\{(\mathbf{t}_2,\ldots, \mathbf{t}_{\ell})\in {\Bbb R}^{(\ell-1)d}:\; |\mathbf{t}_i-\mathbf{s}_i|<\delta\}. \end{align*} $$
Consequently,
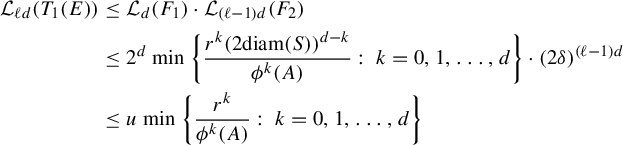 $$ \begin{align*} \mathcal L_{\ell d}(T_{1}(E))&\leq \mathcal L_{d}(F_1)\cdot \mathcal L_{(\ell-1)d}(F_2)\\ &\leq 2^d\min\bigg\{ \frac{r^k (2\mathrm{diam}(S))^{d-k}}{\phi^k(A)}:\; k=0,1,\ldots,d \bigg\}\cdot (2\delta)^{(\ell-1)d}\\ &\leq u \min\bigg\{ \frac{r^k }{\phi^k(A)}:\; k=0,1,\ldots,d \bigg\} \end{align*} $$
$$ \begin{align*} \mathcal L_{\ell d}(T_{1}(E))&\leq \mathcal L_{d}(F_1)\cdot \mathcal L_{(\ell-1)d}(F_2)\\ &\leq 2^d\min\bigg\{ \frac{r^k (2\mathrm{diam}(S))^{d-k}}{\phi^k(A)}:\; k=0,1,\ldots,d \bigg\}\cdot (2\delta)^{(\ell-1)d}\\ &\leq u \min\bigg\{ \frac{r^k }{\phi^k(A)}:\; k=0,1,\ldots,d \bigg\} \end{align*} $$
with
![]() $u:=2^{\ell d}\delta ^{(\ell -1)d}\max \{1, 2^d\mathrm {diam}(S)^d\}$
, where we have used Lemma 4.8 in the second inequality. Combining this with (4.37) yields that
$u:=2^{\ell d}\delta ^{(\ell -1)d}\max \{1, 2^d\mathrm {diam}(S)^d\}$
, where we have used Lemma 4.8 in the second inequality. Combining this with (4.37) yields that
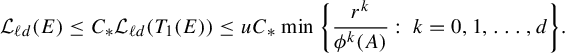 $$ \begin{align*}\mathcal L_{\ell d}(E)\leq C_* \mathcal L_{\ell d}(T_1(E))\leq uC_* \min\bigg\{ \frac{r^k }{\phi^k(A)}:\; k=0,1,\ldots,d \bigg\}. \end{align*} $$
$$ \begin{align*}\mathcal L_{\ell d}(E)\leq C_* \mathcal L_{\ell d}(T_1(E))\leq uC_* \min\bigg\{ \frac{r^k }{\phi^k(A)}:\; k=0,1,\ldots,d \bigg\}. \end{align*} $$
This completes the proof of Lemma 4.7.
5 Translational family of IFSs generated by a
 $C^1$
conformal IFS
$C^1$
conformal IFS
In this section, we prove the following result.
Theorem 5.1. Let
![]() $\mathcal F=\{f_i:\; S\to S\}_{i=1}^{\ell }$
be an IFS on a compact set
$\mathcal F=\{f_i:\; S\to S\}_{i=1}^{\ell }$
be an IFS on a compact set
![]() $S\subset {\Bbb R}^d$
. Suppose that the following properties hold.
$S\subset {\Bbb R}^d$
. Suppose that the following properties hold.
-
(i) The set S is connected,
 $S=\overline {\mathrm {int}(S)}$
and
$S=\overline {\mathrm {int}(S)}$
and
 $f_i(S)\subset \mathrm {int}(S)$
for all i.
$f_i(S)\subset \mathrm {int}(S)$
for all i. -
(ii) There is a bounded connected open set
 $U\supset S$
such that each
$U\supset S$
such that each
 $f_i$
extends to a
$f_i$
extends to a
 $C^1$
conformal diffeomorphism
$C^1$
conformal diffeomorphism
 $f_i:\; U\to f_i(U)\subset U$
with
$f_i:\; U\to f_i(U)\subset U$
with  $$ \begin{align*} \rho_i:=\sup_{x\in U}\|f_i'(x)\|<1. \end{align*} $$
$$ \begin{align*} \rho_i:=\sup_{x\in U}\|f_i'(x)\|<1. \end{align*} $$
-
(iii)
 $\max _{i\neq j} \rho _i+\rho _j<1$
.
$\max _{i\neq j} \rho _i+\rho _j<1$
.
Then there is a small
![]() $r_0>0$
such that the translational family
$r_0>0$
such that the translational family
![]() ${\mathcal F}^{\boldsymbol {\mathfrak {t}}}=\{f_i^{\boldsymbol {\mathfrak {t}}}=f_i+\mathbf {t}_i\}_{i=1}^{\ell }$
,
${\mathcal F}^{\boldsymbol {\mathfrak {t}}}=\{f_i^{\boldsymbol {\mathfrak {t}}}=f_i+\mathbf {t}_i\}_{i=1}^{\ell }$
,
![]() $\boldsymbol {\mathfrak {t}}=(\mathbf {t}_1,\ldots , \mathbf {t}_{\ell })\in \Delta :=\{\boldsymbol {\mathfrak {s}}\in {\Bbb R}^{\ell d}:\; |\boldsymbol {\mathfrak {s}}|<r_0\}$
, satisfies the GTC with respect to the Lebesgue measure
$\boldsymbol {\mathfrak {t}}=(\mathbf {t}_1,\ldots , \mathbf {t}_{\ell })\in \Delta :=\{\boldsymbol {\mathfrak {s}}\in {\Bbb R}^{\ell d}:\; |\boldsymbol {\mathfrak {s}}|<r_0\}$
, satisfies the GTC with respect to the Lebesgue measure
![]() $\mathcal L_{\ell d}$
on
$\mathcal L_{\ell d}$
on
![]() $\Delta $
.
$\Delta $
.
Proof By the assumptions (i) and (ii), we may pick two open connected sets V and W (for instance, we may let V and W be the
![]() $\epsilon $
-neighborhood and
$\epsilon $
-neighborhood and
![]() $2\epsilon $
-neighborhood of S, respectively, for a sufficiently small
$2\epsilon $
-neighborhood of S, respectively, for a sufficiently small
![]() $\epsilon>0$
), such that
$\epsilon>0$
), such that
Then by continuity, we can pick a small
![]() $r_0$
such that for all
$r_0$
such that for all
![]() $\boldsymbol {\mathfrak {t}}=(\mathbf {t}_1,\ldots , \mathbf {t}_{\ell })\in {\Bbb R}^{\ell d}$
with
$\boldsymbol {\mathfrak {t}}=(\mathbf {t}_1,\ldots , \mathbf {t}_{\ell })\in {\Bbb R}^{\ell d}$
with
![]() $|\boldsymbol {\mathfrak {t}}|<r_0$
,
$|\boldsymbol {\mathfrak {t}}|<r_0$
,
where
![]() $f_i^{\boldsymbol {\mathfrak {t}}}:=f_i+\mathbf {t}_i$
. Fix this
$f_i^{\boldsymbol {\mathfrak {t}}}:=f_i+\mathbf {t}_i$
. Fix this
![]() $r_0$
and set
$r_0$
and set
![]() $\Delta =\{\boldsymbol {\mathfrak {s}}\in {\Bbb R}^{\ell d}:\; |\boldsymbol {\mathfrak {s}}|<r_0\}$
. In what follows, we prove that the family
$\Delta =\{\boldsymbol {\mathfrak {s}}\in {\Bbb R}^{\ell d}:\; |\boldsymbol {\mathfrak {s}}|<r_0\}$
. In what follows, we prove that the family
![]() ${\mathcal F}^{\boldsymbol {\mathfrak {t}}}$
,
${\mathcal F}^{\boldsymbol {\mathfrak {t}}}$
,
![]() $\boldsymbol {\mathfrak {t}}\in \Delta $
, satisfies the GTC with respect to
$\boldsymbol {\mathfrak {t}}\in \Delta $
, satisfies the GTC with respect to
![]() $\mathcal L_{\ell d}$
on
$\mathcal L_{\ell d}$
on
![]() $\Delta $
.
$\Delta $
.
For
![]() $i=1,\ldots , \ell $
, define
$i=1,\ldots , \ell $
, define
![]() $g_i: \overline {W}\to {\Bbb R}$
by
$g_i: \overline {W}\to {\Bbb R}$
by
Then
![]() $g_i$
is continuous on
$g_i$
is continuous on
![]() $\overline {W}$
for each i. Define
$\overline {W}$
for each i. Define
![]() $\gamma :\; (0,\infty )\to (0,\infty )$
by
$\gamma :\; (0,\infty )\to (0,\infty )$
by
That is,
![]() $\gamma $
is a common continuity modulus of
$\gamma $
is a common continuity modulus of
![]() $g_1,\ldots , g_{\ell }$
. Clearly
$g_1,\ldots , g_{\ell }$
. Clearly
![]() $\lim _{u\to 0}\gamma (u)=0$
. Notice that for
$\lim _{u\to 0}\gamma (u)=0$
. Notice that for
![]() $\boldsymbol {\mathfrak {t}}\in \Delta $
,
$\boldsymbol {\mathfrak {t}}\in \Delta $
,
![]() $y\in W$
and
$y\in W$
and
![]() $\boldsymbol {\omega }\in \Sigma _n$
,
$\boldsymbol {\omega }\in \Sigma _n$
,
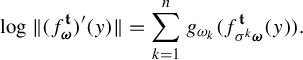 $$ \begin{align*}\log \|(f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )'(y)\|=\sum_{k=1}^n g_{\omega_k}(f^{\boldsymbol{\mathfrak{t}}}_{\sigma^k{\boldsymbol{\omega}}}(y)). \end{align*} $$
$$ \begin{align*}\log \|(f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )'(y)\|=\sum_{k=1}^n g_{\omega_k}(f^{\boldsymbol{\mathfrak{t}}}_{\sigma^k{\boldsymbol{\omega}}}(y)). \end{align*} $$
Using similar arguments (with minor changes) as in Step 1 and Step 2 of the proof of Proposition 4.3, we can show that the following two properties hold.
-
(a) Write for
 $n\in {\Bbb N}$
, (5.1)Then
$n\in {\Bbb N}$
, (5.1)Then $$ \begin{align} C_n:=\sup\bigg\{ \frac{\|(f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )'(y)\|}{\|(f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )'(z)\|}:\; \boldsymbol{\mathfrak{t}}\in \Delta,\; y,z\in W, \;{\boldsymbol{\omega}}\in \Sigma_n\bigg\}. \end{align} $$
$$ \begin{align} C_n:=\sup\bigg\{ \frac{\|(f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )'(y)\|}{\|(f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )'(z)\|}:\; \boldsymbol{\mathfrak{t}}\in \Delta,\; y,z\in W, \;{\boldsymbol{\omega}}\in \Sigma_n\bigg\}. \end{align} $$
 $\lim _{n\to \infty }({1}/{n})\log C_n=0$
.
$\lim _{n\to \infty }({1}/{n})\log C_n=0$
.
-
(b) For
 $y\in W$
,
$y\in W$
,
 $\boldsymbol {\mathfrak {s}},\boldsymbol {\mathfrak {t}}\in \Delta $
,
$\boldsymbol {\mathfrak {s}},\boldsymbol {\mathfrak {t}}\in \Delta $
,
 $n\in {\Bbb N}$
and
$n\in {\Bbb N}$
and
 ${\boldsymbol {\omega }}\in \Sigma _n$
, (5.2)where
${\boldsymbol {\omega }}\in \Sigma _n$
, (5.2)where $$ \begin{align} \frac{\|(f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )'(y)\|}{\|(f^{\boldsymbol{\mathfrak{s}}}_{{\boldsymbol{\omega}}} )'(y)\|}\leq \exp\bigg(n\gamma\bigg(\frac{|\boldsymbol{\mathfrak{t}}-\boldsymbol{\mathfrak{s}}|}{1-\theta}\bigg)\bigg), \end{align} $$
$$ \begin{align} \frac{\|(f^{\boldsymbol{\mathfrak{t}}}_{{\boldsymbol{\omega}}} )'(y)\|}{\|(f^{\boldsymbol{\mathfrak{s}}}_{{\boldsymbol{\omega}}} )'(y)\|}\leq \exp\bigg(n\gamma\bigg(\frac{|\boldsymbol{\mathfrak{t}}-\boldsymbol{\mathfrak{s}}|}{1-\theta}\bigg)\bigg), \end{align} $$
 $\theta :=\max _{1\leq i\leq \ell }\rho _i<1$
.
$\theta :=\max _{1\leq i\leq \ell }\rho _i<1$
.
Let
![]() $\mathcal H$
denote the collection of
$\mathcal H$
denote the collection of
![]() $C^1$
injective conformal mappings
$C^1$
injective conformal mappings
![]() $h: W\to W$
such that
$h: W\to W$
such that
![]() $h(\overline {V})\subset V$
. The following fact is known (for a proof, see e.g. part 3 of the proof of [Reference Patzschke39, Lemma 2.2]): there exists a constant
$h(\overline {V})\subset V$
. The following fact is known (for a proof, see e.g. part 3 of the proof of [Reference Patzschke39, Lemma 2.2]): there exists a constant
![]() $D\in (0,1)$
depending on V and W, such that
$D\in (0,1)$
depending on V and W, such that
Now fix
![]() $\boldsymbol {\mathfrak {s}}\in \Delta $
and
$\boldsymbol {\mathfrak {s}}\in \Delta $
and
![]() $\delta \in (0,r_0)$
. Let
$\delta \in (0,r_0)$
. Let
![]() $\mathbf {i},\mathbf {j}\in \Sigma $
with
$\mathbf {i},\mathbf {j}\in \Sigma $
with
![]() $\mathbf {i}\neq \mathbf {j}$
. Set
$\mathbf {i}\neq \mathbf {j}$
. Set
Write
![]() $\mathbf {a}=\sigma ^n \mathbf {i}$
and
$\mathbf {a}=\sigma ^n \mathbf {i}$
and
![]() $\mathbf {b}=\sigma ^n \mathbf {j}$
. Clearly
$\mathbf {b}=\sigma ^n \mathbf {j}$
. Clearly
![]() $a_1\neq b_1$
. Fix
$a_1\neq b_1$
. Fix
![]() $y\in S$
. We claim that for
$y\in S$
. We claim that for
![]() $r>0$
,
$r>0$
,
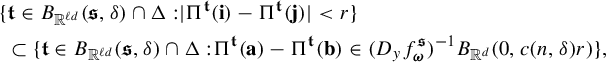 $$ \begin{align} &\{\boldsymbol{\mathfrak{t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\! |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{j})|< r\}\nonumber\\ &\text{}\; \subset \{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\! \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} B_{{\Bbb R}^d}(0,c(n,\delta)r) \}, \end{align} $$
$$ \begin{align} &\{\boldsymbol{\mathfrak{t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\! |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{j})|< r\}\nonumber\\ &\text{}\; \subset \{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\! \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} B_{{\Bbb R}^d}(0,c(n,\delta)r) \}, \end{align} $$
where
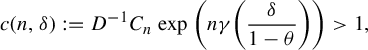 $$ \begin{align*}c(n,\delta):=D^{-1}C_n \exp\bigg(n\gamma\bigg(\frac{\delta}{1-\theta}\bigg)\bigg)>1, \end{align*} $$
$$ \begin{align*}c(n,\delta):=D^{-1}C_n \exp\bigg(n\gamma\bigg(\frac{\delta}{1-\theta}\bigg)\bigg)>1, \end{align*} $$
in which D is the constant from (5.3).
To show (5.4), let
![]() $\boldsymbol {\mathfrak {t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol {\mathfrak {s}},\delta )\cap \Delta $
so that
$\boldsymbol {\mathfrak {t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol {\mathfrak {s}},\delta )\cap \Delta $
so that
![]() $|\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {i})-\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {j})|<r$
. Notice that
$|\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {i})-\Pi ^{\boldsymbol {\mathfrak {t}}}(\mathbf {j})|<r$
. Notice that
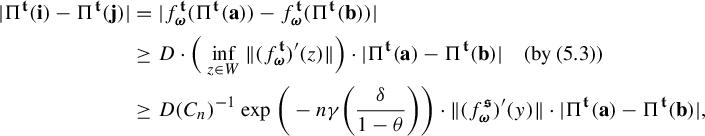 $$ \begin{align*} \begin{split} |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ j})|&=|f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}}(\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ a}))-f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}}(\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b}))|\\ &\geq D\cdot \Big(\inf_{z\in W}\| (f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}})'(z)\|\Big) \cdot |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})|\quad \text{(by (5.3))}\\ &\geq D(C_n)^{-1} \exp\bigg(-n\gamma\bigg(\frac{\delta}{1-\theta}\bigg)\bigg)\cdot\| (f^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})'(y)\|\cdot |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})|, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ j})|&=|f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}}(\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ a}))-f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}}(\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b}))|\\ &\geq D\cdot \Big(\inf_{z\in W}\| (f^{\boldsymbol{\mathfrak{t}}}_{\boldsymbol{\omega}})'(z)\|\Big) \cdot |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{ a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})|\quad \text{(by (5.3))}\\ &\geq D(C_n)^{-1} \exp\bigg(-n\gamma\bigg(\frac{\delta}{1-\theta}\bigg)\bigg)\cdot\| (f^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})'(y)\|\cdot |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})|, \end{split} \end{align*} $$
where, in the last inequality, we have used (5.1) and (5.2). It follows that
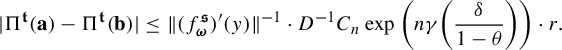 $$ \begin{align*}|\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})|\leq \| (f^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})'(y)\|^{-1}\cdot D^{-1}C_n \exp\bigg(n\gamma\bigg(\frac{\delta}{1-\theta}\bigg)\bigg)\cdot r. \end{align*} $$
$$ \begin{align*}|\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})|\leq \| (f^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})'(y)\|^{-1}\cdot D^{-1}C_n \exp\bigg(n\gamma\bigg(\frac{\delta}{1-\theta}\bigg)\bigg)\cdot r. \end{align*} $$
Since
![]() $(f^{\boldsymbol {\mathfrak {s}}}_{\boldsymbol {\omega }})'(y)=D_yf^{\boldsymbol {\mathfrak {s}}}_{\boldsymbol {\omega }}$
is a scalar multiple of an orthogonal matrix, the above inequality implies that
$(f^{\boldsymbol {\mathfrak {s}}}_{\boldsymbol {\omega }})'(y)=D_yf^{\boldsymbol {\mathfrak {s}}}_{\boldsymbol {\omega }}$
is a scalar multiple of an orthogonal matrix, the above inequality implies that
from which (5.4) follows.
By (5.4) and Lemma 4.7 (which is also valid in this context),
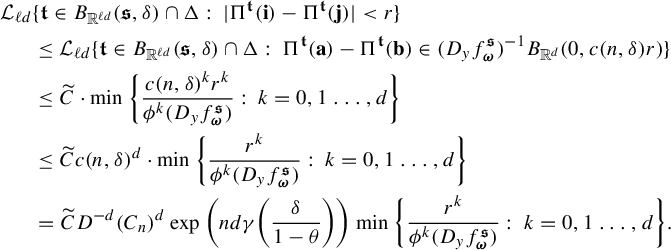 $$ \begin{align*} \begin{split} \mathcal L_{\ell d}&\{\boldsymbol{\mathfrak{t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{j})|< r\}\\ &\leq \mathcal L_{\ell d} \{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} B_{{\Bbb R}^d}(0,c(n,\delta)r) \}\\ &\leq \widetilde{C}\cdot\min\bigg\{\frac{c(n,\delta)^k r^k}{\phi^k(D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})}:\; k=0,1\ldots,d\bigg\}\\ &\leq \widetilde{C}c(n,\delta)^d\cdot\min\bigg\{\frac{ r^k}{\phi^k(D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})}:\; k=0,1\ldots,d\bigg\}\\ &= \widetilde{C}D^{-d} (C_n)^d \exp\bigg(nd\gamma\bigg(\frac{\delta}{1-\theta}\bigg)\bigg) \min\bigg\{\frac{r^k}{\phi^k(D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})}:\; k=0,1\ldots,d\bigg\}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \mathcal L_{\ell d}&\{\boldsymbol{\mathfrak{t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{j})|< r\}\\ &\leq \mathcal L_{\ell d} \{\boldsymbol{\mathfrak{t}}\in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; \Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{a})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{b})\in (D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})^{-1} B_{{\Bbb R}^d}(0,c(n,\delta)r) \}\\ &\leq \widetilde{C}\cdot\min\bigg\{\frac{c(n,\delta)^k r^k}{\phi^k(D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})}:\; k=0,1\ldots,d\bigg\}\\ &\leq \widetilde{C}c(n,\delta)^d\cdot\min\bigg\{\frac{ r^k}{\phi^k(D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})}:\; k=0,1\ldots,d\bigg\}\\ &= \widetilde{C}D^{-d} (C_n)^d \exp\bigg(nd\gamma\bigg(\frac{\delta}{1-\theta}\bigg)\bigg) \min\bigg\{\frac{r^k}{\phi^k(D_yf^{\boldsymbol{\mathfrak{s}}}_{\boldsymbol{\omega}})}:\; k=0,1\ldots,d\bigg\}. \end{split} \end{align*} $$
Since
![]() $y\in S$
is arbitrary and
$y\in S$
is arbitrary and
![]() $\Pi ^{\boldsymbol {\mathfrak {s}}}(\Sigma )\subset S$
, recalling
$\Pi ^{\boldsymbol {\mathfrak {s}}}(\Sigma )\subset S$
, recalling
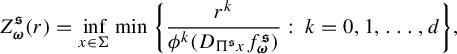 $$ \begin{align*} Z_{{\boldsymbol{\omega}}}^{\boldsymbol{\mathfrak{s}}}(r)= \inf_{x\in \Sigma} \min\bigg \{ \frac{r^k}{ \phi^k (D_{\Pi^{\boldsymbol{\mathfrak{s}}} x}f^{\boldsymbol{\mathfrak{s}}}_{{\boldsymbol{\omega}}} ) }:\; k=0, 1,\ldots, d\bigg\}, \end{align*} $$
$$ \begin{align*} Z_{{\boldsymbol{\omega}}}^{\boldsymbol{\mathfrak{s}}}(r)= \inf_{x\in \Sigma} \min\bigg \{ \frac{r^k}{ \phi^k (D_{\Pi^{\boldsymbol{\mathfrak{s}}} x}f^{\boldsymbol{\mathfrak{s}}}_{{\boldsymbol{\omega}}} ) }:\; k=0, 1,\ldots, d\bigg\}, \end{align*} $$
it follows that
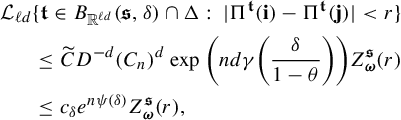 $$ \begin{align*} \mathcal L_{\ell d}& \{\boldsymbol{\mathfrak{t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{j})|< r\} \\ & \leq \widetilde{C}D^{-d} (C_n)^d \exp\bigg(nd\gamma\bigg(\frac{\delta}{1-\theta}\bigg)\bigg)Z_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}}(r)\\ &\leq c_{\delta} e^{n\psi(\delta)}Z_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}}(r), \end{align*} $$
$$ \begin{align*} \mathcal L_{\ell d}& \{\boldsymbol{\mathfrak{t}} \in B_{{\Bbb R}^{\ell d}}(\boldsymbol{\mathfrak{s}},\delta)\cap \Delta:\; |\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{i})-\Pi^{\boldsymbol{\mathfrak{t}}}(\mathbf{j})|< r\} \\ & \leq \widetilde{C}D^{-d} (C_n)^d \exp\bigg(nd\gamma\bigg(\frac{\delta}{1-\theta}\bigg)\bigg)Z_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}}(r)\\ &\leq c_{\delta} e^{n\psi(\delta)}Z_{\boldsymbol{\omega}}^{\boldsymbol{\mathfrak{s}}}(r), \end{align*} $$
where
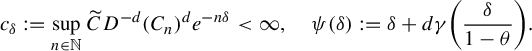 $$ \begin{align*}c_{\delta}:= \sup_{n\in {\Bbb N}}\widetilde{C}D^{-d} (C_n)^d e^{-n\delta}<\infty,\quad \psi(\delta):=\delta+d\gamma\bigg(\frac{\delta}{1-\theta}\bigg). \end{align*} $$
$$ \begin{align*}c_{\delta}:= \sup_{n\in {\Bbb N}}\widetilde{C}D^{-d} (C_n)^d e^{-n\delta}<\infty,\quad \psi(\delta):=\delta+d\gamma\bigg(\frac{\delta}{1-\theta}\bigg). \end{align*} $$
Since
![]() $\lim _{u\to 0}\gamma (u)=0$
, we see that
$\lim _{u\to 0}\gamma (u)=0$
, we see that
![]() $\lim _{\delta \to 0} \psi (\delta )=0$
. Thus,
$\lim _{\delta \to 0} \psi (\delta )=0$
. Thus,
![]() $({\mathcal F}^{\boldsymbol {\mathfrak {t}}})_{\boldsymbol {\mathfrak {t}}\in \Delta }$
satisfies the GTC.
$({\mathcal F}^{\boldsymbol {\mathfrak {t}}})_{\boldsymbol {\mathfrak {t}}\in \Delta }$
satisfies the GTC.
6 Direct product of parameterized families of
 $C^1$
IFSs
$C^1$
IFSs
In this section, we study the direct product of parameterized families of
![]() $C^1$
IFSs (cf. Definition 1.5). The main result is the following, stating that the property of the GTC is preserved under the direct product.
$C^1$
IFSs (cf. Definition 1.5). The main result is the following, stating that the property of the GTC is preserved under the direct product.
Proposition 6.1. Let
![]() $\ell \in {\Bbb N}$
with
$\ell \in {\Bbb N}$
with
![]() $\ell \geq 2$
. Suppose that for
$\ell \geq 2$
. Suppose that for
![]() $k=1,\ldots , n$
,
$k=1,\ldots , n$
,
![]() $(\mathcal F_k^{t_k})_{t_k\in {\Omega }_k}$
is a parameterized family of
$(\mathcal F_k^{t_k})_{t_k\in {\Omega }_k}$
is a parameterized family of
![]() $C^1$
IFSs on
$C^1$
IFSs on
![]() $Z_j\subset {\Bbb R}^{q_k}$
, satisfying the GTC with respect to a locally finite Borel measure
$Z_j\subset {\Bbb R}^{q_k}$
, satisfying the GTC with respect to a locally finite Borel measure
![]() $\eta _k$
on the metric space
$\eta _k$
on the metric space
![]() $({\Omega }_k, d_{{\Omega }_k})$
. Moreover, suppose all the individual IFSs have
$({\Omega }_k, d_{{\Omega }_k})$
. Moreover, suppose all the individual IFSs have
![]() $\ell $
contractions. Set
$\ell $
contractions. Set
Endow
![]() ${\Omega }:={\Omega }_1\times \cdots \times {\Omega }_n$
with the product metric
${\Omega }:={\Omega }_1\times \cdots \times {\Omega }_n$
with the product metric
![]() $d_{\Omega }$
as follows:
$d_{\Omega }$
as follows:
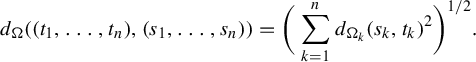 $$ \begin{align*}d_{\Omega}((t_1,\ldots, t_n), (s_1,\ldots, s_n))=\bigg(\sum_{k=1}^n d_{{\Omega}_k}(s_k, t_k)^2\bigg)^{1/2}. \end{align*} $$
$$ \begin{align*}d_{\Omega}((t_1,\ldots, t_n), (s_1,\ldots, s_n))=\bigg(\sum_{k=1}^n d_{{\Omega}_k}(s_k, t_k)^2\bigg)^{1/2}. \end{align*} $$
Then the family
![]() $\mathcal F^{(t_1,\ldots , t_n)}$
,
$\mathcal F^{(t_1,\ldots , t_n)}$
,
![]() $(t_1,\ldots , t_n)\in {\Omega }_1\times \cdots \times {\Omega }_n$
, satisfies the GTC with respect to
$(t_1,\ldots , t_n)\in {\Omega }_1\times \cdots \times {\Omega }_n$
, satisfies the GTC with respect to
![]() $\eta _1\times \cdots \times \eta _n$
.
$\eta _1\times \cdots \times \eta _n$
.
To prove the above proposition, we need the following.
Lemma 6.2.
-
(i) Let A be a real non-singular
 $d\times d$
matrix with singular values
$d\times d$
matrix with singular values
 $\alpha _1\geq \cdots \geq \alpha _d$
. Then for each
$\alpha _1\geq \cdots \geq \alpha _d$
. Then for each
 $r>0$
, where
$r>0$
, where $$ \begin{align*}\min\bigg\{\frac{r^p}{\phi^p(A)}:\; p=0,1,\ldots,d\bigg\}=\prod_{i=1}^d\frac{\min\{ \alpha_i, r\}}{\alpha_i}, \end{align*} $$
$$ \begin{align*}\min\bigg\{\frac{r^p}{\phi^p(A)}:\; p=0,1,\ldots,d\bigg\}=\prod_{i=1}^d\frac{\min\{ \alpha_i, r\}}{\alpha_i}, \end{align*} $$
 $\phi ^s(\cdot )$
is the singular value function defined as in (2.5).
$\phi ^s(\cdot )$
is the singular value function defined as in (2.5).
-
(ii) For
 $j=1,\ldots , n$
, let
$j=1,\ldots , n$
, let
 $A_j$
be a real non-singular
$A_j$
be a real non-singular
 $d_j\times d_j$
matrix. Set Then
$d_j\times d_j$
matrix. Set Then $$ \begin{align*}M=\mathrm{diag}(A_1,\ldots, A_n):=\left[ \begin{array}{cccc} A_1 & {\textbf{0}} & \cdots & {\textbf{0}}\\ {\textbf{0}} & A_2 & \cdots & {\textbf{0}}\\ \vdots & \vdots &\ddots & {\textbf{0}}\\ {\textbf{0}} & {\textbf{0}} & \cdots & A_n \end{array} \right]. \end{align*} $$
(6.1)
$$ \begin{align*}M=\mathrm{diag}(A_1,\ldots, A_n):=\left[ \begin{array}{cccc} A_1 & {\textbf{0}} & \cdots & {\textbf{0}}\\ {\textbf{0}} & A_2 & \cdots & {\textbf{0}}\\ \vdots & \vdots &\ddots & {\textbf{0}}\\ {\textbf{0}} & {\textbf{0}} & \cdots & A_n \end{array} \right]. \end{align*} $$
(6.1) $$ \begin{align} \min&\bigg\{\frac{r^p}{\phi^p(M)}:\! p=0,1,\ldots,d_1+\cdots+d_n\bigg\}\nonumber\\ &=\prod_{i=1}^n \min\bigg\{\frac{r^p}{\phi^p(A_i)}:\! p=0,1,\ldots,d_i\bigg\}. \end{align} $$
$$ \begin{align} \min&\bigg\{\frac{r^p}{\phi^p(M)}:\! p=0,1,\ldots,d_1+\cdots+d_n\bigg\}\nonumber\\ &=\prod_{i=1}^n \min\bigg\{\frac{r^p}{\phi^p(A_i)}:\! p=0,1,\ldots,d_i\bigg\}. \end{align} $$
Proof The proof of (i) is direct and simple. We leave it to the reader as an exercise. Part (ii) is just a consequence of (i), using the fact that the set of singular values (including the multiplicity) of M are precisely the union of those of
![]() $A_i$
,
$A_i$
,
![]() $i=1,\ldots , n$
.
$i=1,\ldots , n$
.
Now we are ready to prove Proposition 6.1.
Proof of Proposition 6.1 Write
For
![]() $\boldsymbol {\omega }=\omega _1\ldots \omega _m\in \Sigma _*$
, write
$\boldsymbol {\omega }=\omega _1\ldots \omega _m\in \Sigma _*$
, write
![]() $f_{{\boldsymbol {\omega }},k}^{t_k}=f_{\omega _1,k}^{t_k}\circ \cdots \circ f_{\omega _m,k}^{t_k}$
. Let
$f_{{\boldsymbol {\omega }},k}^{t_k}=f_{\omega _1,k}^{t_k}\circ \cdots \circ f_{\omega _m,k}^{t_k}$
. Let
![]() $\Pi ^{t_k}_k$
denote the coding map associated with the IFS
$\Pi ^{t_k}_k$
denote the coding map associated with the IFS
![]() $\mathcal F_k^{t_k}$
, and
$\mathcal F_k^{t_k}$
, and
![]() $\Pi ^{(t_1,\ldots , t_n)}$
the coding map associated with the IFS
$\Pi ^{(t_1,\ldots , t_n)}$
the coding map associated with the IFS
![]() $\mathcal F^{(t_1,\ldots , t_n)}$
. According to the GTC assumption on the families
$\mathcal F^{(t_1,\ldots , t_n)}$
. According to the GTC assumption on the families
![]() $(\mathcal F_k^{t_k})_{t_k\in {\Omega }_k}$
,
$(\mathcal F_k^{t_k})_{t_k\in {\Omega }_k}$
,
![]() $k=1,\ldots , n$
, there exist
$k=1,\ldots , n$
, there exist
![]() $\delta _0>0$
and a function
$\delta _0>0$
and a function
![]() $\psi :\; (0, \delta _0)\to [0,\infty )$
with
$\psi :\; (0, \delta _0)\to [0,\infty )$
with
![]() $\lim _{\delta \to 0}\psi (\delta )=0$
such that for every
$\lim _{\delta \to 0}\psi (\delta )=0$
such that for every
![]() $\delta \kern1.5pt{\in}\kern1.5pt (0, \delta _0)$
and
$\delta \kern1.5pt{\in}\kern1.5pt (0, \delta _0)$
and
![]() $(s_1,\ldots , s_n)\kern1.5pt{\in}\kern1.5pt {\Omega }_1\times \cdots \times {\Omega }_n$
, there is
$(s_1,\ldots , s_n)\kern1.5pt{\in}\kern1.5pt {\Omega }_1\times \cdots \times {\Omega }_n$
, there is
![]() $C\kern1.5pt{=}\kern1.5pt C(\delta ,s_1,\ldots , s_n)\kern1.5pt{>}\kern1.5pt 0$
satisfying the following: for each
$C\kern1.5pt{=}\kern1.5pt C(\delta ,s_1,\ldots , s_n)\kern1.5pt{>}\kern1.5pt 0$
satisfying the following: for each
![]() $k\in \{1,\ldots , n\}$
, distinct
$k\in \{1,\ldots , n\}$
, distinct
![]() $\mathbf {i},\mathbf { j}\in \Sigma $
and
$\mathbf {i},\mathbf { j}\in \Sigma $
and
![]() $r>0$
,
$r>0$
,
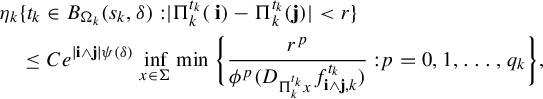 $$ \begin{align} \eta_k&\{t_k\in B_{{\Omega}_k}(s_k, \delta):\! |\Pi^{t_k}_k({\textbf{ i}})-\Pi^{t_k}_k({\textbf{j}}) |< r\}\nonumber\\ &\leq C e^{|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)} \inf_{x\in \Sigma} \min\bigg\{ \frac{r^p}{\phi^p(D_{\Pi^{t_k}_kx}f_{\mathbf{i}\wedge \mathbf{j}, k}^{t_k})}:\! p=0,1,\ldots, q_k \bigg\}, \end{align} $$
$$ \begin{align} \eta_k&\{t_k\in B_{{\Omega}_k}(s_k, \delta):\! |\Pi^{t_k}_k({\textbf{ i}})-\Pi^{t_k}_k({\textbf{j}}) |< r\}\nonumber\\ &\leq C e^{|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)} \inf_{x\in \Sigma} \min\bigg\{ \frac{r^p}{\phi^p(D_{\Pi^{t_k}_kx}f_{\mathbf{i}\wedge \mathbf{j}, k}^{t_k})}:\! p=0,1,\ldots, q_k \bigg\}, \end{align} $$
where
![]() $B_{{\Omega }_k}(s_k, \delta )$
stands for the closed ball in
$B_{{\Omega }_k}(s_k, \delta )$
stands for the closed ball in
![]() ${\Omega }_k$
of radius
${\Omega }_k$
of radius
![]() $\delta $
centered at
$\delta $
centered at
![]() $s_k$
. Writing
$s_k$
. Writing
![]() $\mathbf {t}=(t_1,\ldots , t_n)$
,
$\mathbf {t}=(t_1,\ldots , t_n)$
,
![]() $\mathbf {s}=(s_1,\ldots , s_n)$
and using (6.2),
$\mathbf {s}=(s_1,\ldots , s_n)$
and using (6.2),
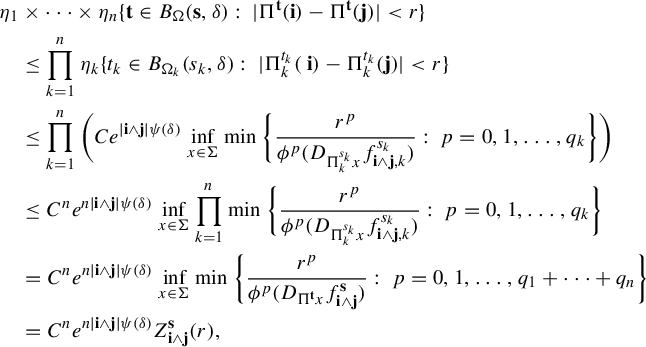 $$ \begin{align*} \eta_1&\times \cdots\times \eta_n\{ \mathbf{t}\in B_{{\Omega}}(\mathbf{s}, \delta): \; |\Pi^{\mathbf{t}}({\textbf{i}})-\Pi^{\mathbf{t}}({\textbf{j}}) |< r\}\\ &\leq \prod_{k=1}^n\eta_k\{t_k\in B_{{\Omega}_k}(s_k, \delta): \; |\Pi^{t_k}_k({\textbf{ i}})-\Pi^{t_k}_k({\textbf{j}}) |< r\}\\ &\leq \prod_{k=1}^n \bigg(C e^{|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)} \inf_{x\in \Sigma} \min\bigg\{ \frac{r^p}{\phi^p(D_{\Pi^{s_k}_kx}f_{\mathbf{i}\wedge \mathbf{j}, k}^{s_k})}:\; p=0,1,\ldots, q_k \bigg\}\bigg)\\ & \leq C^n e^{n|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)}\inf_{x\in \Sigma}\prod_{k=1}^n \min\bigg\{ \frac{r^p}{\phi^p(D_{\Pi^{s_k}_kx}f_{\mathbf{i}\wedge \mathbf{j}, k}^{s_k})}:\; p=0,1,\ldots, q_k \bigg\}\\ & =C^n e^{n|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)}\inf_{x\in \Sigma}\min \bigg\{ \frac{r^p}{\phi^p(D_{\Pi^{\mathbf{t}}x}f_{\mathbf{i}\wedge \mathbf{j}}^{\mathbf{s}})}:\; p=0,1,\ldots, q_1+\cdots+q_n \bigg\}\\ & =C^n e^{n|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)}Z_{\mathbf{i}\wedge\mathbf{j}}^{\mathbf{s}}(r), \end{align*} $$
$$ \begin{align*} \eta_1&\times \cdots\times \eta_n\{ \mathbf{t}\in B_{{\Omega}}(\mathbf{s}, \delta): \; |\Pi^{\mathbf{t}}({\textbf{i}})-\Pi^{\mathbf{t}}({\textbf{j}}) |< r\}\\ &\leq \prod_{k=1}^n\eta_k\{t_k\in B_{{\Omega}_k}(s_k, \delta): \; |\Pi^{t_k}_k({\textbf{ i}})-\Pi^{t_k}_k({\textbf{j}}) |< r\}\\ &\leq \prod_{k=1}^n \bigg(C e^{|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)} \inf_{x\in \Sigma} \min\bigg\{ \frac{r^p}{\phi^p(D_{\Pi^{s_k}_kx}f_{\mathbf{i}\wedge \mathbf{j}, k}^{s_k})}:\; p=0,1,\ldots, q_k \bigg\}\bigg)\\ & \leq C^n e^{n|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)}\inf_{x\in \Sigma}\prod_{k=1}^n \min\bigg\{ \frac{r^p}{\phi^p(D_{\Pi^{s_k}_kx}f_{\mathbf{i}\wedge \mathbf{j}, k}^{s_k})}:\; p=0,1,\ldots, q_k \bigg\}\\ & =C^n e^{n|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)}\inf_{x\in \Sigma}\min \bigg\{ \frac{r^p}{\phi^p(D_{\Pi^{\mathbf{t}}x}f_{\mathbf{i}\wedge \mathbf{j}}^{\mathbf{s}})}:\; p=0,1,\ldots, q_1+\cdots+q_n \bigg\}\\ & =C^n e^{n|{\textbf{i}}\wedge {\textbf{j}}| \psi(\delta)}Z_{\mathbf{i}\wedge\mathbf{j}}^{\mathbf{s}}(r), \end{align*} $$
where we have used (6.1) in the second last equality. Hence, the family
![]() $\mathcal F^{\mathbf {t}}$
,
$\mathcal F^{\mathbf {t}}$
,
![]() $\mathbf {t}\in {\Omega }$
, satisfies the GTC with respect to the measure
$\mathbf {t}\in {\Omega }$
, satisfies the GTC with respect to the measure
![]() $\eta _1\times \cdots \times \eta _n$
, where the involved constant and the function in the definition of the GTC are
$\eta _1\times \cdots \times \eta _n$
, where the involved constant and the function in the definition of the GTC are
![]() $C^n$
and
$C^n$
and
![]() $n\psi (\cdot )$
, respectively.
$n\psi (\cdot )$
, respectively.
7 The proof of Theorem 1.6 and final questions
Now we are ready to prove Theorem 1.6.
Below we list a few ‘folklore’ open questions on the dimension of the attractors of
![]() $C^1$
IFSs. One may formulate the corresponding questions on the dimension of push-forwards of ergodic invariant measures on the attractors.
$C^1$
IFSs. One may formulate the corresponding questions on the dimension of push-forwards of ergodic invariant measures on the attractors.
Question 7.1. Is it true that for every
![]() $C^1$
IFS
$C^1$
IFS
![]() $\mathcal F=\{f_i\}_{i=1}^{\ell }$
on
$\mathcal F=\{f_i\}_{i=1}^{\ell }$
on
![]() ${\Bbb R}^d$
satisfying (1.8), there is a neighborhood
${\Bbb R}^d$
satisfying (1.8), there is a neighborhood
![]() $\Delta $
of
$\Delta $
of
![]() ${\textbf {0}}$
in
${\textbf {0}}$
in
![]() ${\Bbb R}^{\ell d}$
such that for
${\Bbb R}^{\ell d}$
such that for
![]() $\mathcal L_{\ell d}$
-a.e.
$\mathcal L_{\ell d}$
-a.e.
![]() $\boldsymbol {\mathfrak {t}}=({\textbf {t}}_1,\ldots , {\textbf {t}}_{\ell })\in \Delta $
,
$\boldsymbol {\mathfrak {t}}=({\textbf {t}}_1,\ldots , {\textbf {t}}_{\ell })\in \Delta $
,
where
![]() $K^{\boldsymbol {\mathfrak {t}}}$
is the attractor of the IFS
$K^{\boldsymbol {\mathfrak {t}}}$
is the attractor of the IFS
![]() ${\mathcal F}^{\boldsymbol {\mathfrak {t}}}=\{f_i+{\textbf {t}}_{i}\}_{i=1}^{\ell }$
?
${\mathcal F}^{\boldsymbol {\mathfrak {t}}}=\{f_i+{\textbf {t}}_{i}\}_{i=1}^{\ell }$
?
Question 7.2. Do we have
for the attractor K of a ‘generic’
![]() $C^1$
IFS
$C^1$
IFS
![]() $\mathcal F$
on
$\mathcal F$
on
![]() ${\Bbb R}^d$
(in an appropriate sense)?
${\Bbb R}^d$
(in an appropriate sense)?
Acknowledgements
The authors would like to thank the referee for helpful comments and suggestions. They also thank Zhou Feng for catching some typos. The research of D.-J.F. was partially supported by a HKRGC GRF grant and the Direct Grant for Research in CUHK. The research of K.S. was partially supported by the grant OTKA K104745. A significant part of the research was done during the visit of K.S. to CUHK, which was supported by a HKRGC GRF grant.