Published online by Cambridge University Press: 18 June 2021
We prove that in every compact space of Delone sets in 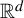 ${\mathbb {R}}^d$
, which is minimal with respect to the action by translations, either all Delone sets are uniformly spread or continuously many distinct bounded displacement equivalence classes are represented, none of which contains a lattice. The implied limits are taken with respect to the Chabauty–Fell topology, which is the natural topology on the space of closed subsets of
${\mathbb {R}}^d$
, which is minimal with respect to the action by translations, either all Delone sets are uniformly spread or continuously many distinct bounded displacement equivalence classes are represented, none of which contains a lattice. The implied limits are taken with respect to the Chabauty–Fell topology, which is the natural topology on the space of closed subsets of 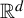 ${\mathbb {R}}^d$
. This topology coincides with the standard local topology in the finite local complexity setting, and it follows that the dichotomy holds for all minimal spaces of Delone sets associated with well-studied constructions such as cut-and-project sets and substitution tilings, whether or not finite local complexity is assumed.
${\mathbb {R}}^d$
. This topology coincides with the standard local topology in the finite local complexity setting, and it follows that the dichotomy holds for all minimal spaces of Delone sets associated with well-studied constructions such as cut-and-project sets and substitution tilings, whether or not finite local complexity is assumed.