Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T03:54:13.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Volume hyperbolicity and wildness

Published online by Cambridge University Press:  19 September 2016

CHRISTIAN BONATTI  and
KATSUTOSHI SHINOHARA
CHRISTIAN BONATTI
Affiliation:
Institut de Mathématiques de Bourgogne, UMR 5584, CNRS, Université de Bourgogne, Dijon 21004, France email [email protected]
KATSUTOSHI SHINOHARA
Affiliation:
Graduate School of Commerce and Management, Hitotsubashi University, 2-1 Naka, Kunitachi, Tokyo, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is known that volume hyperbolicity (partial hyperbolicity and uniform expansion or contraction of the volume in the extremal bundles) is a necessary condition for robust transitivity or robust chain recurrence and hence for tameness. In this paper, on any $3$-manifold we build examples of quasi-attractors which are volume hyperbolic and wild at the same time. As a main corollary, we see that, for any closed $3$-manifold 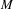$M$, the space 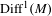$\text{Diff}^{1}(M)$ admits a non-empty open set where every 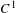$C^{1}$-generic diffeomorphism has no attractors or repellers. The main tool of our construction is the notion of flexible periodic points introduced in the authors’ previous paper. In order to eject the flexible points from the quasi-attractor, we control the topology of the quasi-attractor using the notion of partially hyperbolic filtrating Markov partitions, which we introduce in this paper.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 3 , May 2018 , pp. 886 - 920
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdenur, F.. Generic robustness of spectral decompositions. Ann. Sci. Éc. Norm. Supér. (4) 36(2) (2003), 213–224.Google Scholar
Abdenur, F., Bonatti, C., Crovisier, S., Díaz, L. J. and Wen, L.. Periodic points and homoclinic classes. Ergod. Th. & Dynam. Sys. 27(1) (2007), 1–22.Google Scholar
Bonatti, C.. Towards a global view of dynamical systems, for the C 1 -topology. Ergod. Th. & Dynam. Sys. 31(4) (2011), 959–993.Google Scholar
Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158(1) (2004), 33–104.Google Scholar
Bonatti, C. and Crovisier, S.. Center manifolds for partially hyperbolic sets without strong unstable connections. J. Inst. Math. Jussieu, published online 11 March 2015, doi:10.1017/S1474748015000055.Google Scholar
Bonatti, C. and Díaz, L. J.. Persistent nonhyperbolic transitive diffeomorphisms. Ann. of Math. (2) 143(2) (1996), 357–396.Google Scholar
Bonatti, C. and Díaz, L. J.. Connexions hétéroclines et généricité d’une infinité de puits et de sources. Ann. Sci. Éc. Norm. Supér. (4) 32(1) (1999), 135–150.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L. J.. On maximal transitive sets of generic diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 96 (2003), 171–197.Google Scholar
Bonatti, C., Díaz, L. J. and Kiriki, S.. Stabilization of heterodimensional cycles. Nonlinearity 25(4) (2012), 931–960.Google Scholar
Bonatti, C., Díaz, L. J. and Pujals, E.. A C 1 -generic dichotomy for diffeomorphisms: weak forms of hyperbolicity or infinitely many sinks or sources. Ann. of Math. (2) 158(2) (2003), 355–418.Google Scholar
Bonatti, C., Díaz, L. J. and Viana, M.. Dynamics beyond uniform hyperbolicity. A global geometric and probabilistic perspective. Encyclopaedia of Mathematical Sciences (Mathematical Physics, III, 102) . Springer, Berlin, 2005.Google Scholar
Bonatti, C., Li, M. and Yang, D.. On the existence of attractors. Trans. Amer. Math. Soc. 365 (2013), 1369–1391.Google Scholar
Bonatti, C. and Shinohara, K.. Flexible periodic points. Ergod. Th. & Dynam. Sys. 36(5) (2015), 1394–1422.Google Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115 (2000), 157–193.Google Scholar
Carvalho, M.. Sinai–Ruelle–Bowen measures for n-dimensional derived from Anosov diffeomorphisms. Ergod. Th. & Dynam. Sys. 13(01) (1993), 21–44.Google Scholar
Crovisier, S. and Pujals, E.. Essential hyperbolicity and homoclinic bifurcations: a dichotomy phenomenon/mechanism for diffeomorphisms. Invent. Math. 201(2) (2015), 385–517.Google Scholar
Gibbons, J. C.. One-dimensional basic sets in the three-sphere. Trans. Amer. Math. Soc. 164 (1972), 163–178.CrossRefGoogle Scholar
Gourmelon, N.. Adapted metrics for dominated splittings. Ergod. Th. & Dynam. Sys. 27(6) (2007), 1839–1849.Google Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583) . Springer, New York, 1977.Google Scholar
Mañé, R.. Contributions to the stability conjecture. Topology 17(4) (1978), 383–396.Google Scholar
Shub, M.. Topologically transitive diffeomorphisms of T 4 . Proc. Sympos. Differential Equations and Dynamical Systems (Lecture Notes in Mathematics, 206) . Springer, Berlin, 1971, pp. 39–40.Google Scholar
Williams, R.. One-dimensional non-wandering sets. Topology 6 (1967), 473–487.Google Scholar