Universal curves in the center problem for Abel differential equations

Abstract

We study the center problem for the class 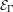${\mathcal{E}}_{{\rm\Gamma}}$ of Abel differential equations 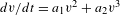$dv/dt=a_{1}v^{2}+a_{2}v^{3}$, 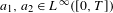$a_{1},a_{2}\in L^{\infty }([0,T])$, such that images of Lipschitz paths 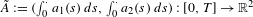$\tilde{A}:=(\int _{0}^{\cdot }a_{1}(s)\,ds,\int _{0}^{\cdot }a_{2}(s)\,ds):[0,T]\rightarrow \mathbb{R}^{2}$ belong to a fixed compact rectifiable curve ${\rm\Gamma}$. Such a curve is said to be universal if whenever an equation in 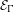${\mathcal{E}}_{{\rm\Gamma}}$ has center on 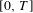$[0,T]$, this center must be universal, i.e. all iterated integrals in coefficients 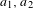$a_{1},a_{2}$ of this equation must vanish. We investigate some basic properties of universal curves. Our main results include an algebraic description of a universal curve in terms of a certain homomorphism of its fundamental group into the group of locally convergent invertible power series with the product being the composition of series, explicit examples of universal curves, and approximation of Lipschitz triangulable curves by universal ones.