Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Oprocha, Piotr
2014.
TRANSITIVITY, TWO-SIDED LIMIT SHADOWING PROPERTY AND DENSE ω-CHAOS.
Journal of the Korean Mathematical Society,
Vol. 51,
Issue. 4,
p.
837.
Drwiega, T.
and
Oprocha, P.
2014.
Topologically Mixing Maps and the Pseudoarc.
Ukrainian Mathematical Journal,
Vol. 66,
Issue. 2,
p.
197.
Bartoll, Salud
Martínez-Giménez, Félix
and
Peris, Alfredo
2016.
Operators with the specification property.
Journal of Mathematical Analysis and Applications,
Vol. 436,
Issue. 1,
p.
478.
ACOSTA, GERARDO
HERNÁNDEZ-GUTIÉRREZ, RODRIGO
NAGHMOUCHI, ISSAM
and
OPROCHA, PIOTR
2017.
Periodic points and transitivity on dendrites.
Ergodic Theory and Dynamical Systems,
Vol. 37,
Issue. 7,
p.
2017.
LI, JIAN
and
OPROCHA, PIOTR
2018.
Properties of invariant measures in dynamical systems with the shadowing property.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 6,
p.
2257.
Foryś-Krawiec, Magdalena
Hantáková, Jana
and
Oprocha, Piotr
2022.
On the structure of $ \alpha $-limit sets of backward trajectories for graph maps.
Discrete & Continuous Dynamical Systems,
Vol. 42,
Issue. 3,
p.
1435.
Banerjee, Kuntal
Bhattacharyya, Anubrato
and
Mondal, Subhamoy
2024.
Total Variation of a Curve Under Chaos on the Real Line and on a Finite Graph.
Qualitative Theory of Dynamical Systems,
Vol. 23,
Issue. 1,
Bobok, Jozef
Činč, Jernej
Oprocha, Piotr
and
Troubetzkoy, Serge
2024.
Are generic dynamical properties stable under composition with rotations?.
Proceedings of the American Mathematical Society,
Bobok, Jozef
Činč, Jernej
Oprocha, Piotr
and
Troubetzkoy, Serge
2025.
Continuous Lebesgue measure-preserving maps on one-dimensional manifolds: A survey.
Topology and its Applications,
Vol. 364,
Issue. ,
p.
109101.
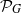 ${ \mathcal{P} }_{G} $ be the family of all topologically mixing, but not exact self-maps of a topological graph
${ \mathcal{P} }_{G} $ be the family of all topologically mixing, but not exact self-maps of a topological graph 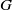 $G$. It is proved that the infimum of topological entropies of maps from
$G$. It is proved that the infimum of topological entropies of maps from 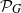 ${ \mathcal{P} }_{G} $ is bounded from below by
${ \mathcal{P} }_{G} $ is bounded from below by 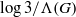 $\log 3/ \Lambda (G)$, where
$\log 3/ \Lambda (G)$, where 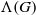 $\Lambda (G)$ is a constant depending on the combinatorial structure of
$\Lambda (G)$ is a constant depending on the combinatorial structure of 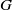 $G$. The exact value of the infimum on
$G$. The exact value of the infimum on 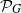 ${ \mathcal{P} }_{G} $ is calculated for some families of graphs. The main tool is a refined version of the structure theorem for mixing graph maps. It also yields new proofs of some known results, including Blokh’s theorem (topological mixing implies the specification property for maps on graphs).
${ \mathcal{P} }_{G} $ is calculated for some families of graphs. The main tool is a refined version of the structure theorem for mixing graph maps. It also yields new proofs of some known results, including Blokh’s theorem (topological mixing implies the specification property for maps on graphs).