No CrossRef data available.
Published online by Cambridge University Press: 04 June 2014
Let  $A$ be a finite alphabet and
$A$ be a finite alphabet and 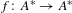 $f:~A^{\ast }\rightarrow A^{\ast }$ be a morphism with an iterative fixed point
$f:~A^{\ast }\rightarrow A^{\ast }$ be a morphism with an iterative fixed point 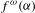 $f^{{\it\omega}}({\it\alpha})$, where
$f^{{\it\omega}}({\it\alpha})$, where 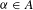 ${\it\alpha}\in A$. Consider the subshift
${\it\alpha}\in A$. Consider the subshift 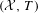 $({\mathcal{X}},T)$, where
$({\mathcal{X}},T)$, where 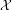 ${\mathcal{X}}$ is the shift orbit closure of
${\mathcal{X}}$ is the shift orbit closure of 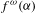 $f^{{\it\omega}}({\it\alpha})$ and
$f^{{\it\omega}}({\it\alpha})$ and 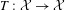 $T:~{\mathcal{X}}\rightarrow {\mathcal{X}}$ is the shift map. Let
$T:~{\mathcal{X}}\rightarrow {\mathcal{X}}$ is the shift map. Let  $S$ be a finite alphabet that is in bijective correspondence via a mapping
$S$ be a finite alphabet that is in bijective correspondence via a mapping  $c$ with the set of non-empty suffixes of the images
$c$ with the set of non-empty suffixes of the images 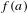 $f(a)$ for
$f(a)$ for 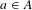 $a\in A$. Let
$a\in A$. Let 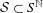 ${\mathcal{S}}\subset S^{\mathbb{N}}$ be the set of infinite words
${\mathcal{S}}\subset S^{\mathbb{N}}$ be the set of infinite words 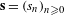 $\mathbf{s}=(s_{n})_{n\geq 0}$ such that
$\mathbf{s}=(s_{n})_{n\geq 0}$ such that 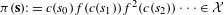 ${\it\pi}(\mathbf{s}):=c(s_{0})f(c(s_{1}))f^{2}(c(s_{2}))\cdots \in {\mathcal{X}}$. We show that if
${\it\pi}(\mathbf{s}):=c(s_{0})f(c(s_{1}))f^{2}(c(s_{2}))\cdots \in {\mathcal{X}}$. We show that if 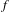 $f$ is primitive,
$f$ is primitive, 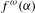 $f^{{\it\omega}}({\it\alpha})$ is aperiodic, and
$f^{{\it\omega}}({\it\alpha})$ is aperiodic, and 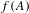 $f(A)$ is a suffix code, then there exists a mapping
$f(A)$ is a suffix code, then there exists a mapping 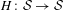 $H:~{\mathcal{S}}\rightarrow {\mathcal{S}}$ such that
$H:~{\mathcal{S}}\rightarrow {\mathcal{S}}$ such that 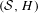 $({\mathcal{S}},H)$ is a topological dynamical system and
$({\mathcal{S}},H)$ is a topological dynamical system and 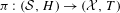 ${\it\pi}:~({\mathcal{S}},H)\rightarrow ({\mathcal{X}},T)$ is a conjugacy; we call
${\it\pi}:~({\mathcal{S}},H)\rightarrow ({\mathcal{X}},T)$ is a conjugacy; we call 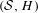 $({\mathcal{S}},H)$ the suffix conjugate of
$({\mathcal{S}},H)$ the suffix conjugate of 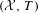 $({\mathcal{X}},T)$. In the special case where
$({\mathcal{X}},T)$. In the special case where 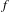 $f$ is the Fibonacci or Thue–Morse morphism, we show that the subshift
$f$ is the Fibonacci or Thue–Morse morphism, we show that the subshift 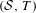 $({\mathcal{S}},T)$ is sofic, that is, the language of
$({\mathcal{S}},T)$ is sofic, that is, the language of 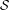 ${\mathcal{S}}$ is regular.
${\mathcal{S}}$ is regular.