Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T21:48:10.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Schmidt games and non-dense forward orbits of certain partially hyperbolic systems

Published online by Cambridge University Press:  11 February 2015

WEISHENG WU
WEISHENG WU*
Affiliation:
Department of Mathematics, Pennsylvania State University, University Park, PA 16802, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 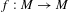$f:M\rightarrow M$ be a partially hyperbolic diffeomorphism with conformality on unstable manifolds. Consider a set of points with non-dense forward orbit: 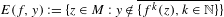$E(f,y):=\{z\in M:y\notin \overline{\{f^{k}(z),k\in \mathbb{N}\}}\}$ for some 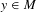$y\in M$. Define 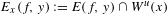$E_{x}(f,y):=E(f,y)\cap W^{u}(x)$ for any 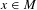$x\in M$. Following a method of Broderick, Fishman and Kleinbock [Schmidt’s game, fractals, and orbits of toral endomorphisms. Ergod. Th. & Dynam. Sys.31 (2011), 1095–1107], we show that 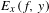$E_{x}(f,y)$ is a winning set for Schmidt games played on 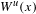$W^{u}(x)$ which implies that 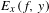$E_{x}(f,y)$ has Hausdorff dimension equal to 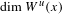$\dim W^{u}(x)$. Furthermore, we show that for any non-empty open set 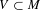$V\subset M$, 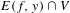$E(f,y)\cap V$ has full Hausdorff dimension equal to 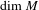$\dim M$, by constructing measures supported on 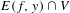$E(f,y)\cap V$ with lower pointwise dimension converging to 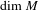$\dim M$ and with conditional measures supported on 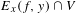$E_{x}(f,y)\cap V$. The results can be extended to the set of points with forward orbit staying away from a countable subset of 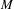$M$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 5 , August 2016 , pp. 1656 - 1678
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aravinda, C. S. and Leuzinger, E.. Bounded geodesics in rank-1 locally symmetric spaces. Ergod. Th. & Dynam. Sys. 15(5) (1995), 813–820.Google Scholar
Brin, M. and Pesin, Ja. B.. Partially hyperbolic dynamical systems. Math. USSR-Izv. 8(1) (1974), 117–218.Google Scholar
Broderick, R., Fishman, L. and Kleinbock, D. Y.. Schmidt’s game, fractals, and orbits of toral endomorphisms. Ergod. Th. & Dynam. Sys. 31 (2011), 1095–1107.Google Scholar
Burns, K. and Wilkinson, A.. On the ergodicity of partially hyperbolic systems. Ann. of Math. (2) 171 (2010), 451–489.CrossRefGoogle Scholar
Dani, S. G.. Divergent trajectories of flows on homogeneous spaces and Diophantine approximation. J. Reine Angew. Math. 359 (1985), 55–89, 102.Google Scholar
Dani, S. G.. Bounded orbits of flows on homogeneous spaces. Comment. Math. Helv. 61(1) (1986), 636–660.Google Scholar
Dani, S. G.. On orbits of endomorphisms of tori and the Schmidt game. Ergod. Th. & Dynam. Sys. 8(4) (1988), 523–529.Google Scholar
Dani, S. G. and Shah, H.. Badly approximable numbers and vectors in Cantor-like sets. Proc. Amer. Math. Soc. 140(8) (2012), 2575–2587.Google Scholar
Dolgopyat, D.. Bounded orbits of Anosov flows. Duke Math. J. 87(1) (1997), 87–114.Google Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications. Wiley, Chichester, 2003.Google Scholar
Fishman, L., Simmons, D. S. and Urbański, M.. Diophantine approximation and the geometry of limit sets in Gromov hyperbolic metric spaces (extended version). Preprint, 2013, arXiv:1301.5630.Google Scholar
Franks, J. M.. Invariant sets of hyperbolic toral automorphisms. Amer. J. Math. 99(5) (1977), 1089–1095.Google Scholar
Hertz, F. R., Hertz, M. A. R. and Ures, R.. Accessibility and stable ergodicity for partially hyperbolic diffeomorphisms with 1d-center bundle. Invent. Math. 172(2) (2008), 353–381.Google Scholar
Katok, A.. Nonuniform Hyperbolicity and Structure of Smooth Dynamical Systems (Proc. Int. Congress Math., Vol. 2, Warszawa, 1983). Polish Scientific Publishers PWN, Warsaw, 1984, pp. 1245–1254.Google Scholar
Katok, A. and Mendoza, L.. Dynamical systems with non-uniformly hyperbolic behavior. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995, pp. 659–700.CrossRefGoogle Scholar
Kleinbock, D. Y. and Margulis, G. A.. Bounded orbits of non-quasiunipotent flows on homogeneous spaces. Amer. Math. Soc. Transl. 171 (1996), 141–172.Google Scholar
Kleinbock, D. Y. and Weiss, B.. Modified Schmidt games and Diophantine approximation with weights. Adv. Math. 223(4) (2010), 1276–1298.Google Scholar
Kleinbock, D. Y. and Weiss, B.. Modified Schmidt games and a conjecture of Margulis. Preprint, 2010,arXiv:1001.5017.Google Scholar
Mañé, R.. Orbits of paths under hyperbolic toral automorphisms. Proc. Amer. Math. Soc. 73(1) (1979), 121–125.Google Scholar
McMullen, C.. Area and Hausdorff dimension of Julia sets of entire functions. Trans. Amer. Math. Soc. 300(1) (1987), 329–342.Google Scholar
Przytycki, F.. Construction of invariant sets for Anosov diffeomorphisms and hyperbolic attractors. Studia Math. 68(2) (1980), 199–213.Google Scholar
Pugh, C. and Shub, M.. Ergodicity of Anosov actions. Invent. Math. 15(1) (1972), 1–23.CrossRefGoogle Scholar
Quas, A. and Soo, T.. Ergodic universality of some topological dynamical systems. Preprint, 2012,arXiv:1208.3501.Google Scholar
Schmidt, W. M.. On badly approximable numbers and certain games. Trans. Amer. Math. Soc. 123(1) (1966), 178–199.CrossRefGoogle Scholar
Schmidt, W. M.. Badly approximable systems of linear forms. J. Number Theory 1(2) (1969), 139–154.Google Scholar
Sun, P.. Zero-entropy invariant measures for skew product diffeomorphisms. Ergod. Th. & Dynam. Sys. 30(3) (2010), 923–930.Google Scholar
Sun, P.. Measures of intermediate entropies for skew product diffeomorphisms. Discrete Contin. Dyn. Syst. 27 (2010), 1219–1231.Google Scholar
Sun, P.. Density of metric entropies for linear toral automorphisms. Dyn. Syst. 27(2) (2012), 197–204.Google Scholar
Urbański, M.. The Hausdorff dimension of the set of points with non-dense orbit under a hyperbolic dynamical system. Nonlinearity 4(2) (1991), 385–397.Google Scholar